Analysis of Lie Symmetries with Conservation Laws and Solutions of Generalized (4 + 1)-Dimensional Time-Fractional Fokas Equation
Abstract
:1. Introduction
2. Derivation of (4 + 1)-Dimensional Time Fraction Fokas Equation
3. Conservation Laws and Lie Symmetry Analysis of (4 + 1)-Dimensional Time-Fractional Order Fokas Equations
3.1. Lie Symmetry Analysis
3.2. Conservation Laws
4. The Exact Solutions of the Time-Fractional Fokas Equation
4.1. Rogue Wave Solutions of the (4 + 1)-Dimensional Time-Fractional Fokas Equation
4.2. Multiple Soliton Solutions of the (4 + 1)-Dimensional Time-Fractional Fokas Equation
5. The Numerical Solutions of the Time-Fractional Fokas Equation
5.1. Time Discretization
5.2. Radial Basis Function Meshless Method
5.3. Discussion of the Solutions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benkhettou, N.; Hassani, S.; Torres, D.F.M. A conformable fractional calculus on arbitrary time scales. J. King Saud Univ. Sci. 2016, 28, 93–98. [Google Scholar] [CrossRef]
- Lokenath, D. Recent applications of fractional calculus to science and engineering. Int. J. Math. Math. Sci. 2014, 2003, 3413–3442. [Google Scholar]
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Order. Mathematics 2008, 49, 277–290. [Google Scholar]
- Miller, K.S.; Ross, B. An introduction to the fractional calculus and fractional differential equations. Wiley 1993, 126–174. [Google Scholar]
- Agarwal, R.P.; Benchohra, M.; Hamani, S. A Survey on Existence Results for Boundary Value Problems of Nonlinear Fractional Differential Equations and Inclusions. Acta Appl. Math. 2010, 109, 973–1033. [Google Scholar] [CrossRef]
- Sakar, M.G.; Uludag, F.; Erdogan, F. Numerical solution of time-fractional nonlinear PDEs with proportional delays by homotopy perturbation method. Appl. Math. Model. 2016, 40, 6639–6649. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Asgari, Z. Solution of stochastic nonlinear time fractional PDEs using polynomial chaos expansion combined with an exponential integrator. Comput. Math. Appl. 2016, 73, 997–1007. [Google Scholar] [CrossRef]
- Hosseini, K.; Ma, W.X.; Ansari, R.; Mirzazadeh, M.; Pouyanmehr, R.; Samadani, F. Evolutionary behavior of rational wave solutions to the (4 + 1)- dimensional Boiti-Leon-Manna-Pempinelli equation. Phys. Scr. 2020, 95, 065208. [Google Scholar] [CrossRef]
- Fokas, A.S. Integrable nonlinear evolution partial differential equations in 4 + 2 and 3 + 1 dimensions. Phys. Rev. Lett. 2006, 96, 190201. [Google Scholar] [CrossRef]
- Ohta, Y.; Yang, J. Rogue waves in the Davey-Stewartson I equation. Phys. Rev. E Stat. Nonlin. Soft Matter. Phys. 2012, 86, 694–698. [Google Scholar] [CrossRef] [Green Version]
- Jafari, H.; Kadem, A.; Baleanu, D.; Yilmaz, T. Solutions of the fractional Davey-Stewartson equations with variational iteration method. Rom. Rep. Phys. 2012, 64, 337–346. [Google Scholar]
- Ying, Z.; Xie, F.; Lv, Z. Symbolic computation in non-linear evolution equation: Application to (3 + 1)-dimensional Kadomtsev-Petviashvili equation. Chaos Solitons Fractals 2005, 24, 257–263. [Google Scholar]
- Bi, Y.; Zhang, Z.; Liu, Q.; Liu, T. Research on nonlinear waves of blood flflow in arterial vessels. Commun. Nonlinear Sci. Numer. Simul. 2021, 102, 105918. [Google Scholar] [CrossRef]
- Yang, Y.; Song, J. On the generalized eigenvalue problem of Rossby waves vertical velocity under the condition of zonal mean flow and topography. Appl. Math. Lett. 2021, 121, 107485. [Google Scholar] [CrossRef]
- El-Ganaini, S.; Al-Amr, M.O. New abundant wave solutions of the conformable space-time fractional (4 + 1)-dimensional Fokas equation in water waves. Comput. Math. Appl. 2019, 78, 2094–2106. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, H. Fractional sub-equation method and its applications to nonlinear fractional PDEs. Phys. Lett. A 2011, 375, 1069–1073. [Google Scholar] [CrossRef]
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals 2005, 26, 695–700. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function method for nonlinear wave equations. Chaos Solitons Fractals 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Ramos, J.I. On the variational iteration method and other iterative techniques for nonlinear differential equations. Appl. Math. Comput. 2008, 199, 39–69. [Google Scholar] [CrossRef]
- Demiray, S.T.; Bulut, H. A New Method for (4 + 1)-Dimensional Fokas Equation. ITM Web Conf. 2008, 22, 01065. [Google Scholar] [CrossRef]
- He, Y. Exact Solutions for-Dimensional Nonlinear Fokas Equation Using Extended F-Expansion Method and Its Variant. Math. Probl. Eng. 2014, 2014, 972519. [Google Scholar]
- Lee, J.; Sakthivel, R.; Wazzan, L. Exact travelling wave solutions of a higher-dimensions of a higher-dimensional nonlinear evolution equation. Mod. Phys. Lett. B 2010, 24, 1011–1021. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Multiple-soliton solutions for the KP equation by Hirota’s bilinear method and by the tanh-coth method. Appl. Math. Comput. 2007, 190, 633–640. [Google Scholar] [CrossRef]
- Tian, H.F.; Ha, J.T.; Zhang, H.Q. Lump-type solutions, interaction solutions and periodic wave solutions of a (3 + 1)-dimensional Korteweg-de Vries equation. Int. J. Mod. Phys. B 2019, 33, 1950319. [Google Scholar] [CrossRef]
- Tajiri, M.; Takeuchi, K.; Arai, T. Soliton Stability to the Davey-Stewartson I Equation by the Hirota Method. J. Phys. Soc. Jpn. 2001, 70, 1505–1511. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, D. Multisoliton solutions of a (2 + 1)-dimensional variable-coefficient Toda lattice equation via Hirota’s bilinear method. Can. J. Phys. 2014, 92, 184–190. [Google Scholar] [CrossRef]
- Dong, M.J.; Tian, S.F.; Yan, X.W.; Zou, L. Solitary waves, homoclinic breather waves and rogue waves of the (3 + 1)-dimensional Hirota bilinear equation. Comput. Math. Appl. 2018, 75, 957–964. [Google Scholar] [CrossRef]
- Feng, B.F. General N-soliton solution to a vector nonlinear Schrödinger equation. J. Phys. A Math. Theor. 2014, 47, 355203. [Google Scholar] [CrossRef]
- Wang, D.S.; Zhang, Y.; Dong, H.H. Riemann-Hilbert problems and soliton solutions for a multi-component cubic-quintic nonlinear Schrödinger equation. J. Geom. Phys. 2020, 149, 103569. [Google Scholar]
- Ohta, Y.; Yang, J. General high-order rogue waves and their dynamics in the nonlinear Schrodinger equation. Proc. R. Soc. Math. Phys. Eng. Sci. 2012, 468, 1716–1740. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.H.; Porsezian, K.; He, J.S. Breather and rogue wave solutions of a generalized nonlinear Schrödinger equation. Phys. Rev. E 2013, 87, 053202. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lv, Z.S.; Zhang, H.Q. Soliton-like and period form solutions for high dimensional nonlinear evolution equations. Solitons Fractals 2003, 17, 669–673. [Google Scholar]
- Zhu, X.G.; Nie, Y.F.; Wang, J.G.; Yuan, Z.B. An advanced meshless approach for the high-dimensional multi-term time-space-fractional PDEs on convex domains. Nonlinear Dyn. 2021, 104, 1555–1580. [Google Scholar] [CrossRef]
- Chenoweth, M.E. A Local Radial Basis Function Method for the Numerical Solution of Partial Differential Equations. Master’s Thesis, Marshall University, Huntington, WV, USA, 2012. [Google Scholar]
- Khalique, C.M.; Adem, A.R. Symmetry reductions, exact solutions and conservation laws of a new coupled KdV system. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3465–3475. [Google Scholar]
- Leo, R.A.; Sicuro, G.; Tempesta, P. A foundational approach to the Lie theory for fractional order partial differential equations. Fract. Calc. Appl. Anal. 2017, 20, 212. [Google Scholar] [CrossRef] [Green Version]
- Kinani, E.E.; Ouhadan, A. Lie symmetry analysis of some time fractional partial differential equations. Int. J. Mod. Phys. Conf. 2015, 38, 1560075. [Google Scholar] [CrossRef] [Green Version]
- Treanţă, S. Gradient Structures Associated with a Polynomial Differential Equation. Mathematics 2020, 8, 535. [Google Scholar] [CrossRef] [Green Version]
- Lie, S. Theorie der Transformationsgruppen I. Christiania 1880, 16, 441–528. [Google Scholar] [CrossRef]
- Sun, J.C.; Zhang, Z.G.; Dong, H.H.; Yang, H.W. Dust acoustic rogue waves of fractional-order model in dusty plasma. Commun. Theor. Phys. 2020, 72, 17. [Google Scholar] [CrossRef]
- Gazizov, R.K.; Kasatkin, A.A.; Lukashchuk, S.Y. Continuous transformation groups of fractional differential equations. Vestn. Usatu 2007, 9, 21. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, J. Advances in Fractional Calculus. Fract. Var. Princ. 2007, 115–126. [Google Scholar]
- He, J.H.; Wu, G.C.; Austin, F. The Variational Iteration Method Which Should Be Followed. Nonl. Sci. Lett. A 2010, 1, 1–30. [Google Scholar]
- Saxena, R.; Mathai, A.; Haubold, H. Space-time fractional reaction-diffusion equations associated with a generalized Riemann-Liouville fractional derivative. Axioms 2014, 3, 320–334. [Google Scholar] [CrossRef] [Green Version]
- Treanţă, S. Noether-Type First Integrals Associated with Autonomous Second-Order Lagrangians. Symmetru 2019, 11, 1088. [Google Scholar] [CrossRef] [Green Version]
- He, J.H. A tutorial and heuristic review on Lagrange multiplier for optimal problems. Nonlinear Sci. Lett. A 2017, 8, 121–148. [Google Scholar]
- Hu, J.; Ye, Y.; Shen, S.; Zhang, J. Lie symmetry analysis of the time fractional KdV-type equation. Appl. Math. Comput. 2014, 233, 439–444. [Google Scholar] [CrossRef]
- Saberi, E.; Hejazi, S.R. Lie symmetry analysis, conservation laws and exact solutions of the time-fractional generalized Hirota-Satsuma coupled KdV system. Phys. A Stat. Mech. Its Appl. 2018, 492, 296–307. [Google Scholar] [CrossRef]
- Agarwal, P.; Tariboon, J.; Ntouyas, S.K. Some generalized Riemann-Liouville k-fractional integral inequalities. J. Inequalities Appl. 2016, 2016, 122. [Google Scholar] [CrossRef] [Green Version]
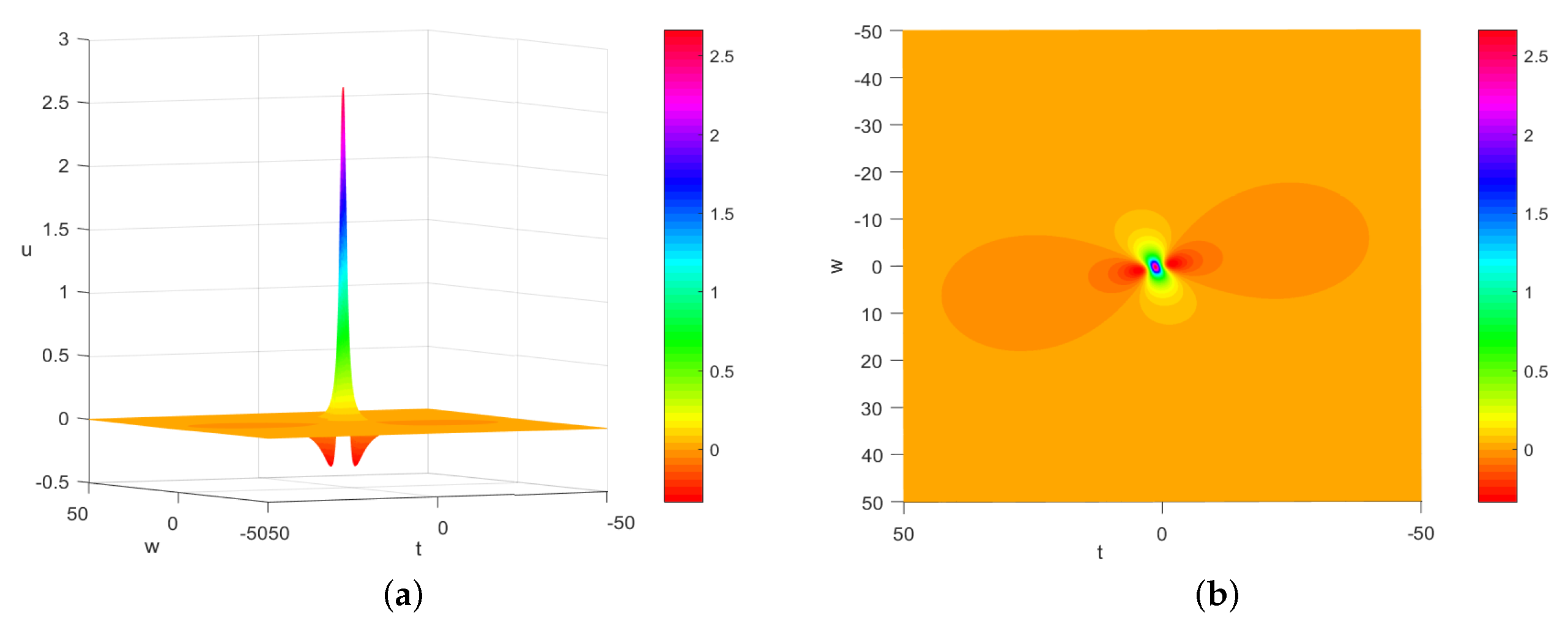
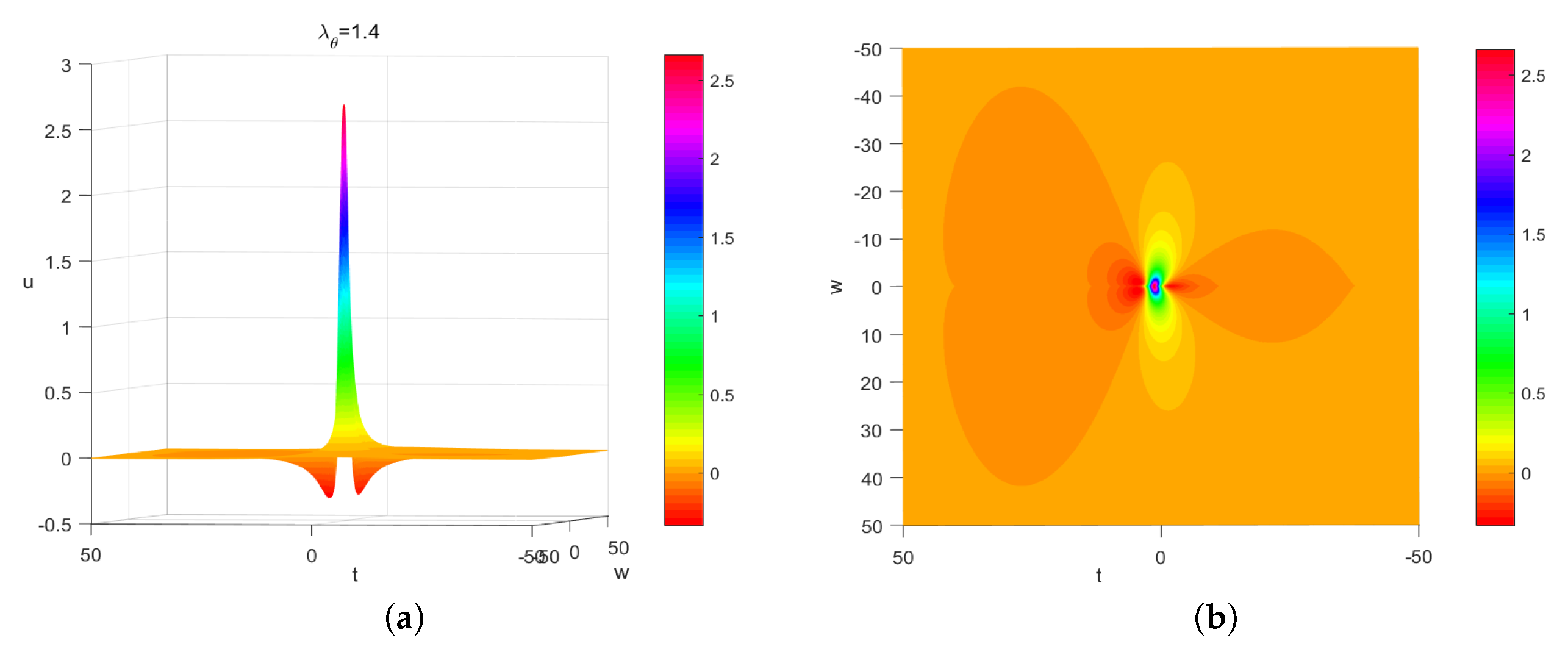
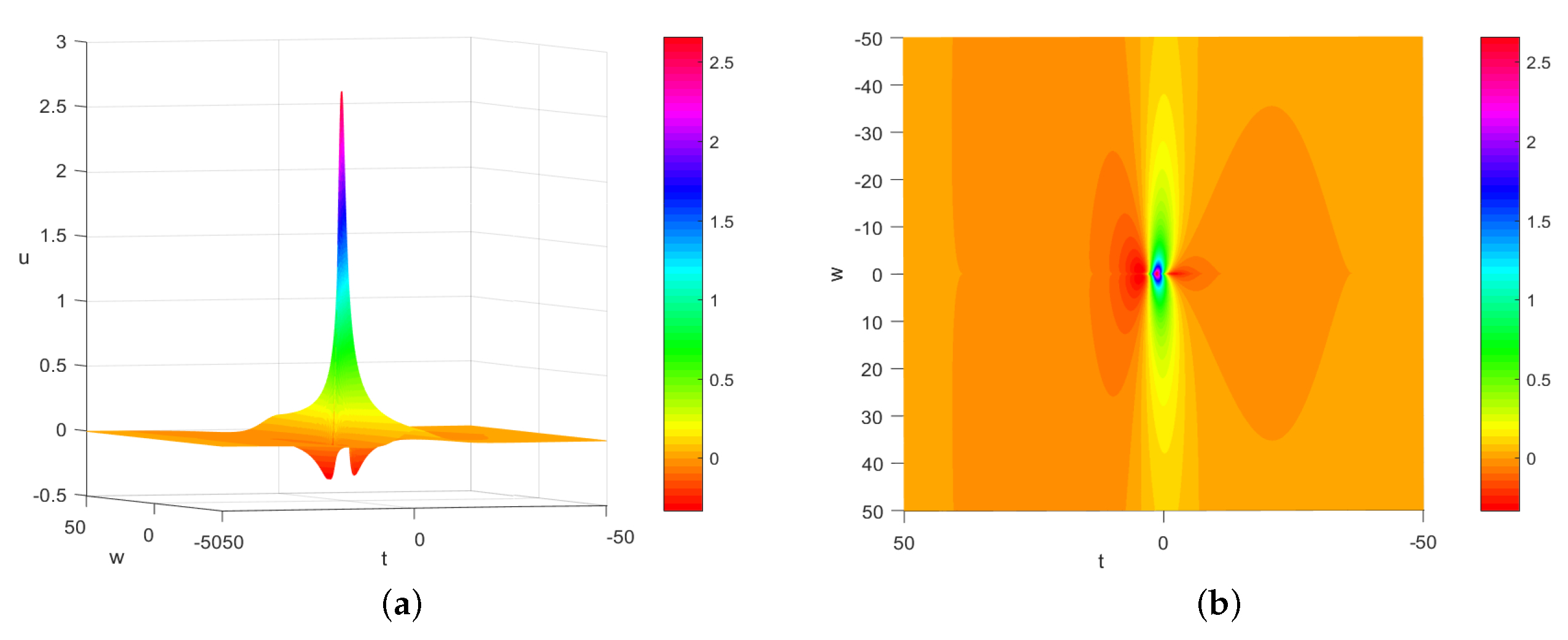

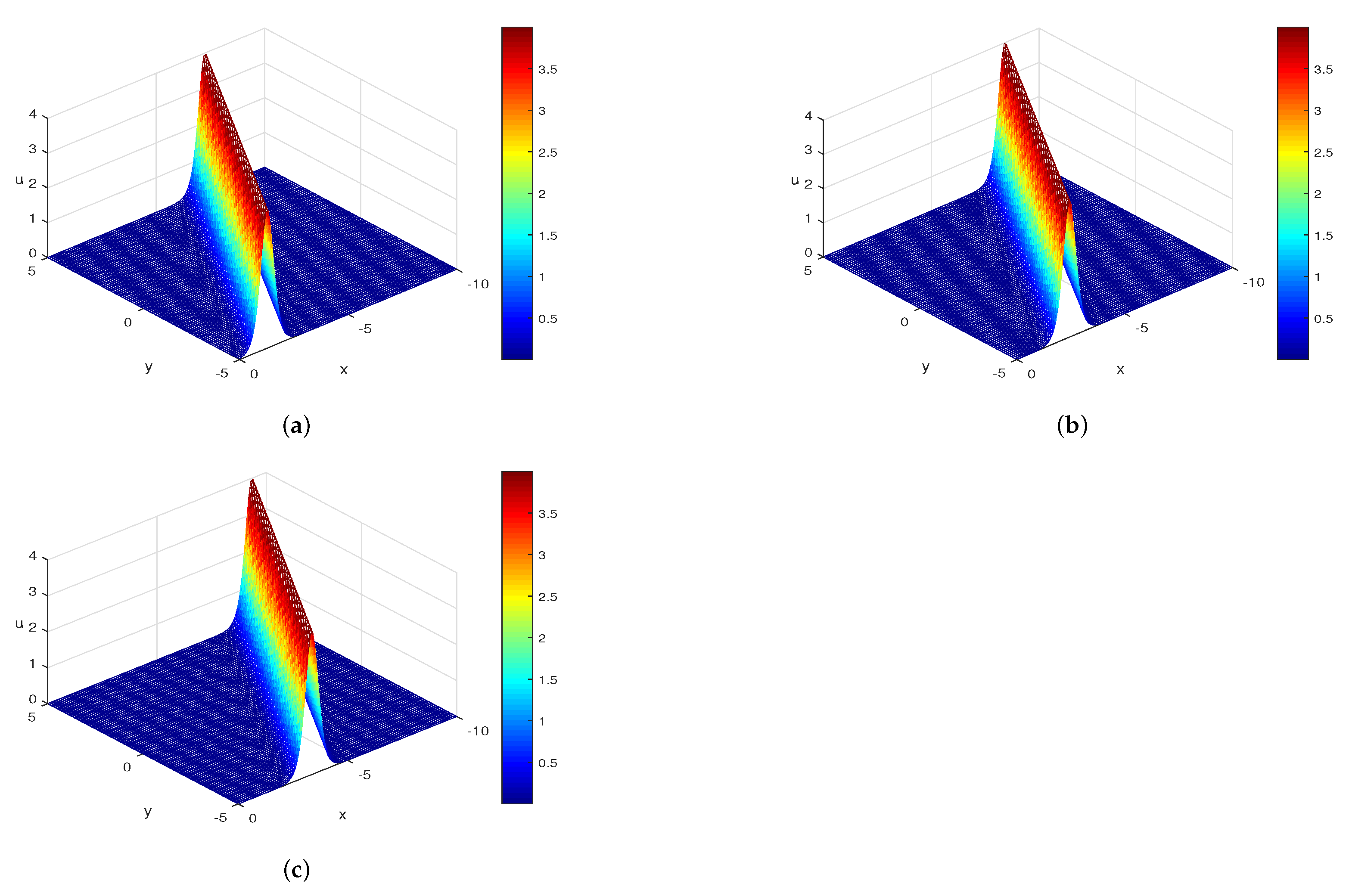
| t = 0.1 | t = 0.2 | t = 0.3 | t = 0.4 | t = 0.5 | t = 0.6 | t = 0.7 | t = 0.8 | t = 0.9 | t = 1 | |
| 0.1 | 4.17 | 1.11 | 1.51 | 1.63 | 1.50 | 1.16 | 6.65 | 1.01 | 4.48 | 8.95 |
| 0.2 | 1.75 | 6.93 | 1.06 | 1.28 | 1.40 | 1.43 | 1.40 | 1.34 | 1.31 | 1.34 |
| 0.3 | 6.50 | 3.07 | 4.53 | 5.37 | 5.96 | 6.65 | 7.81 | 9.78 | 1.29 | 1.73 |
| 0.4 | 9.50 | 1.60 | 1.51 | 1.03 | 5.13 | 3.65 | 1.01 | 2.87 | 6.36 | 1.18 |
| 0.5 | 8.60 | 1.04 | 5.83 | 2.44 | 1.17 | 1.87 | 1.97 | 1.02 | 1.43 | 5.82 |
| 0.6 | 7.40 | 2.19 | 2.16 | 3.05 | 5.74 | 1.21 | 1.65 | 1.50 | 3.06 | 2.43 |
| 0.7 | 4.22 | 2.15 | 6.35 | 2.96 | 6.49 | 5.06 | 6.45 | 3.41 | 2.63 | 8.12 |
| 0.8 | 9.53 | 5.73 | 2.57 | 1.99 | 1.24 | 1.74 | 1.41 | 5.46 | 4.00 | 8.87 |
| 0.9 | 1.64 | 1.08 | 5.92 | 2.13 | 3.29 | 1.36 | 1.05 | 3.39 | 2.33 | 4.34 |
| 1 | 2.47 | 1.73 | 1.09 | 5.93 | 2.70 | 1.38 | 1.91 | 3.99 | 7.14 | 1.07 |
| t = 0.1 | t = 0.2 | t = 0.3 | t = 0.4 | t = 0.5 | t = 0.6 | t = 0.7 | t = 0.8 | t = 0.9 | t = 1 | |
| 0.1 | 2.18 | 1.49 | 9.79 | 6.20 | 3.85 | 2.42 | 1.58 | 9.66 | 2.37 | 9.43 |
| 0.2 | 1.86 | 1.58 | 1.43 | 1.37 | 1.36 | 1.34 | 1.26 | 1.08 | 7.54 | 2.57 |
| 0.3 | 1.13 | 1.09 | 1.16 | 1.30 | 1.47 | 1.62 | 1.68 | 1.62 | 1.38 | 9.23 |
| 0.4 | 5.37 | 5.94 | 7.44 | 9.52 | 1.18 | 1.39 | 1.53 | 1.57 | 1.44 | 1.11 |
| 0.5 | 2.39 | 2.87 | 4.09 | 5.80 | 7.76 | 9.67 | 1.12 | 1.19 | 1.14 | 9.27 |
| 0.6 | 2.43 | 2.03 | 2.24 | 2.92 | 3.97 | 5.21 | 6.39 | 7.21 | 7.27 | 6.14 |
| 0.7 | 5.06 | 3.26 | 1.99 | 1.29 | 1.15 | 1.54 | 2.28 | 3.13 | 3.70 | 3.56 |
| 0.8 | 9.69 | 6.19 | 3.26 | 1.07 | 2.57 | 6.74 | 2.66 | 7.30 | 1.94 | 2.89 |
| 0.9 | 1.57 | 1.05 | 5.93 | 2.36 | 2.56 | 9.63 | 6.49 | 7.35 | 2.79 | 5.00 |
| 1 | 2.28 | 1.59 | 9.90 | 5.24 | 2.21 | 9.84 | 1.52 | 3.58 | 6.72 | 1.03 |
| t = 0.1 | t = 0.2 | t = 0.3 | t = 0.4 | t = 0.5 | t = 0.6 | t = 0.7 | t = 0.8 | t = 0.9 | t = 1 | |
| 0.1 | 3.86 | 8.85 | 1.09 | 1.05 | 8.04 | 4.48 | 9.08 | 1.42 | 1.21 | 2.78 |
| 0.2 | 5.36 | 9.70 | 1.19 | 1.22 | 1.08 | 8.30 | 5.52 | 3.47 | 3.30 | 6.20 |
| 0.3 | 2.75 | 5.40 | 6.82 | 7.22 | 6.87 | 6.16 | 5.62 | 5.95 | 7.94 | 1.25 |
| 0.4 | 8.43 | 1.70 | 1.75 | 1.31 | 7.59 | 5.24 | 1.14 | 3.20 | 7.35 | 1.42 |
| 0.5 | 6.02 | 6.82 | 1.13 | 1.16 | 2.40 | 3.22 | 3.05 | 1.18 | 3.11 | 1.05 |
| 0.6 | 4.23 | 1.16 | 9.64 | 5.15 | 1.30 | 2.66 | 3.44 | 2.90 | 2.03 | 5.49 |
| 0.7 | 2.00 | 6.26 | 2.12 | 2.52 | 1.96 | 7.32 | 6.44 | 1.45 | 8.14 | 2.21 |
| 0.8 | 8.74 | 3.40 | 5.72 | 3.05 | 4.00 | 3.59 | 2.21 | 5.28 | 5.84 | 1.40 |
| 0.9 | 2.14 | 1.30 | 6.14 | 1.22 | 1.62 | 2.41 | 1.46 | 6.12 | 2.97 | 4.60 |
| 1 | 4.11 | 2.96 | 1.99 | 1.25 | 7.76 | 5.65 | 5.94 | 8.10 | 1.13 | 1.44 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z.; Zhang, Z.-G.; Li, J.-J.; Yang, H.-W. Analysis of Lie Symmetries with Conservation Laws and Solutions of Generalized (4 + 1)-Dimensional Time-Fractional Fokas Equation. Fractal Fract. 2022, 6, 108. https://doi.org/10.3390/fractalfract6020108
Jiang Z, Zhang Z-G, Li J-J, Yang H-W. Analysis of Lie Symmetries with Conservation Laws and Solutions of Generalized (4 + 1)-Dimensional Time-Fractional Fokas Equation. Fractal and Fractional. 2022; 6(2):108. https://doi.org/10.3390/fractalfract6020108
Chicago/Turabian StyleJiang, Zhuo, Zong-Guo Zhang, Jing-Jing Li, and Hong-Wei Yang. 2022. "Analysis of Lie Symmetries with Conservation Laws and Solutions of Generalized (4 + 1)-Dimensional Time-Fractional Fokas Equation" Fractal and Fractional 6, no. 2: 108. https://doi.org/10.3390/fractalfract6020108





