A Novel Modeling Method of Micro-Topography for Grinding Surface Based on Ubiquitiform Theory
Abstract
:1. Introduction
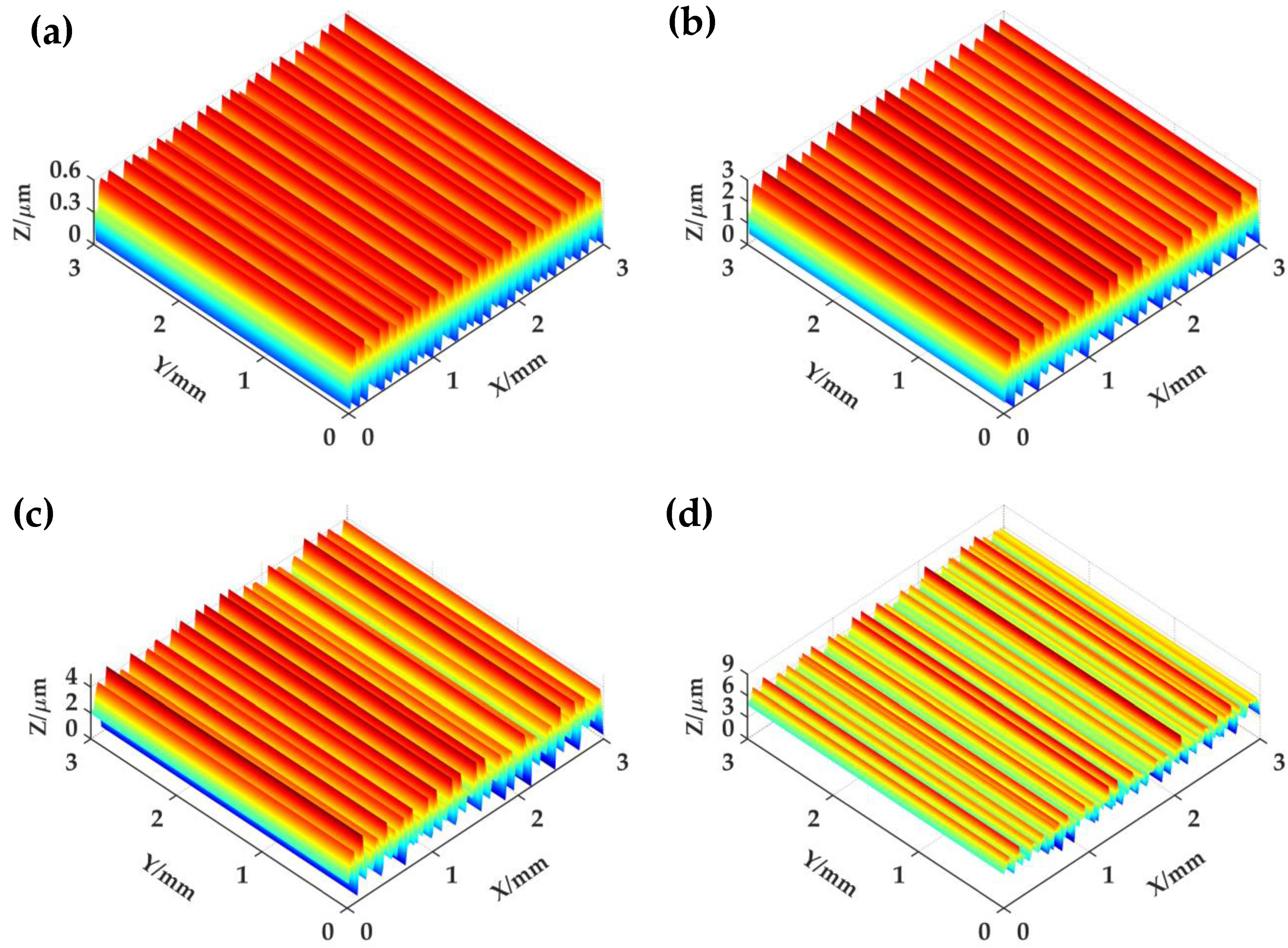
2. Characteristic Analysis of Measured Surfaces
3. Modeling Method
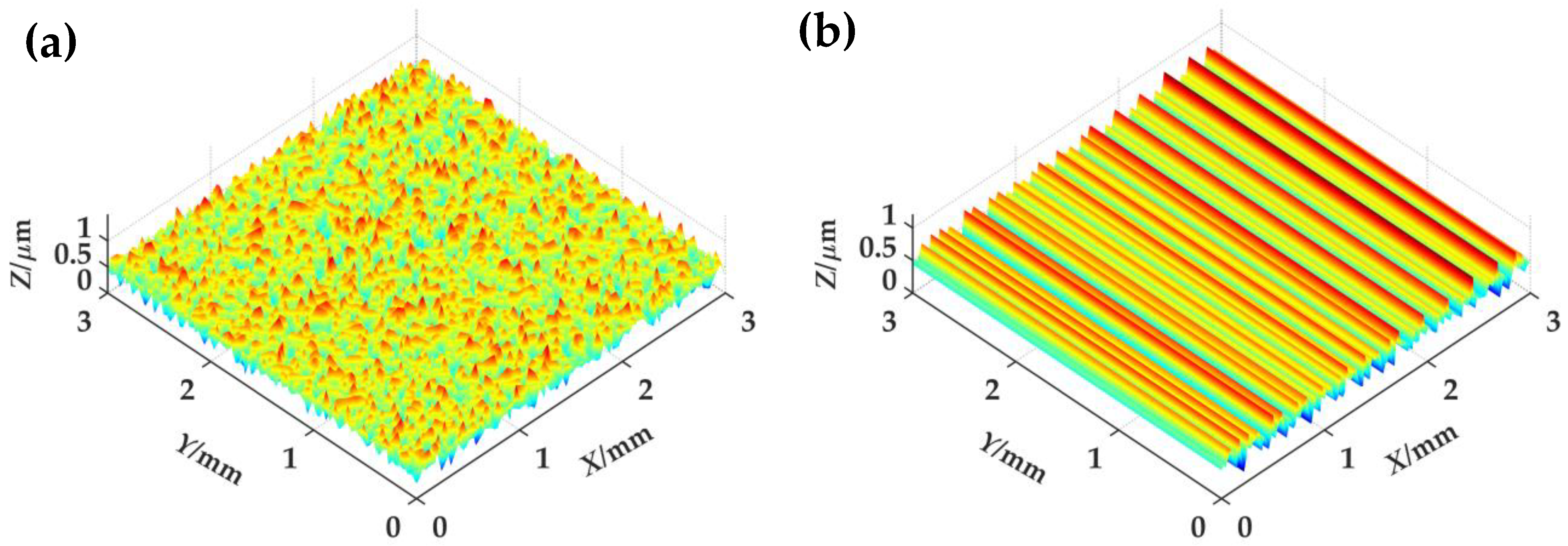
3.1. Modeling Method Based on Fractal Theory
3.2. Modeling Method Based on Ubiquitiform Theory
4. Modeling of Grinding Surface
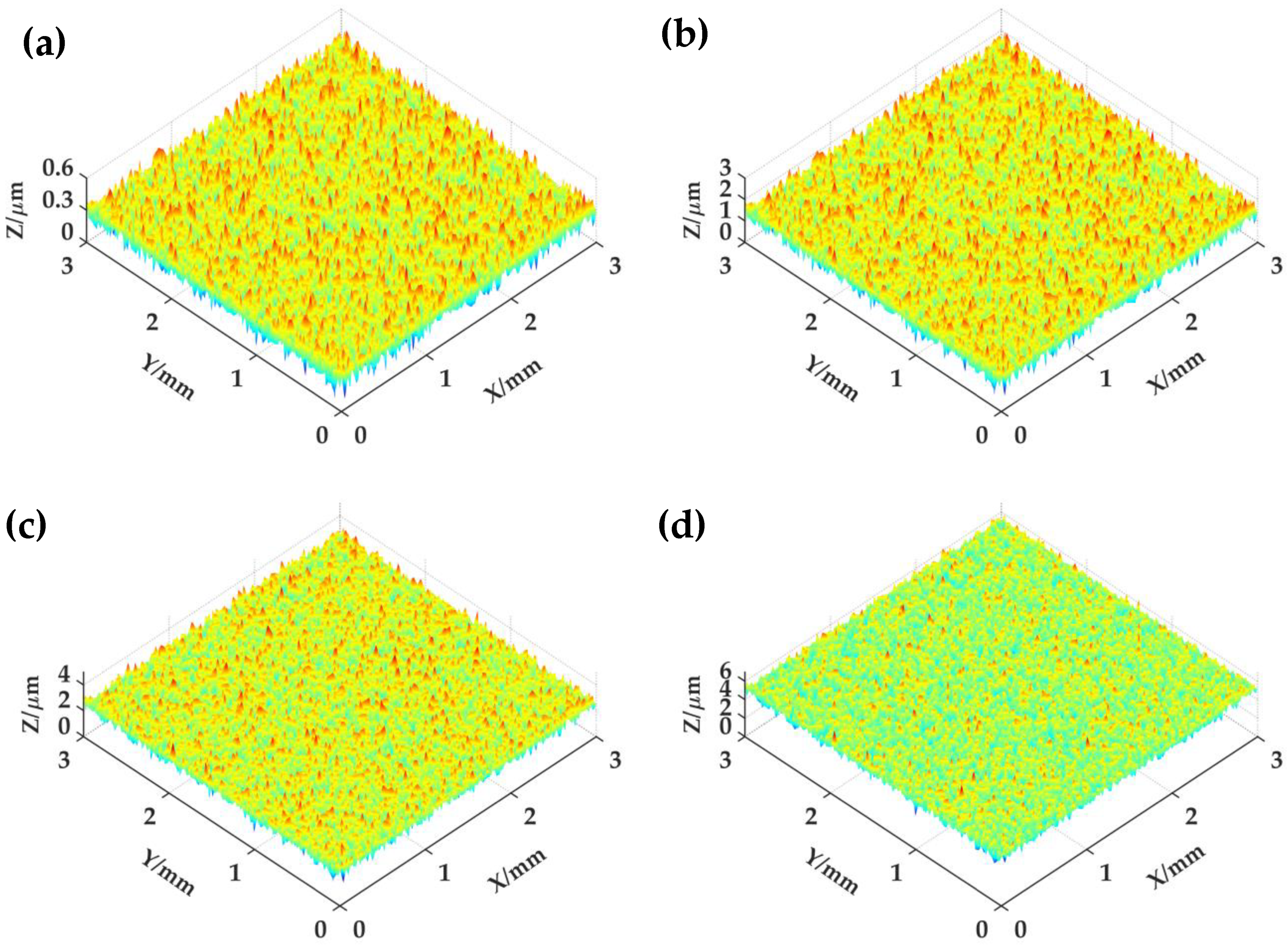
5. Results Comparison
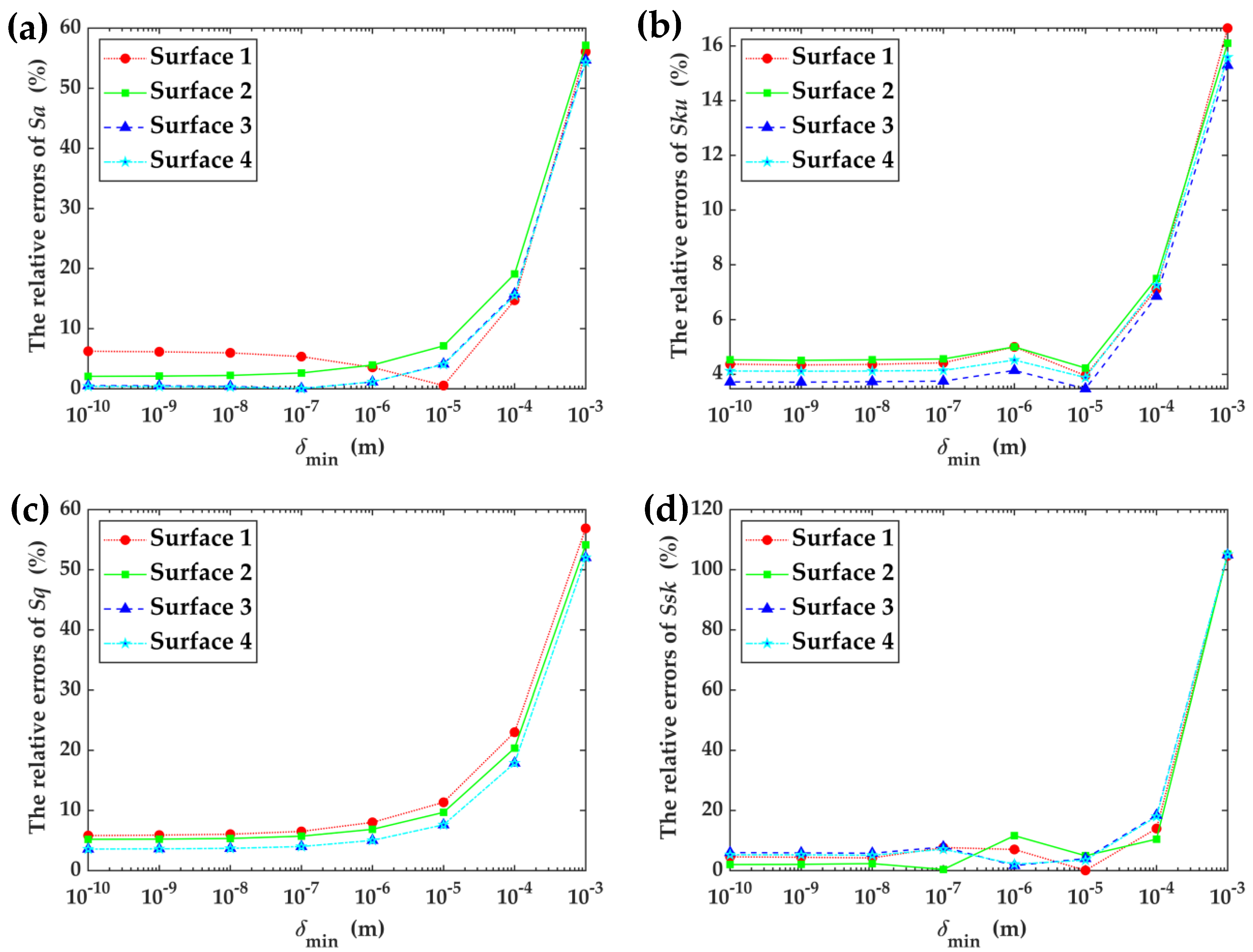
5.1. Different Lower Bound to Scale Invariance δmin
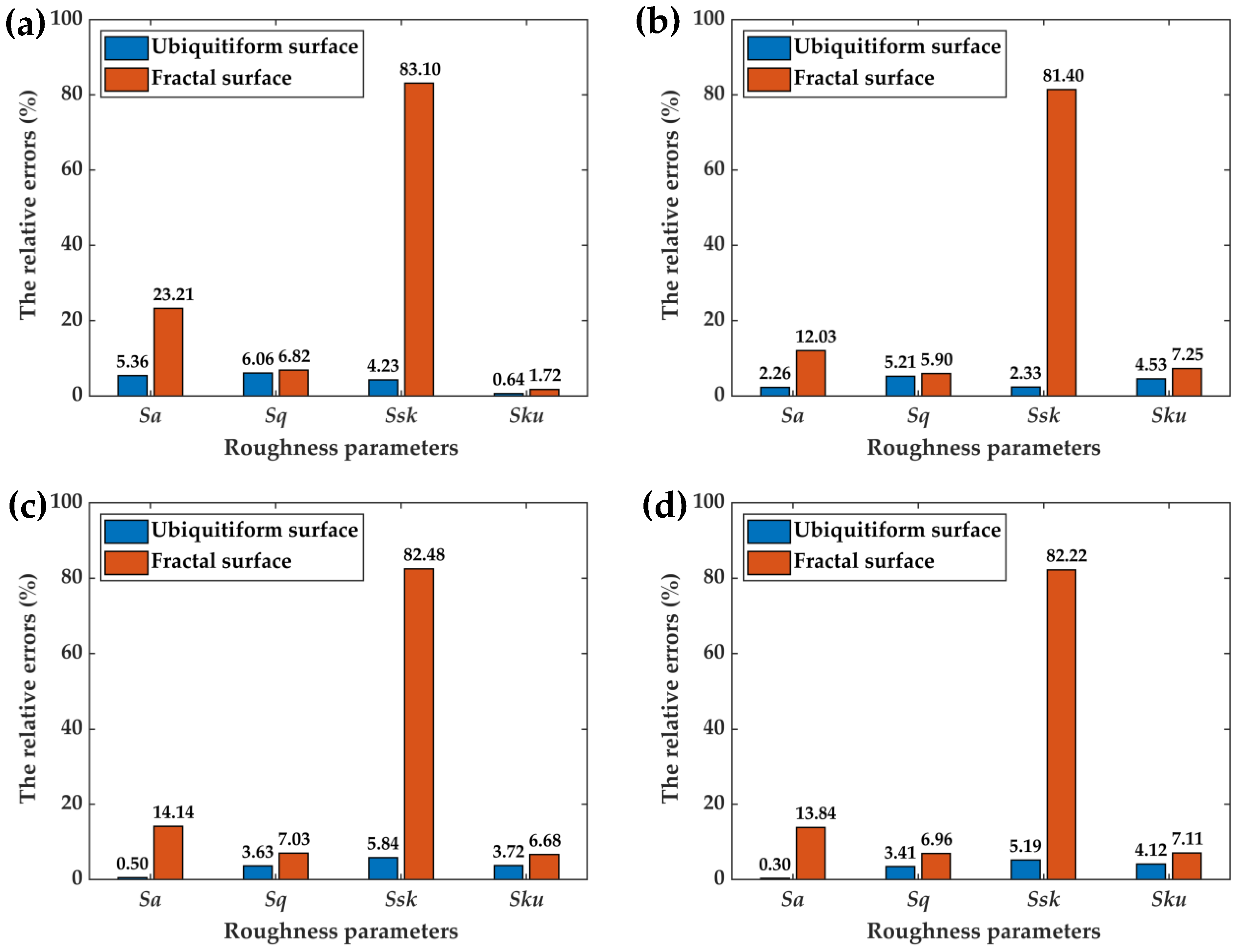
5.2. Different Modeling Methods
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- An, Q.; Suo, S.; Bai, Y. A novel simulation method of micro-topography for grinding surface. Materials 2021, 14, 5128. [Google Scholar] [CrossRef]
- An, Q.; Suo, S.; Lin, F.; Shi, J. A novel micro-contact stiffness model for the grinding surfaces of steel materials based on cosine curve-shaped asperities. Materials 2019, 12, 3561. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; An, Q.; Shang, D.; Bai, L.; Huang, M.; Huang, S. Research on normal contact stiffness of rough joint surfaces machined by turning and grinding. Metals 2022, 12, 669. [Google Scholar] [CrossRef]
- Anand, R.S.; Patra, K. Modeling and simulation of mechanical micro-machining—A review. Mach. Sci. Technol. 2014, 18, 323–347. [Google Scholar] [CrossRef]
- Magsipoc, E.; Zhao, Q.; Grasselli, G. 2D and 3D roughness characterization. Rock Mech. Rock Eng. 2020, 53, 1495–1519. [Google Scholar] [CrossRef]
- Minet, C.; Brunetiere, N.; Tournerie, B.; Fribourg, D. Analysis and modeling of the topography of mechanical seal faces. Tribol. Trans. 2010, 53, 799–815. [Google Scholar] [CrossRef]
- Wu, J.J. Simulation of rough surfaces with FFT. Tribol. Int. 2000, 33, 47–58. [Google Scholar] [CrossRef]
- Wu, J.J. Simulation of non-Gaussian surfaces with FFT. Tribol. Int. 2004, 37, 339–346. [Google Scholar] [CrossRef]
- Johnson, N.L. Systems of frequency curves generated by methods of translation. Biome 1949, 36, 149–176. [Google Scholar] [CrossRef]
- Wang, Y.; Ying, L.; Zhang, G.; Wang, Y. A simulation method for non-Gaussian rough surfaces using FFT and translation process theory. J. Tribol. 2017, 140, 021403. [Google Scholar] [CrossRef]
- Patrikar, R.M. Modeling and simulation of surface roughness. Appl. Surf. Sci. 2004, 228, 213–220. [Google Scholar] [CrossRef]
- Pawlus, P.; Michalczewski, R.; Lenart, A.; Dzierwa, A. The effect of random surface topography height on fretting in dry gross slip conditions. ARCHIVE Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2014, 228, 1374–1391. [Google Scholar] [CrossRef]
- Zhao, G.; Xiong, Z.; Xin, J.; Hou, L.; Gao, W. Prediction of contact stiffness in bolted interface with natural frequency experiment and FE analysis. Tribol. Int. 2018, 127, 157–164. [Google Scholar] [CrossRef]
- Warnecke, G.; Zitt, U. Kinematic simulation for analyzing and predicting high-performance grinding processes. CIRP Annals-Manuf. Technol. 1998, 47, 265–270. [Google Scholar] [CrossRef]
- Saini, D.P. Wheel hardness and local elastic deflections in grinding. Int. J. Mach. Tools Manuf. 1990, 30, 637–649. [Google Scholar] [CrossRef]
- Cooper, W.L.; Lavine, A.S. Grinding process size effect and kinematics numerical analysis. J. Manuf. Sci. Eng. 2000, 122, 59–69. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Butler, D.L. Simulation of precision grinding process, part 1: Generation of the grinding wheel surface. Int. J. Mach. Tools Manuf. 2005, 45, 1321–1328. [Google Scholar] [CrossRef]
- Nguyen, T.A.; Butler, D.L. Simulation of surface grinding process, part 2: Interaction of the abrasive grain with the workpiece. Int. J. Mach. Tools Manuf. 2005, 45, 1329–1336. [Google Scholar] [CrossRef]
- Cao, Y.; Guan, J.; Li, B.; Chen, X.; Yang, J.; Gan, C. Modeling and simulation of grinding surface topography considering wheel vibration. Int. J. Adv. Manuf. Technol. 2013, 66, 937–945. [Google Scholar] [CrossRef]
- Wen, X.N. Modeling and predicting surface roughness for the grinding process. Appl. Mech. Mater. 2014, 599–601, 622–625. [Google Scholar] [CrossRef]
- Chen, S.; Chi, F.C.; Zhang, F.; Zhao, C. Three-dimensional modelling and simulation of vibration marks on surface generation in ultra-precision grinding. Precis. Eng. 2018, 53, 221–235. [Google Scholar] [CrossRef]
- Chen, C.; Tang, J.; Chen, H.; Zhu, C. Research about modeling of grinding workpiece surface topography based on real topography of grinding wheel. Int. J. Adv. Manuf. Technol. 2017, 93, 2411–2421. [Google Scholar] [CrossRef]
- Lipiński, D.; Bałasz, B.; Rypina, Ł. Modelling of surface roughness and grinding forces using artificial neural networks with assessment of the ability to data generalisation. Int. J. Adv. Manuf. Technol. 2018, 94, 1335–1347. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.-L.; Beaucamp, A. Compliant grinding and polishing: A review. Int. J. Mach. Tools Manuf. 2020, 158, 103634. [Google Scholar] [CrossRef]
- Chi, J.; Guo, J.L.; Chen, L.Q. The study on a simulation model of workpiece surface topography in external cylindrical grinding. Int. J. Adv. Manuf. Technol. 2016, 82, 939–950. [Google Scholar] [CrossRef]
- Yp, A.; Ping, Z.A.; Ying, Y.A.; Aa, B.; Yw, A.; Dg, A.; Sgcde, F. New insights into the methods for predicting ground surface roughness in the age of digitalisation. Precis. Eng. 2021, 67, 393–418. [Google Scholar] [CrossRef]
- Sayles, R.S.; Thomas, T.R. Surface topography as a nonstationary random process. Nature 1978, 271, 431–434. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Fractal model of elastic-plastic contact between rough surfaces. J. Tribol.-Trans. ASME 1991, 113, 1–11. [Google Scholar] [CrossRef]
- Ausloos, M.; Berman, D.H. A multivariate Weierstrass–Mandelbrot function. Proc. R. Soc. Lond. A Math. Phys. Sci. 1997, 400, 331–350. [Google Scholar] [CrossRef]
- Yan, W.; Komvopoulos, K. Contact analysis of elastic-plastic fractal surfaces. J. Appl. Phys. 1998, 84, 3617–3624. [Google Scholar] [CrossRef]
- Shi, W.B.; Zhang, Z.S. Contact characteristic parameters modeling for the assembled structure with bolted joints. Tribol. Int. 2022, 165, 107272. [Google Scholar] [CrossRef]
- Zhao, Y.S.; Wu, H.C.; Liu, Z.F.; Cheng, Q.; Yang, C.B. A novel nonlinear contact stiffness model of concrete-steel joint based on the fractal contact theory. Nonlinear Dyn. 2018, 94, 151–164. [Google Scholar] [CrossRef]
- Zheng, J.L.; Liu, X.K.; Jin, Y.; Dong, J.B.; Wang, Q.Q. Effects of surface geometry on advection-diffusion process in rough fractures. Chem. Eng. J. 2021, 414, 128745. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.S.; Chen, X.; Yu, H.C. A spherical conformal contact model considering frictional and microscopic factors based on fractal theory. Chaos Solitons Fractals 2018, 111, 96–107. [Google Scholar] [CrossRef]
- Jiang, K.; Liu, Z.F.; Yang, C.B.; Zhang, C.X.; Tian, Y.; Zhang, T. Effects of the joint surface considering asperity interaction on the bolted joint performance in the bolt tightening process. Tribol. Int. 2022, 167, 107408. [Google Scholar] [CrossRef]
- Li, L.; Yun, Q.Q.; Li, Z.Q.; Liu, Y.; Cao, C.Y. A new contact model of joint surfaces accounting for surface waviness and substrate deformation. Int. J. Appl. Mech. 2019, 11, 1950079. [Google Scholar] [CrossRef]
- Ou, Z.C.; Li, G.Y.; Duan, Z.P.; Huang, F.L. Ubiquitiform in applied mechanics. J. Theor. Appl. Mech. 2014, 52, 37–46. [Google Scholar]
- Yang, M.; Ou, Z.C.; Duan, Z.P.; Huang, F.L. Research on one-dimensional ubiquitiformal constitutive relations for a bimaterial bar. J. Theor. Appl. Mech. 2019, 57, 291–301. [Google Scholar] [CrossRef]
- Li, G.-Y.; Ou, Z.C.; Xie, R.; Duan, Z.-P.; Huang, F.-L. A ubiquitiformal one-dimensional steady-state conduction model for a cellular material rod. Int. J. Thermophys. 2016, 37, 41. [Google Scholar] [CrossRef]
- Ma, Z.; Shi, C.-Z.; Wu, H.-G. Numerical cracking analysis of steel-lined reinforced concrete penstock based on cohesive crack model. Structures 2021, 34, 4694–4703. [Google Scholar] [CrossRef]
- Ou, Z.C.; Li, C.Y.; Duan, Z.P.; Huang, F.L. A stereological ubiquitiformal softening model for concrete. J. Theor. Appl. Mech. 2019, 57, 27–35. [Google Scholar] [CrossRef]
- Ou, Z.C.; Yang, M.; Li, G.Y.; Duan, Z.P.; Huang, F.L. Ubiquitiformal fracture energy. J. Theor. Appl. Mech. 2017, 55, 1101–1108. [Google Scholar] [CrossRef] [Green Version]
- Ou, Z.C.; Ju, Y.B.; Li, J.Y.; Duan, Z.P.; Huang, F.L. Ubiquitiformal crack extension in quasi-brittle materials. AcMSS 2020, 33, 674–691. [Google Scholar] [CrossRef]
- Ju, Y.B.; Ou, Z.C.; Duan, Z.P.; Huang, F.L. The ubiquitiformal characterization of the mesostructures of polymer-bonded explosives. Materials 2019, 12, 3763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shang, S.; Cao, X.; Liu, Z.; Shi, J.P. Analysis of normal elastic contact stiffness of rough surfaces based on ubiquitiform theory. J. Tribol. 2019, 141, 1–25. [Google Scholar] [CrossRef]
- Tian, H.; Li, B.; Liu, H.; Mao, K.; Peng, F.; Huang, X. A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools. Int. J. Mach. Tools Manuf. 2011, 51, 239–249. [Google Scholar] [CrossRef]
- Bigerelle, M.; Guillemot, G.; Khawaja, Z.; Mansori, M.E.; Antoni, J. Relevance of wavelet shape selection in a complex signal. Mech. Syst. Signal Process. 2013, 41, 14–33. [Google Scholar] [CrossRef]
- Chen, B.; Luo, L.; Jiao, H.; Li, S.; Li, S.; Deng, Z.; Yao, H. Affecting factors, optimization, and suppression of grinding marks: A review. Int. J. Adv. Manuf. Technol. 2021, 115, 1–29. [Google Scholar] [CrossRef]
- Freiberg, U.; Kohl, S. Box dimension of fractal attractors and their numerical computation. Commun. Nonlinear Sci. Numer. Simul. 2021, 95, 105615. [Google Scholar] [CrossRef]
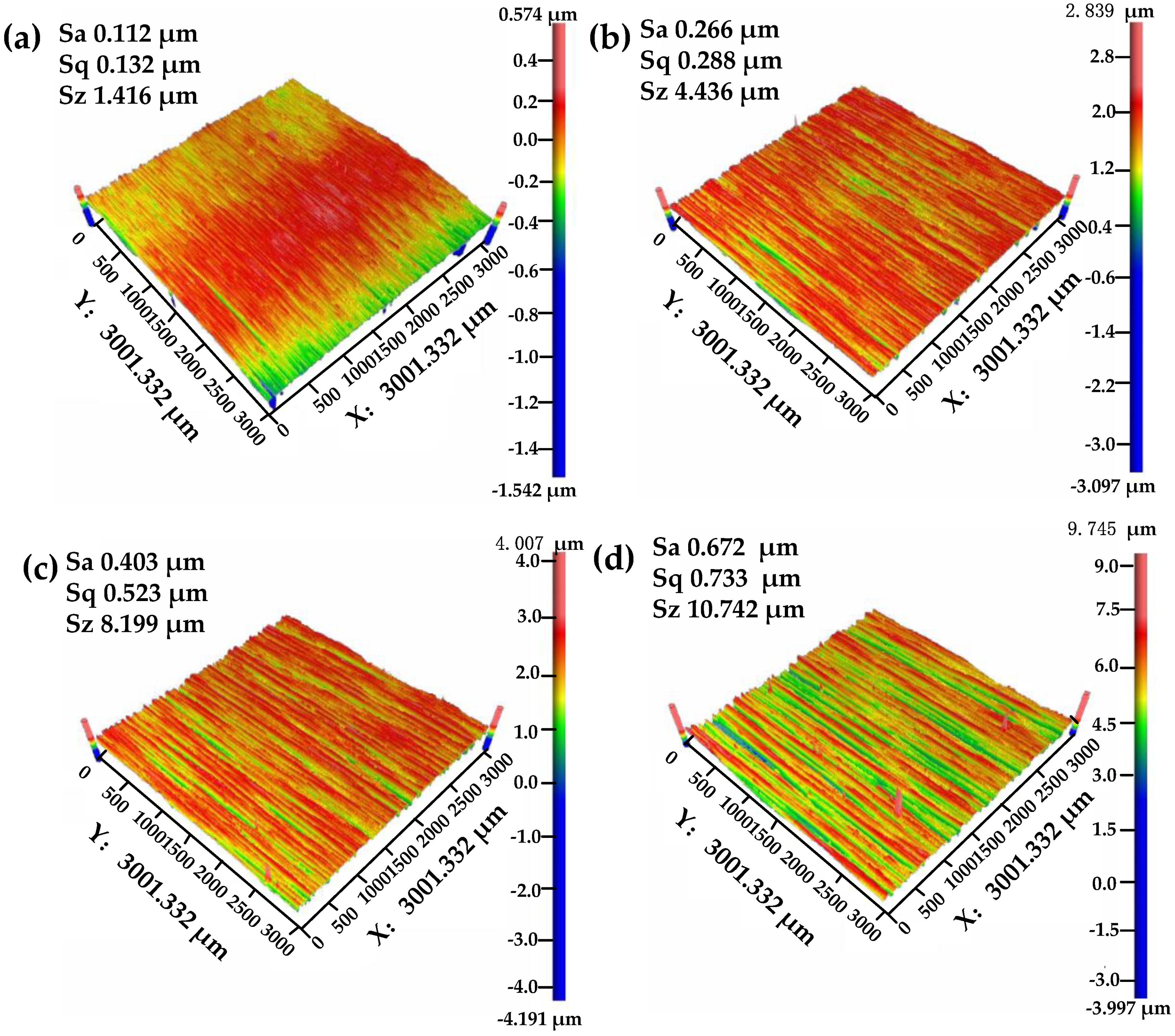
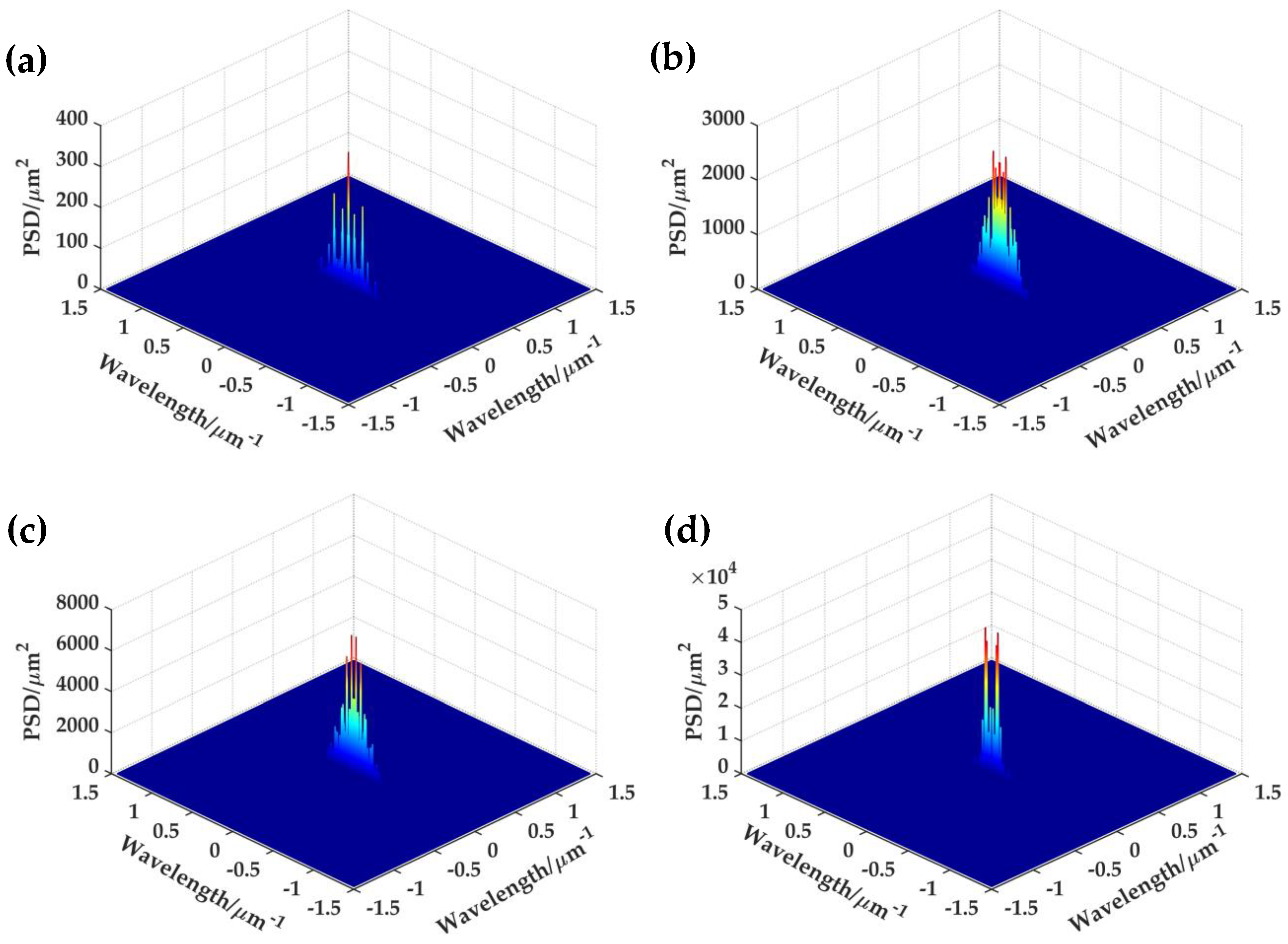

| Fractal Characteristic Parameters | Surface 1 | Surface 2 | Surface 3 | Surface 4 |
|---|---|---|---|---|
| D | 2.553 | 2.517 | 2.497 | 2.491 |
| G | 5.279 × 10−12 | 6.761 × 10−12 | 7.939 × 10−12 | 1.802 × 10−11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; An, Q.; Huang, M.; Shang, D.; Bai, L. A Novel Modeling Method of Micro-Topography for Grinding Surface Based on Ubiquitiform Theory. Fractal Fract. 2022, 6, 341. https://doi.org/10.3390/fractalfract6060341
Liu Y, An Q, Huang M, Shang D, Bai L. A Novel Modeling Method of Micro-Topography for Grinding Surface Based on Ubiquitiform Theory. Fractal and Fractional. 2022; 6(6):341. https://doi.org/10.3390/fractalfract6060341
Chicago/Turabian StyleLiu, Yue, Qi An, Min Huang, Deyong Shang, and Long Bai. 2022. "A Novel Modeling Method of Micro-Topography for Grinding Surface Based on Ubiquitiform Theory" Fractal and Fractional 6, no. 6: 341. https://doi.org/10.3390/fractalfract6060341






