The Passivity of Uncertain Fractional-Order Neural Networks with Time-Varying Delays
Abstract
:1. Introduction
2. Preliminaries
- (1)
- ,
- (2)
- whenever and for some , then the zero solution of system is asymptotically stable.
3. Main Results
3.1. Stability Study of the System
3.2. Passivity Analysis of the System
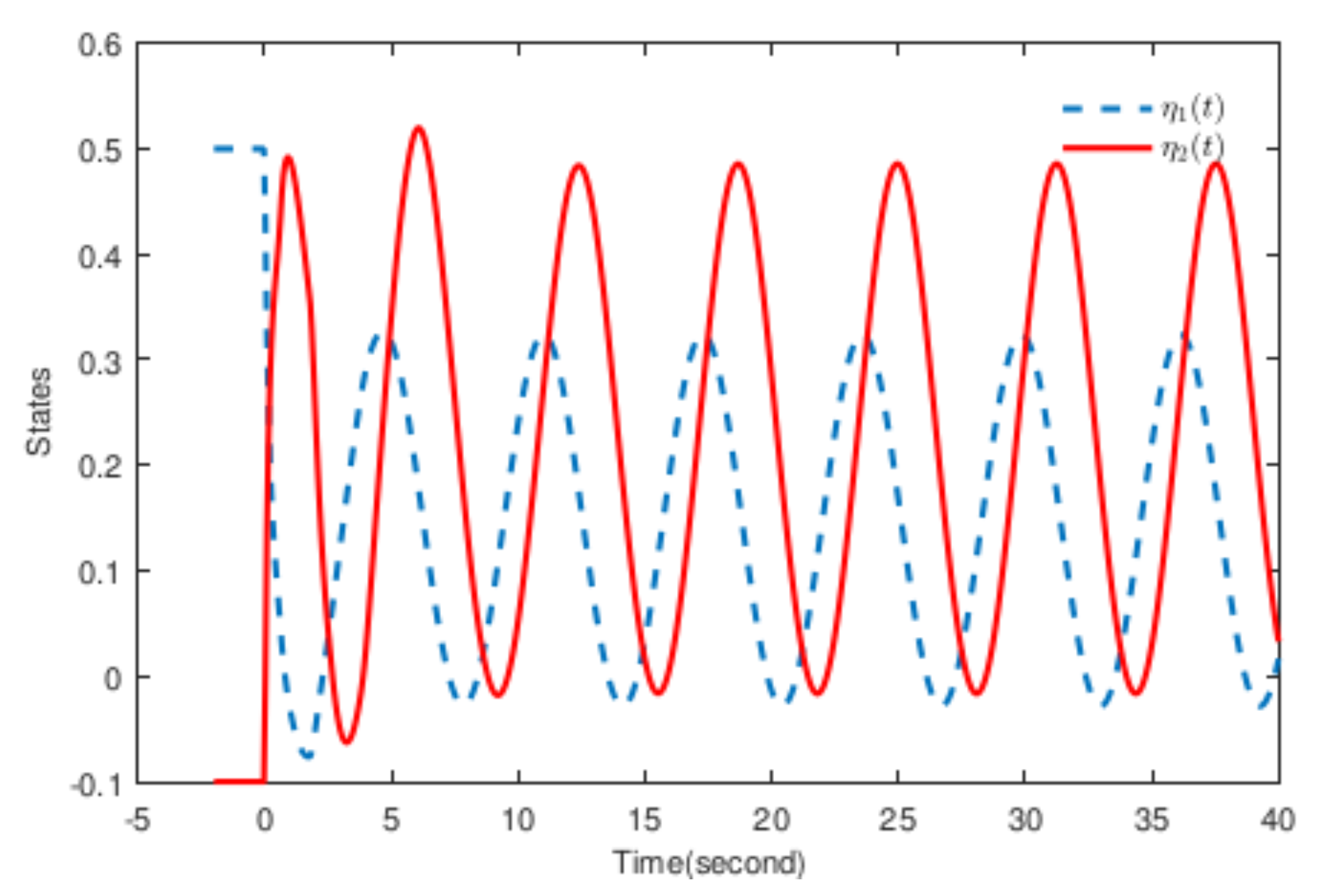
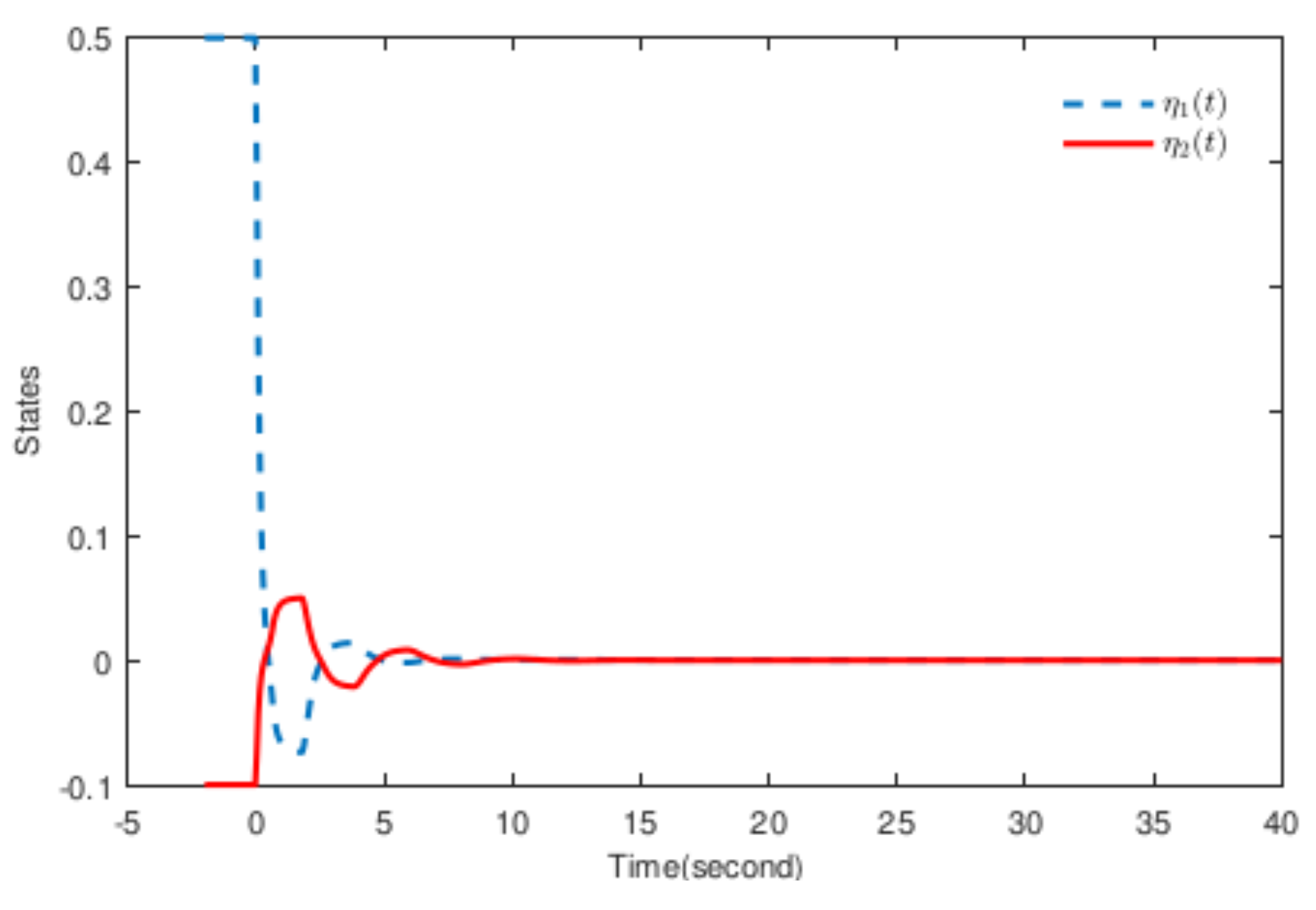
4. Simulation Examples
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kolachalama, V.B.; Singh, P.; Lin, C.Q.; Mun, D.; Belghasem, M.E.; Henderson, J.M.; Francis, J.M.; Salant, D.J.; Chitalia, V.C. Association of pathological fibrosis with renal survival using deep neural networks. Kidney Int. Rep. 2018, 3, 464–475. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, J.; Hui, W.; Li, Q.; Chen, B.; Hao, J.; Jiang, Q.; Shang, X.; Wei, Z. A learning-based framework for miRNA-disease association identification using neural networks. Bioinformatics 2019, 35, 4364–4371. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cherry, K.M.; Qian, L. Scaling up molecular pattern recognition with DNA-based winner-take-all neural networks. Nature 2018, 559, 370–376. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.; Cao, Y.; Iqbal, T.; Wang, Y.; Wang, W.; Plumbley, M.D. Panns: Large-scale pretrained audio neural networks for audio pattern recognition. IEEE/ACM Trans Audio Speech Lang. Process. 2020, 28, 2880–2894. [Google Scholar] [CrossRef]
- Sainath, T.N.; Weiss, R.J.; Wilson, K.W.; Li, B.; Narayanan, A.; Variani, E.; Bacchiani, M.; Shafran, I.; Senior, A.; Chin, K.; et al. Multichannel signal processing with deep neural networks for automatic speech recognition. IEEE/ACM Trans. Audio Speech Lang. Process. 2017, 25, 965–979. [Google Scholar] [CrossRef]
- Pelenis, D.; Barauskas, D.; Vanagas, G.; Dzikaras, M.; Viržonis, D. CMUT-based biosensor with convolutional neural network signal processing. Ultrasonics 2019, 99, 105956. [Google Scholar] [CrossRef]
- Xu, C.J.; Li, P.L. On Finite-Time Stability for Fractional-Order Neural Networks with Proportional Delays. Neural Process. Lett. 2019, 50, 1241–1256. [Google Scholar] [CrossRef]
- Saravanakumar, R.; Stojanovic, S.B.; Radosavljevic, D.D.; Ahn, C.K.; Karimi, H.R. Finite-Time Passivity-Based Stability Criteria for Delayed Discrete-Time Neural Networks via New Weighted Summation Inequalities. IEEE Trans. Neural Networks Learn. Syst. 2018, 30, 58–71. [Google Scholar] [CrossRef]
- Pratap, A.; Raja, R.; Alzabut, J.; Dianavinnarasi, J.; Rajchakit, G. Finite-time Mittag-Leffler stability of fractional-order quaternion-valued memristive neural networks with impulses. Neural Process. Lett. 2020, 51, 1485–1526. [Google Scholar] [CrossRef]
- Wu, Z. Multiple asymptotic stability of fractional-order quaternion-valued neural networks with time-varying delays. Neurocomputing 2021, 448, 301–312. [Google Scholar] [CrossRef]
- Li, J.D.; Wu, Z.B.; Huang, N.J. Asymptotical stability of Riemann-Liouville fractional-order neutral-type delayed projective neural networks. Neural Process. Lett. 2019, 50, 565–579. [Google Scholar] [CrossRef]
- Wang, F.; Yang, Y.; Xu, X.; Li, L. Global asymptotic stability of impulsive fractional-order BAM neural networks with time delay. Neural Comput. Appl. 2017, 28, 345–352. [Google Scholar] [CrossRef]
- Liu, H.; Li, S.; Wang, H.; Sun, Y. Adaptive Fuzzy Control for a Class of Unknown Fractional-Order Neural Networks Subject to Input Nonlinearities and Dead-Zones. Inf. Sci. 2018, 454, 30–45. [Google Scholar] [CrossRef]
- Yang, X.; Li, C.; Huang, T.; Song, Q.; Huang, J. Synchronization of fractional-order memristor-based complex-valued neural networks with uncertain parameters and time delays. Chaos Solitons Fractals 2018, 110, 105–123. [Google Scholar] [CrossRef]
- Huang, X.; Fan, Y.; Jia, J.; Wang, Z.; Li, Y. Quasi-synchronization of fractional-order memristor-based neural networks with parameter mismatches. IET Control. Theory Appl. 2017, 11, 2317–2327. [Google Scholar] [CrossRef]
- Zhang, W.; Cao, J.; Chen, D.; Fuad, A. Synchronization in Fractional-Order Complex-Valued Delayed Neural Networks. Entropy 2018, 20, 54. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Han, Z.; Li, S.; Liu, H. Composite learning sliding mode synchronization of chaotic fractional-order neural networks. J. Adv. Res. 2020, 25, 87–96. [Google Scholar] [CrossRef]
- Thuan, M.V.; Huong, D.C. Robust guaranteed cost control for time-delay fractional-order neural networks systems. Optim. Control. Appl. Methods 2019, 40, 613–625. [Google Scholar] [CrossRef]
- Thuan, M.V.; Binh, T.N.; Huong, D.C. Finite-time guaranteed cost control of Caputo fractional-order neural networks. Asian J. Control. 2020, 22, 696–705. [Google Scholar] [CrossRef]
- Li, F.; Du, C.; Yang, C.; Gui, W. Passivity-based asynchronous sliding mode control for delayed singular Markovian jump systems. IEEE Trans. Autom. Control. 2017, 63, 2715–2721. [Google Scholar] [CrossRef]
- Zhang, M.; Borja, P.; Ortega, R.; Liu, Z.; Su, H. PID passivity-based control of port-Hamiltonian systems. IEEE Trans. Autom. Control. 2017, 63, 1032–1044. [Google Scholar] [CrossRef]
- Yang, B.; Yu, T.; Shu, H.; Zhang, Y.; Chen, J.; Sang, Y.; Jiang, L. Passivity-based sliding-mode control design for optimal power extraction of a PMSG based variable speed wind turbine. Renew. Energy 2018, 119, 577–589. [Google Scholar] [CrossRef]
- Ramos, E.R.; Leyva, R.; Farivar, G.G.; Tafti, H.D.; Townsend, C.D.; Pou, J. Incremental passivity control in multilevel cascaded H-bridge converters. IEEE Trans. Power Electron. 2020, 35, 8766–8778. [Google Scholar] [CrossRef]
- Mehrasa, M.; Babaie, M.; Zafari, A.; Al-Haddad, K. Passivity ANFIS-based control for an intelligent compact multilevel converter. IEEE Trans. Ind. Inform. 2021, 17, 5141–5151. [Google Scholar] [CrossRef]
- Zhang, X.; Fan, X.F.; Xue, Y.; Wang, Y.T.; Cai, W. Robust exponential passive filtering for uncertain neutral-type neural networks with time-varying mixed delays via Wirtinger-based integral inequality. Int. J. Control. Autom. Syst. 2017, 15, 585–594. [Google Scholar] [CrossRef]
- Xiao, Q.; Huang, T.; Zeng, Z. Passivity and passification of fuzzy memristive inertial neural networks on time scales. IEEE Trans. Fuzzy Syst. 2018, 26, 3342–3355. [Google Scholar] [CrossRef]
- Huang, C.; Wang, W.; Cao, J.; Lu, J. Synchronization-based passivity of partially coupled neural networks with event-triggered communication. Neurocomputing 2018, 319, 134–143. [Google Scholar] [CrossRef]
- Zhang, R.; Bilige, S.; Chaolu, T. Fractal solitons, arbitrary function solutions, exact periodic wave and breathers for a nonlinear partial differential equation by using bilinear neural network method. J. Syst. Sci. Complex. 2021, 34, 122–139. [Google Scholar] [CrossRef]
- Thuan, M.V.; Huong, D.C.; Hong, D.T. New results on robust finite-time passivity for fractional-order neural networks with uncertainties. Neural Process. Lett. 2019, 50, 1065–1078. [Google Scholar] [CrossRef]
- Rajchakit, G.; Sriraman, R. Robust passivity and stability analysis of uncertain complex-valued impulsive neural networks with time-varying delays. Neural Process. Lett. 2021, 53, 581–606. [Google Scholar] [CrossRef]
- Park, M.J.; Kwon, O.M.; Ryu, J.H. Passivity and stability analysis of neural networks with time-varying delays via extended free-weighting matrices integral inequality. Neural Netw. 2018, 106, 67–78. [Google Scholar] [CrossRef]
- Ge, C.; Ju, H.P.; Hua, C.; Shi, C. Robust passivity analysis for uncertain neural networks with discrete and distributed time-varying delays. Neurocomputing 2019, 364, 330–337. [Google Scholar] [CrossRef]
- Dai, M.; Xia, J.; Xia, H.; Shen, H. Event-triggered passive synchronization for Markov jump neural networks subject to randomly occurring gain variations. Neurocomputing 2019, 331, 403–411. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, H.; Xue, A.; Lu, R. Passivity analysis of stochastic time-delay neural networks. Nonlinear Dyn. 2010, 61, 71–82. [Google Scholar] [CrossRef]
- Li, N.; Cao, J. Passivity and robust synchronisation of switched interval coupled neural networks with time delay. Int. J. Syst. Sci. 2016, 47, 2827–2836. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Q.; Ge, X.; Zhang, B. Passivity analysis of delayed neural networks based on Lyapunov-Krasovskii functionals with delay-dependent matrices. IEEE Trans. Cybern. 2018, 50, 946–956. [Google Scholar] [CrossRef]
- Ding, Z.; Zeng, Z.; Zhang, H.; Wang, L.; Wang, L. New results on passivity of fractional-order uncertain neural networks. Neurocomputing 2019, 351, 51–59. [Google Scholar] [CrossRef]
- Sau, N.H.; Mai, V.T.; Huyen, N. Passivity analysis of fractional-order neural networks with time-varying delay based on LMI approach. Circuits Syst. Signal Process. 2020, 39, 5906–5925. [Google Scholar] [CrossRef]
- Liu, H.; Pan, Y.; Li, S.; Ye, C. Adaptive Fuzzy Backstepping Control of Fractional-Order Nonlinear Systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2209–2217. [Google Scholar] [CrossRef]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Liu, S.; Yang, R.; Zhou, X.F.; Jiang, W.; Li, X.; Zhao, X.W. Stability analysis of fractional delayed equations and its applications on consensus of multi-agent systems. Commun. Nonlinear Sci. Numer. Simul. 2019, 73, 351–362. [Google Scholar] [CrossRef]
- Zhang, Z.; Mou, S.; Lam, J.; Gao, H. New passivity criteria for neural networks with time-varying delay. Neural Netw. 2009, 22, 864–868. [Google Scholar] [CrossRef]
- Yang, Y.; He, Y.; Wang, Y.; Wu, M. Stability analysis of fractional-order neural networks: An LMI approach. Neurocomputing 2018, 285, 82–93. [Google Scholar] [CrossRef]
- Chen, L.; Chai, Y.; Wu, R.; Zhai, H. Dynamic analysis of a class of fractional-order neural networks with delay. Neurocomputing 2013, 111, 190–194. [Google Scholar] [CrossRef]
- Ding, Z. Passivity analysis of fractional-order neural networks with time-varying parameter uncertainties. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018; pp. 265–268. [Google Scholar]

| The Order | The Passive Parameter |
|---|---|
| 0.1 | |
| 0.2 | 180.3959 |
| 0.3 | 248.7765 |
| 0.4 | 334.8487 |
| 0.5 | 357.8057 |
| 0.6 | 1.6010 |
| 0.7 | 20.5273 |
| 0.8 | 20.3400 |
| 0.9 | 22.4595 |
| 1 | 22.4947 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, S.; Liu, H.; Han, Z. The Passivity of Uncertain Fractional-Order Neural Networks with Time-Varying Delays. Fractal Fract. 2022, 6, 375. https://doi.org/10.3390/fractalfract6070375
Xu S, Liu H, Han Z. The Passivity of Uncertain Fractional-Order Neural Networks with Time-Varying Delays. Fractal and Fractional. 2022; 6(7):375. https://doi.org/10.3390/fractalfract6070375
Chicago/Turabian StyleXu, Song, Heng Liu, and Zhimin Han. 2022. "The Passivity of Uncertain Fractional-Order Neural Networks with Time-Varying Delays" Fractal and Fractional 6, no. 7: 375. https://doi.org/10.3390/fractalfract6070375





