Coupled Fixed Point and Hybrid Generalized Integral Transform Approach to Analyze Fractal Fractional Nonlinear Coupled Burgers Equation
Abstract
:1. Introduction
2. Preliminaries
- , closed, and , where ϖ denotes zero vector in .
- and then .
- If and then .
- , that is , ∀, and if .
- ∀.
- ∀.
3. Existence of Unique Solution
- i.
- is a normal cone and and are completely continuous.
- ii.
- The operators satisfied the Lipschitz condition.
- iii.
- and where and for all .
- iv.
- and .
4. Solution Strategy
5. Convergence Analysis
6. Numerical Examples
- (b)
- When , thenthe exact solutions arewhich is the closed-form solution of integer-order problem.
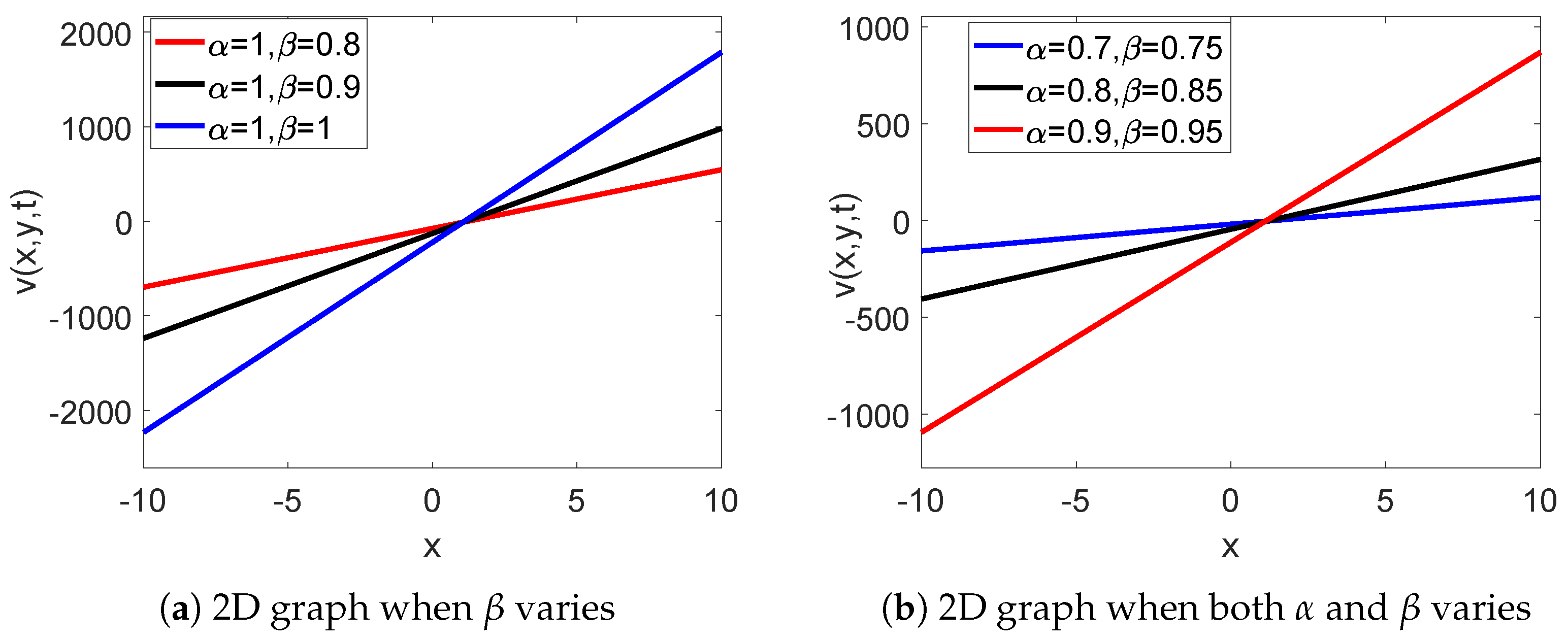
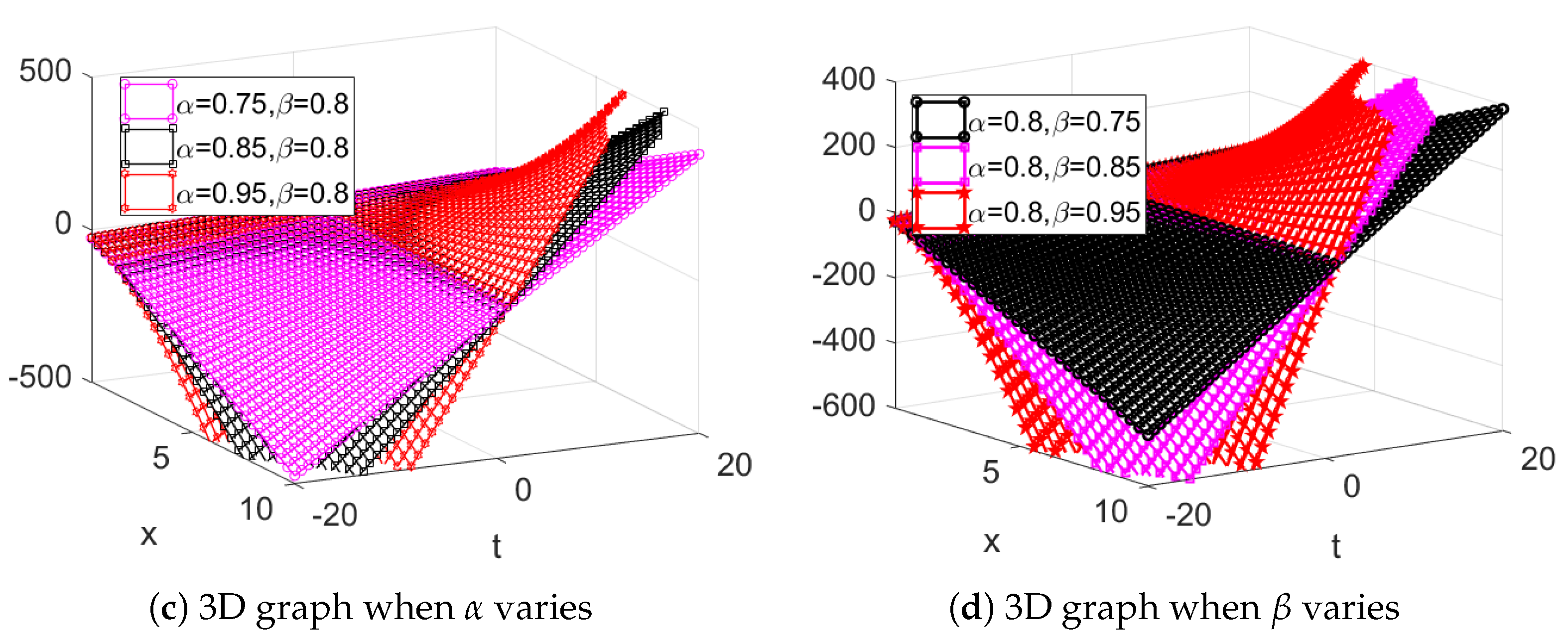
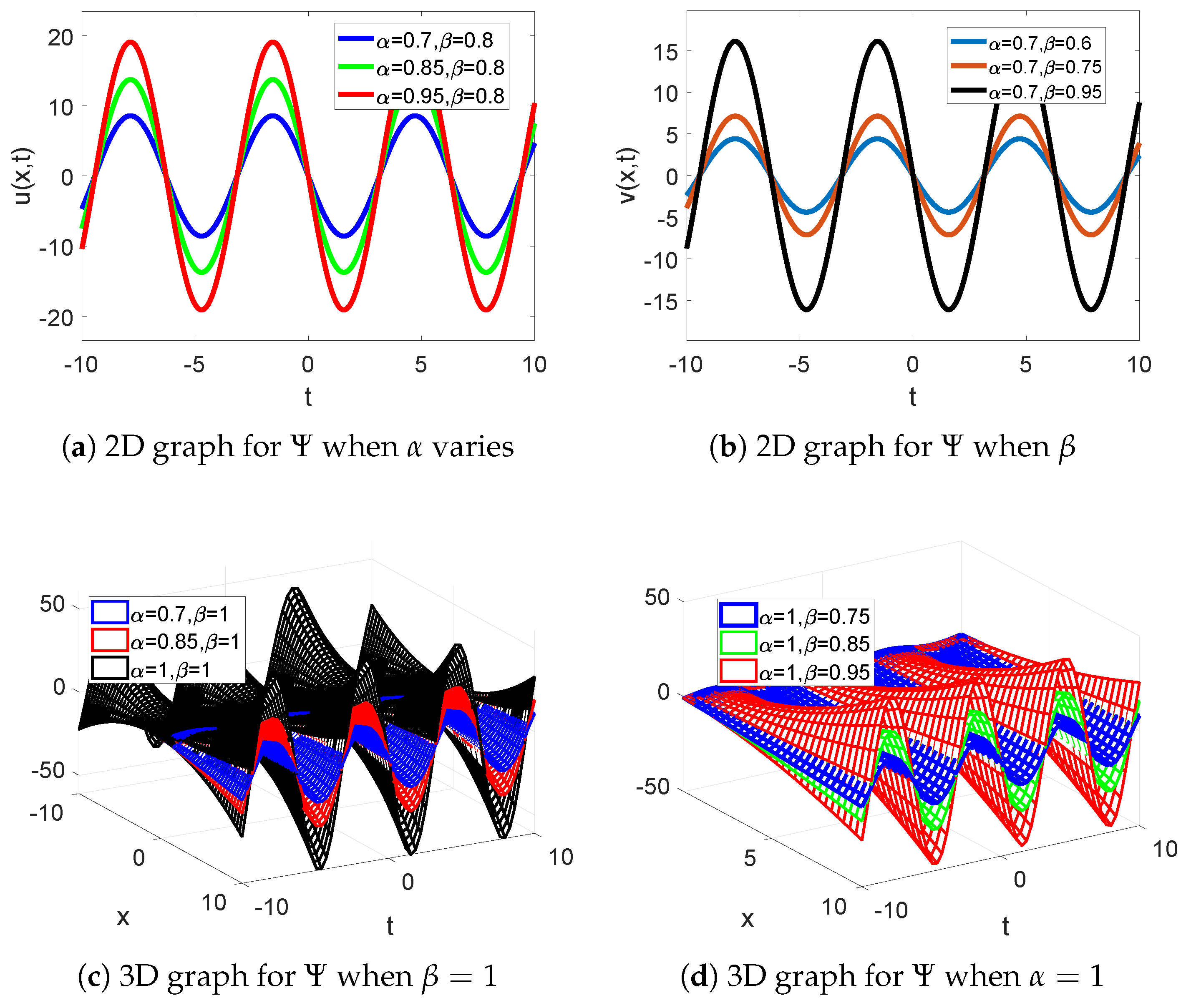
6.1. Simulations and Discussion of Solution of Example 1
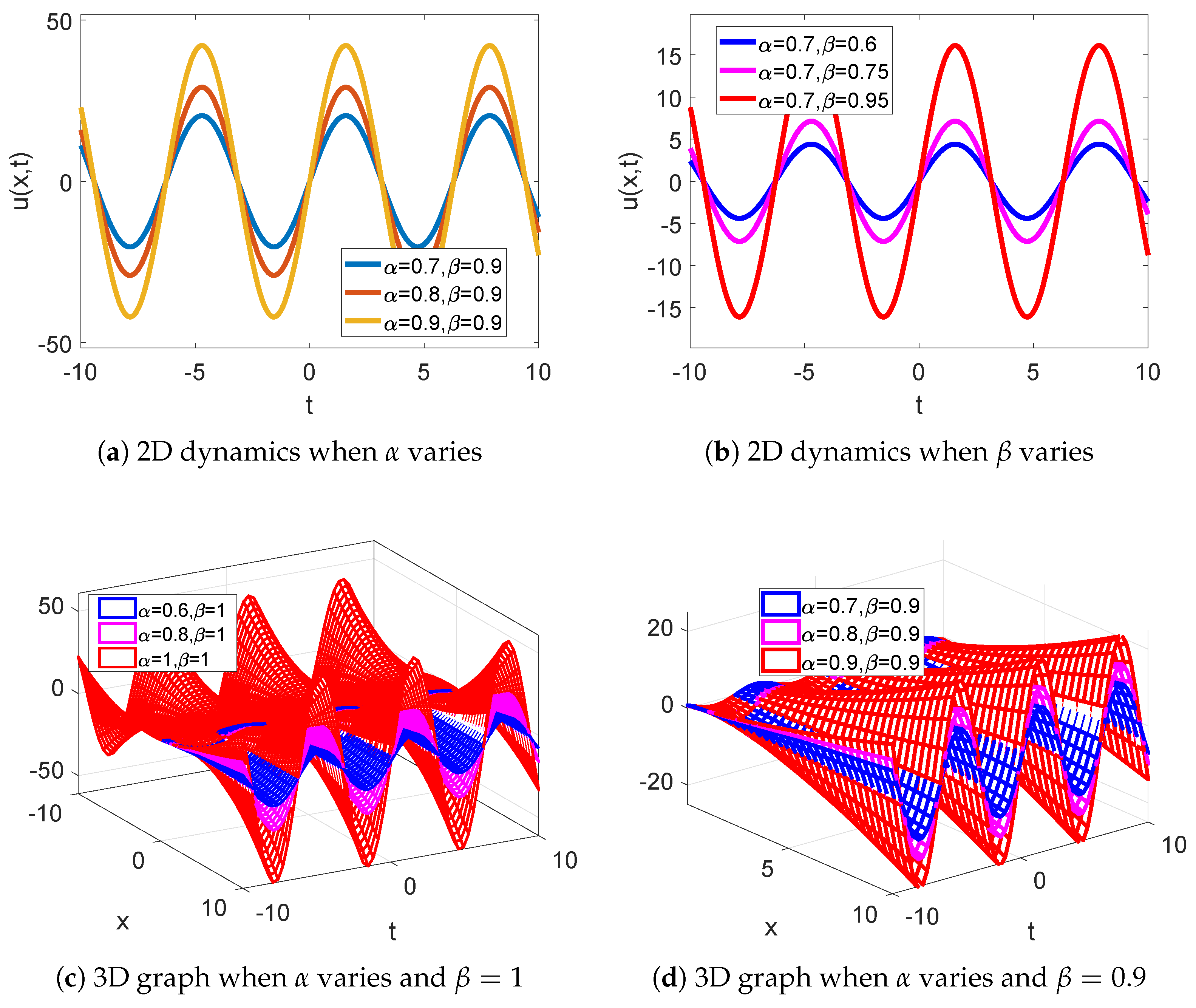
6.2. Simulations and Discussion of Solution of Example 2
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Varsoliwala, A.C.; Singh, T.R. Mathematical modeling of atmospheric internal waves phenomenon and its solution by Elzaki Adomian decomposition method. J. Ocean Eng. Sci. 2022, 7, 203–212. [Google Scholar] [CrossRef]
- Li, Z.; Xia, D.; Cao, J.; Chen, W.; Wang, X. Hydrodynamics study of dolphin’s self-yaw motion realized by spanwise flexibility of caudal fin. J. Ocean Eng. Sci. 2022, 7, 213–224. [Google Scholar] [CrossRef]
- Jaradat, I.; Alquran, M. A variety of physical structures to the generalized equal-width equation derived from Wazwaz-Benjamin-Bona-Mahony model. J. Ocean Eng. Sci. 2022, 7, 244–247. [Google Scholar] [CrossRef]
- Fahim, M.R.A.; Kundu, P.R.; Islam, M.E.; Akbar, M.A.; Osman, M.S. Wave profile analysis of a couple of (3 + 1)-dimensional nonlinear evolution equations by sine-Gordon expansion approach. J. Ocean Eng. Sci. 2022, 7, 272–279. [Google Scholar] [CrossRef]
- Aljahdaly, N.H.; Zobidi, F.O.A. On the Schrödinger equation for deep water waves using the Padé-Adomian decomposition method. J. Ocean Eng. Sci. 2022; in press. [Google Scholar] [CrossRef]
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Abbasbandy, S.; Darvishi, M.T. A numerical solution of Burgers’ equation by modified Adomian method. Appl. Math. Comput. 2005, 163, 1265–1272. [Google Scholar] [CrossRef]
- Bahadir, A.R.; Saglam, M. A mixed finite difference and boundary element approach to one-dimensional Burgers’ equation. Appl. Math. Comput. 2005, 160, 663–673. [Google Scholar] [CrossRef]
- Öziş, T.; Aksan, E.N.; Özdeş, A. A finite element approach for solution of Burgers’ equation. Appl. Math. Comput. 2003, 139, 417–428. [Google Scholar] [CrossRef]
- Kutluay, S.; Bahadir, A.R.; Özdeş, A. Numerical solution of one-dimensional Burgers’ equation: Explicit and exact-explicit finite difference methods. J. Comput. Appl. Math. 1999, 103, 251–261. [Google Scholar] [CrossRef] [Green Version]
- Saifullah, S.; Ali, A.; Irfan, M.; Shah, K. Time-Fractional Klein-Gordon Equation with Solitary/Shock Waves Solutions. Math. Probl. Eng. 2021, 2021, 6858592. [Google Scholar] [CrossRef]
- Ahmad, S.; Ullah, A.; Partohaghighi, M.; Saifullah, S.; Akgül, A.; Jarad, F. Oscillatory and complex behaviour of Caputo-Fabrizio fractional order HIV-1 infection model. AIMS Math. 2022, 7, 4778–4792. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Liu, Z.; Pang, Y.; Liao, M.; Li, P. Bifurcation dynamics and control mechanism of a fractional-order delayed Brusselator chemical reaction model. MATCH Commun. Math. Comput. 2023, 89, 73–106. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Liu, Z.; Pang, Y.; Liao, M.; Aouiti, C. New insight into bifurcation of fractional-order 4D neural networks incorporating two different time delays. Commun. Nonlinear Sci. Numer. Simul. 2023, 118, 107043. [Google Scholar] [CrossRef]
- Ou, W.; Xu, C.; Cui, Q.; Liu, Z.; Pang, Y.; Farman, M.; Ahmad, S.; Zeb, A. Mathematical study on bifurcation dynamics and control mechanism of tri-neuron BAM neural networks including delay. Math. Methods Appl. Sci. 2023. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, W.; Aouiti, C.; Liu, Z.; Yao, L. Bifurcation insight for a fractional-order stage-structured predator-prey system incorporating mixed time delays. Math. Methods Appl. Sci. 2023, 46, 9103–9118. [Google Scholar] [CrossRef]
- Xu, C.; Mu, D.; Pan, Y.; Aouiti, C.; Yao, L. Exploring bifurcation in a fractional-order predator-prey system with mixed delays. J. Appl. Anal. Comput. 2022, 13, 1119–1136. [Google Scholar] [CrossRef]
- Xu, C.; Cui, X.H.; Li, P.L.; Yan, J.L.; Yao, L.Y. Exploration on dynamics in a discrete predator-prey competitive model involving time delays and feedback controls. J. Biol. Dyn. 2023, 17, 2220349. [Google Scholar] [CrossRef] [PubMed]
- Li, P.L.; Lu, Y.J.; Xu, C.J.; Ren, J. Insight into Hopf bifurcation and control methods in fractional order BAM neural networks incorporating symmetric structure and delay. Cogn. Comput. 2023; in press. [Google Scholar] [CrossRef]
- Clavin, P. Instabilities and nonlinear patterns of overdriven detonations in gases. In Nonlinear PDE’s in Condensed Matter and Reactive Flows; Springer: Berlin/Heidelberg, Germany, 2002; pp. 49–97. [Google Scholar]
- Woyczynski, W.A. Lévy processes in the physical sciences. In Lévy Processes; Springer: Berlin/Heidelberg, Germany, 2001; pp. 241–266. [Google Scholar]
- Sugimoto, N. Burgers equation with a fractional derivative; hereditary effects on nonlinear acoustic waves. J. Fluid Mech. 1991, 225, 631–653. [Google Scholar] [CrossRef]
- Funaki, T.; Woyczynski, W. Interacting particle approximation for fractal Burgers equation. In Stochastic Processes and Related Topics; Springer: Berlin/Heidelberg, Germany, 1998; pp. 141–166. [Google Scholar]
- Aljahdaly, N.H.; Agarwal, R.P.; Shah, R.; Botmart, T. Analysis of the Time Fractional-Order Coupled Burgers Equations with Non-Singular Kernel Operators. Mathematics 2021, 9, 2326. [Google Scholar] [CrossRef]
- Shah, N.A.; El-Zahar, E.R.; Chung, J.D. Fractional Analysis of Coupled Burgers Equations within Yang Caputo-Fabrizio Operator. J. Funct. Spaces 2022, 2022, 6231921. [Google Scholar] [CrossRef]
- Mao, Z.; Karniadakis, G.E. Fractional Burgers equation with nonlinear non-locality: Spectral vanishing viscosity and local discontinuous Galerkin methods. J. Comput. Phys. 2017, 336, 143–163. [Google Scholar] [CrossRef]
- Khan, H.; Kumam, P.; Khan, Q.; Khan, S.; Hajira; Arshad, M.; Sitthithakerngkiet, K. The Solution Comparison of Time-Fractional Non-Linear Dynamical Systems by Using Different Techniques. Front. Phys. 2022, 10, 863551. [Google Scholar] [CrossRef]
- Saifullah, S.; Ali, A.; Shah, K.; Promsakon, C. Investigation of Fractal Fractional nonlinear Drinfeld–Sokolov–Wilson system with Non-singular Operators. Results Phys. 2022, 33, 105145. [Google Scholar] [CrossRef]
- Gulalai; Ullah, A.; Ahmad, S.; Inc, M. Fractal fractional analysis of modified KdV equation under three different kernels. J. Ocean Eng. Sci. 2022; in press. [Google Scholar]
- Xuan, L.; Ahmad, S.; Ullah, A.; Saifullah, S.; Akgül, A.; Qu, H. Bifurcations, stability analysis and complex dynamics of Caputo fractal-fractional cancer model. Chaos Solitons Fract. 2022, 159, 112113. [Google Scholar] [CrossRef]
- Saifullah, S.; Ali, A.; Goufo, E.F.D. Investigation of complex behaviour of fractal fractional chaotic attractor with Mittag-Leffler Kernel. Chaos Solitons Fract. 2021, 152, 111332. [Google Scholar] [CrossRef]
- Alqahtani, R.T.; Ahmad, S.; Akgül, A. On Numerical Analysis of Bio-Ethanol Production Model with the Effect of Recycling and Death Rates under Fractal Fractional Operators with Three Different Kernels. Mathematics 2022, 10, 1102. [Google Scholar] [CrossRef]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fract. 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Khan, Z.H.; Khan, W.A. N-transform properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Loonker, D.; Banerji, P.K. Solution of fractional ordinary differential equations by natural transform. Int. J. Math. Eng. Sci. 2013, 12, 1–7. [Google Scholar]
- Khamsi, M. Remarks on Cone Metric Spaces and Fixed Point Theorems of Contractive Mappings. Fixed Point Theory Appl. 2010, 2010, 315398. [Google Scholar] [CrossRef] [Green Version]
- Guo, D.; Lakshmikantham, V. Coupled fixed foints of nonlinear Operators with applications. Nonlinear Anal. Theory Methods Appl. 1987, 11, 623–632. [Google Scholar] [CrossRef]

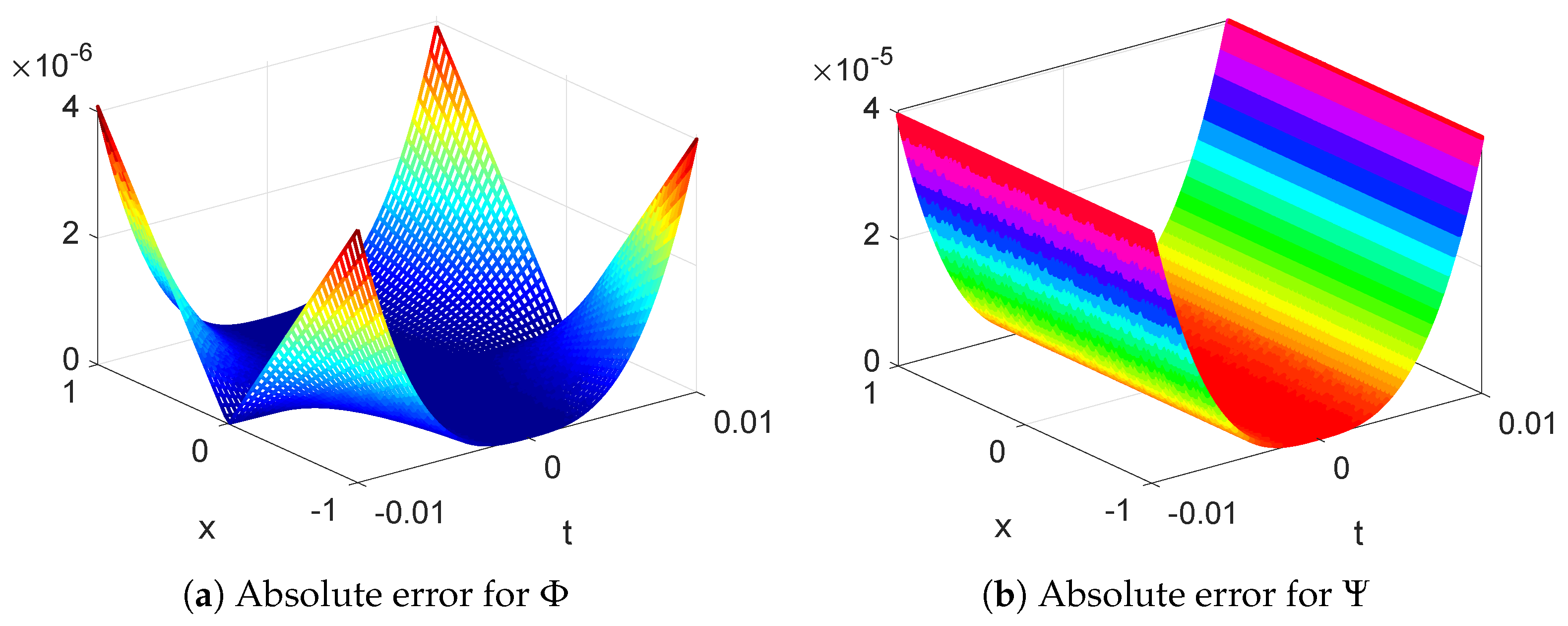
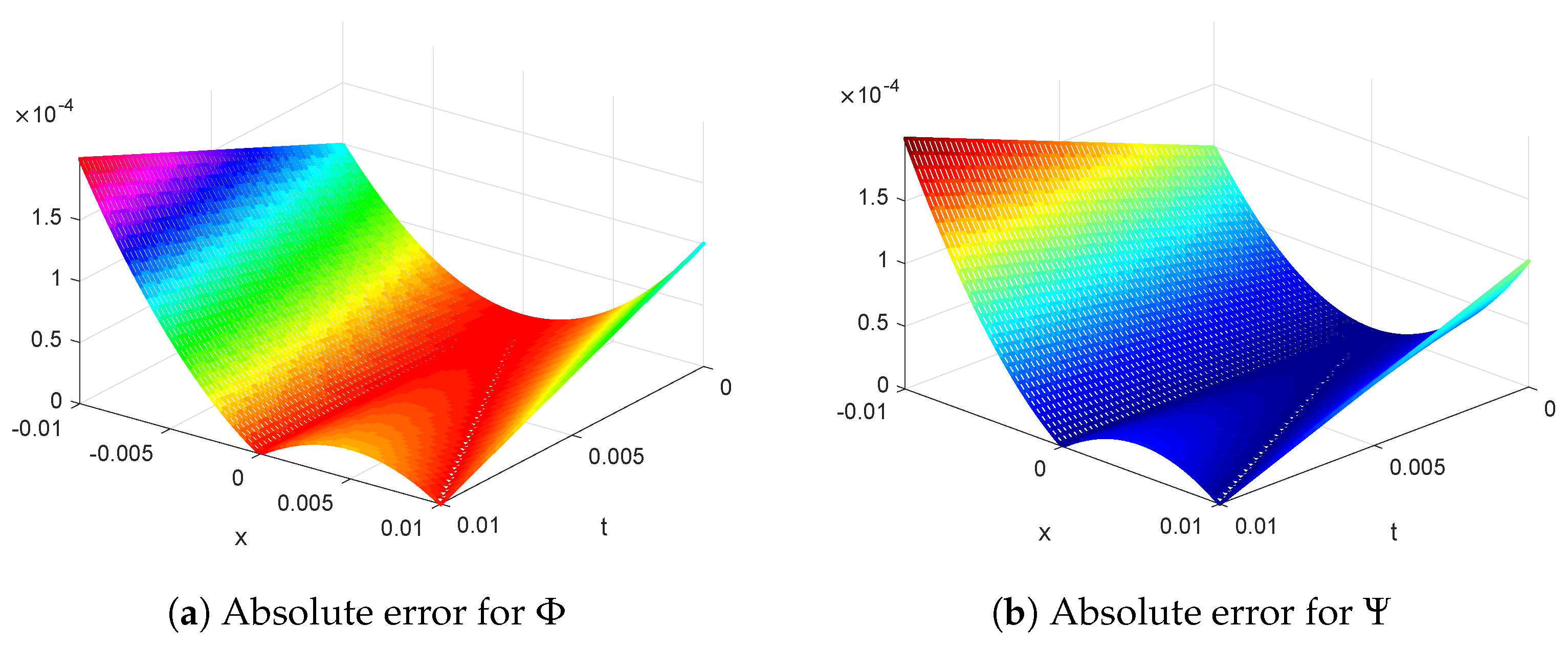

| (, t) | Exact | ∣ Exact− ∣ | (,t) | Exact | ∣ Exact−∣ | ||
|---|---|---|---|---|---|---|---|
| (−1, 0.01) | 9.0218 | 9.0218 | 4.3609e−06 | (−1, 0.01) | −11.2022 | −11.2022 | 4.0448e−05 |
| (−0.8, 0.01) | 9.2178 | 9.2178 | 3.5687e−06 | (−0.8, 0.01) | −11.0022 | −11.0022 | 4.0440e−05 |
| (−0.6, 0.01) | 9.4139 | 9.4139 | 2.7766e−06 | (−0.6, 0.01) | −10.8021 | −10.8021 | 4.0432e−05 |
| (−0.4, 0.01) | 9.6099 | 9.6099 | 1.9844e−06 | (−0.4, 0.01) | −10.6021 | −10.6021 | 4.0424e−05 |
| (−0.2, 0.01) | 9.8060 | 9.8060 | 1.1922e−06 | (−0.2, 0.01) | −10.4020 | −10.4020 | 4.0416e−05 |
| (0, 0.01) | 10.0020 | 10.0020 | 4.0008e−07 | (0, 0.01) | −10.2020 | −10.2020 | 4.0408e−05 |
| (0.2, 0.01) | 10.1980 | 10.1980 | 3.9208e−07 | (0.2, 0.01) | −10.0020 | −10.0020 | 4.0400e−05 |
| (0.4, 0.01) | 10.3941 | 10.3941 | 1.1842e−06 | (0.4, 0.01) | −9.8019 | −9.8020 | 4.0392e−05 |
| (0.6, 0.01) | 10.5901 | 10.5901 | 1.9764e−06 | (0.6, 0.01) | −9.6019 | −9.6019 | 4.0384e−05 |
| (0.8, 0.01) | 10.7862 | 10.7862 | 2.7686e−06 | (0.8, 0.01) | −9.4018 | −9.4019 | 4.0376e−05 |
| (1, 0.01) | 10.9822 | 10.9822 | 3.5607e−06 | (1, 0.01) | −9.2018 | −9.2018 | 4.0368e−05 |
| (, t) | Exact | ∣ Exact− ∣ | (, t) | Exact | ∣ Exact−∣ | ||
|---|---|---|---|---|---|---|---|
| (−0.1, 0.01) | −0.0999 | −0.0903 | 9.6e−03 | (−0.1, 0.01) | 0.0999 | 0.0903 | 9.6e−03 |
| (−0.08, 0.01) | −0.0800 | −0.0738 | 6.2e−03 | (−0.08, 0.01) | 0.0800 | 0.0738 | 6.2e−03 |
| (−0.06, 0.01) | −0.0600 | −0.0565 | 3.6e−03 | (−0.06, 0.01) | 0.0600 | 0.0565 | 3.6e−03 |
| (−0.04, 0.01) | −0.0400 | −0.0384 | 1.6e−03 | (−0.04, 0.01) | 0.0400 | 0.0384 | 1.6e−03 |
| (−0.02, 0.01) | −0.0200 | −0.0196 | 4.1601e−04 | (−0.02, 0.01) | 0.0200 | 0.0196 | 4.1601e−04 |
| (0, 0.01) | 0 | 0 | 0 | (0, 0.01) | 0 | 0 | 0 |
| (0.02, 0.01) | 0.0200 | 0.0204 | 3.8399e−04 | (0.02, 0.01) | −0.0200 | −0.0204 | 3.8399e−04 |
| (0.04, 0.01) | 0.0400 | 0.0416 | 1.6e−03 | (0.04, 0.01) | −0.0400 | −0.0416 | 1.6e−03 |
| (0.06, 0.01) | 0.0600 | 0.0637 | 3.6e−03 | (0.06, 0.01) | −0.0600 | −0.0637 | 3.6e−03 |
| (0.08, 0.01) | 0.0800 | 0.0866 | 6.6e−03 | (0.08, 0.01) | −0.0800 | −0.0866 | 6.6e−03 |
| (0.1, 0.01) | 0.0999 | 0.1103 | 1.4e−03 | (0.1, 0.01) | −0.0999 | −0.1103 | 1.4e−03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouzgarrou, S.M.; Znaidia, S.; Noor, A.; Ahmad, S.; Eldin, S.M. Coupled Fixed Point and Hybrid Generalized Integral Transform Approach to Analyze Fractal Fractional Nonlinear Coupled Burgers Equation. Fractal Fract. 2023, 7, 551. https://doi.org/10.3390/fractalfract7070551
Bouzgarrou SM, Znaidia S, Noor A, Ahmad S, Eldin SM. Coupled Fixed Point and Hybrid Generalized Integral Transform Approach to Analyze Fractal Fractional Nonlinear Coupled Burgers Equation. Fractal and Fractional. 2023; 7(7):551. https://doi.org/10.3390/fractalfract7070551
Chicago/Turabian StyleBouzgarrou, Souhail Mohammed, Sami Znaidia, Adeeb Noor, Shabir Ahmad, and Sayed M. Eldin. 2023. "Coupled Fixed Point and Hybrid Generalized Integral Transform Approach to Analyze Fractal Fractional Nonlinear Coupled Burgers Equation" Fractal and Fractional 7, no. 7: 551. https://doi.org/10.3390/fractalfract7070551







