Robust Fractional-Order PI/PD Controllers for a Cascade Control Structure of Servo Systems
Abstract
:1. Introduction
2. Preliminaries
2.1. Fractional Calculus
2.2. Fractional Linear Model
2.3. The FOPD/FOPI Controller in Frequency Domain
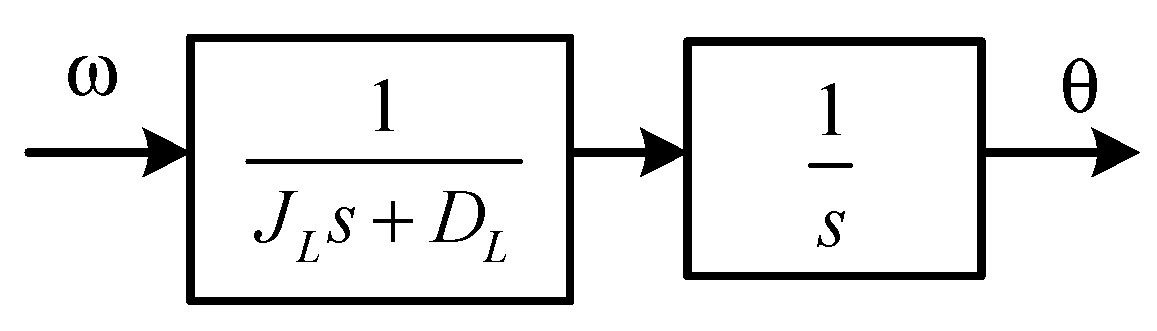
2.4. System Modeling
- Case 1: a ball screw system, also called a feed drive system
- Case 2: a rotational mechanism
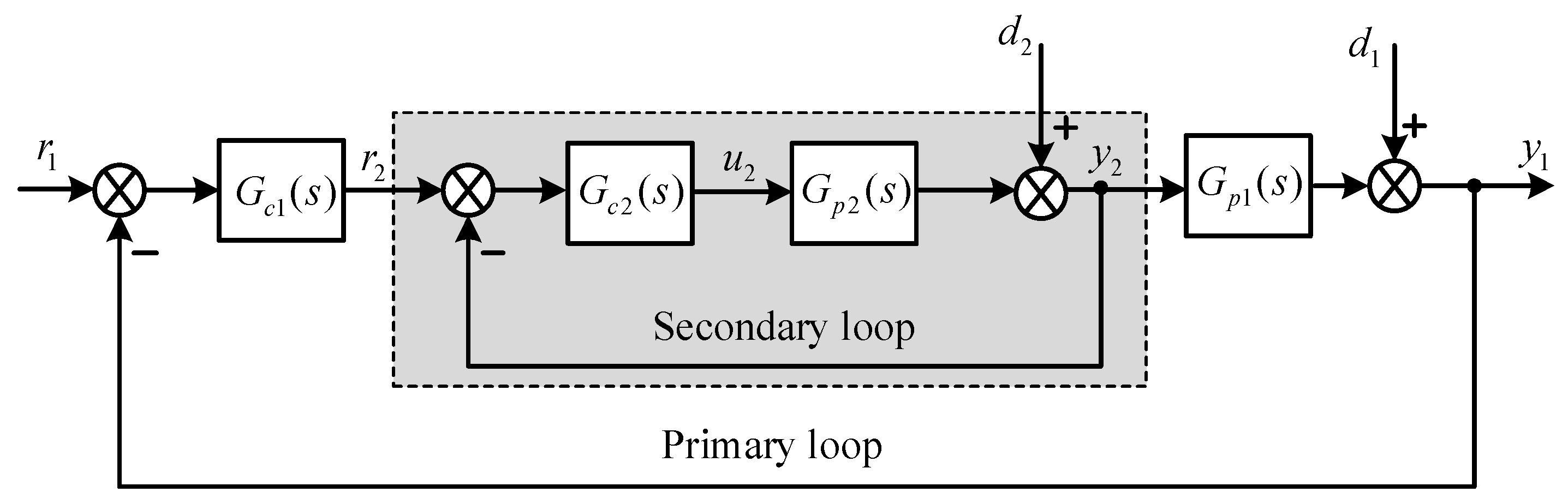
3. Analytical Design of FOPI/FOPD Controllers for the Cascade Scheme
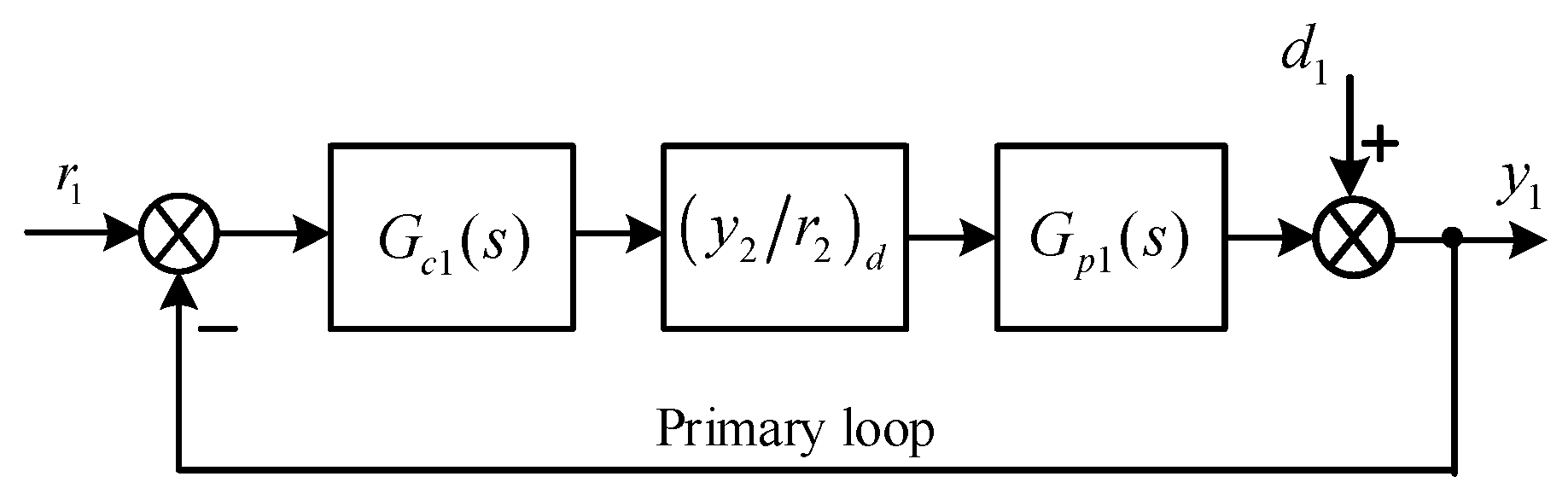
3.1. The Control System Structure
3.2. Design of Secondary Controller-Based Direct Synthesis Method
3.3. FOPD Controller Design for the Primary Control Loop
- Case 1: The primary plant is a feed drive system, so its transfer function is:
- Case 2: The primary plant is a rotational mechanism,
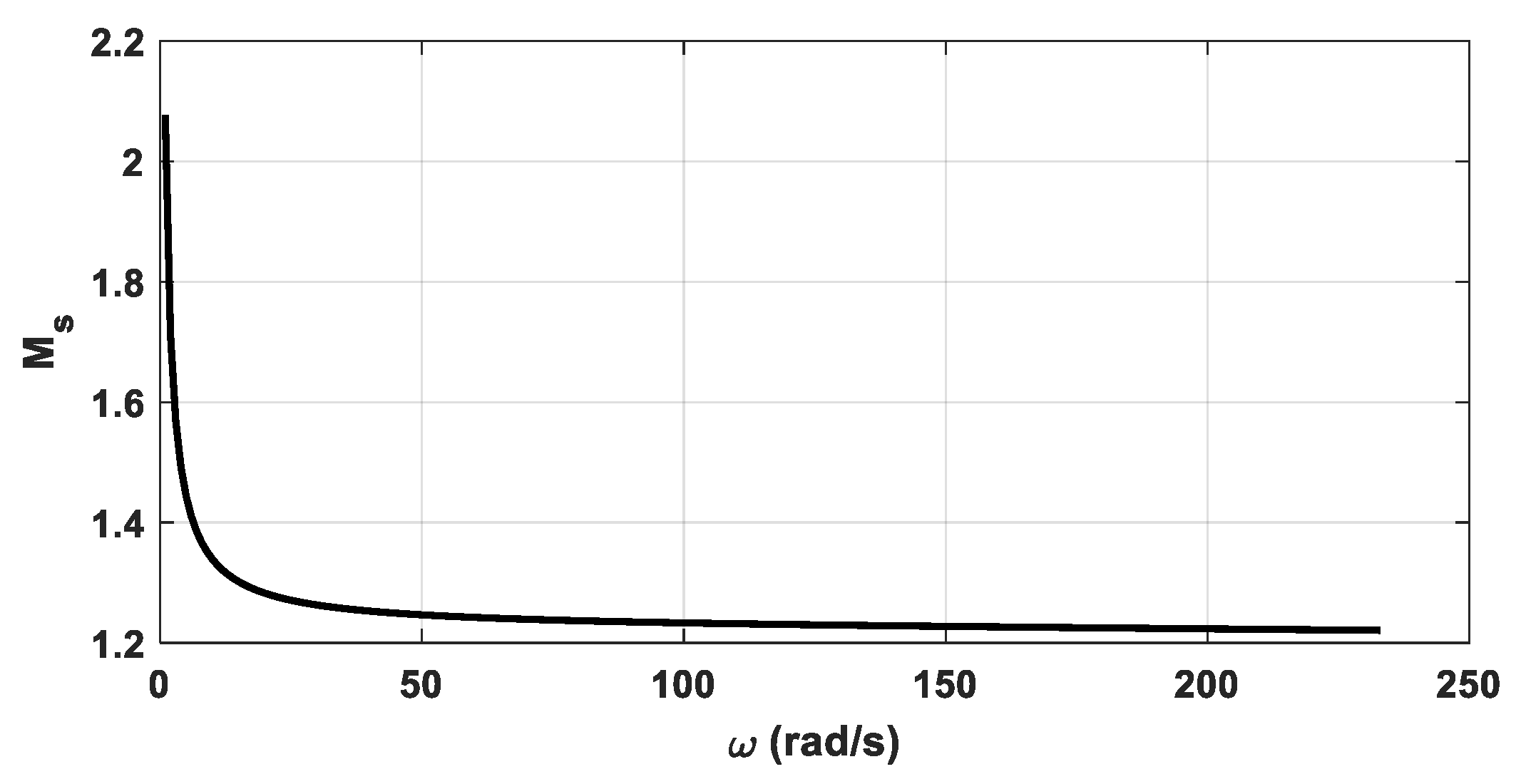
3.4. Tuning Procedure Using Maximum Sensitivity Function
| Algorithm 1: The guideline for tuning parameters based on Ms value |
| 1: Initialization |
| ; choose and |
| 2: while do |
| 3: Compute according to Equations (21) and (22) respectively |
| 4: Calculate Ms for each set of control parameters |
| 5: |
| 6: end while |
| 7: Choose appropriate to get value of Ms being closed to 1.2 |
| 8: end |
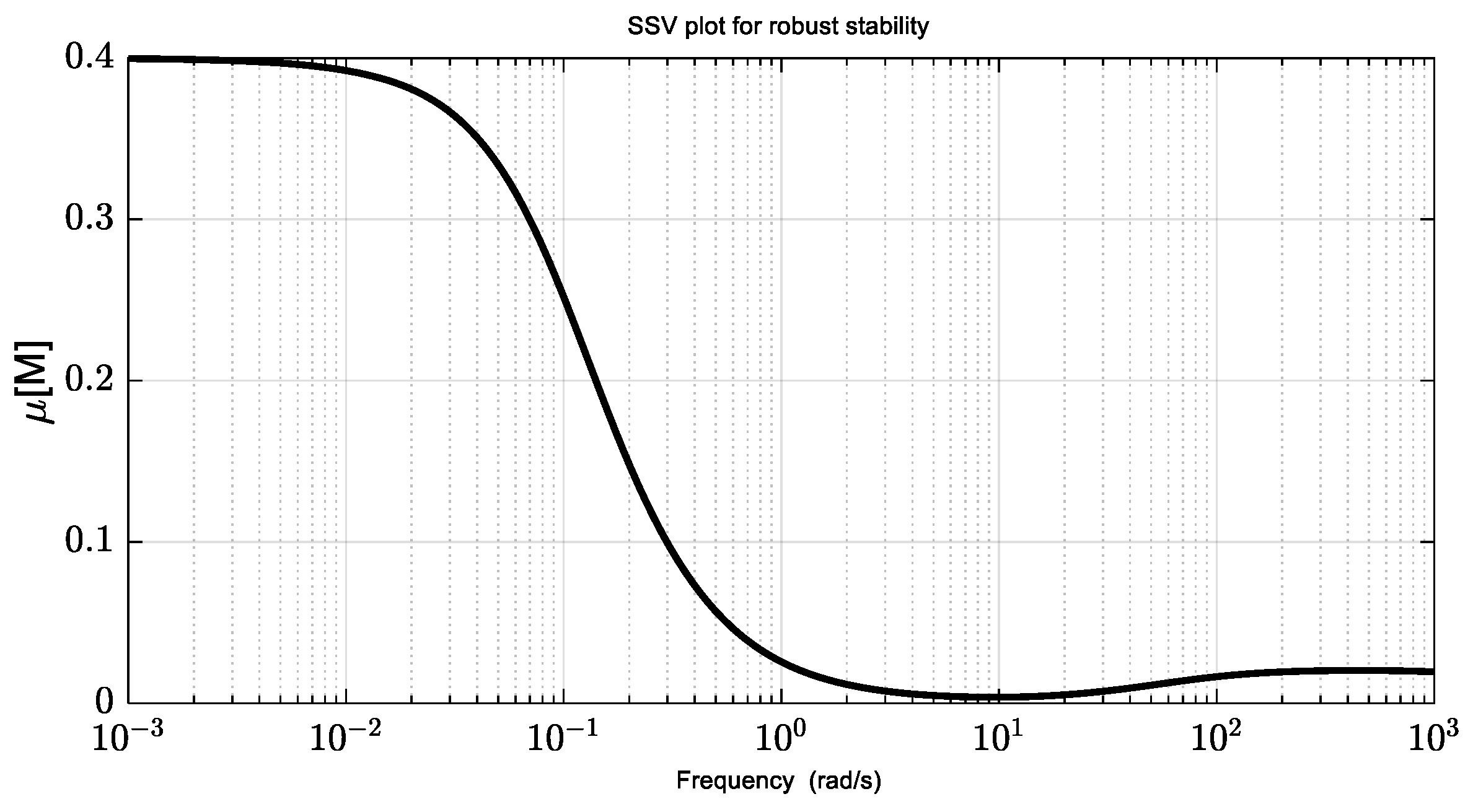
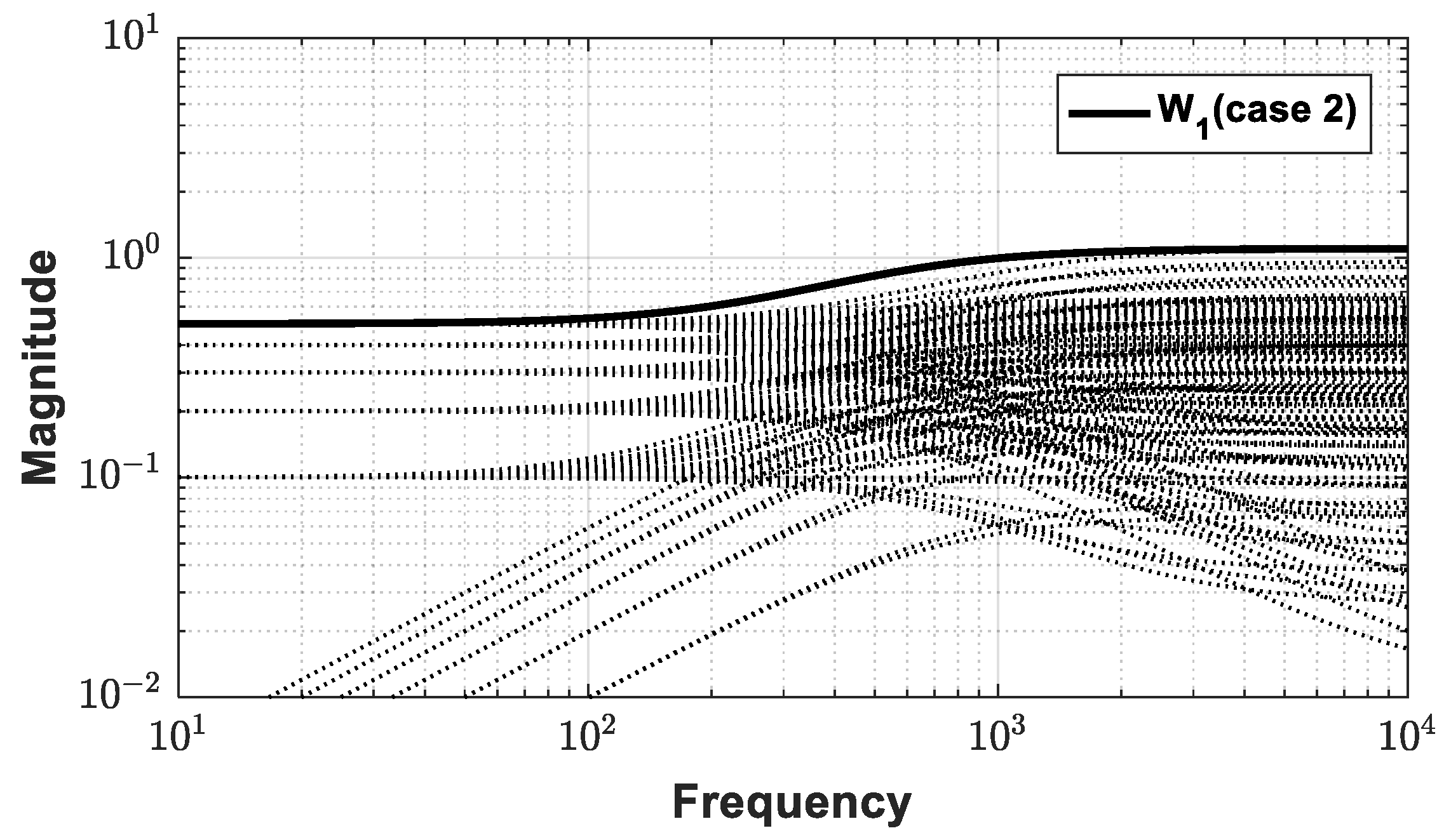
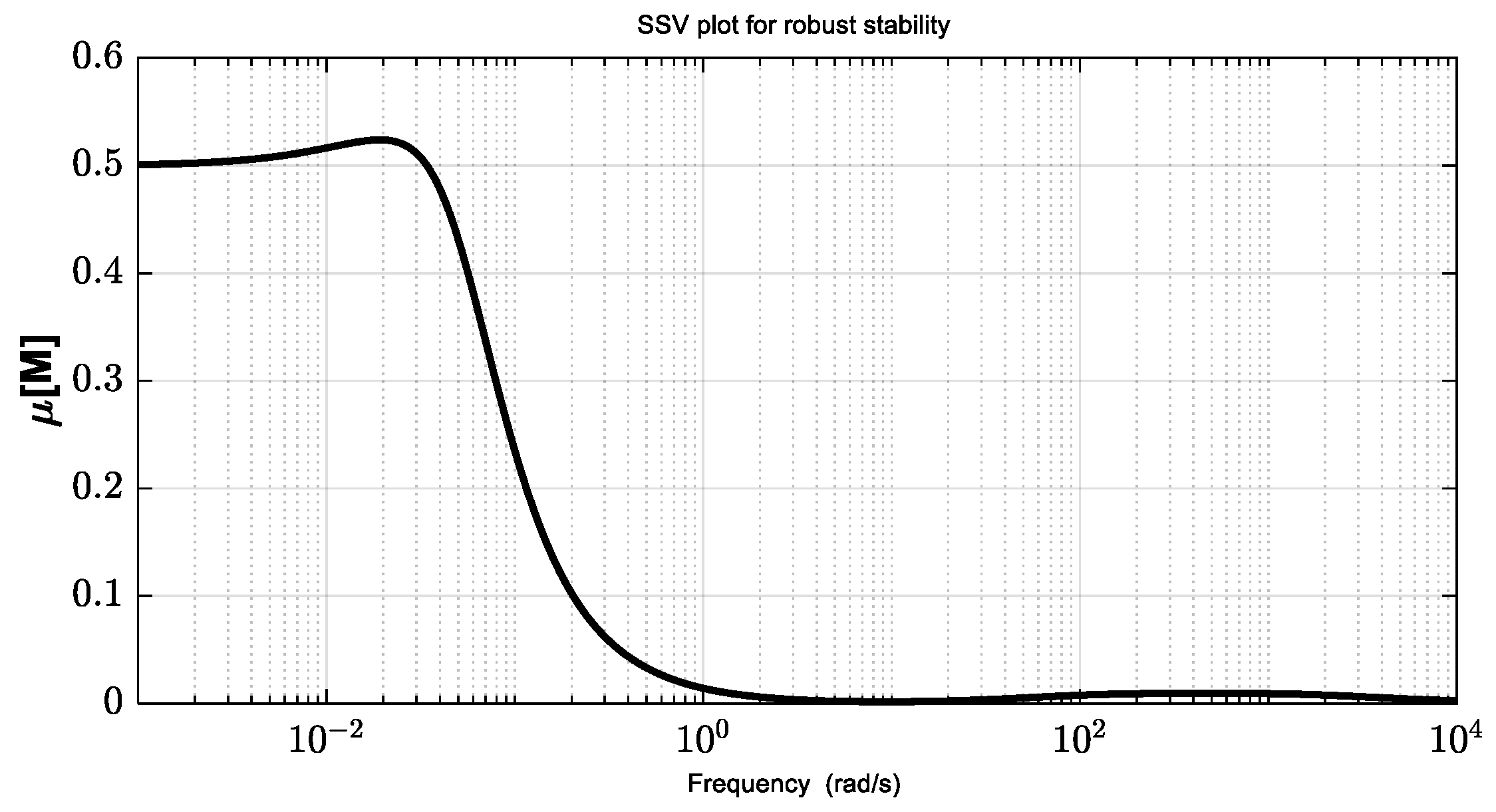
4. Robustness Analysis
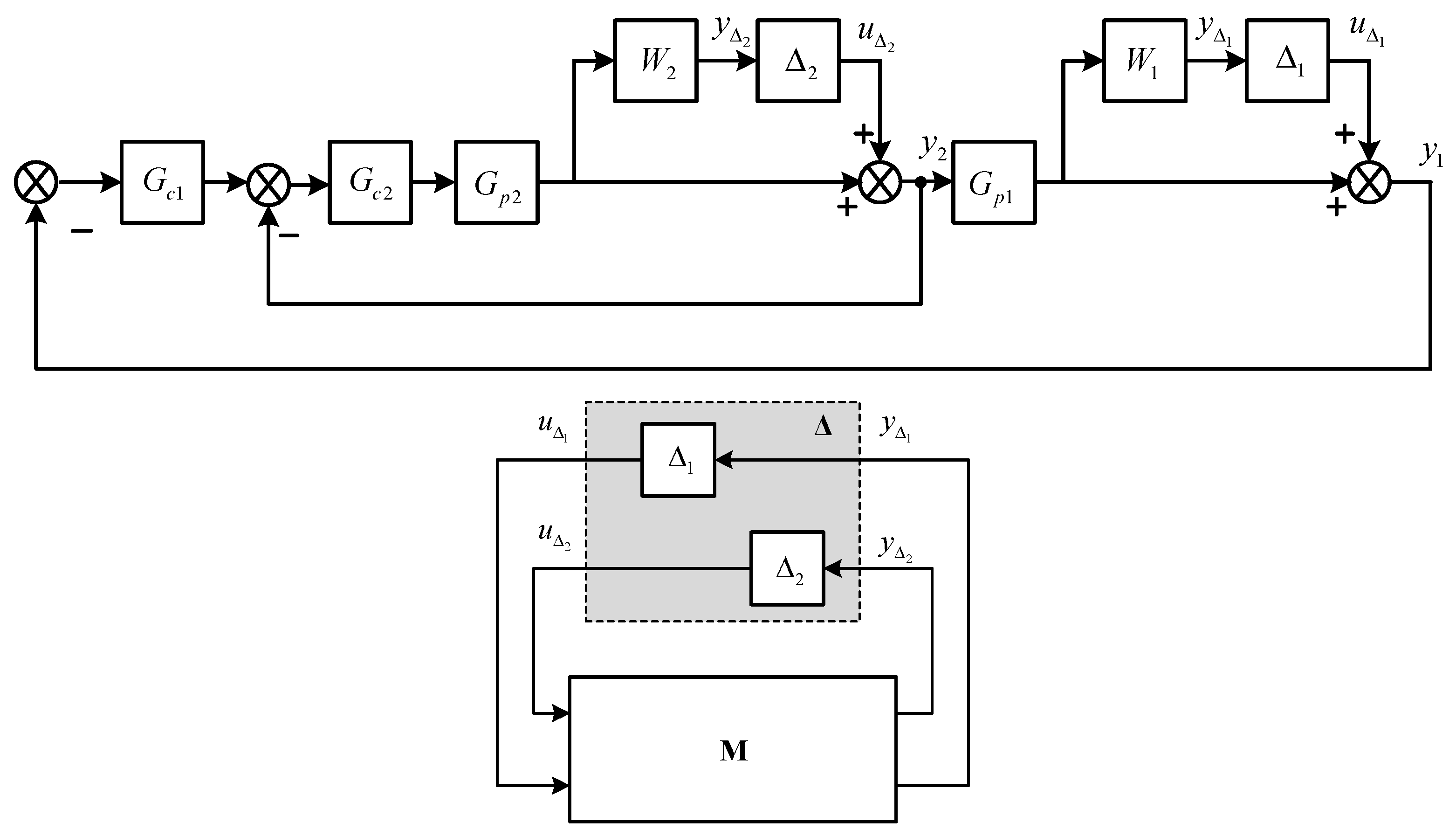
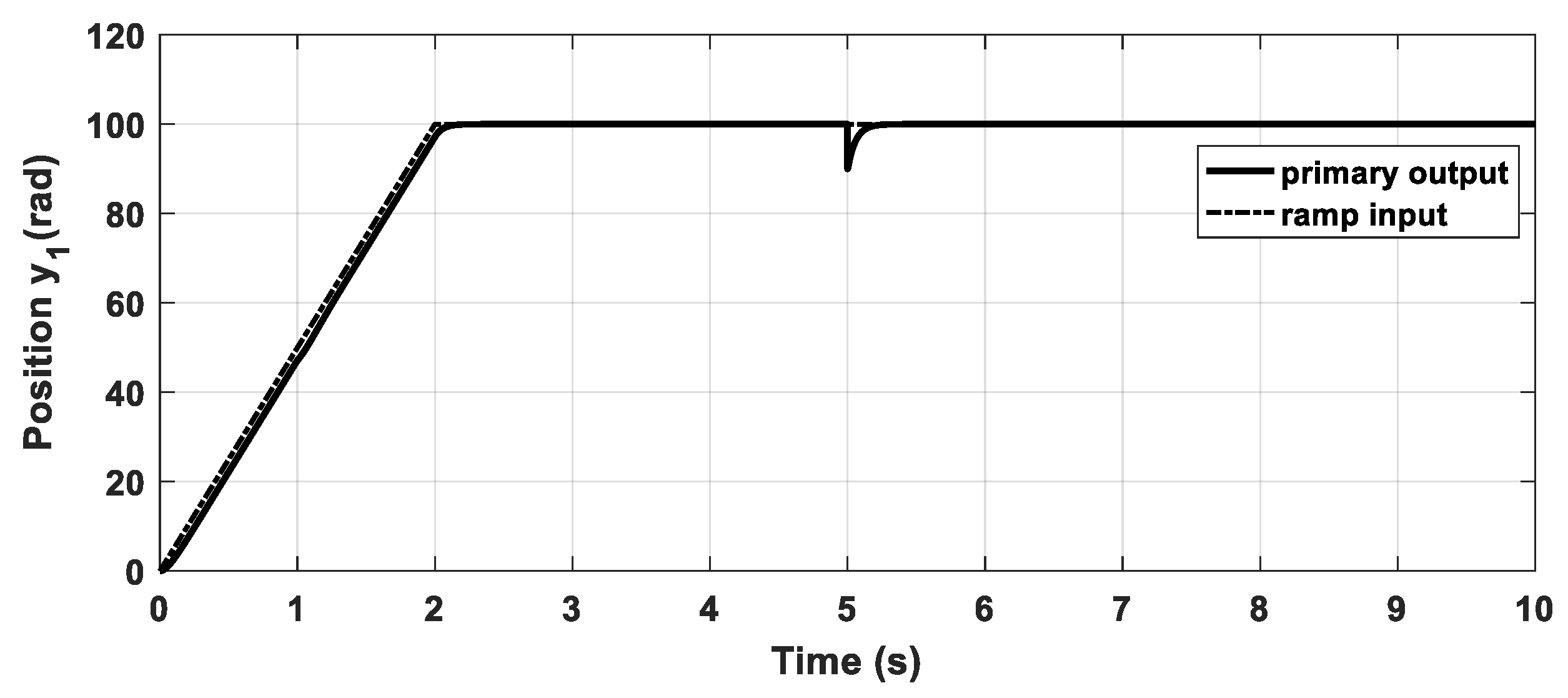
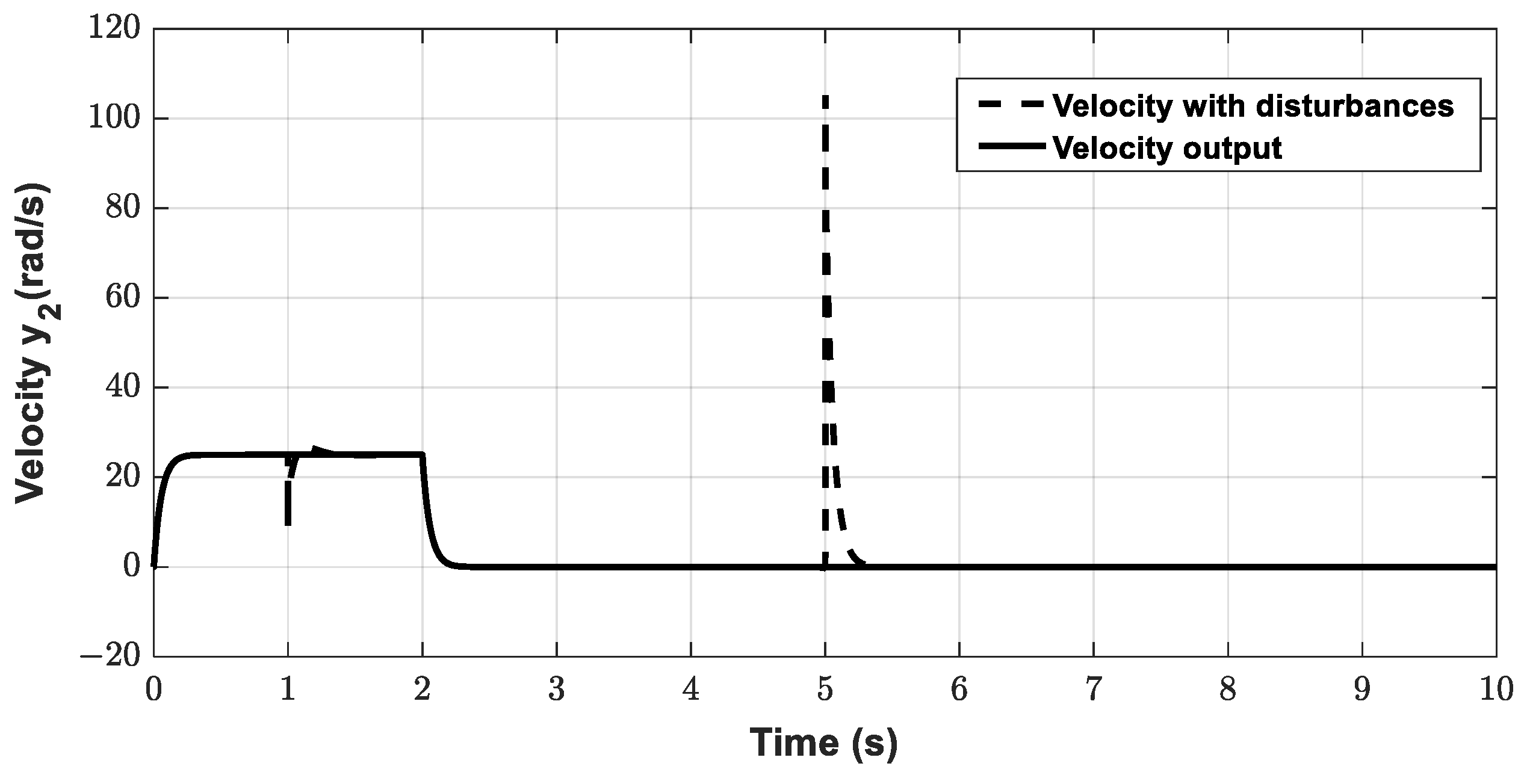
5. Simulation Study
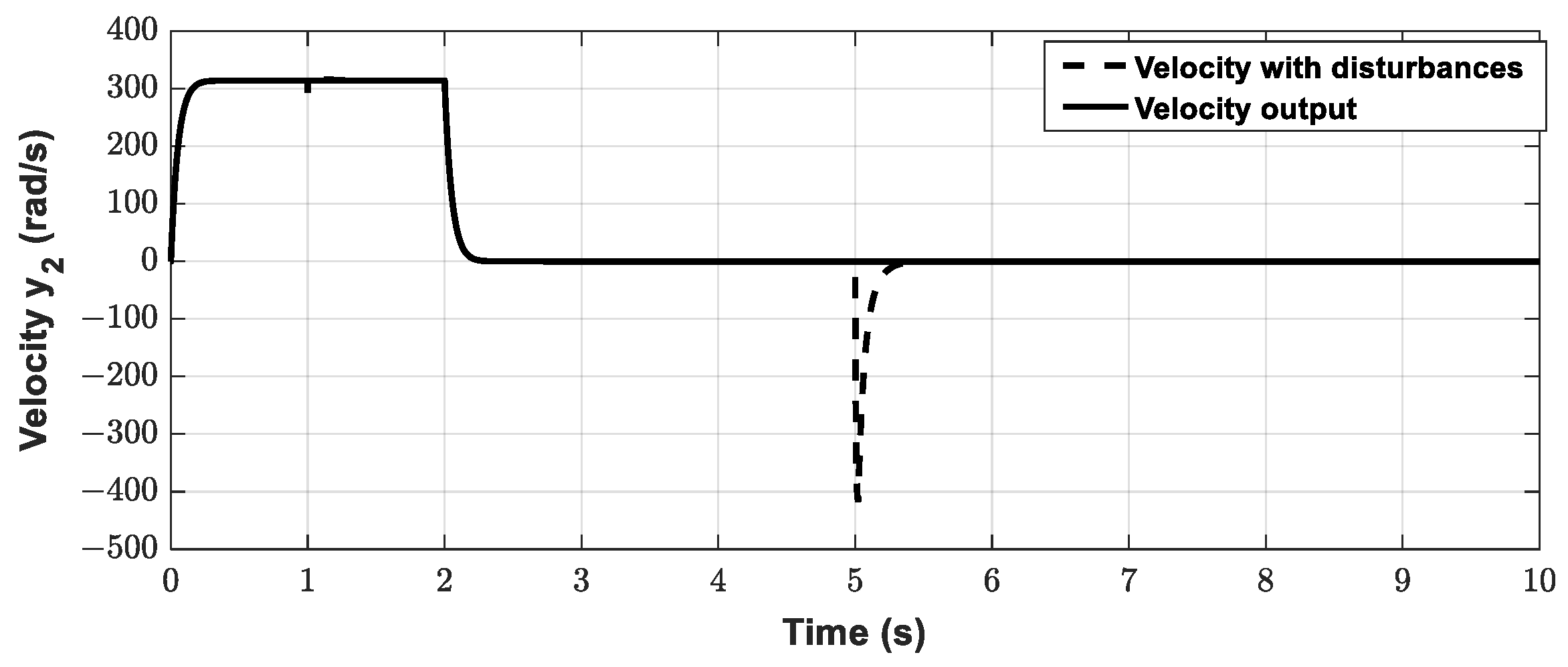
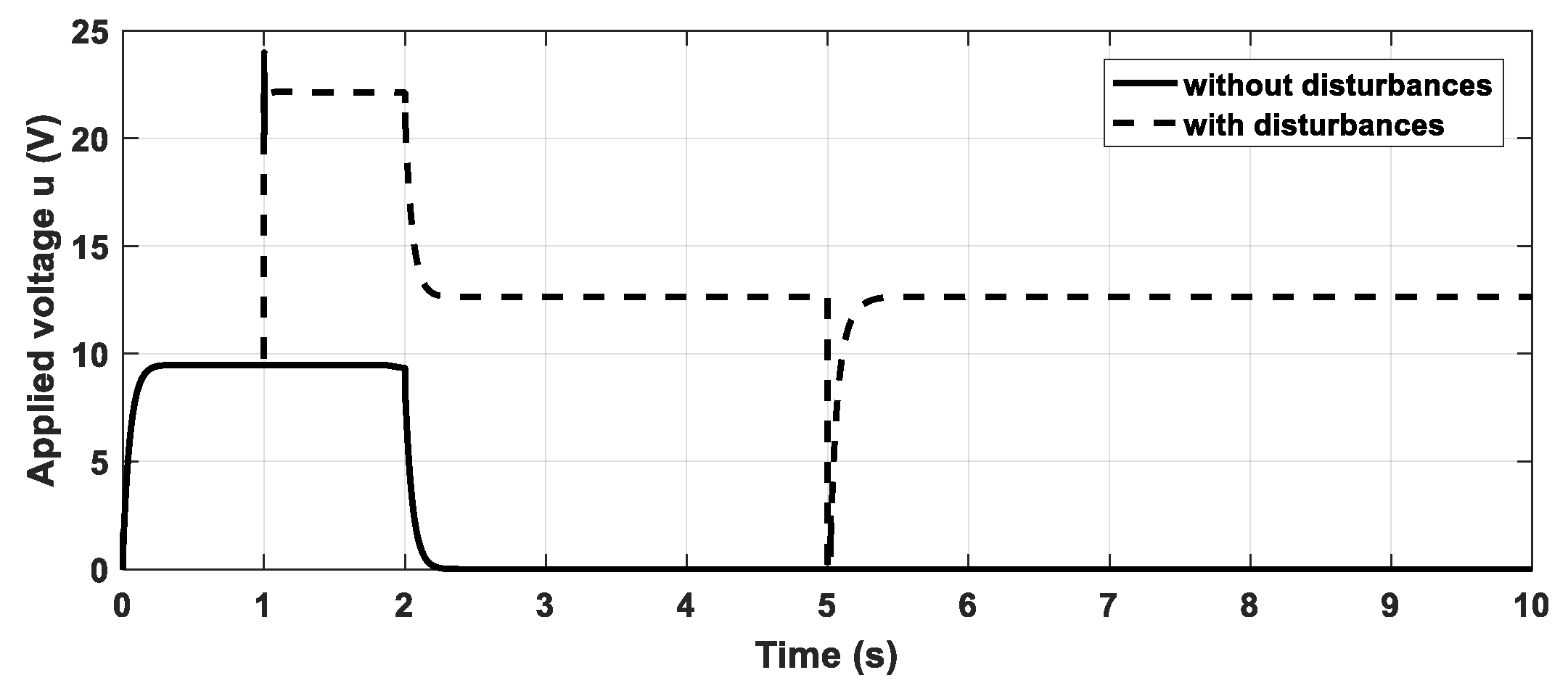
5.1. The Secondary Loop Control Design (Velocity Control)
5.2. The Primary Loop Control Design (Position Control)
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lim, H.; Seo, J.W.; Choi, C.H. Position control of XY table in CNC machining center with non-rigid ball screw. In Proceedings of the 2000 American Control Conference, ACC (IEEE Cat. No. 00CH36334), Chicago, IL, USA, 28–30 June 2000; Volume 3. [Google Scholar]
- Franks, R.G.; Worley, C.W. Quantitative analysis of cascade control. Ind. Eng. Chem. 1956, 48, 1074–1079. [Google Scholar] [CrossRef]
- Chen, J.S.; Huang, Y.; Cheng, K. Mechanical model and contouring analysis of high-speed ball-screw drive systems with compliance effect. Int. J. Adv. Manuf. Technol. 2004, 24, 241–250. [Google Scholar] [CrossRef]
- Altintas, Y.; Verl, A.; Brecher, C.; Uriarte, L.; Pritschow, G. Machine feed drives. CIRP Ann. Manuf. Technol. 2011, 60, 779–796. [Google Scholar] [CrossRef]
- Hwan, S.S.; Kang, S.K.; Chung, D.H.; Stroud, I. Theory and Design of CNC Systems; Springer: Cham, Switzerland, 2008; pp. 157–185. [Google Scholar]
- Nakamura, M.; Goto, S.; Kyura, N. Mechatronic Servo System Control; Springer: Cham, Switzerland, 2004. [Google Scholar]
- Sato, R.; Tsutsumi, M. Mathematical model of feed drive systems consisting of AC servo motor and linear ball guide. J. Jpn. Soc. Precis. Eng. 2005, 71, 633–638. [Google Scholar] [CrossRef]
- Sato, R.; Tsutsumi, M. Modeling and controller tuning techniques for feed drive systems. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005; pp. 669–679. [Google Scholar]
- Liu, Y.; Wang, Z.Z.; Wang, Y.F.; Wang, D.H.; Xu, J.F. Cascade tracking control of servo motor with robust adaptive fuzzy compensation. Inf. Sci. 2021, 569, 450–468. [Google Scholar] [CrossRef]
- Lee, Y.; Park, S.; Lee, M. PID controller tuning to obtain desired closed loop responses for cascade control systems. Ind. Eng. Chem. Res. 1998, 37, 1859–1865. [Google Scholar] [CrossRef]
- Rao, A.S.; Seethaladevi, S.; Uma, S.; Chidambaram, M. Enhancing the performance of parallel cascade control using Smith predictor. ISA Trans. 2009, 48, 220–227. [Google Scholar] [PubMed]
- Uma, S.; Chidambaram, M.; Rao, A.S.; Yoo, C.K. Enhanced control of integrating cascade processes with time delays using modified Smith predictor. Chem. Eng. Sci. 2010, 65, 1065–1075. [Google Scholar] [CrossRef]
- Padhan, D.G.; Majhi, S. An improved parallel cascade control structure for processes with time delay. J. Process Control 2012, 22, 884–898. [Google Scholar] [CrossRef]
- Santosh, S.; Chidambaram, M. A simple method of tuning parallel cascade controllers for unstable FOPTD systems. ISA Trans. 2016, 65, 475–486. [Google Scholar] [CrossRef]
- Raja, G.L.; Ali, A. Modified parallel cascade control strategy for stable, unstable and integrating processes. ISA Trans. 2016, 65, 394–406. [Google Scholar] [CrossRef] [PubMed]
- Raja, G.L.; Ali, A. Smith predictor based parallel cascade control strategy for unstable and integrating processes with large time delay. J. Process Control 2017, 52, 57–65. [Google Scholar] [CrossRef]
- Neubauer, M.; Brenner, F.; Hinze, C.; Verl, A. Cascaded sliding mode position control (SMC-PI) for an improved dynamic behavior of elastic feed drives. Int. J. Mach. Tools Manuf. 2021, 169, 103796. [Google Scholar] [CrossRef]
- Sun, G.; Wu, L.; Kuang, Z.; Ma, Z.; Liu, J. Practical tracking control of linear motor via fractional-order sliding mode. Automatica 2018, 94, 221–235. [Google Scholar] [CrossRef]
- Wang, J.; Shao, C.; Chen, Y.Q. Fractional order sliding mode control via disturbance observer for a class of fractional order systems with mismatched disturbance. Mechatronics 2018, 53, 8–19. [Google Scholar] [CrossRef]
- Wang, S.; Yu, H.; Yu, J. Robust adaptive tracking control for servo mechanisms with continuous friction compensation. Control Eng. Pract. 2019, 87, 76–82. [Google Scholar] [CrossRef]
- Xu, H.; Hinze, C.; Lechler, A.; Verl, A. Robust µ parameterization with low tuning complexity of cascaded control for feed drives. Control Eng. Pract. 2023, 138, 105607. [Google Scholar] [CrossRef]
- Zou, M.; Yu, J.; Ma, Y.; Zhao, L.; Lin, C. Command filtering-based adaptive fuzzy control for permanent magnet synchronous motors with full-state constraints. Inf. Sci. 2020, 546, 1–12. [Google Scholar] [CrossRef]
- Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Metaheuristic-based algorithms for optimizing fractional-order controllers—A recent, systematic, and comprehensive preview. Fractal Fract. 2023, 7, 553. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional-Order Systems and PIλDμ-Controllers. IEEE Trans. Autom. Control 1999, 44, 208–214. [Google Scholar] [CrossRef]
- Padula, F.; Visioli, A. Tuning rules for optimal PID and fractional-order PID controllers. J. Process Control 2011, 21, 69–81. [Google Scholar] [CrossRef]
- Vu, T.N.L.; Lee, M. Analytical design of fractional-order proportional-integral controllers for time-delay processes. ISA Trans. 2013, 52, 583–591. [Google Scholar] [CrossRef] [PubMed]
- Beschi, M.; Padula, F.; Visioli, A. Fractional robust PID control of a solar furnace. Control Eng. Pract. 2016, 56, 190–199. [Google Scholar] [CrossRef]
- Li, D.; Liu, L.; Jin, Q.; Hirasawa, K. Maximum sensitivity based fractional IMC-PID controller design for non-integer order system with time delay. J. Process Control 2015, 31, 17–29. [Google Scholar] [CrossRef]
- Vilanova, R.; Arrieta, O.; Ponsa, P. Robust PI/PID controllers for load disturbance based on direct synthesis. ISA Trans. 2018, 81, 177–196. [Google Scholar] [CrossRef] [PubMed]
- Yumuk, E.; Guzelkaya, M.; Eksin, I. Analytical fractional PID controller design based on Bode’s ideal transfer function plus time delay. ISA Trans. 2019, 91, 196–206. [Google Scholar] [CrossRef]
- Moradi, M. A genetic-multivariable fractional order PID control to multi-input multi-output processes. J. Process Control 2014, 24, 336–343. [Google Scholar] [CrossRef]
- Sánchez, H.S.; Padula, F.; Visioli, A.; Vilanova, R. Tuning rules for robust FOPID controllers based on multi-objective optimization with FOPDT models. ISA Trans. 2017, 66, 334–361. [Google Scholar] [CrossRef] [PubMed]
- Tumari, M.Z.M.; Ahmad, M.A.; Suid, M.H.; Hao, M.R. An improved marine predators algorithm-tuned fractional-order PID controller for automatic voltage regulator systems. Fractal Fract. 2023, 7, 571. [Google Scholar] [CrossRef]
- Shalaby, R.; El-Hossainy, M.; Abo-Zalam, B.; Mahmoud, T.A. Optimal fractional-order PID controller based on fractional-order actor-critic algorithm. Neural Comput. Appl. 2022, 35, 2347–2380. [Google Scholar] [CrossRef]
- Vu, T.N.L.; Chuong, V.L.; Truong, N.T.N.; Jung, J.H. Analytical Design of Fractional-Order PI Controller for Parallel Cascade Control Systems. Appl. Sci. 2022, 12, 2222. [Google Scholar] [CrossRef]
- Skogestad, S.; Postlethwaithe, I. Multivariable Feedback Control Analysis and Design, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2001; pp. 253–351. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu-Batlle, V. Fractional-Order Systems and Controls, Fundamentals and Applications; Springer: London, UK, 2010. [Google Scholar]
- Choudhary, K.; Qureshi, M.S.; Singh, B. Position Control of DC Motor using Improved Sliding Mode Control Techniques. Int. J. Appl. Eng. Res. 2018, 13, 15–19. [Google Scholar]

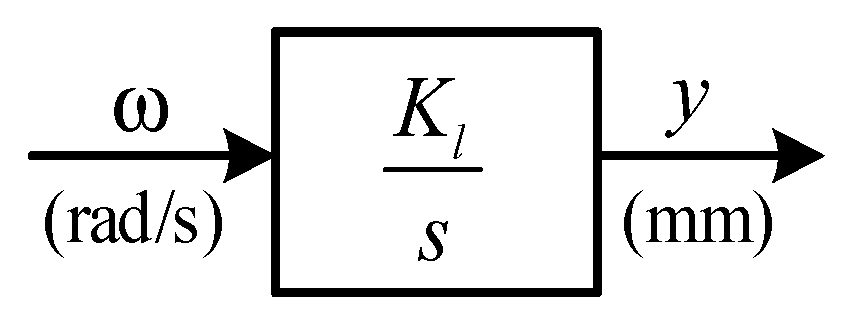



| Symbols | Values | Units |
|---|---|---|
| La | 8 × 10−5 | H |
| Ra | 0.316 | Ohm |
| Jm | 1.34 × 10−5 | kgm2 |
| b | 1.82 × 10−5 | Nm/rad/s |
| Km | 0.03 | Nm/A |
| Ke | 0.03 | V/rad/s |
| l | 0.01 | m |
| JL | 6.75 × 10−5 | kgm2 |
| DL | 1.82 × 10−4 | Nm/rad/s |
| Case 1 | Case 2 | |||||||
|---|---|---|---|---|---|---|---|---|
| IAE | ITAE | TV | µ (M) | IAE | ITAE | TV | µ (M) | |
| Nominal | 0.0515 | 0.0543 | 21.06 | 0.40 | 5.655 | 5.971 | 1.949 | 0.524 |
| Perturbed (±20%) | 0.0962 | 0.3693 | 18.63 | 0.42 | 8.801 | 29.883 | 1.543 | 0.5243 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chuong, V.L.; Nam, N.H.; Giang, L.H.; Vu, T.N.L. Robust Fractional-Order PI/PD Controllers for a Cascade Control Structure of Servo Systems. Fractal Fract. 2024, 8, 244. https://doi.org/10.3390/fractalfract8040244
Chuong VL, Nam NH, Giang LH, Vu TNL. Robust Fractional-Order PI/PD Controllers for a Cascade Control Structure of Servo Systems. Fractal and Fractional. 2024; 8(4):244. https://doi.org/10.3390/fractalfract8040244
Chicago/Turabian StyleChuong, Vo Lam, Ngo Hong Nam, Le Hieu Giang, and Truong Nguyen Luan Vu. 2024. "Robust Fractional-Order PI/PD Controllers for a Cascade Control Structure of Servo Systems" Fractal and Fractional 8, no. 4: 244. https://doi.org/10.3390/fractalfract8040244





