Modeling the 2013 Zika Outbreak in French Polynesia: Intervention Strategies
Abstract
:1. Introduction
2. Related Work
3. Methodology
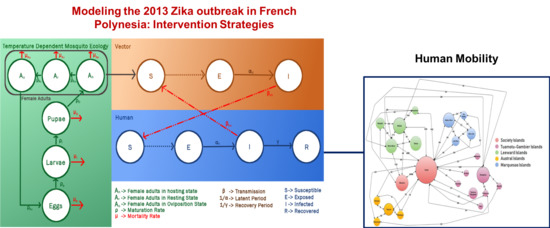
3.1. Mosquito Ecology
3.1.1. Variation with Temperature
3.1.2. Synthetic Mosquito Population
3.2. Mosquito Human Interaction (SEI-SEIR Model)
3.3. Transit Network
3.4. Basic Reproduction Number
Construction of NGM
- (1)
- Linearize the infected subsystem to get the Jacobian matrix, J.
- (2)
- Decompose the Jacobian matrix into T and , where T is the transmission part and is the transition part, such that . T represents the birth of new infections and represents all other transitions (recovery, mortality, etc.). is the rate at which individuals in state i give rise to individuals in state j and represents the time an individual in state j will spend in state i in their future life.
- (3)
- Compute K as
4. Experiments and Results
- Ratio of mosquito-human population (m): The ratio of mosquito-human population was used to estimate the initial vector population, such that total mosquito population is m times the total human population on each island. The base ratio was chosen as 3.
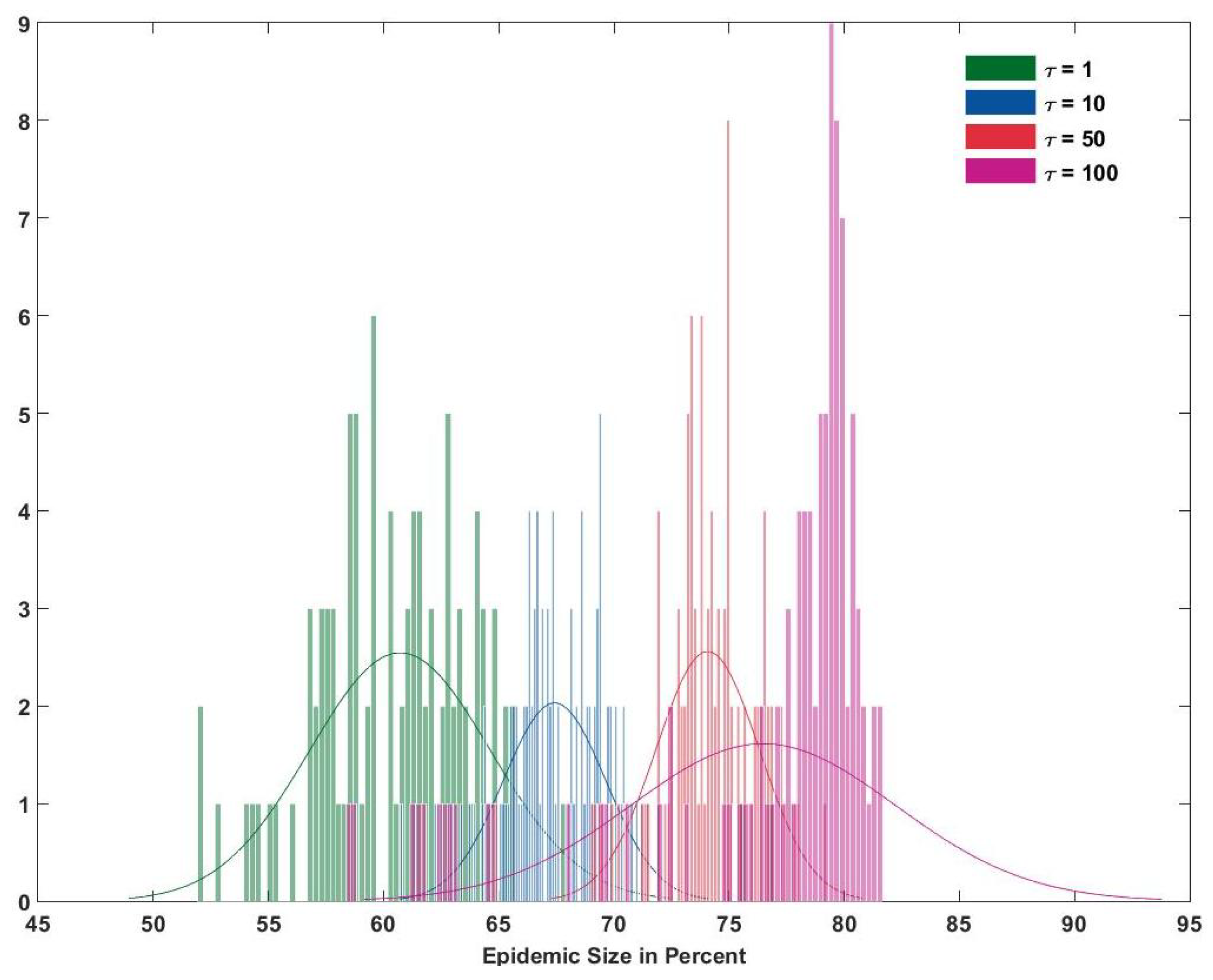
- Transit network load (load): The network shown in Figure 3 represents the daily average of the maximum passengers that travel from one island to another. Since all the flights or ferries may not be full everyday, the simulation was executed by changing the load from 1 (maximum) to {0.75, 0.50, 0.25, 0.10}.
4.1. Base Case and Validation
4.2. Intervention Strategies
4.2.1. Travel Bans/Advisories
4.2.2. Mosquito Control
4.2.3. Bite Prevention
5. Discussion
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- CDC. Zika Virus:Information for Clinicians. 2016. Available online: www.cdc.gov/zika (accessed on 3 August 2018).
- Ridler, C. CNS infections: Zika virus mutation associated with increased infectivity, mortality and severe microcephaly. Nat. Rev. Neurol. 2017. [Google Scholar] [CrossRef] [PubMed]
- Xia, H.; Luo, H.; Shan, C.; Muruato, A.E.; Nunes, B.T.D.; Medeiros, D.B.A.; Zou, J.; Xie, X.; Giraldo, M.I.; Vasconcelos, P.F.C.; et al. An evolutionary NS1 mutation enhances Zika virus evasion of host interferon induction. Nat. Commun. 2018, 9. [Google Scholar] [CrossRef] [PubMed]
- CDC. Dengue and Climate. 2012. Available online: www.cdc.gov (accessed on 1 December 2017).
- Musso, D. Zika Virus Transmission from French Polynesia to Brazil. Emerg. Infect. Dis. 2015, 21. [Google Scholar] [CrossRef] [PubMed]
- Kucharski, A.J.; Funk, S.; Eggo, R.M.; Mallet, H.P.; Edmund, W.J.; Nilles, E.J. Transmission Dynamics of Zika Virus in Island Populations: A Modelling Analysis of the 2013–14 French Polynesia Outbreak. PLos Negl. Trop. Dis. 2016, 10. [Google Scholar] [CrossRef] [PubMed]
- Riou, J.; Poletto, C.; Boëlle, P. A comparative analysis of Chikungunya and Zika transmission. Epidemics 2017, 19, 43–52. [Google Scholar] [CrossRef] [PubMed]
- Hyer, R.; Covello, V. Top Questions on Zika: Simple Answers; Association of State, and Territorial Health Officials: Arlington, VA, USA, 2017. [Google Scholar]
- Osuna, C.E.; Lim, S.; Deleage, C.; Griffin, B.D.; Stein, D. Zika viral dynamics and shedding in rhesus and cynomolgus macaques. Nat. Med. 2016, 22, 1448–1455. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, D.; Lou, Y.; He, D. Prevention and Control of Zika as a Mosquito-Borne and Sexually Transmitted Disease: A Mathematical Modeling Analysis. Nat. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Ciota, A.T.; Bialosuknia, S.M.; Ehrbar, D.J.; Kramer, L.D. Vertical Transmission of Zika Virus by Aedes aegypti and Ae. albopictus Mosquitoes. Emerg. Infect. Dis. 2017, 23, 880–882. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nelms, B.M.; Fechter-Leggett, E.; Carroll, B.D.; Macedo, P.; Kluh, S.; Reisen, W.K. Experimental and natural vertical transmission of West Nile virus by California Culex (Diptera: Culicidae) mosquitoes. J. Med. Entomol. 2013, 50, 371–378. [Google Scholar] [CrossRef] [PubMed]
- Rosen, L.; Shroyer, D.A.; Tesh, R.B.; Freier, J.E.; Lien, J.C. Transovarial transmission of dengue viruses by mosquitoes: Aedes albopictus and Aedes aegypti. Am. J. Trop. Med. Hyg. 1983, 32, 1108–1119. [Google Scholar] [CrossRef] [PubMed]
- Bakach, I. A Survey of Mathematical Models of Dengue Fever. Ph.D. Thesis, Department of Mathematics, The University of Iowa, Iowa City, IA, USA, 2015. [Google Scholar]
- Apolloni, A.; Poletto, C.; Colizza, V. Age-specific contacts and travel patterns in the spatial spread of 2009 h1n1 influenza pandemic. BMC Infect. Dis. 2013, 13. [Google Scholar] [CrossRef] [PubMed]
- Hollingsworth, T.D.; Ferguson, N.M.; Anderson, R.M. Frequent travelers and rate of spread of epidemics. Emerg. Infect. Dis. 2007, 13. [Google Scholar] [CrossRef] [PubMed]
- Liu-Helmersson, J.; Stenlund, H.; Wilder-Smith, A.; Rocklöv, J. Vectorial Capacity of Aedes aegypti: Effects of Temperature and Implications for Global Dengue Epidemic Potential. PLoS ONE 2014, 9, e0089783. [Google Scholar] [CrossRef] [PubMed]
- Vaidya, A.; Mikler, A.R.; Bravo-Salgado, A.D. Modeling climate-dependent population dynamics of mosquitoes to guide public health policies. In Proceedings of the 5th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics, Newport Beach, CA, USA, 20–23 September 2014; pp. 380–389. [Google Scholar] [CrossRef]
- Adams, B.; Kapan, D.D. Man bites mosquito: Understanding the contribution of human movement to vector-borne disease dynamics. PLoS ONE 2009, 4, e0006763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lutambi, A.M.; Penny, M.A.; Smith, T.; Chitnis, N. Mathematical modelling of mosquito dispersal in a heterogeneous environment. Math. Biosci. 2013, 241, 198–216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ewing, D.A.; Cobbold, C.A.; Purse, B.V.; Nunn, M.A.; White, S.M. Modelling the effect of temperature on the seasonal population dynamics of temperate mosquitoes. J. Theor. Biol. 2016, 400, 65–79. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lounibos, L.P.; Escher, R.L. Sex ratios of mosquitoes from long-term censuses of florida tree holes. J. Am. Mosq. Control Assoc. 2008, 24, 11–15. [Google Scholar] [CrossRef] [PubMed]
- Beserra, E.B.; de Castro, F.P., Jr.; dos Santos, J.W.; Santos, T.; Fernandes, C.R.M. Biologia e Exigências Térmicas de Aedes aegypti (L.) (Diptera:Culicidae) Provenientes de Quatro Regiões Bioclimáticas da Paraíba. Neotrop. Entomol. 2006, 35, 853–860. [Google Scholar] [CrossRef] [PubMed]
- Otero, M.; Solari, H.G.; Schweigmann, N. A stochastic population dynamics model for Aedes aegypti: formulation and application to a city with temperate climate. Bull. Math. Biol. 2006, 68. [Google Scholar] [CrossRef] [PubMed]
- Rueda, L.M.; Patel, K.J.; Axtell, R.C.; Stinner, R.E. Temperature-dependent development and survival rates of culex quinquefasciatus and aedes aegypti (diptera: Culicidae). J. Med. Entomol. 1990, 27, 892–898. [Google Scholar] [CrossRef] [PubMed]
- The weather company LLC. Weather History for Tahiti, French Polynesia. 2017. Available online: https://www.wunderground.com/history (accessed on 25 July 2017).
- Fages, J.; Robineau, C. French Polynesia. World Atlas of Agriculture, Verona: Centro di Geografia Agraria 1972, 9, 613. [Google Scholar]
- Caminade, C.; Turnera, J.; Metelmann, S. Global risk model for vector-borne transmission of Zika virus reveals the role of El Niño 2015. PNAS 2016, 114. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Suna, K.; Chinazzia, M.; Piontti, A.P. Spread of Zika virus in the Americas: Supporting Information. PNAS 2017, 114. [Google Scholar] [CrossRef] [PubMed]
- Derouich, M.; Boutayeb, A.; Twizell, E.H. A model of dengue fever. BioMed. Eng. OnLine 2003, 2. [Google Scholar] [CrossRef]
- Musso, D.; Gubler, D.J. Zika Virus. Clin. Microbiol. Rev. 2016, 29, 487–524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Statistical Institute of French Polynesia (SISPF). Population by Geography Archipelagos / Islands and by Ten-Year Age. 2015. Available online: www.ispf.pf/bases/Recensements/2012/Donnees_detaillees/Population.aspx (accessed on 3 August 2018).
- AirTahiti. Flying in an ATR. 2016. Available online: www.airtahiti.com/fleet-atr (accessed on 20 March 2017).
- Heffernan, J.M.; Smith, R.J.; Wahl, L.M. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2005, 2. [Google Scholar] [CrossRef] [PubMed]
- Deikmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Deikmann, O.; Heesterbeek, J.A.P.; Roberts, M.G. On the definition and the computation of the basic reproduction ratio r0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990, 28, 365–383. [Google Scholar] [CrossRef]
- Deikmann, O.; Heesterbeek, J.A.P. Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation; John Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Centre d’hygiene et de salubrite publique. Surveillance de la dengue et du zika en Polynésie française. 2014. Available online: www.hygiene-publique.gov.pf (accessed on 7 July 2017).
- Johnson, T.V.; Mikler, A.R. Chasing r0: Understanding the effects of population dynamics on the basic reproduction number. J. Biol. Syst. 2011, 19. [Google Scholar] [CrossRef]
- Champagne, C.; Salthouse, D.G.; Paul, R.; Cao-Lormeau, V.; Roche, B.; Cazelles, B. Structure in the variability of the basic reproductive number (R0) for Zika epidemics in the Pacific islands. eLife 2016, 5. [Google Scholar] [CrossRef] [PubMed]
- Nishiura, H.; Mizumoto, K.; Villamil-Gómez, W.E.; Rodríguez-Morales, A.J. Preliminary estimation of the basic reproduction number of Zika virus infection during Colombia epidemic, 2015–2016. Travel Med. Infect. Dis. 2016, 14, 274–276. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Towers, S.; Brauer, F.; Castillo-Chaveza, C.; Falconar, A.K.I. Estimate of the reproduction number of the 2015 Zika virus outbreak in Barranquilla, Colombia, and estimation of the relative role of sexual transmission. Epidemics 2016, 17, 50–55. [Google Scholar] [CrossRef] [PubMed]









| Parameter | Symbol | Type | Value |
|---|---|---|---|
| Number of eggs laid per oviposition | b | Ranged | random (50–300) [20] |
| Oviposition Rate | Ranged | random (3.0–4.0) [20] | |
| Egg Mortality Rate | Regression | ||
| Egg Maturation Rate | Regression | ||
| Density Independent Larvae Mortality Rate | Ranged | random (0.32–0.80) [20] | |
| Density Dependent Larvae Mortality Rate | Constant | 0.05 [20] | |
| Larva Maturation Rate | Regression | ||
| Pupa Mortality Rate | Ranged | random (0.33–1.0) [20] | |
| Pupa Maturation Rate | Regression | ||
| Adult Mortality Rate (Hosting stage) | Ranged | random (0.322–0.598) [20] | |
| Adult Maturation Rate (Hosting stage) | Ranged | random (0.322–0.598) [20] | |
| Adult Maturation Rate (Resting stage) | Ranged | random (0.30–0.56) [20] | |
| Adult Mortality Rate (Resting stage) | Ranged | random (0.0034–0.01) citemosquitomodel | |
| Adult Mortality Rate (Oviposition stage) | Ranged | random (0.41–0.56) [20] |
| Parameter | Value |
|---|---|
| Transmission Probability (human to vector), | Temperature dependent [17] |
| Transmission Probability (vector to human), | Temperature dependent [17] |
| Bite Rate of susceptible mosquitoes(in bites per day), | Temperature dependent [17] |
| Bite Rate of infectious mosquitoes(in bites per day), | 2 [30] |
| Latent Period for humans(in days), | random (3–15) [1] |
| Recovery Period for humans(in days), | 7 [1] |
| Latent Period for mosquitoes(in days), | 15 [31] |
| Island | Admin Division | Population |
|---|---|---|
| Tahiti* | Windward Islands | 183,480 |
| Moorea | Windward Islands | 16,899 |
| Bora Bora | Leeward Islands | 9596 |
| Raitea* | Leeward Islands | 12,237 |
| Tahaa | Leeward Islands | 5220 |
| Huahine | Leeward Islands | 6303 |
| Maupiti | Leeward Islands | 1194 |
| Nuku Hiva* | Marquesas Islands | 2967 |
| Ua Huka | Marquesas Islands | 621 |
| Ua Pou | Marquesas Islands | 2175 |
| Hiva Oa | Marquesas Islands | 2184 |
| Arutua | Tuamotu Gambier Islands | 680 |
| Rangiroa* | Tuamotu Gambier Islands | 2567 |
| Manihi | Tuamotu Gambier Islands | 685 |
| Fakarava | Tuamotu Gambier Islands | 806 |
| Hao | Tuamotu Gambier Islands | 1066 |
| Makemo | Tuamotu Gambier Islands | 832 |
| Takaroa-Takapoto | Tuamotu Gambier Islands | 1262 |
| Gambier | Tuamotu Gambier Islands | 1239 |
| Tupuai* | Austral Islands | 2170 |
| Rimatara | Austral Islands | 873 |
| Rurutu | Austral Islands | 2322 |
| Raivavae | Austral Islands | 940 |
| Place | Reporting Rate [7] | Calculated Cases (Reported, CI-95%) | Reported Cases in [7] |
|---|---|---|---|
| Tahiti | 12% | 19,098 (19,022–19,175) | 21,406 |
| Moorea | 8% | 1156 (1150–1161) | 1235 |
| Austral Islands | 17% | 933 (920–946) | 1208 |
| Leeward Islands | 12% | 3517 (3473–3562) | 3912 |
| Marquesas Islands | 11% | 750 (738–762) | 994 |
| Tuamotu Gambier Islands | 8% | 641 (630–653) | 1211 |
| Total | 26,095 (25,933–26,259) | 29,966 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gwalani, H.; Hawamdeh, F.; Mikler, A.R.; Xiong, K. Modeling the 2013 Zika Outbreak in French Polynesia: Intervention Strategies. Appl. Syst. Innov. 2018, 1, 31. https://doi.org/10.3390/asi1030031
Gwalani H, Hawamdeh F, Mikler AR, Xiong K. Modeling the 2013 Zika Outbreak in French Polynesia: Intervention Strategies. Applied System Innovation. 2018; 1(3):31. https://doi.org/10.3390/asi1030031
Chicago/Turabian StyleGwalani, Harsha, Faris Hawamdeh, Armin R. Mikler, and Katherine Xiong. 2018. "Modeling the 2013 Zika Outbreak in French Polynesia: Intervention Strategies" Applied System Innovation 1, no. 3: 31. https://doi.org/10.3390/asi1030031