Micro-Vibration Analysis, Suppression, and Isolation of Spacecraft Flywheel Rotor Systems: A Review
Abstract
:1. Introduction
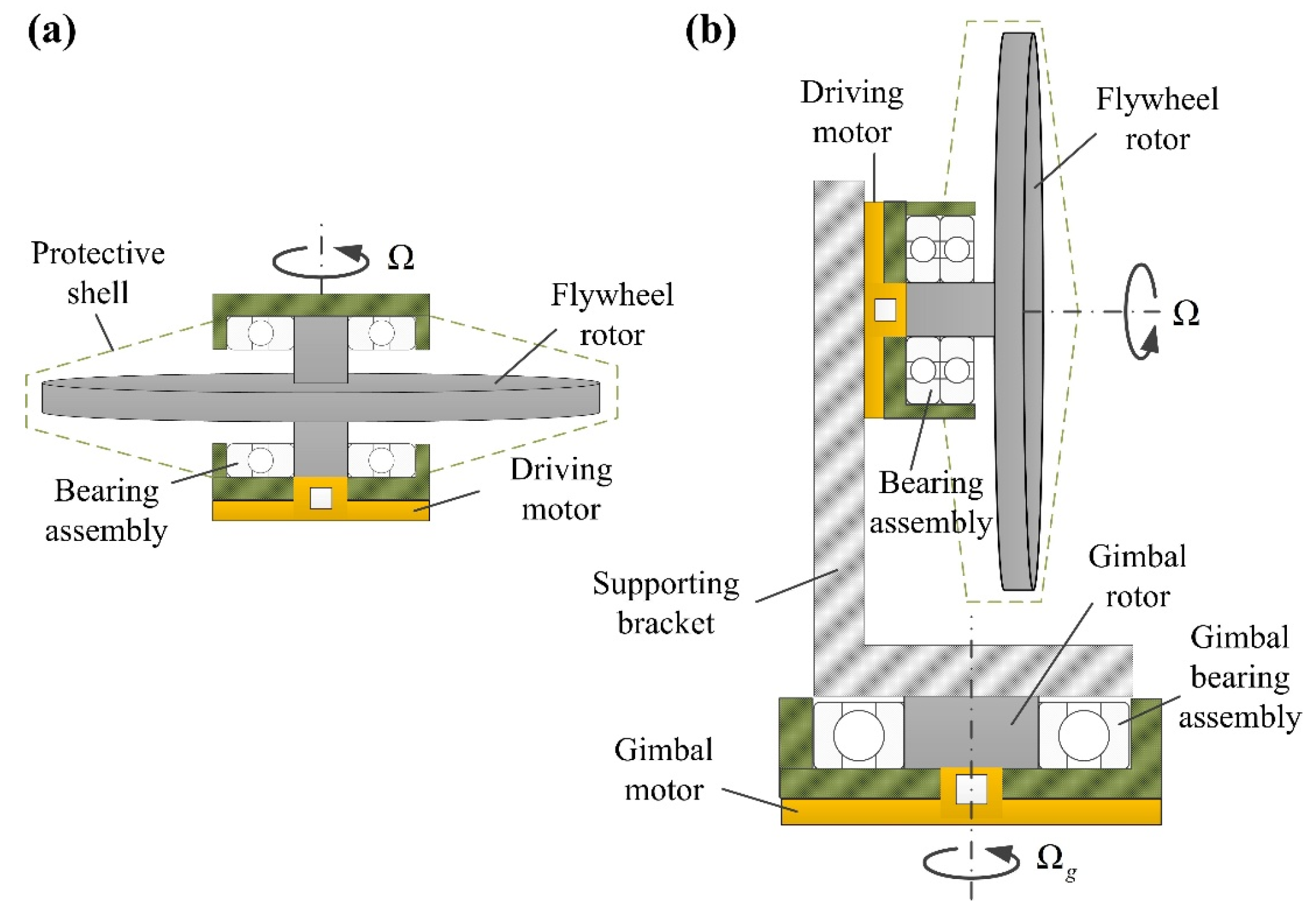
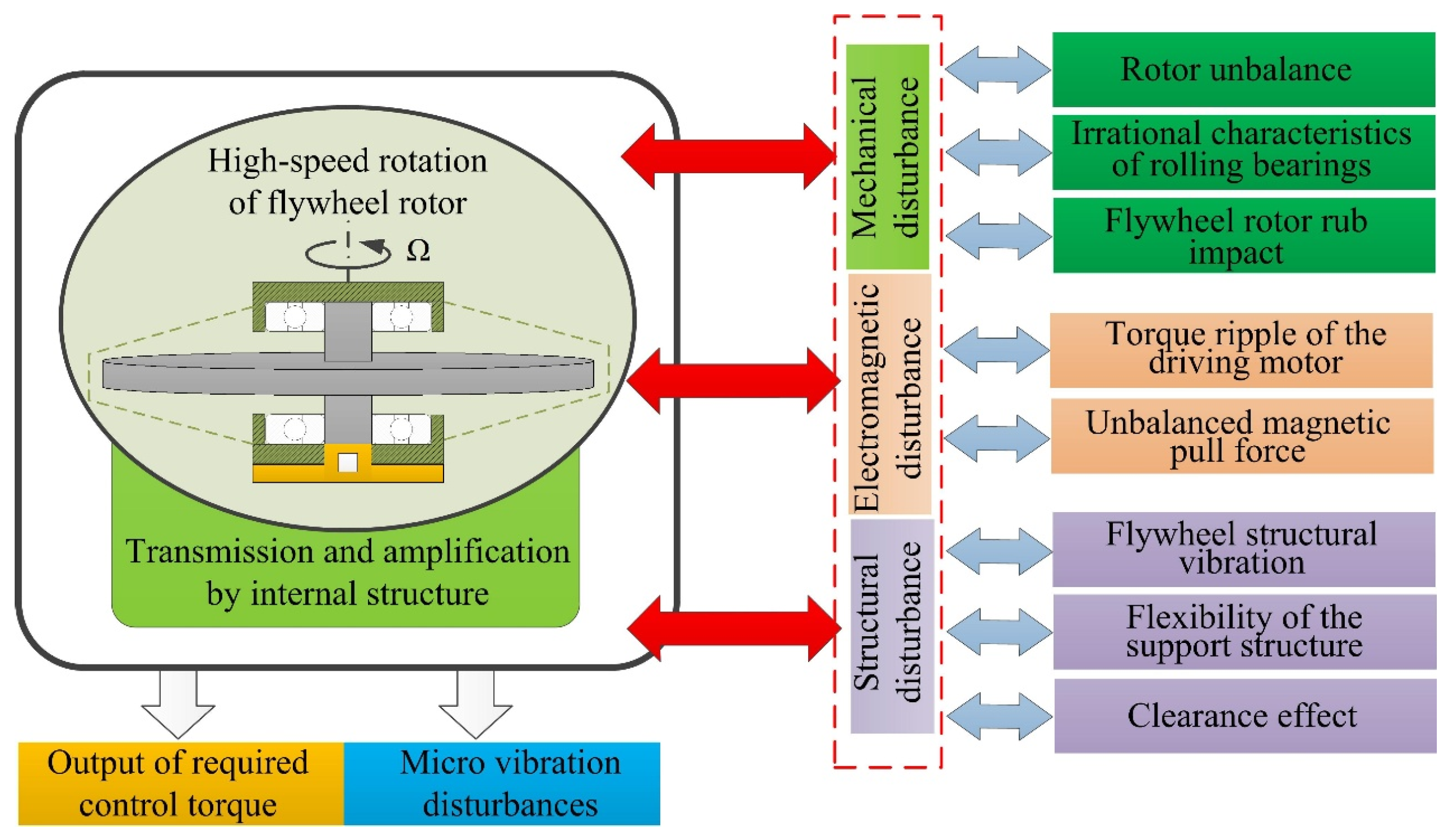
2. Disturbance Sources of Micro Vibration of SFRSs
2.1. Mechanical Disturbance
2.2. Electromagnetic Disturbance
2.3. Structural Disturbance
3. Micro Vibration Models of SFRSs
3.1. Empirical Models
3.2. Analytical Models
3.3. Hybrid Models
4. Micro-Vibration Suppression of SFRSs
4.1. Low Disturbance Flywheel Technology
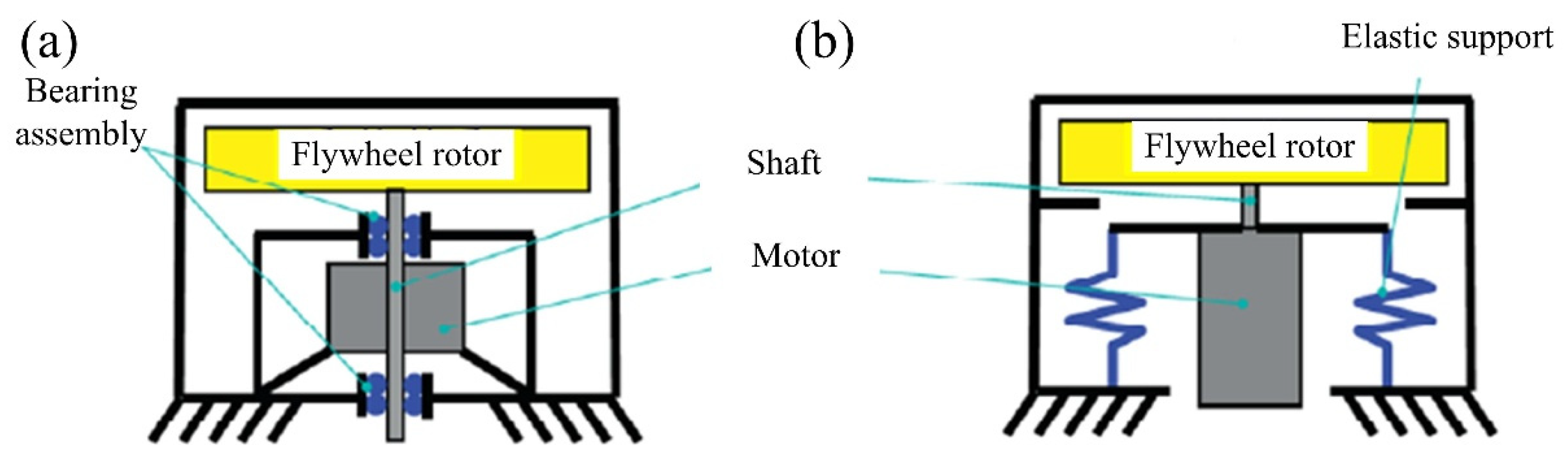
4.2. Elastic Supports
4.3. Maglev Bearing
5. Micro-Vibration Isolation of SFRSs
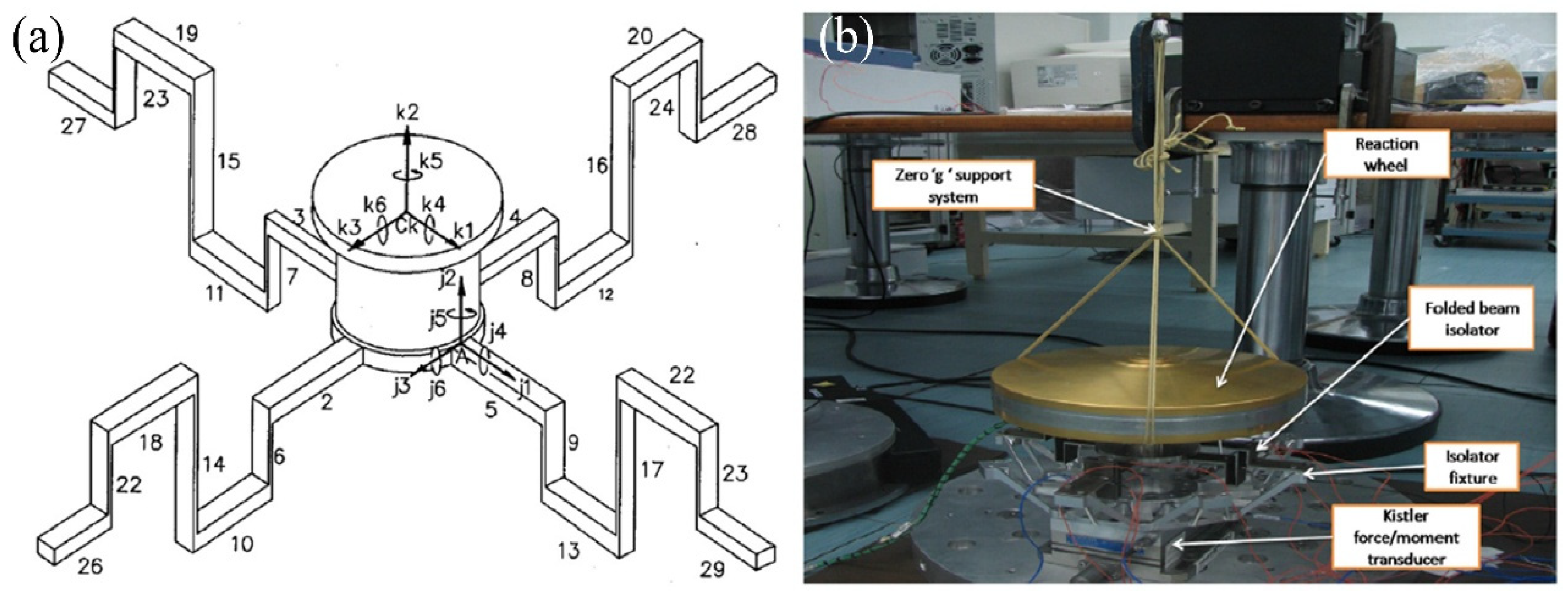
5.1. Micro-Vibration Isolation Based on a Folded Beam Structure
5.2. Micro-Vibration Isolation Based on Rod Elements
5.2.1. Unidirectional Platform
5.2.2. Three-Leg Platform
5.2.3. Six-Leg Platform
5.2.4. Eight-Leg Platform
5.3. Micro-Vibration Isolation Based on Maglev Technology
5.4. Micro-Vibration Isolation Using Nonlinear Factors
6. Micro-Vibration Measurement Technology on the Ground
6.1. Disturbance Force Measurement
6.2. Structural Acceleration Measurement
6.3. Structural Displacement Measurement
6.4. Micro-Vibration Simulator
7. Existing Problems and Future Research Directions
7.1. Micro-Vibration Models of SFRSs
7.2. Micro-Vibration Suppression of SFRSs
7.3. Micro-Vibration Isolation of SFRSs
7.4. Micro-Vibration Measurement Technology on the Ground
8. Conclusions and Prospects
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Jiang, J.; Zhang, G.; Lu, Y. High-accuracy location algorithm of planetary centers for spacecraft autonomous optical navigation. Acta Astronaut. 2019, 161, 542–551. [Google Scholar] [CrossRef]
- Akhmetov, R.; Eremeev, V.; Kuznecov, A.; Myatov, G.; Poshekhonov, V.; Stratilatov, N. High-precision geolocation of earth surface images from the resurs-p spacecraft. Izv. Atmos. Ocean. Phys. 2017, 53, 1155–1163. [Google Scholar] [CrossRef]
- Pong, C. High-Precision Pointing and Attitude Estimation and Control Algorithms for Hardware-Constrained Spacecraft; Massachusetts Institute of Technology: Cambridge, MA, USA, 2014. [Google Scholar]
- Lee, D.; Vukovich, G.; Lee, R. Robust adaptive unscented Kalman filter for spacecraft attitude estimation using quaternion measurements. J. Aerosp. Eng. 2017, 30, 04017009. [Google Scholar] [CrossRef]
- Liu, C.; Ye, D.; Shi, K.; Sun, Z. Robust high-precision attitude control for flexible spacecraft with improved mixed control strategy under poles assignment constraint. Acta Astronaut. 2017, 136, 166–175. [Google Scholar] [CrossRef]
- Marshall, T.; Gunderman, T.; Mobley, F. Reaction wheel control of the MSX satellite. In Proceedings of the Annual Rocky Mountain Guidance and Control Conference, San Diego, CA, USA, 2–6 February 1991. [Google Scholar]
- Zhang, R. Satellite Orbit Attitude Dynamics and Control; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 1998. (In Chinese) [Google Scholar]
- Miller, D.; Weck, O.; Uebelhart, S.; Grogan, R.; Basdogan, I. Integrated dynamics and controls modeling for the space interferometry mission. In Proceedings of the IEEE Aerospace Conference Proceedings, Big Sky, MT, USA, 10–17 March 2001. [Google Scholar]
- Miller, S.E.; Kirchman, P.; Sudey, J. Reaction wheel operational impacts on the goes jitter environment. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007. [Google Scholar]
- Kim, Y.K.; Koo, J.H.; Kim, K.S. Vibration isolation strategies using magneto-rheological elastomer for a miniature cryogenic cooler in space application. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Montreal, QC, Canada, 6–9 July 2010; pp. 1203–1206. [Google Scholar]
- Pong, C.M.; Smith, M.W.; Knutson, M.W. One-arcsecond line-of-sight pointing control on exoplanetsat, a three-unit cubesat. Adv. Astronaut. Sci. 2011, 141, 11–35. [Google Scholar]
- Iyer, A.; Singh, S.N. Non-linear momentum and attitude control of a space station accommodating periodic aerodynamic disturbance. Acta Astronaut. 1995, 35, 391–402. [Google Scholar] [CrossRef]
- Qu, Y.; Lu, C.; Li, T.; Yin, H. Research status and development prospect of high resolution satellite micro vibration. Aerosp. China 2014, 8, 22–24. (In Chinese) [Google Scholar]
- Davis, L.; Wilson, J.; Jewell, R. Hubble Space Telescope Reaction Wheel Assembly Vibration Isolation System; NASA Marshall Space Flight Center: Huntsville, AL, USA, 1986.
- Hyde, T.; Davis, L. Vibration Reduction for Commercial Optical Inter-Satellite Communication Links; SPIE Conference on Smart Structures and Integrated Systems: San Diego, CA, USA, 1998; pp. 94–105. [Google Scholar]
- Lee, A.; Yu, J.; Kahn, P. Space interferometry mission spacecraft pointing error budgets. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 502–514. [Google Scholar] [CrossRef]
- Watkins, R.; Agrawal, B.; Shin, Y.; Chen, H. Jitter control of space and airborne laser beams. In Proceedings of the 22nd AIAA International Communications Satellite Systems Conference & Exhibit, Monterey, CA, USA, 9–12 May 2004. [Google Scholar]
- Masterson, R.A.; Miller, D.W. Development and validation of empirical and analytical reaction wheel disturbance models. In Proceedings of the AIAA/ASME/ASCE/AHS/ASC Structures. Structural Dynamics and Materials Conference, St. Louis, MO, USA, 12–15 April 1999; pp. 1–10. [Google Scholar]
- Bialke, B. High fidelity mathematical modeling of reaction wheel performance. Adv. Astronaut. Sci. 1998, 98, 483–496. [Google Scholar]
- Yang, X.; Chang, L.; Jin, G. Influence of dynamic imbalance of SGCMG rotor on remote sensing satellite imaging. Chin. Opt. 2012, 5, 358–365. [Google Scholar]
- Genta, G. Dynamics of Rotating Systems; Springer Science+Business Media, Inc.: New York, NY, USA, 2004. [Google Scholar]
- Wensing, J.A. On the Dynamics of Ball Bearings; University of Twente: Enschede, The Netherlands, 1998. [Google Scholar]
- Tallian, T.E.; Gustafsson, O.G. Progress in rolling bearing vibration research and control. Trans. ASLE Tribol. Trans. 1965, 8, 195–207. [Google Scholar] [CrossRef]
- Jang, G.H.; Jeong, S.W. Nonlinear excitation model of ball bearing waviness in a rigid rotor supported by two or more ball bearings considering five degrees of freedom. Trans. ASME J. Tribol. 2002, 124, 82–90. [Google Scholar] [CrossRef]
- Jang, G.H.; Jeong, S.W. Vibration analysis of a rotating system due to the effect of ball bearing waviness. J. Sound Vib. 2004, 269, 709–726. [Google Scholar] [CrossRef]
- Bai, C.Q.; Xu, Q.Y. Dynamic model of ball bearings with internal clearance and waviness. J. Sound Vib. 2006, 294, 23–48. [Google Scholar]
- Babu, C.K.; Tandon, N.; Pandey, R.K. Vibration modelling of a rigid rotor supported on the lubricated angular contact ball bearings considering six degrees of freedom and waviness on balls and races. Trans. ASME J. Vib. Acoust. 2012, 134, 1–12. [Google Scholar] [CrossRef]
- Wang, L.Q.; Cui, L.; Zheng, D.Z. Nonlinear dynamics behaviors of a rotor roller bearing system with radial clearances and waviness considered. Chin. J. Aeronaut. 2007, 21, 86–96. [Google Scholar]
- Cao, M.; Xiao, J. A comprehensive dynamic model of double-row spherical roller bearing: Model development and case studies on surface defects, preloads, and radial clearance. Mech. Syst. Signal Process. 2008, 22, 467–489. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Q.; Peng, Z.; Chu, F. A new nonlinear dynamic model of the rotor-bearing system considering preload and varying contact angle of the bearing. Commun. Nonlinear Sci. Numer. Simul. 2015, 22, 821–841. [Google Scholar] [CrossRef]
- Han, Q.; Chu, F. Nonlinear dynamic model for skidding behavior of angular contact ball bearings. J. Sound Vib. 2015, 354, 219–235. [Google Scholar] [CrossRef]
- Randall, R.; Antoni, J.; Clapp, B. Rolling element bearing diagnostics: A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Jin, L.; Xu, S. Dynamic modeling and low rate control of gimbal servo system for single gimbal control moment gyro. Chin. Space Sci. Technol. 2010, 12, 1–10. [Google Scholar]
- Muszynska, A. Rotor to stationary element rub-related vibration phenomena in rotating machinery-literature survey. Shock Vib. Dig. 1989, 21, 3–11. [Google Scholar] [CrossRef]
- Chu, F.; Lu, W. Experimental observation of nonlinear vibrations in a rub-impact rotor system. J. Sound Vib. 2005, 283, 621–643. [Google Scholar] [CrossRef]
- Chu, F.; Lu, W. Stiffening effect of the rotor during the rotor-to-stator rub in a rotating machine. J. Sound Vib. 2007, 308, 758–766. [Google Scholar] [CrossRef]
- Pennachi, P.; Bachschmid, N.; Tanzi, E. Light and short arc rubs in rotating machines: Experimental tests and modeling. Mech. Syst. Signal Process. 2009, 23, 2205–2227. [Google Scholar] [CrossRef]
- Jacquet-Richardet, G.; Torkhani, M.; Cartraud, P. Rotor to stator contacts in turbomachines: Review and application. Mech. Syst. Signal Process. 2013, 40, 401–420. [Google Scholar] [CrossRef]
- Ma, H.; Yin, F.L.; Guo, Y.Z. A review on dynamic characteristics of blade-casing rubbing. Nonlinear Dyn. 2016, 84, 437–472. [Google Scholar] [CrossRef]
- Wie, B.; Bailey, D.; Heiberg, C. Singularity robust steering logic for redundant single-gimbal control moment gyros. J. Guid. Control Dyn. 2001, 24, 865–872. [Google Scholar] [CrossRef]
- Gustavsson, R.; Aidanpaa, J. The influence of nonlinear magnetic pull on hydropower generator rotors. J. Sound Vib. 2006, 297, 551–562. [Google Scholar] [CrossRef]
- Lundstrom, N.; Aidanpaa, J. Dynamic consequences of electromagnetic pull due to derivations in generator shape. J. Sound Vib. 2007, 301, 207–225. [Google Scholar] [CrossRef]
- Akiyama, Y. Unbalanced heating phenomenon of induction motor with eccentric rotor. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Huston, TX, USA, 4–9 October 1992; pp. 107–114. [Google Scholar]
- Dorrell, D. Sources and characteristics of unbalanced magnetic pull in three-phase cage induction motors with axial-varying rotor eccentricity. IEEE Trans. Ind. Appl. 2011, 47, 12–24. [Google Scholar] [CrossRef]
- Zhu, Z.Q.; Mohd-Jamil, M.; Wu, L. Influence of slot and pole number combinations on unbalanced magnetic force in PM machines with diametrically asymmetric windings. IEEE Trans. Ind. Appl. 2013, 49, 19–30. [Google Scholar] [CrossRef]
- Xu, X.; Han, Q.; Chu, F. A four degrees-of-freedom model for a misaligned electrical rotor. J. Sound Vib. 2015, 358, 356–374. [Google Scholar] [CrossRef]
- Xu, X.; Han, Q.; Chu, F. Nonlinear vibration of a generator rotor with unbalanced magnetic pull considering both dynamic and static eccentricities. Arch. Appl. Mech. 2016, 86, 1521–1536. [Google Scholar] [CrossRef]
- Xu, X.; Han, Q.; Chu, F. A general electromagnetic excitation model for electrical machines considering the magnetic saturation and rub impact. J. Sound Vib. 2018, 416, 154–171. [Google Scholar] [CrossRef]
- Friswell, M.; Penny, J.; Garvey, S.; Lees, A. Dynamics of Rotating Machines; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Harris, T.A.; Kotzalas, M.N. Rolling Bearing Analysis; Taylor & Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
- Zhang, X.; Han, Q.; Peng, Z.; Chu, F. Stability analysis of a rotor-bearing system with time-varying bearing stiffness due to finite number of balls and unbalanced force. J. Sound Vib. 2013, 332, 6768–6784. [Google Scholar] [CrossRef]
- Zhang, X.; Han, Q.; Peng, Z.; Chu, F. A comprehensive dynamic model to investigate the stability problems of the rotor-bearing system due to multiple excitations. Mech. Syst. Signal Process. 2016, 70, 1171–1192. [Google Scholar] [CrossRef]
- Harsha, M. Reaction Wheel Mechanical Noise Variations. Space Telesc. Program Eng. Memo SSS 1986, 218, 175–183. [Google Scholar]
- Masterson, R.; Miller, D.; Grogan, R. Development and validation of reaction wheel disturbance models: Empirical model. J. Sound Vib. 2002, 249, 575–598. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, J.; Tian, H. Development of methods identifying parameters in reaction wheel assembly disturbance model. Aircr. Eng. Aerosp. Technol. 2006, 78, 326–330. [Google Scholar] [CrossRef]
- Bai, Z.; Zhao, Y.; Ma, W.; Wang, Y. Effects analysis of reaction wheel disturbance on structure dynamics characters of spacecraft. J. Astronaut. 2009, 30, 2073–2079. [Google Scholar]
- Yin, X.; Xu, Y.; Sheng, X.; Shen, Y. Signal denoising method using AIC-SVD and its application to micro-vibration in reaction wheels. Sensors 2019, 19, 5032. [Google Scholar] [CrossRef]
- Shields, J.; Pong, C.; Lo, K.; Jones, L.; Mohan, S.; Marom, C.; McKinley, I.; Wilson, W.; Andrade, L. Characterization of cubesat reaction wheel assemblies. J. Small Satell. 2017, 6, 565–580. [Google Scholar]
- Elias, L.; Miller, D. A coupled disturbances analysis method using dynamic mass measurement techniques. In Proceedings of the AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Denver, CO, USA, 22–25 April 2002; p. 1252. [Google Scholar]
- Elias, L.; Dekens, F.; Basdogan, I.; Sievers, L.; Neville, T. A methodology for modeling the mechanical interaction between a reaction wheel and a flexible structure. In Proceedings of the SPIE 4852, Interferometry in Space, Waikoloa, HI, USA, 26 February 2003. [Google Scholar]
- Shigemune, T.; Yoshiaki, O. Experimental and numerical analysis of reaction wheel disturbances. JSME Int. J. 2003, 46, 519–526. [Google Scholar]
- Xia, M.; Qin, C.; Wang, X.; Xu, Z. Modeling and experimental study of dynamic characteristics of the moment wheel assembly based on structural coupling. Mech. Syst. Signal Process. 2021, 146, 107007. [Google Scholar] [CrossRef]
- Huang, L.; Wu, Z.; Wang, K. High-precision anti-disturbance gimbal servo control for control moment gyroscopes via an extended harmonic disturbance observer. IEEE Access 2018, 6, 66336–66349. [Google Scholar] [CrossRef]
- Huang, L.; Wu, Z.; Wang, K. Indirect measurement of rotor dynamic imbalance for control moment gyroscopes via gimbal disturbance observer. Sensors 2018, 18, 1873. [Google Scholar] [CrossRef] [PubMed]
- Masterson, R. Development and Validation of Empirical and Analytical Reaction Wheel Disturbance Models; Massachusetts Institute of Technology: Cambridge, MA, USA, 1999. [Google Scholar]
- Li, L.; Dai, J. Inner disturbance modeling and simulation analysis of reaction wheel system. J. Syst. Simul. 2005, 17, 1855–1859. [Google Scholar]
- Deng, R.; Hu, G.; Wang, Q. Whirling characteristics of high speed rotors in flywheel and CMG. Aerosp. Control Appl. 2009, 35, 56–60. [Google Scholar]
- Zhang, Z.; Aglietti, G.; Zhou, W. Microvibrations induced by a cantilevered wheel assembly with a soft-suspension system. AIAA J. 2011, 49, 1067–1079. [Google Scholar] [CrossRef]
- Zhou, W.; Aglietti, G.; Zhang, Z. Modelling and testing of a soft suspension design for a reaction/momentum wheel assembly. J. Sound Vib. 2011, 330, 4596–4610. [Google Scholar] [CrossRef]
- Zhang, Z.; Aglietti, G.; Ren, W. Microvibration model development and validation of a cantilevered reaction wheel assembly. Appl. Mech. Mater. 2012, 226–228, 133–137. [Google Scholar] [CrossRef]
- Zhang, Z.; Aglietti, G.; Ren, W. Coupled microvibration analysis of a reaction wheel assembly including gyroscopic effects in its accelerance. J. Sound Vib. 2013, 332, 5748–5765. [Google Scholar] [CrossRef]
- Addari, D.; Aglietti, G.; Remedia, M. Experimental and numerical investigation of coupled microvibration dynamics for satellite reaction wheels. J. Sound Vib. 2017, 386, 225–241. [Google Scholar] [CrossRef]
- Addari, D.; Aglietti, G.; Remedia, M. Dynamic mass of a reaction wheel including gyroscopic effects: An experimental approach. AIAA J. 2017, 55, 274–285. [Google Scholar] [CrossRef]
- Peng, C.; Fang, J.; Cui, P. Dynamics modeling and measurement of the microvibrations for a magnetically suspended flywheel. IEEE Trans. Instrum. Meas. 2015, 64, 3239–3252. [Google Scholar] [CrossRef]
- Luo, Q.; Li, D.; Zhou, W. Studies on vibration isolation for a multiple flywheel system in variable configurations. J. Vib. Control 2015, 21, 105–123. [Google Scholar] [CrossRef]
- Wan, Q.; Liu, G.; Shi, H.; Zhang, X.; Ning, X. Analysis of dynamic characteristics for momentum wheel assembly with joint clearance. Adv. Mech. Eng. 2018, 10, 1687814018818919. [Google Scholar] [CrossRef]
- Chou, M.; Liaw, C. Dynamic control and diagnostic friction estimation for an SPMSM-driven satellite reaction wheel. IEEE Trans. Ind. Electron. 2011, 58, 4693–4707. [Google Scholar] [CrossRef]
- Alcorn, J.; Allard, C.; Schaub, H. Fully coupled reaction wheel static and dynamic imbalance for spacecraft jitter modeling. J. Guid. Control Dyn. 2018, 41, 1380–1388. [Google Scholar] [CrossRef]
- Wang, H.; Chen, L.; Jin, Z.; Crassidis, J. Adaptive momentum distribution jitter control for microsatellite. J. Guid. Control Dyn. 2019, 42, 632–641. [Google Scholar] [CrossRef]
- Aghalari, A.; Shahravi, M. Nonlinear electromechanical modelling and dynamical behavior analysis of a satellite reaction wheel. Acta Astronaut. 2017, 141, 143–157. [Google Scholar] [CrossRef]
- Narayan, S.; Nair, P.; Ghosal, A. Dynamic interaction of rotating momentum wheels with spacecraft element. J. Sound Vib. 2008, 315, 970–984. [Google Scholar] [CrossRef]
- Wei, Z.; Li, D.; Luo, Q.; Jiang, J. Modeling and analysis of a flywheel microvibration isolation system for spacecrafts. Adv. Space Res. 2015, 55, 761–777. [Google Scholar] [CrossRef]
- Preda, V.; Cieslak, J.; Henry, D.; Bennani, S.; Falcoz, A. A H1/μ solution for microvibration mitigation in satellites: A case study. J. Sound Vib. 2017, 399, 21–44. [Google Scholar] [CrossRef]
- Preda, V.; Cieslak, J.; Henry, D.; Bennani, S.; Falcoz, A. Robust microvibration mitigation and pointing performance analysis for high stability spacecraft. Int. J. Robust Nonlinear Control 2018, 28, 5688–5716. [Google Scholar] [CrossRef]
- Zhou, W.; Li, D.; Lu, Q.; Liu, K. Analysis and testing of microvibrations produced by momentum wheel assemblies. Chin. J. Aeronaut. 2012, 25, 640–649. [Google Scholar] [CrossRef]
- Han, Q.; Li, X.; Chu, F. Skidding behavior of cylindrical roller bearings under time-variable load conditions. Int. J. Mech. Sci. 2018, 135, 203–214. [Google Scholar] [CrossRef]
- Wang, H.; Han, Q.; Zhou, D. Nonlinear dynamic modeling of rotor system supported by angular contact ball bearings. Mech. Syst. Signal Process. 2017, 85, 16–40. [Google Scholar] [CrossRef]
- Wang, H.; Han, Q.; Luo, R.; Qing, T. Dynamic modeling of moment wheel assemblies with nonlinear rolling bearing supports. J. Sound Vib. 2017, 406, 124–145. [Google Scholar] [CrossRef]
- Tang, L.; Xu, S. Geometric analysis of singularity for single-gimbal control moment gyro systems. Chin. J. Aeronaut. 2005, 18, 295–303. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, L.; Liu, Z. An improved installation for control moment gyros and its applications on reconfiguration and singular escape. Acta Astronaut. 2012, 85, 93–99. [Google Scholar]
- Huang, X.; Jia, Y.; Xu, S.; Huang, T. A new steering approach for VSCMGs with high precision. Chin. J. Aeronaut. 2016, 29, 1673–1684. [Google Scholar] [CrossRef]
- Wu, Z.; Zhang, J. Dynamics and control of gimbal servo systems for control moment gyroscopes. J. Basic Sci. Eng. 2007, 15, 130–136. [Google Scholar]
- Huang, Z.; Li, X.; Jin, D. Output characteristic analysis of single gimbal control moment gyroscope. Chin. J. Theor. Appl. Mech. 2021, 53, 511–523. [Google Scholar]
- Cui, P.; Zhang, D.; Yang, S.; Li, H. Friction compensation based on time-delay control and internal model control for a gimbal system in magnetically suspended CMG. IEEE Trans. Ind. Electron. 2017, 64, 3798–3807. [Google Scholar] [CrossRef]
- Luo, Q.; Li, D.; Zhou, W.; Jiang, J.; Yang, G.; Wei, X. Dynamic modelling and observation of micro-vibrations generated by a single gimbal control moment gyro. J. Sound Vib. 2013, 332, 4496–4516. [Google Scholar] [CrossRef]
- Luo, Q.; Li, D.; Jiang, J. Coupled dynamic analysis of a single gimbal control moment gyro cluster integrated with an isolation system. J. Sound Vib. 2014, 333, 345–363. [Google Scholar] [CrossRef]
- Shi, S.; Li, D.; Luo, Q. Design and dynamic analysis of micro-vibration isolator for Single Gimbal Control Moment Gyro. Procedia Eng. 2015, 99, 551–559. [Google Scholar] [CrossRef]
- Li, X.; Cheng, W.; Li, X. Modelling of gimbal control moment gyro and analysis of gimbal disturbance impact. Teh. Vjesn. 2014, 21, 1189–1199. [Google Scholar]
- Li, X.; Cheng, W. Research on microvibrations generated by a control moment gyroscope on a flexible interface based on a dynamic substructure method. Int. J. Aerosp. Eng. 2018, 2018, 5045740. [Google Scholar] [CrossRef]
- Wu, D.; Xie, T.; Lu, M.; Li, G.; Lai, L.; Yang, Y.; Wang, H. Modeling and experimental study on the micro-vibration transmission of a control moment gyro. IEEE Access 2019, 7, 80633–80643. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J. Disturbance characteristics analysis of CMG due to imbalances and installation errors. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1017–1026. [Google Scholar] [CrossRef]
- Zhang, J.; Guo, Z.; Zhang, Y.; Tang, L.; Guan, X. Inner structural vibration isolation method for a single control moment gyroscope. J. Sound Vib. 2016, 361, 78–98. [Google Scholar] [CrossRef]
- Wang, H.; Han, Q.; Zhou, D. Output torque modeling of control moment gyros considering rolling element bearing induced disturbances. Mech. Syst. Signal Process. 2019, 115, 188–212. [Google Scholar] [CrossRef]
- Liu, K.C.; Maghami, P.; Blaurock, C. Reaction wheel disturbance modeling, jitter analysis, and validation tests for solar dynamics observatory. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 19 August 2008; pp. 1–18. [Google Scholar]
- Park, G.; Lee, D.; Han, J. Development of multi-degree-of-freedom microvibration emulator for efficient jitter test of spacecraft. J. Intell. Mater. Syst. Struct. 2014, 25, 1069–1081. [Google Scholar] [CrossRef]
- Kim, D. Micro-vibration model and parameter estimation method of a reaction wheel assembly. J. Sound Vib. 2014, 333, 4214–4231. [Google Scholar] [CrossRef]
- Sanfedino, F.; Alazard, D.; Pommier-Budinger, V.; Boquet, F.; Falcoz, A. A novel dynamic model of a reaction wheel assembly for high accuracy pointing space missions. In Proceedings of the ASME Dynamic Systems and Control Conference (DSCC-2018), Atlanta, GA, USA, 30 September–3 October 2018. [Google Scholar]
- Lellis, S.; Stabile, A.; Aglietti, G.; Richardson, G. A semiempirical methodology to characterise a family of microvibration sources. J. Sound Vib. 2019, 448, 1–18. [Google Scholar] [CrossRef]
- Hur, G.; Kim, K. Parametric vibration source characterization of a reaction-wheel-assembly by evaluation on predictions of blocked forces and simple receiver responses. J. Mech. Sci. Technol. 2018, 32, 4433–4445. [Google Scholar] [CrossRef]
- Hur, G. Isolation of micro-vibrations due to reaction wheel assembly using a source-path-receiver approach for quantitative requirements. J. Vib. Control 2019, 25, 1424–1435. [Google Scholar] [CrossRef]
- Hasha, M. High-performance reaction wheel optimization for fine-pointing space platforms: Minimizing induced vibration effects on jitter performance plus lessons learned from hubble space telescope for current and future spacecraft applications. In Proceedings of the 43rd Aerospace Mechanisms Symposium, NASA Ames Research Center, Santa Clara, CA, USA, 4–6 May 2016. [Google Scholar]
- Inamori, T.; Wang, J.; Saisutjarit, P.; Nakasuka, S. Jitter reduction of a reaction wheel by management of angular momentum using magnetic torquers in nano- and micro-satellites. Adv. Space Res. 2013, 52, 222–231. [Google Scholar] [CrossRef]
- Kim, D.; Yoon, H.; Kang, W.; Kim, Y.; Choi, H. Development of a spherical reaction wheel actuator using electromagnetic induction. Aerosp. Sci. Technol. 2014, 39, 86–94. [Google Scholar] [CrossRef]
- Nagabhushan, V.; Fitz-Coy, N. On-orbit jitter control in momentum actuators using a three-flywheel system. Acta Astronaut. 2014, 95, 61–81. [Google Scholar] [CrossRef]
- Rodrigues, D.; Champneys, A.; Friswell, M.; Wilson, R. Automatic two-plane balancing for rigid rotors. Int. J. Non-Linear Mech. 2008, 43, 527–541. [Google Scholar] [CrossRef]
- Liu, J.; Ishida, Y. Vibration suppression of rotating machinery utilizing an automatic ball balancer and discontinuous spring characteristics. ASME J. Vib. Acoust. 2009, 131, 041004. [Google Scholar] [CrossRef]
- Horvath, R.; Flowers, G.; Fausz, J. Passive balancing of rotor systems using pendulum balancers. ASME J. Vib. Acoust. 2008, 130, 041011. [Google Scholar] [CrossRef]
- Mayr, J.; Spanlang, F.; Gattringer, H. Mechatronic design of a self-balancing three-dimensional inertia wheel pendulum. Mechatronics 2015, 30, 1–10. [Google Scholar] [CrossRef]
- Chen, H.; Ji, W.; Zhang, Q. A method for vibration isolation of a vertical axis automatic washing machine with a hydraulic balancer. J. Mech. Sci. Technol. 2012, 26, 335–343. [Google Scholar] [CrossRef]
- Cho, J.; Jeong, H.; Kong, K. Analysis of dynamic model of a top loading laundry machine with a hydraulic balancer. Int. J. Precis. Eng. Manuf. 2014, 15, 1615–1623. [Google Scholar] [CrossRef]
- Zeng, S.; Wang, X. The influence of the electromagnetic balancing regulator on the rotor system. J. Sound Vib. 1999, 219, 723–729. [Google Scholar] [CrossRef]
- Ma, S.; Pei, S.; Wang, L.; Xu, H. A novel active online electromagnetic balancing method: Principle and structure analysis. ASME J. Vib. Acoust. 2012, 134, 034503. [Google Scholar] [CrossRef]
- Hredzak, B.; Guo, G. New electromechanical balancing device for active imbalance compensation. J. Sound Vib. 2006, 294, 737–751. [Google Scholar] [CrossRef]
- Pan, X.; Wu, H.; Gao, J.; Wang, W. New liquid transfer active balancing system using compressed air for grinding machine. ASME J. Vib. Acoust. 2015, 137, 011002. [Google Scholar]
- Zhang, X.; Liu, X.; Zhao, H. New active online balancing method for grinding wheel using liquid injection and free dripping. ASME J. Vib. Acoust. 2018, 140, 031001. [Google Scholar] [CrossRef]
- Kawak, B. Development of a low-cost, low micro-vibration CMG for small agile satellite applications. Acta Astronaut. 2017, 131, 113–122. [Google Scholar] [CrossRef]
- Huang, X.; Su, Z.; Wang, S.; Wei, X.; Wang, Y.; Hua, H. High-frequency disturbance force suppression mechanism of a flywheel equipped with a flexible dynamic vibration absorber. J. Sound Vib. 2020, 26, 2113–2124. [Google Scholar] [CrossRef]
- Jacobs, J.; Meffe, M.; Hightower, R. Piezodynamic Vibration Damping System. WIPO Patent WO/2005/002967, 13 January 2005. [Google Scholar]
- Meffe, M.; Hightower, R.; Jacobs, J. Piezodynamic Preload Adjustment System. WIPO Patent WO/2005/003579A1, 30 December 2005. [Google Scholar]
- Hindle, T.; Davis, T.; Hamilton, B.; Winkel, R. Vibration Reduction System Employing Active Bearing Mounts. U.S. Patent 8002251, 23 August 2003. [Google Scholar]
- Xie, Y.; Sawada, H.; Hashimoto, T. Adaptive model following control method for actively controlled magnetic bearing momentum wheel. In Proceedings of the 5th International Symposium on Magnetic Suspension Technology, Santa Barbara, CA, USA, 11–13 December 1999; pp. 547–561. [Google Scholar]
- Xie, J.; Liu, G.; Wen, T. Composite compensation for load torque of active magnetic bearing in DGMSCMG. Opt. Precis. Eng. 2015, 23, 2211–2219. [Google Scholar]
- Cui, P.; Gai, Y.; Fang, J. Adaptive control for unbalance vibration of active-passive hybrid magnetically suspended rotor. Opt. Precis. Eng. 2015, 23, 122–131. [Google Scholar]
- Kaufmann, M.; Tuysuz, A.; Kolar, J.; Zwyssig, C. High-speed magnetically levitated reaction wheels for small satellites. In Proceedings of the 23rd International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM 2016), Anacapri, Italy, 22–24 June 2016. [Google Scholar]
- Liu, G.; Zhang, C. Sliding mode control of reaction flywheel-based brushless DC motor with buck converter. Chin. J. Aeronaut. 2013, 26, 967–975. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, K.; Ren, Y. Novel repeatable launch locking/unlocking device for magnetically suspended momentum flywheel. Mechatronics 2018, 54, 16–25. [Google Scholar]
- Tang, J.; Fang, J.; Wen, T. Superconducting magnetic bearings and active magnetic bearings in attitude control and energy storage flywheel for spacecraft. IEEE Trans. Appl. Supercond. 2012, 22, 5702109. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, M.; Han, B.; Zhang, J.; Sun, J.; Fan, Y. Research and development status of magnetic bearing technology on magnetically suspended gimballing flywheel. J. Astronaut. 2019, 40, 1251–1261. [Google Scholar]
- Bichler, U. A low noise magnetic bearing wheel for space application. In Proceedings of the 2nd International Symposium on Magnetic Bearing, Tokyo, Japan, 12–14 July 1990; pp. 1–8. [Google Scholar]
- Liu, B.; Fang, J.; Liu, G.; Fan, Y. Unbalance vibration control and experiment research of magnetically suspended flywheels. J. Mech. Eng. 2010, 46, 188–194. [Google Scholar] [CrossRef]
- Tang, J.; Liu, B.; Fang, J.; Ge, S. Suppression of vibration caused by residual unbalance of rotor for magnetically suspended flywheel. J. Vib. Control 2012, 19, 1962–1979. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S.; Zhang, Y. Automatic balancing of AMB systems using plural notch filter and adaptive synchronous compensation. J. Sound Vib. 2016, 374, 29–42. [Google Scholar] [CrossRef]
- Peng, C.; Fan, Y.; Huang, Z.; Han, B.; Fang, J. Frequency-varying synchronous micro-vibration suppression for a MSFW with application of small-gain theorem. Mech. Syst. Signal Process. 2017, 82, 432–447. [Google Scholar] [CrossRef]
- Peng, C.; Zhou, X.; Wei, T.; Ren, Y. High precision synchronous vibration suppression for a MSFW subject to phase lag influence. Mech. Syst. Signal Process. 2019, 120, 408–421. [Google Scholar] [CrossRef]
- Basaran, S.; Sivrioglu, S.; Zergeroglu, E. Composite adaptive control of single gimbal control moment gyroscope supported by active magnetic bearings. ASCE J. Aerosp. Eng. 2016, 30, 04016074. [Google Scholar] [CrossRef]
- Tang, J.; Zhao, S.; Wang, Y.; Wang, K. High-speed rotor’s mechanical design and stable suspension based on inertia-ratio for gyroscopic effect suppression. Int. J. Control Autom. Syst. 2018, 16, 1577–1591. [Google Scholar] [CrossRef]
- Deng, R.; Zhao, Y.; Fang, J.; Zhang, D. Disturbance characteristics analysis of magnetically suspended and mechanical flywheels. J. Astronaut. 2016, 37, 917–923. [Google Scholar]
- Liu, C.; Jing, X.; Daley, S.; Li, F. Recent advances in micro-vibration isolation. Mech. Syst. Signal Process. 2015, 56–57, 55–80. [Google Scholar] [CrossRef]
- Kamesh, D.; Pandiyan, R.; Ghosal, A. Passive vibration isolation of reaction wheel disturbances using a low frequency flexible space platform. J. Sound Vib. 2012, 331, 1310–1330. [Google Scholar] [CrossRef]
- Kamesh, D.; Pandiyan, R.; Ghosal, A. Modeling, design and analysis of low frequency platform for attenuating micro-vibration in spacecraft. J. Sound Vib. 2010, 329, 3431–3450. [Google Scholar] [CrossRef]
- Zhou, W.Y.; Li, D.X. Design and analysis of an intelligent vibration isolation platform for reaction/momentum wheel assemblies. J. Sound Vib. 2012, 331, 2984–3005. [Google Scholar] [CrossRef]
- Zhou, W.; Li, D. Experimental research on a vibration isolation platform for momentum wheel assembly. J. Sound Vib. 2013, 332, 1157–1171. [Google Scholar] [CrossRef]
- Wei, Z.; Li, D.; Luo, Q.; Jiang, J. Performance analysis of a flywheel microvibration isolation platform for spacecraft. J. Spacecr. Rocket. 2015, 52, 1263–1268. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, Y.; Zhang, X.; Gao, X.; Jia, K.; Xu, M. Modeling and analysis of piezoelectric folded-beam isolator for attenuating micro-vibration in spacecraft. Int. J. Comput. Mater. Sci. Eng. 2018, 7, 1850013. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, X.; Xie, S.; Yan, B.; Luo, Y. Simulated and experimental studies on a high-static-low-dynamic stiffness isolator using magnetic negative stiffness spring. Mech. Syst. Signal Process. 2017, 86, 188–203. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, G.; Zheng, G. Micro-vibration attenuation methods and key technologies for optical remote sensing satellite. J. Astronaut. 2015, 36, 125–132. [Google Scholar]
- Jiao, X.; Zhao, Y.; Ma, W. Nonlinear dynamic characteristics of a micro-vibration fluid viscous damper. Nonlinear Dyn. 2018, 92, 1167–1184. [Google Scholar] [CrossRef]
- Rodden, J.; Dougherty, H.; Reschke, L. Line-of-sight performance improvement with reaction-wheel isolation. In Proceeding of the Annual Rocky Mountain Guidance and Control Conference, Keytone, CO, USA, 1–5 February 1986; pp. 71–84. [Google Scholar]
- Wang, X.; Zheng, G. Two-step transfer function calculation method and asymmetrical piecewise-linear vibration isolator under gravity. J. Vib. Control 2016, 22, 2973–2991. [Google Scholar] [CrossRef]
- Kwon, S.; Jo, M.; Oh, H. Experimental validation of fly-wheel passive launch and on-orbit vibration isolation system by using a superelastic SMA mesh washer isolator. Int. J. Aerosp. Eng. 2017, 2017, 5496053. [Google Scholar] [CrossRef]
- Li, L.; Tan, L.; Kong, L.; Wang, D.; Yang, H. The influence of flywheel micro vibration on space camera and vibration suppression. Mech. Syst. Signal Process. 2018, 100, 360–370. [Google Scholar] [CrossRef]
- Chen, S.; Xuan, M.; Xin, J.; Liu, Y.; Gu, S.; Li, J.; Zhang, L. Design and experiment of dual micro-vibration isolation system for optical satellite flywheel. Int. J. Mech. Sci. 2020, 179, 105592. [Google Scholar] [CrossRef]
- Oh, H.; Taniwaki, S.; Kinjyo, N.; Izawa, K. Flywheel vibration isolation test using a variable-damping isolator. Smart Mater. Struct. 2006, 15, 365–370. [Google Scholar] [CrossRef]
- Magliacano, D.; Viscardi, M.; Dimino, I. Active vibration control by piezoceramic actuators of a car floor panel. In Proceedings of the 23rd International Congress on Sound and Vibration (ICSV23), Athens, Greece, 10–14 July 2016. [Google Scholar]
- Makihara, K.; Onoda, J.; Minesugi, K. New approach to semi-active vibration isolation to improve the pointing performance of observation satellites. Smart Mater. Struct. 2006, 15, 342–350. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Z.; Jiao, Y. A hybrid vibration isolator: Design, control, and experiments. Proc. IMechE C J. Mech. Eng. Sci. 2016, 230, 2982–2995. [Google Scholar] [CrossRef]
- Wang, C.; Chen, Y.; Zhang, Z. Simulation and experiment on the performance of a passive/active micro-vibration isolator. J. Vib. Control 2018, 24, 453–465. [Google Scholar] [CrossRef]
- Guan, X.; Cui, Y.; Liang, L.; Zheng, G. Development and experimental verification of flywheel vibration isolation device. In Proceeding of the Structural Vibration and Control Technology for High Resolution Remote Sensing Satellites, Changsha, China, 10–14 July 2011; pp. 38–44. [Google Scholar]
- Zhao, W.; Li, B.; Liu, P. Semi-active control for a multi-dimensional vibration isolator with parallel mechanism. J. Vib. Control 2012, 19, 879–888. [Google Scholar] [CrossRef]
- Lee, D.; Park, G.; Han, J. Experimental study on on-orbit and launch environment vibration isolation performance of a vibration isolator using bellows and viscous fluid. Aerosp. Sci. Technol. 2015, 45, 1–9. [Google Scholar] [CrossRef]
- Li, Y.; Yun, Y.; Xiao, S. Controller design and experimental investigation of a 3-universal-prismatic-universal compliant manipulator for active vibration isolation. J. Vib. Control 2015, 21, 3218–3238. [Google Scholar] [CrossRef]
- Kim, H.; Cho, Y.; Moon, J. Active vibration control using a novel three-DOF precision micro-stage. Smart Mater. Struct. 2010, 19, 055001. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, F.; Chen, X. Vibration suppression on a platform by using vibration isolation and mitigation devices. Nonlinear Dyn. 2016, 83, 1341–1353. [Google Scholar] [CrossRef]
- Xu, C.; Xu, Z.; Huang, Y.; Xu, Y.; Ge, T. Modeling and analysis of a viscoelastic micro-vibration isolation and mitigation platform for spacecraft. J. Vib. Control 2018, 24, 4337–4352. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, F.; Chen, X. Intelligent vibration isolation and mitigation of a platform by using MR and VE devices. J. Aerosp. Eng. 2016, 29, 04016010. [Google Scholar] [CrossRef]
- Spanos, J.; Rahman, Z.; Blackwood, G. A soft-axis active vibration isolator. In Proceedings of the American Control Conference, Seattle, WA, USA, 21–23 June 1995; pp. 412–416. [Google Scholar]
- Dasgupta, B.; Mruthyunjaya, T. The Stewart platform manipulator: A review. Mech. Mach. Theory 2000, 35, 15–40. [Google Scholar] [CrossRef]
- Preumont, A.; Horodinca, M.; Romanescu, I.; Marneffe, B.; Avraam, M.; Deraemaeker, A.; Bossens, F.; Hanieh, A. A six-axis single-stage active vibration isolator based on Stewart platform. J. Sound Vib. 2007, 300, 644–661. [Google Scholar] [CrossRef]
- Pendergast, K.; Schauwecker, C. Use of a passive reaction wheel jitter isolation system to meet the advanced X-ray astrophysics facility imaging performance requirements. In Proceedings of the SPIE Conference on Space Telescopes and Instruments V, Kona, HI, USA, 20 March 1998; Volume 3356, pp. 1078–1094. [Google Scholar]
- Lee, D.; Park, G.; Han, J.H. Hybrid isolation of micro vibrations induced by reaction wheels. J. Sound Vib. 2016, 363, 1–17. [Google Scholar] [CrossRef]
- Yang, X.; Wu, H.; Li, Y.; Chen, B. Dynamic isotropic design and decentralized active control of a six-axis vibration isolator via Stewart platform. Mech. Mach. Theory 2017, 117, 244–252. [Google Scholar] [CrossRef]
- Yang, X.; Wu, H.; Chen, B.; Kang, S.; Cheng, S. Dynamic modeling and decoupled control of a flexible Stewart platform for vibration isolation. J. Sound Vib. 2019, 439, 398–412. [Google Scholar] [CrossRef]
- Qin, C.; Xu, Z.; Xia, M.; He, S.; Zhang, J. Design and optimization of the micro-vibration isolation system for large space telescope. J. Sound Vib. 2020, 482, 115461. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, K.; Jiao, J.; Zhao, R. Dynamic modeling and robust nonlinear control of a six-DOF active micro-vibration isolation manipulator with parameter uncertainties. Mech. Mach. Theory 2015, 92, 407–435. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, K.; Jiao, J.; Cao, D.; Chi, W.; Tang, J. Dynamic isotropy design and analysis of a six-DOF active micro-vibration isolation manipulator on satellites. Robot. Comput.-Integr. Manuf. 2018, 49, 408–425. [Google Scholar] [CrossRef]
- Hauge, G.; Campbell, M. Sensors and control of a space-based six-axis vibration isolation system. J. Sound Vib. 2004, 269, 913–931. [Google Scholar] [CrossRef]
- Anderson, E.; Fumo, J.; Erwin, R. Satellite ultra-quiet isolation technology experiment (SUITE). In Proceedings of the IEEE Aerospace Conference, Piscataway, NJ, USA, 25 March 2000; pp. 299–313. [Google Scholar]
- Wang, C.; Xie, X.; Chen, Y.; Zhang, Z. Investigation on active vibration isolation of a Stewart platform with piezoelectric actuators. J. Sound Vib. 2016, 383, 1–19. [Google Scholar] [CrossRef]
- Yun, H.; Liu, L.; Li, Q.; Yang, H. Investigation on two-stage vibration suppression and precision pointing for space optical payloads. Aerosp. Sci. Technol. 2020, 96, 105543. [Google Scholar] [CrossRef]
- Sun, X.; Yang, B.; Zhao, L.; Sun, X. Optimal design and experimental analyses of a new micro-vibration control payload-platform. J. Sound Vib. 2016, 374, 43–60. [Google Scholar] [CrossRef]
- Thayer, D.; Campbell, M.; Vagners, J. Six-axis vibration isolation system using soft actuators and multiple sensors. J. Spacecr. Rocket. 2002, 39, 206–212. [Google Scholar] [CrossRef]
- Beijen, M.; Heertjes, M.; Dijk, J.; Hakvoort, W. Self-tuning MIMO disturbance feedforward control for active hard-mounted vibration isolators. Control Eng. Pract. 2018, 72, 90–103. [Google Scholar] [CrossRef]
- Zhang, Y.; Sheng, C.; Hu, Q.; Li, M.; Guo, Z.; Qi, R. Dynamic analysis and control application of vibration isolation system with magnetic suspension on satellites. Aerosp. Sci. Technol. 2018, 75, 99–114. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, Y.; Hu, Q. Integrated vibration isolation and attitude control for spacecraft with uncertain or unknown payload inertia parameters. Acta Astronaut. 2018, 151, 107–119. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S. Vibration isolation platform for control moment gyroscopes on satellites. J. Aerosp. Eng. 2012, 25, 641–652. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, Z.; He, H.; Zhang, J.; Liu, M.; Zhou, Z. A novel vibration isolation system for reaction wheel on space telescopes. Acta Astronaut. 2014, 102, 1–13. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, J. The imaging stability enhancement of optical payload using multiple vibration isolation platforms. J. Vib. Control 2015, 21, 1848–1865. [Google Scholar]
- Zhang, Y.; Zang, Y.; Li, M.; Wang, Y.; Li, W. Active-passive integrated vibration control for control moment gyros and its application to satellites. J. Sound Vib. 2017, 394, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.; Sheng, C.; Guo, Z.; Wang, Y.; Li, W. Dynamic characteristics and performance evaluation for the part strut failure of the vibration isolation platform on satellites. Acta Astronaut. 2017, 133, 403–415. [Google Scholar] [CrossRef]
- Heiberg, C.; Bailey, D.; Wie, B. Precision spacecraft pointing using single-gimbal control moment gyroscopes with disturbance. J. Guid. Control Dyn. 2000, 23, 77–85. [Google Scholar] [CrossRef]
- Huang, X.; Sun, J.; Hua, H.; Zhang, Z. Modeling and optimization of octostrut vibration isolation platform by FRF-based substructuring method. J. Aerosp. Eng. 2015, 28, 04014084. [Google Scholar] [CrossRef]
- Luo, Q.; Li, D.; Jiang, J. Analysis and optimization of micro-vibration isolation for multiple flywheel systems of spacecraft. AIAA J. 2016, 54, 1719–1731. [Google Scholar] [CrossRef]
- Wu, Q.; Yue, H.; Liu, R.; Zhang, X.; Ding, L.; Liang, T.; Deng, Z. Measurement model and precision analysis of accelerometers for maglev vibration isolation platforms. Sensors 2015, 15, 20053–20068. [Google Scholar] [CrossRef] [PubMed]
- Gong, Z.; Ding, L.; Yue, H.; Gao, H.; Liu, R.; Deng, Z.; Lu, Y. System integration and control design of a maglev platform for space vibration isolation. J. Vib. Control 2019, 25, 1720–1736. [Google Scholar] [CrossRef]
- Gong, Z.; Ding, L.; Li, S.; Yue, H.; Gao, H.; Deng, Z. Payload-agnostic decoupling and hybrid vibration isolation control for a maglev platform with redundant actuation. Mech. Syst. Signal Process. 2021, 146, 106985. [Google Scholar] [CrossRef]
- Xiao, X.; Jing, X.; Cheng, L. The transmissibility of vibration isolators with cubic nonlinear damping under both force and base excitations. J. Sound Vib. 2013, 332, 1335–1354. [Google Scholar] [CrossRef]
- Sun, J.; Huang, X.; Liu, X.; Xiao, F.; Huang, H. Study on the force transmissibility of vibration isolators with geometric nonlinear damping. Nonlinear Dyn. 2013, 74, 1103–1112. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.; Zheng, W.; Jian, B.; Wang, K.; Wu, C. Nonlinear electromagnetic shunt damping for nonlinear vibration isolators. IEEE/ASME Trans. Mechatron. 2019, 24, 1851–1860. [Google Scholar] [CrossRef]
- Yan, B.; Ma, H.; Zhang, L.; Zheng, W.; Wang, K.; Wu, C. A bistable vibration isolator with nonlinear electromagnetic shunt damping. Mech. Syst. Signal Process. 2020, 136, 106504. [Google Scholar] [CrossRef]
- Ma, H.; Yan, B. Nonlinear damping and mass effects of electromagnetic shunt damping for enhanced nonlinear vibration isolation. Mech. Syst. Signal Process. 2021, 146, 107010. [Google Scholar] [CrossRef]
- Stabile, A.; Aglietti, G.; Richardson, G.; Smet, G. Design and verification of a negative resistance electromagnetic shunt damper for spacecraft micro-vibration. J. Sound Vib. 2017, 386, 38–49. [Google Scholar] [CrossRef]
- Stabile, A.; Aglietti, G.; Richardson, G.; Smet, G. A 2-collinear-DoF strut with embedded negative-resistance electromagnetic shunt dampers for spacecraft micro-vibration. Smart Mater. Struct. 2017, 26, 045031. [Google Scholar] [CrossRef]
- Zhou, J.; Xiao, Q.; Xu, D.; Ouyang, H.; Li, Y. A novel quasi-zero-stiffness strut and its applications in six-degree-of-freedom vibration isolation platform. J. Sound Vib. 2017, 394, 59–74. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Q.; Yan, B.; Luo, Y.; Zhang, X. A Stewart isolator with high-static-low-dynamic stiffness struts based on negative stiffness magnetic springs. J. Sound Vib. 2018, 422, 390–408. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, X.; Luo, Y.; Zhang, Y.; Xie, S. Analytical study of the low frequency multi-direction isolator with high-static-low-dynamic stiffness struts and spatial pendulum. Mech. Syst. Signal Process. 2018, 110, 521–539. [Google Scholar] [CrossRef]
- Palomares, E.; Nieto, A.; Moreales, A.; Chicharro, J.; Pintado, P. Numerical and experimental analysis of a vibration isolator equipped with a negative stiffness system. J. Sound Vib. 2018, 414, 31–42. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X.; Li, F. Vibration isolation using a hybrid lever-type isolation system with an X-shape supporting structure. Int. J. Mech. Sci. 2015, 98, 169–177. [Google Scholar] [CrossRef]
- Wang, Y.; Jing, X.; Guo, Y. Nonlinear analysis of a bio-inspired vertically asymmetric isolation system under different structural constraints. Nonlinear Dyn. 2019, 95, 445–464. [Google Scholar] [CrossRef]
- Wang, Y.; Jing, X. Nonlinear stiffness and dynamical response characteristics of an asymmetric X-shaped structure. Mech. Syst. Signal Process. 2019, 125, 142–169. [Google Scholar] [CrossRef]
- Sun, M.; Song, G.; Li, Y.; Huang, Z. Effect of negative stiffness mechanism in a vibration isolator with asymmetric and high-static-low-dynamic stiffness. Mech. Syst. Signal Process. 2019, 124, 388–407. [Google Scholar] [CrossRef]
- Yang, G.; Zou, H.; Wang, S.; Zhao, L.; Gao, Q.; Tan, T.; Zhang, W. Large stroke quasi-zero stiffness vibration isolator using three-link mechanism. J. Sound Vib. 2020, 478, 115344. [Google Scholar]
- Liu, H.; Wang, Y.; Shi, W. Vibration suppression for a flywheel based on nonlinear energy sink. J. Astronaut. 2017, 38, 490–496. [Google Scholar]
- Sun, Y.; Zhang, Y.; Ding, H.; Chen, L. Nonlinear energy sink for a flywheel system vibration reduction. J. Sound Vib. 2018, 429, 305–324. [Google Scholar] [CrossRef]
- Sun, X.; Zhang, S.; Xu, J. Parameter design of a multi-delayed isolator with asymmetrical nonlinearity. Int. J. Mech. Sci. 2018, 138–139, 398–408. [Google Scholar] [CrossRef]
- Chen, S.; Xuan, M.; Zhang, L.; Gu, S.; Gong, X.; Sun, H. Simulating and testing microvibrations on an optical satellite using acceleration sensor-based jitter measurements. Sensors 2019, 19, 1797. [Google Scholar] [CrossRef]
- Chen, J.; Cheng, W. Low-frequency compensation of piezoelectric micro-vibrations test platform. Teh. Vjesn. 2016, 23, 1251–1258. [Google Scholar]
- Xia, M.; Xu, Z.; Han, K.; Huo, Q.; Li, A. Dynamic disturbance force measurement platform for large moving device in spacecraft. J. Sound Vib. 2019, 447, 61–77. [Google Scholar] [CrossRef]
- Elias, L. A Structurally Coupled Disturbance Analysis Method Using Dynamic Mass Measurement Techniques, with Application to Spacecraft-Reaction Wheel Systems; Massachusetts Institute of Technology: Cambridge, MA, USA, 2001. [Google Scholar]
- Zhao, Y.; Zhang, P.; Cheng, W. Measurement and study of disturbance characteristics of reaction wheel assembly. J. Exp. Mech. 2009, 24, 532–538. [Google Scholar]
- Taniwaki, S.; Kudo, M.; Sato, M. Analysis of retainer induced disturbances of reaction wheel. J. Syst. Des. Dyn. 2007, 1, 307–317. [Google Scholar] [CrossRef]
- Taniwaki, S.; Hatsutori, Y.; Ohkami, Y. Development of lower frequency disturbance detector for reaction wheel analysis. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005. IMECE2005-79318. [Google Scholar]
- Wang, X.; Xu, Z.; He, S.; Wu, Q.; Li, H.; Zhao, Y.; He, L. Modeling and analysis of a multi-degree-of-freedom micro-vibration simulator. Shock Vib. 2017, 2017, 4840514. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Z.; Xia, M.; He, S.; Li, H.; Wu, Q. Research on a six-degree-of-freedom disturbance force and moment simulator for space micro-vibration experiments. J. Sound Vib. 2018, 432, 530–548. [Google Scholar] [CrossRef]


| Model Types | Current Studies | SFRS Types | DoFs | Disturbances | Applications | |||
|---|---|---|---|---|---|---|---|---|
| Ⓐ | Ⓑ | Ⓒ | Ⓓ | |||||
| Empirical | [53,54,55,56,57,58] | RWA | —— | √ | √ | x | x | Micro-vibration analysis of the whole spacecraft |
| [59,60,61,62] | RWA | —— | √ | √ | x | √ | Influence of assembly error on micro vibration | |
| [63,64] | CMG | —— | √ | √ | x | x | Multiple disturbances with higher accuracy in lower bandwidth | |
| Analytical | [19,65,66,67] | RWA | 4 | √ | x | x | x | Natural characteristics and whirl response |
| [68,69,70,71,72,73,74,75,76] | MWA | 5 † | √ | x | x | √ | Dynamic coupling between the installation foundation and SFRS | |
| [77,78,79,80] | RWA | 5 ‡ | √ | x | √ | √ | Torsional and radial vibrations of SFRS | |
| [81,82,83,84] | RWA | 6 | √ | x | x | √ | Dynamic coupling between SFRS and its bracket | |
| [85,86,87,88] | MWA | 5 † | √ | √ | x | √ | Nonlinear stiffness of rolling bearing and surface waviness excitation | |
| [95,96,97,98,99,100,101,102,103] | CMG | 5 + 3 § | √ | √ | x | √ | Micro-vibration and dynamic output torque characteristics of CMG | |
| Hybrid | [104,105,106,107] | RWA | —— | √ | x | x | x | Interference modeling and jitter analysis of the RWA in SDO |
| [108,109,110] | RWA | —— | √ | x | x | √ | Typical behavior of a series of micro-vibration sources of RWA | |
| Suppression Techniques | Current Studies | Advantages | Disadvantages | Applications |
|---|---|---|---|---|
| Low disturbance flywheel technology | Multi-wheel structure [114] | Low precision dynamic balancing treatment; high reliability | Difficult to eliminate disturbances of rolling bearing | Prototype |
| Passive type of automatic balancing device [115,116,117,118,119,120] | Simple structure, high reliability, no requirement for external energy | Increasing imbalance in subcritical state | Not yet used in SFRSs | |
| Active type of automatic balancing device [121,122,123,124,125] | Flexible adjustment, fast balancing, balancing effect for both rigid and flexible rotors | Great changes to rotor structure, needs additional energy | Not yet used in SFRSs | |
| Elastic supports | Viscoelastic damping material [68,69,70,71,72,73,126,127] | Passive type, high reliability, no requirement for external energy | Changes to the structure, limited effect on low-frequency micro vibration | Widely used in SFRSs |
| Piezoelectric damping material [128,129,130] | Intelligent support, wide band micro-vibration suppression | Needs dissipative circuits | Prototype | |
| Maglev bearing | [132,133,134,135,136,137,138,139,140,141,142,143,144,145,146,147] | No contact, no friction, no lubrication, high precision, long service life | Complex structure, high power consumption | Demonstration application in SFRSs |
| Damping Types | Advantages | Disadvantages | Applications |
|---|---|---|---|
| Viscous damping | Various forms, high damping ratio | Greatly affected by temperature, aging gassing problem, strength problem | Distributed, independent |
| Fluid damping | Large damping force | Potential leakage risk, easy to jam under zero gravity | Independent |
| Eddy current damping | All metal, high sensitivity | Relatively small damping force under the same volume | Used inside the vibration isolator |
| Dry friction damping | All metal | Sound effect only in large deformation | Used in joint parts |
| Particle damping | Not affected by temperature | Nonlinear, low energy-loss factor, only suitable for large load conditions, needs special design of anti-weight device | Independent cavity |
| Isolation Techniques | Current Studies | Advantages | Disadvantages | Applications |
|---|---|---|---|---|
| Folded beam structure | [149,150,151,152,153,154,155] | Simple structure; easy to achieve active isolation | Affected by gyroscopic effect; not suitable for non-fixed type SFRSs | Prototype |
| Rod element | Unidirectional platform [158,159,160,161,162,163,164,165,166,167] | Axial isolation; both semi-active/active isolation can be achieved; high reliability | Single direction isolation; unsuitable for multi-directional isolation | Widely used in SFRSs |
| Three-leg platform [168,169,170,171,172,173,174,175] | Multi-directional vibration isolation; both translational/rotational directions can be achieved; wider frequency range | Uncertainty exists in support stiffness; unsuitable for omni-directional isolation | Prototype | |
| Six-leg platform [176,177,178,179,180,181,182,183,184,185,186,187,188,189,190,191,192,193,194,195,196,197,198,199] | Omni-directional vibration isolation; both passive/active isolation can be achieved; good versatility | Motion coupling between rod elements; complicated structure | Used in actual SFRSs | |
| Eight-leg platform [200,201,202] | Omni-directional vibration isolation; suitable for groups of SFRSs; high reliability | Complicated structure; difficult to control | Used in actual SFRSs | |
| Maglev technology | [203,204,205] | Non-contact; non-friction; long travel; suitable for low-frequency vibration isolation | Complicated structure; high power consumption | Prototype |
| Introduction of nonlinear factors | Nonlinear damping [206,207,208,209,210,211,212] | Wide operational frequency band; both semi-active/active isolation can be achieved | Poor performance in lower-frequency band | Prototype |
| Nonlinear stiffness [213,214,215,216,217,218,219,220,221] | Excellent performance at low-frequency band; both passive/active isolation can be achieved; high static stiffness; low dynamic stiffness | Complicated structure; reliability needs to be improved | Prototype |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Q.; Gao, S.; Chu, F. Micro-Vibration Analysis, Suppression, and Isolation of Spacecraft Flywheel Rotor Systems: A Review. Vibration 2024, 7, 229-263. https://doi.org/10.3390/vibration7010013
Han Q, Gao S, Chu F. Micro-Vibration Analysis, Suppression, and Isolation of Spacecraft Flywheel Rotor Systems: A Review. Vibration. 2024; 7(1):229-263. https://doi.org/10.3390/vibration7010013
Chicago/Turabian StyleHan, Qinkai, Shuai Gao, and Fulei Chu. 2024. "Micro-Vibration Analysis, Suppression, and Isolation of Spacecraft Flywheel Rotor Systems: A Review" Vibration 7, no. 1: 229-263. https://doi.org/10.3390/vibration7010013
APA StyleHan, Q., Gao, S., & Chu, F. (2024). Micro-Vibration Analysis, Suppression, and Isolation of Spacecraft Flywheel Rotor Systems: A Review. Vibration, 7(1), 229-263. https://doi.org/10.3390/vibration7010013





