Abstract
We theoretically study the dynamical Casimir effect (DCE), i.e., parametric amplification of a quantum vacuum, in an optomechanical cavity interacting with a photonic crystal, which is considered to be an ideal system to study the microscopic dissipation effect on the DCE. Starting from a total Hamiltonian including the photonic band system as well as the optomechanical cavity, we have derived an effective Floquet–Liouvillian by applying the Floquet method and Brillouin–Wigner–Feshbach projection method. The microscopic dissipation effect is rigorously taken into account in terms of the energy-dependent self-energy. The obtained effective Floquet–Liouvillian exhibits the two competing instabilities, i.e., parametric and resonance instabilities, which determine the stationary mode as a result of the balance between them in the dissipative DCE. Solving the complex eigenvalue problem of the Floquet–Liouvillian, we have determined the stationary mode with vanishing values of the imaginary parts of the eigenvalues. We find a new non-local multimode DCE represented by a multimode Bogoliubov transformation of the cavity mode and the photon band. We show the practical advantage for the observation of DCE in that we can largely reduce the pump frequency when the cavity system is embedded in a narrow band photonic crystal with a bandgap.
1. Introduction
A vacuum fluctuation is one of the most characteristic features of quantum mechanics, which has no classical analog [1]. Lamb shift [2] and spontaneous emission [3,4] are well-known examples of the effects of vacuum fluctuation on an atom. The static Casimir effect is another example where an attractive force is working on electrically neutral bodies due to an exchange of virtual photons surrounding the material [5,6]. In contrast to these effects, the dynamical Casimir effect (DCE) provides a more direct method to observe the quantum vacuum fluctuation. The rapid motion of the boundary of an electromagnetic field invokes the conversion of localized virtual photons to real photons, which can be detected at large distances [7,8,9,10]. The DCE has also intrigued scientists because of its close relation to Hawking radiation and the Unruh effect [10].
Despite this interest, it has been difficult to experimentally observe the DCE because it requires a fast motion of the macroscopic body with almost the velocity of light [7,8]. Almost 40 years after the prediction by Moore, a few experiments to observe the DCE have succeeded with the use of a superconducting circuit to effectively change the boundary condition of the optical transmission line as well as the observation of the quantum nature of the emitted field, such as entangled photons and the squeezing effect [11,12].
Two exponential instabilities play a key role in the DCE. The first is a quantum parametric amplification of a vacuum fluctuation, where a periodical change of an oscillator frequency enhances a virtual transition to yield a squeezed vacuum represented by the Bogoliubov transformation [13,14]. When an external pump frequency comes close to twice the oscillator fundamental frequency, the bifurcation of the exponential amplification–deamplification instability appears [13,14,15,16,17]. The second is a resonance instability at which the irreversible transition from the amplified virtual photon to a real observable photon appears as a spontaneous photon emission to a free radiation field with exponential decay. The point where the bifurcation of the resonance instability occurs is known as the exceptional point [18,19]. The stationary energy flow to the free radiation field emerges as a result of a balance between the parametric amplification and the dissipation processes with exponential growth and decay.
Since these two instabilities are dynamical processes, they are expected to be interpreted in a unified manner within quantum dynamics. Nevertheless, while the parametric instability has been well formulated by using the Bogoliubov transformation [13,14], the resonance instability has brought about a serious problem regarding how to derive the irreversibility based on the reversible microscopic principle of dynamics [20,21,22,23]. Ordinary textbooks of quantum mechanics state that a Hermitian Hamiltonian in the Hilbert space only possesses real eigenvalues, seemingly contradicting the well known fact that a discrete state coupling with a continuum exponentially decays with a decay rate evaluated by the resonance pole of the Green’s function [24].
Conventional descriptions of the dissipation processes in the DCE are input–output theories [25,26] and quantum master equation methods [17,27,28]. Since these theories are mostly based on the Markov approximation assuming an infinite bandwidth of the free radiation field, they are insufficient to describe the DCE photon emission to a narrow-bandwidth photonic crystal with a bandgap [29,30,31,32,33]. Recent advances in hybrid quantum systems, such as optomechanical systems where a photon emission process is manipulated at a single photon level, require a theory of DCE taking into account a microscopic dissipation mechanism [34,35,36,37,38,39].
Recently, for the microscopic description of the dissipation process within a quantum mechanics, new formalisms, known as complex spectral analysis [40,41,42,43] and non-Hermitian quantum mechanics [18,19,44,45], have been independently developed. In the complex spectral analysis, the functional space for a quantum state is extended to the rigged Hilbert space where the dual functional space is equipped with a bi-complete and bi-orthonormal basis set [21,22], so that the time-evolution generator, Hamiltonian or Liouvillian, has complex eigenvalues. We have applied this theory to open quantum systems to study dissipation processes of a discrete quantum state interacting with a continuum with a finite bandwidth. We have revealed that the decay is nonanalytically enhanced when the discrete state is located closely to the band edge of the continuum, and, as a result, it shows a nonanalytic decay process [46,47,48,49]. Therefore, in order to describe the DCE of a hybrid quantum system, it is important to take into account the effect of the energy-dependent self-energy.
In the present paper, we theoretically study the parametric amplification of a quantum vacuum of an optomechanical cavity interacting with a photonic band, where the mirror boundary is periodically moved by a classical external force, as shown in Figure 1a. The total system is composed of optomechanical cavity and photonic band states, and the time evolution of the operators of the canonical variables obeys the Heisenberg equation, where the generator of the time evolution is the Liouvillian. With the use of the Floquet method, we have transformed the time-dependent problem to a time-independent eigenvalue problem in Floquet space [17,50,51]. The non-Hermitian effective Liouvillian is derived in terms of the Brillouin–Wigner–Feshbach projection operator methods, where the microscopic dissipation process is rigorously taken into account with an energy-dependent self energy [52,53,54,55,56]. The complex eigenvalue problem of the effective Floquet–Liouvillian is solved to obtain new normal modes in terms of the multimode Bogoliubov transformation, where the stationary mode is determined by the one with a vanishing imaginary part of its eigenvalue as a result of the balance between the parametric amplification and the dissipation. We have found that we can stabilize the nonlocal mode, taking advantage of this balance when the cavity mode frequency lies in a photonic bandgap and that we can reduce the pump frequency to cause the DCE. Our proposal provides an alternative method to that of Refs. [36,37] for removing a major difficulty in generating DCE photon emission.
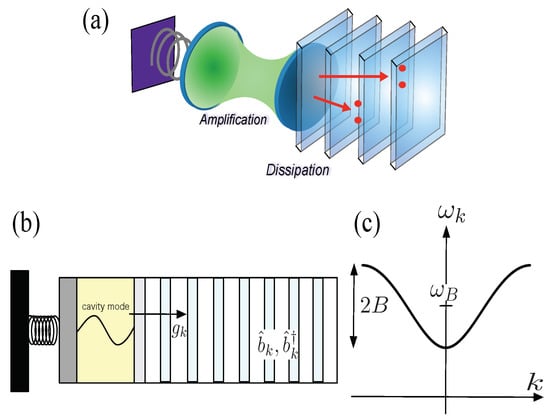
Figure 1.
(a) optomechanical cavity interacting with a photonic crystal; (b) the frequency of a single cavity mode is periodically changed by mechanical pumping, and the cavity mode photon decays into a one-dimensional photonic band; (c) dispersion relation of a one-dimensional photonic band with a bandwidth of and the central frequency .
In Section 2, we show the model of a hybrid quantum system consisting of optomechanical cavity and photonic crystal, and the total Hamiltonian for the system. With the use of the Floquet method, we transform the Heisenberg equation to the time-independent complex eigenvalue problem of Floquet–Liouvillian. The effective Floquet–Liouvillian is derived by using a Brillouin–Wigner–Feshbach projection method, where the microscopic dissipation effect is rigorously taken into account in terms of the energy-dependent self-energy, associated with the detailed derivation in Appendix A. We show the calculated results in Section 3, where the competition between the parametric amplification and the dissipation may be clear. We also compare our results with that of a simpler phenomenological model to illustrate the significant role to give rise to a nonlocal stationary mode. The emergence of the nonlocal multimode DCE will be revealed as a result of the band edge effect of the photonic band. We conclude our results in Section 4, emphasizing the possible reduction of the external field frequency for the DCE.
2. Model and Floquet–Liouvillian
We consider a hybrid quantum system consisting of optomechanical cavity and one-dimensional photonic crystal, as shown in Figure 1a, where we assume a single cavity mode in the cavity and a one-dimensional photonic band represented by a tight-binding model for the photonic crystal as shown in Figure 1b. The cavity mode decays into photonic band through the transmitting mirror on one side of the cavity. An external mechanical force oscillates a boundary mirror on the other side of the cavity with a frequency , which periodically changes the cavity mode frequency.
The total system is represented by the Hamiltonian [57,58]
where () and () are the creation (annihilation) operators of the cavity mode and photonic band, respectively, and is taken in the present paper. The effect of the external mechanical force on the cavity mode is represented by a change of the cavity mode frequency in the second term
where , , and are the pumping frequency, the amplitude, and the initial phase, respectively. The photonic band is described by a one-dimensional tight-binding model whose dispersion relation is given by
as shown in Figure 1c. The interaction of the cavity with the photonic band is described by the last term of (1), where the coupling strength for each k mode is given by with a coupling constant g. We adopt the rotating wave approximation as for the interaction between the cavity mode and the photonic band.
The Heisenberg equation of the dynamical variables is written by
The generator of time evolution is obtained from the commutation relation with the Hamiltonian that is now represented by a matrix in (4) that we shall call Liouvillian matrix . Note that the virtual transition interactions appear in the off-diagonal matrix elements hybridizing the and of the cavity modes. As a result, these modes at time t are represented by the Bogoliubov transform which changes a bare vacuum state to a squeezed vacuum state [14,59]. In (4), the column vector of the operators represents the field operator of the radiation field
where ’s are time-independent basis used in the second quantization of the radiation field [60]. We assume that this mode basis forms an orthonormal complete basis set:
The field operator can be also expanded by the solutions of scalar wave equations
where is the Liouvillian matrix in (4). Then, the field operator is expanded by the mode functions as in Ref. [15],
where defines the mode operator corresponding to .
Since is time-periodic, the wave Equation (7) can be solved by the Floquet method. We can write the solution as [17,50,51]
where , is the quasi-eigenvalue of the Floquet–Liouvillian, and the is the corresponding eigenstate satisfying
In terms of the Floquet transform, the continuous time variable t is transformed to the discrete Floquet mode variables, by means of which the time-dependent differential Equation (7) turns into time-independent complex eigenvalue problem of the Floquet–Liouvillian in the Floquet space. As shown in Appendix A, the Floquet space (-space) is composed of the coordinate space and the temporal space of periodic functions in time with period T. The orthonormal basis set in the -space is formed by a direct product of the - and the -spaces: , where is the basis state of the -space and denotes the Floquet mode basis state in the -space. In the following, we simply write for . It is found that the virtual transition interactions couple the creation and annihilation modes of the cavity belonging to a next neighbor Floquet mode, making non-Hermitian.
Under the condition of
which is satisfied for the narrow photonic band and small external amplitude, we can restrict ourselves to space. By using the projection operator methods [52], we derive the effective Floquet Liouvillian in terms of the cavity modes of given by
as shown in Appendix A. For the present one-dimensional photonic band, the self-energy is analytically obtained by
As seen from (12), the two competing instabilities mentioned in the Introduction clearly appear in the effective Liouvillian. The virtual transition in the off-diagonal elements and the complex self-energy in the diagonal elements represent the parametric instability and the resonance instability, respectively. Therefore, the effective Liouvillian describes the exponential instabilities in the DCE from a unified point of view.
Now, the complex eigenvalue problem of the total Floquet–Liouvillian is reduced to the one of the effective Liouvillian, which reads
where the complex eigenstates form a bi-orthonormal bi-complete basis set [21]:
The complex eigenvalues in (14) are obtained by solving the dispersion equation
By squaring the square root functions, this dispersion equation turns into an eighth-order polynomial equation, which has been numerically solved. Among the solutions, we found the four solutions continuously connecting to the unperturbed modes. The physical origin of the four solutions are assigned to a mixture of the resonance and antiresonance modes for each of cavity creation and annihilation modes, as shown in Figure 2.
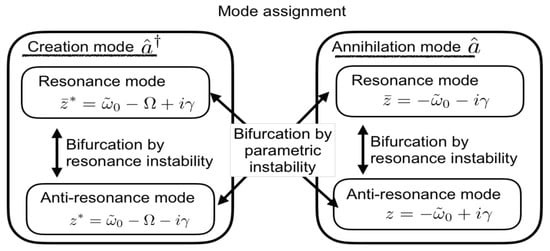
Figure 2.
Characteristic origin of the eigenmodes of the system.
In terms of the complex spectral analysis, we can define the stationary mode based on the microscopic dynamics as a mode whose eigenvalue has a vanishing value of the imaginary part, i.e., , without relying on Markov approximation. In the next section, we shall see the profound effect of the band edge of photonic band on the generation of the real photon emission in the dynamical Casimir effect of the hybrid quantum system.
3. Results
In order to show the effect of the balance between the parametric amplification and the dissipation, we show the imaginary parts of the eigenvalues of for in Figure 3, where we change the cavity frequency while the values of and are fixed. As shown in Figure 3b, the neighboring Floquet-photonic bands are overlapped.
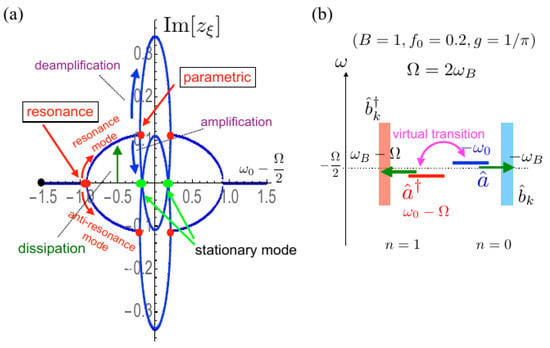
Figure 3.
(a) imaginary part of the complex eigenvalues of as a function of for the coupled optomechanical cavity with the photonic band, where the parameters are taken , , , and . The horizontal axis represents . The bifurcation points are indicated by the red filled circles, and the stationary points are indicated by the green filled circles; (b) Floquet–Liouvillian level scheme of the , and states, where the vertical axis denotes the frequencies of the modes in the Floquet–Liouvillian. The dotted line is drawn at as a guide.
As increases, we encounter the bifurcation of the resonance instability at , where the cavity mode becomes resonant with the photonic band, resulting in the bifurcation to resonance and anti-resonance modes as in the other decaying systems [46,49,61,62]. In this figure, a positive indicates a decaying state since as shown in (9). With a further increase of , the frequencies of the creation and annihilation cavity modes come close, and the effect of the virtual transition between them becomes significant. Then, we encounter the second bifurcation of parametric instability at , where the downward and upward branches correspond to the parametric amplification and deamplification, respectively. As we further increase , we reach the stationary point where , as a result of a balance between the parametric amplification and the dissipation effects, as indicated by the green filled circle. At this point, the stationary energy flow through the cavity from the external pump to the photonic band is achieved with the spontaneous photon pair emission. The figure clearly demonstrates that this stationary DCE has been determined by taking into account the microscopic dissipation process.
Here, we compare the present results with a phenomenological theory. We write a phenomenological effective Floquet–Liouvillian
consistent with an equation of motion of a forced damped oscillator
where
and is a phenomenological dissipation constant. The complex eigenvalue is immediately obtained by
In Figure 4, we show the imaginary part of the above solutions. Since this phenomenological model assumes a flat-band radiation with infinite bandwidth, the resonance bifurcation does not appear, though we see the stationary mode as a balance between the constant dissipation and parametric amplification. What seems unphysical in (20), however, is its initial phase dependence of the results as shown in Figure 4a,b. It is irrational that the stationary point depends on the initial phase of the external field. Contrary to this unphysical result, the correct result based on the microscopic model does not depend on the phase factor, as seen from (16).
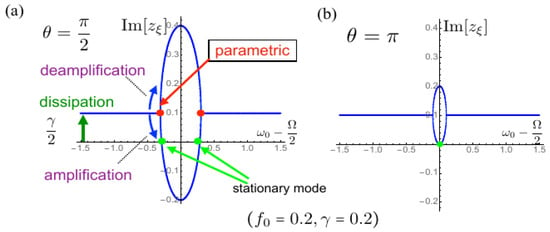
Figure 4.
Imaginary part of the complex eigenvalues of the phenomenological model as a function of for the values of and , where the horizontal axis represents . (a) , and (b) .
The band edge effect is more pronounced when lowering the external pumping frequency. In Figure 5, we show the results for with so that the neighboring Floquet photonic bands are shifted by , as shown in Figure 5c, where other parameters are fixed at the same values of Figure 3. The overall behavior of is shown in Figure 5a, where we have seen essentially the same stationary points, indicated by the green filled circles, as a result of the balance between the resonance instability and the parametric amplification of the cavity modes.
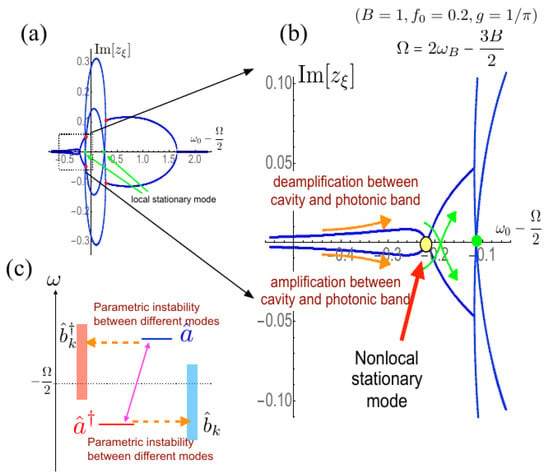
Figure 5.
(a) overall picture of the imaginary part of the complex eigenvalues of as a function of for the coupled optomechanical cavity with the photonic band, where the parameters are taken , , , , and . The horizontal axis represents . The bifurcation points are indicated by the red filled circles, and the stationary points are indicated by the green filled circle; (b) expanded picture of the dotted box area in (a). Non-local multimode stationary point is indicated by the yellow filled circle; (c) Floquet–Liouvillian level scheme of the , and states, where the vertical axis denotes the frequencies of the modes in the Floquet–Liouvillian. The dotted line is drawn at as a guide.
However, in the region where the cavity mode frequency is located around the band edge, i.e., , we can see the other type of the stationary point. We show the result in the expanded scale in Figure 5b, and the Floquet–Liouvillian level scheme in this region is shown in Figure 5c. In this region, the creation (annihilation) cavity mode is in resonance with the annihilation (creation) mode of the photonic band. Even though there is no direct coupling between them, there is an indirect coupling via the virtual transition of the cavity modes, as shown in Figure 5c. Consequently, the eigenmode of the total system is represented by the multimode-Bogoliubov transformation of the cavity mode and the continuous photonic band [59]. This mixing of the creation and annihilation modes between them induces the non-local multimode parametric instability, as shown by the orange arrows in Figure 5b.
As further increases so that the creation (annihilation) cavity mode is in resonance with the corresponding photonic band modes, the multimode parametric instability is suppressed by the dissipation effect. As a result of the balance between them, the nonlocal stationary point emerges, which is indicated by the yellow filled circle in Figure 5b. This stationary mode is characteristically different from the previous one because here the nonlocal entanglement between the cavity photon and photonic band photons appears.
4. Conclusions
In this paper, we have studied the parametric amplification of a quantum vacuum in the optomechanical cavity interacting with a one-dimensional photonic crystal. The effective non-Hermitian Floquet–Liouvillian has been derived from a Heisenberg equation of the total system by using the Floquet method and the Brillouin–Wigner–Feshbach projection method, where we have taken into account a microscopic dissipation mechanism in terms of the energy-dependent self energy. The non-Hermitian effective Floquet–Liouvillian reveals the competing instabilities of parametric amplification and dissipation due to the virtual transition and the resonance singularity, respectively. The emergence of the stationary mode has been identified as a result of the balance between the two instabilities, where the eigenmode of the Liouvillian is represented by the Bogoliubov transformation. The photonic band edge effect is prominent when the cavity mode frequency is close to the band edge. In this case, the indirect coupling between the cavity mode and photonic band via the virtual transition of the cavity modes yields the nonlocal stationary mode, which is represented by the multimode-Bogoliubov tranformation of the cavity mode and photonic band.
Lastly, we would emphasize a practical advantage of the present model for the observation of the DCE. A major obstacle for the observation of the DCE is the difficulty to move the boundary with almost twice the cavity frequency, . However, the results of the preceding section indicate that we may use the lower frequency pump field to induce the multimode parametric amplification, which is attributed to the indirect virtual coupling between the cavity mode and the photonic band while suppressing the direct dissipation to the photonic band. In Figure 6, we show the frequency level scheme of , , , and for that situation. First, in order to suppress the direct dissipation to the photonic band, the cavity mode frequency must be outside of the photonic band:
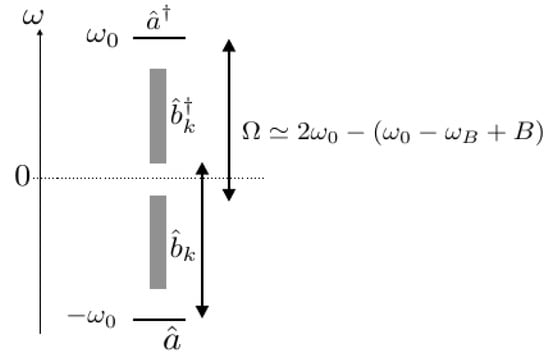
Figure 6.
Floquet–Liouvillian level scheme in a situation direct dissipation to the photonic band is suppressed and multimode parametric amlification is induced with the external driving frequency much smaller than .
Under this condition, when the pumping field is taken as
the creation (annihilation) cavity mode is in resonance with the annihilation (creation) mode of the photonic band so that the multimode parametric amplification happens. It is clear from (21) and (22) that the multimode parametric amplification happens for , far smaller than . Therefore, the major obstacle can be diminished.
Very recently, a method to reduce the mirror frequency for the DCE has been proposed to take advantage of a nonlinear interaction of the quantized mirror motion and the cavity photon mode [36,37], where the strong nonlinear mixing between the mirror motion and cavity mode is assumed to be represented by the dressed state representation. Our proposal provides an alternative method for the reduction of the pump frequency to induce the multimode parametric amplification by using a finite bandwidth photonic band, i.e., a control of the dissipation process. It is considered that the characteristics of the emitted photon are varied according to different types of the DCE emission processes.
In the present work, we have found three different types of the stationary modes. One is a completely stationary state well below the two bifurcation thresholds, where a cavity squeezed vacuum state is associated with a localized virtual photon cloud of the photonic band, and the periodic Rabi oscillation happens between the cavity squeezed vacuum and the virtual photon cloud. The second one is the multimode DCE, where the stationary spontaneous photon emission to the photonic band happens with the two-photon entanglement between the cavity mode and the photonic band. The third one is the ordinary DCE, where an entangled cavity photon pair is emitted to the photonic band. We can observe the two-photon entanglement of the emitted photons by a quantum correlation observation, such as the homodyne detection method [14,59]. We will show the study of the real-time dynamics of these photon emission processes in a forthcoming paper.
Author Contributions
S.T. conceived the idea, developed the theory, and performed the theoretical analyses; S.T. and K.K. discussed the results and contributed to the final manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by JSPS KAKENHI grant Nos. JP18K03496, JP17K05585, JP16H04003, and JP16K05481.
Acknowledgments
We are very grateful to Tomio Petrosky, Roberto Passante, Yosuke Kayanuma, Kohji Mizoguchi, Ken-ichi Noba, Savannah Garmon, and Michelangelo Domina for fruitful discussions.
Conflicts of Interest
The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, and in the decision to publish the results.
Appendix A. Floquet–Liouvillian Complex Eigenvalue Problem and Effective Operator
In this section, we briefly review the Floquet method according to Refs. [50,51,63], and derive the effective Floquet–Liouvillian given in (12). The composite space is composed of the coordinate space and the temporal space of periodic functions in time with period T [51]. In -space, any periodic function of t is represented as a vector , where the time basis is an eigenstate of a time operator , and the conjugate operator is given by . The eigenstate of is given by
where , satisfying
The time basis is given by the transformation of
Together with the basis of -space, the complete orthonormal basis set in the -space is formed by or in terms of the time- or Floquet-mode-representations, respectively, where denotes a vector in the -space. In this paper, we have abbreviated as and . These bases satisfy the complete-orthonormality
in terms of , or
in terms of basis set.
Using the transform of (A1), the complex eigenvalue problem of the Floquet–Liouvillian
is transformed to time-independent eigenvalue problem in terms of the Floquet-mode representation. The matrix structure of is given by
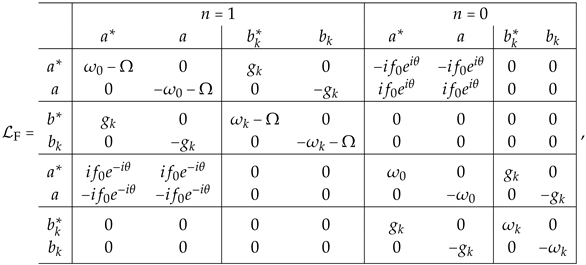 where we show the matrix only for the and Floquet modes and a particular k mode of the photonic band, for simplicity. It is found that the virtual transition interactions couples the creation and annihilation modes of the cavity belonging to a next neighbor Floquet modes:
which make non-Hermitian.
where we show the matrix only for the and Floquet modes and a particular k mode of the photonic band, for simplicity. It is found that the virtual transition interactions couples the creation and annihilation modes of the cavity belonging to a next neighbor Floquet modes:
which make non-Hermitian.

Under the condition of
which is satisfied for the narrow photonic band and small external amplitude, we can restrict ourselves to space. Using the projection operators [56] of
we have reduced the complex eigenvalue problem of the total Floquet–Liouvillian (A6) to an eigenvalue problem of an effective Floquet Liouvillian in terms of the cavity modes of as
where the effective Floquet–Liouvillian is defined by [21,49,56,61,62]
The effective Floquet–Liouvillian is represented by a two-by-two matrix in terms of
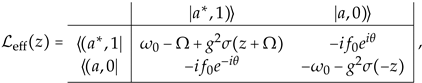 where the self-energy is analytically obtained for the interaction of the cavity mode with the one-dimensional photonic crystal as
where the self-energy is analytically obtained for the interaction of the cavity mode with the one-dimensional photonic crystal as
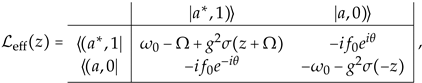
It should be noted that the effective Floquet–Liouvillian depends on its eigenvalue so that the eigenvalue problem should be solved in a self-consistent manner so as to correctly describe the microscopic dissipation mechanism. The eigenvalues have been obtained by solving the dispersion Equation (16), which has been derived from (A11).
References
- Milonni, P.W. The Quantum Vacuum: An Introduction to Quantum Electrodynamics; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Lamb, W.E.; Retherford, R.C. Fine Structure of the Hydrogen Atom by a Microwave Method. Phys. Rev. 1947, 72, 241–243. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Quantum Theory of the Emission and Absorption of Radiation. Proc. R. Soc. Ser. A 1927, 114, 243–265. [Google Scholar] [CrossRef]
- Weisskopf, V.; Wigner, E. Berechnung der natürlichen Linienbreite auf Grund der Diracschen Lichttheorie. Z. Phys. 1930, 63, 54–73. [Google Scholar] [CrossRef]
- Casimir, H.B.G.; Polder, D. The influence of retardation on the London-van der Waals forces. Phys. Rev. 1948, 73, 360–372. [Google Scholar] [CrossRef]
- Lamoreaux, S.K. Demonstration of the casimir force in the 0.6 to 6 µm range. Phys. Rev. Lett. 1997, 78, 5–8. [Google Scholar] [CrossRef]
- Moore, G.T. Quantum Theory of the Electromagnetic Field in a Variable-Length One-Dimensional Cavity. J. Math. Phys. 1970, 11, 2679–2691. [Google Scholar] [CrossRef]
- Fulling, S.A.; Davies, P.C.W.; Penrose, R. Radiation from a moving mirror in two-dimensional space-time: Conformal anomaly. Proc. R. Soc. Lond. Ser. A 1976, 348, 393–414. [Google Scholar] [CrossRef]
- Dodonov, V.V. Current status of the dynamical Casimir effect. Phys. Scr. 2010, 82. [Google Scholar] [CrossRef]
- Nation, P.D.; Johansson, J.R.; Blencowe, M.P.; Nori, F. Colloquium: Stimulating uncertainty: Amplifying the quantum vacuum with superconducting circuits. Rev. Mod. Phys. 2012, 84, 1–24. [Google Scholar] [CrossRef]
- Wilson, C.M.; Johansson, G.; Pourkabirian, A.; Simoen, M.; Johansson, J.R.; Duty, T.; Nori, F.; Delsing, P. Observation of the dynamical Casimir effect in a superconducting circuit. Nature 2011, 479, 376–379. [Google Scholar] [CrossRef]
- Lähteenmäki, P.; Paraoanu, G.S.; Hassel, J.; Hakonen, P.J. Dynamical Casimir effect in a Josephson metamaterial. Proc. Natl. Acad. Sci. USA 2013, 110, 4234–4238. [Google Scholar] [CrossRef]
- Carmichael, H.J. Statistical Methods in Quantum Optics 2: Non-Classical Fields; Theoretical and Mathematical Physics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Walls, D.F.; Milburn, G.J. Quantum Optics; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Mollow, B.; Glauber, R. Quantum Theory of Parametric Amplification. I. Phys. Rev. 1986, 160, 1076–1096. [Google Scholar] [CrossRef]
- Wu, L.A.; Xiao, M.; Kimble, H.J. Squeezed states of light from an optical parametric oscillator. J. Opt. Soc. Am. B 1987, 4, 1465. [Google Scholar] [CrossRef]
- Kohler, S.; Dittrich, T.; Hänggi, P. Floquet-Markovian description of the parametrically driven, dissipative harmonic quantum oscillator. Phys. Rev. E 1997, 55, 300–313. [Google Scholar] [CrossRef]
- Bender, C.M.; Dorey, P.E.; Dunning, C.; Fring, A.; Hook, D.W.; Jones, H.F.; Kuzhel, S.; Lévai, G.; Tateo, R. PT Symmetry; World Scientific: London, UK, 2019. [Google Scholar] [CrossRef]
- Moiseyev, N. Non-Hermitian Quantum Mechanics; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Prigogine, I. Time, structure, and fluctuations (Nobel Lecture, December 8, 1977). In Nobel Lectures in Chemistry 1971–1980; World Scientific Publishing Co.: Singapore, 1993. [Google Scholar]
- Petrosky, T.; Prigogine, I.; Tasaki, S. Quantum theory of non-integrable systems. Physica A 1991, 173, 175–242. [Google Scholar] [CrossRef]
- Prigogine, I. Dissipative processes in quantum theory. Phys. Rep. 1992, 219, 93–108. [Google Scholar] [CrossRef]
- Prigogine, I. Laws of nature, probability and time symmetry breaking. Physica A 1999, 263, 528–539. [Google Scholar] [CrossRef]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Atom-Photon Interactions: Basic Processes and Applications; Wiley Interscience: New York, NY, USA, 1998. [Google Scholar]
- Collett, M.J.; Gardiner, C.W. Squeezing of intracavity and traveling-wave light fields produced in parametric amplification. Phys. Rev. A 1984, 30, 1386–1391. [Google Scholar] [CrossRef]
- Ciuti, C.; Carusotto, I. Input-output theory of cavities in the ultrastrong coupling regime: The case of time-independent cavity parameters. Phys. Rev. A 2006, 74, 033811. [Google Scholar] [CrossRef]
- Carmichael, H.J. Spectrum of squeezing and photocurrent shot noise: A normally ordered treatment. J. Opt. Soc. Am. B 1987, 4, 1588–1603. [Google Scholar] [CrossRef]
- De Liberato, S.; Gerace, D.; Carusotto, I.; Ciuti, C. Extracavity quantum vacuum radiation from a single qubit. Phys. Rev. A 2009, 80, 053810. [Google Scholar] [CrossRef]
- John, S.; Wang, J. Quantum electrodynamics near a photonic band gap: Photon bound states and dressed atoms. Phys. Rev. Lett. 1990, 64, 2418–2421. [Google Scholar] [CrossRef] [PubMed]
- John, S.; Quang, T. Spontaneous emission near the edge of a photonic band gap, 1994. Phys. Rev. A 1994, 50, 1764–1769. [Google Scholar] [CrossRef] [PubMed]
- De Liberato, S. Light-matter decoupling in the deep strong coupling regime: The breakdown of the purcell effect. Phys. Rev. Lett. 2014, 112, 016401. [Google Scholar] [CrossRef] [PubMed]
- Calajò, G.; Rizzuto, L.; Passante, R. Control of spontaneous emission of a single quantum emitter through a time-modulated photonic-band-gap environment. Phys. Rev. A 2017, 96, 023802. [Google Scholar] [CrossRef]
- Rybin, M.V.; Zherzdev, A.V.; Feoktistov, N.A.; Pevtsov, A.B. Effect of photonic crystal stop-band on photoluminescence of a-Si1-x Cx: H. Phys. Rev. B 2017, 95, 165118. [Google Scholar] [CrossRef]
- Xiang, Z.L.; Ashhab, S.; You, J.Q.; Nori, F. Hybrid quantum circuits: Superconducting circuits interacting with other quantum systems. Rev. Mod. Phys. 2013, 85, 623–653. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Settineri, A.; Macrì, V.; Garziano, L.; Di Stefano, O.; Nori, F.; Savasta, S. Conversion of mechanical noise into correlated photon pairs: Dynamical Casimir effect from an incoherent mechanical drive. Phys. Rev. A 2019, 100, 022501. [Google Scholar] [CrossRef]
- Macrì, V.; Ridolfo, A.; Di Stefano, O.; Kockum, A.F.; Nori, F.; Savasta, S. Nonperturbative Dynamical Casimir Effect in Optomechanical Systems: Vacuum Casimir-Rabi Splittings. Phys. Rev. X 2018, 8, 11031. [Google Scholar] [CrossRef]
- de M. e Souza, R.; Impens, F.; Neto, P.A.M. Microscopic dynamical Casimir effect. Phys. Rev. A 2018, 97, 032513. [Google Scholar] [CrossRef]
- Farías, M.B.; Fosco, C.D.; Lombardo, F.C.; Mazzitelli, F.D. Motion induced radiation and quantum friction for a moving atom. Phys. Rev. D 2019, 100, 036013. [Google Scholar] [CrossRef]
- Petrosky, T.; Ordonez, G.; Prigogine, I. Quantum transitions and nonlocality. Phys. Rev. A 2000, 62, 042106. [Google Scholar] [CrossRef]
- Karpov, E.; Prigogine, I.; Petrosky, T.; Pronko, G. Friedrichs model with virtual transitions. Exact solution and indirect spectroscopy. J Math. Phys. 2000, 41, 118–131. [Google Scholar] [CrossRef]
- Petrosky, T.; Ordonez, G.; Prigogine, I. Space-time formulation of quantum transitions. Phys. Rev. A 2001, 64, 062101. [Google Scholar] [CrossRef]
- Ordóez, G.; Petrosky, T.; Karpov, E.; Prigogine, I. Explicit construction of a time superoperator for quantum unstable systems. Chaos Solitons Fractals 2001, 12, 2591–2601. [Google Scholar] [CrossRef]
- Hatano, N.; Nelson, D.R. Vortex pinning and non-Hermitian quantum mechanics. Phys. Rev. B 1997, 56, 8651–8673. [Google Scholar] [CrossRef]
- Bender, C.M.; Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 1998, 80, 5243–5246. [Google Scholar] [CrossRef]
- Tanaka, S.; Garmon, S.; Petrosky, T. Nonanalytic enhancement of the charge transfer from adatom to one-dimensional semiconductor superlattice and optical absorption spectrum. Phys. Rev. B 2006, 73, 115340. [Google Scholar] [CrossRef]
- Tanaka, S.; Garmon, S.; Ordonez, G.; Petrosky, T. Electron trapping in a one-dimensional semiconductor quantum wire with multiple impurities. Phys. Rev. B 2007, 76, 153308. [Google Scholar] [CrossRef]
- Tanaka, S.; Passante, R.; Fukuta, T.; Petrosky, T. Nonperturbative approach for the electronic Casimir-Polder effect in a one-dimensional semiconductor. Phys. Rev. A 2013, 88, 022518. [Google Scholar] [CrossRef]
- Tanaka, S.; Garmon, S.; Kanki, K.; Petrosky, T. Higher-order time-symmetry-breaking phase transition due to meeting of an exceptional point and a Fano resonance. Phys. Rev. A 2016, 94, 022105. [Google Scholar] [CrossRef]
- Sambe, H. Steady states and quasienergies of a quantum-mechanical system in an oscillating field. Phys. Rev. A 1973, 7, 2203–2213. [Google Scholar] [CrossRef]
- Grifoni, M.; Hänggi, P. Driven quantum tunneling. Phys. Rep. 1998, 304, 229–354. [Google Scholar] [CrossRef]
- Feshbach, H. A unified theory of nuclear reactions. II. Ann. Phys. 1962, 19, 287–313. [Google Scholar] [CrossRef]
- Rotter, I. A non-Hermitian Hamilton operator and the physics of open quantum systems. J. Phys. A 2009, 42, 153001. [Google Scholar] [CrossRef]
- Hatano, N. Equivalence of the effective Hamiltonian approach and the Siegert boundary condition for resonant states. Fortschr. Phys. 2013, 61, 238–249. [Google Scholar] [CrossRef]
- Kanki, K.; Garmon, S.; Tanaka, S.; Petrosky, T. Exact description of coalescing eigenstates in open quantum systems in terms of microscopic Hamiltonian dynamics. J. Math. Phys. 2017, 58, 092101. [Google Scholar] [CrossRef]
- Yamane, H.; Tanaka, S. Ultrafast Dynamics of High-Harmonic Generation in Terms of Complex Floquet Spectral Analysis. Symmetry 2018, 10, 313. [Google Scholar] [CrossRef]
- Law, C.K. Effective Hamiltonian for the radiation in a cavity with a moving mirror and a time-varying dielectric medium. Phys. Rev. A 1994, 49, 433–437. [Google Scholar] [CrossRef]
- Law, C.K. Interaction between a moving mirror and radiation pressure: A Hamiltonian formulation. Phys. Rev. A 1995, 51, 2537–2541. [Google Scholar] [CrossRef] [PubMed]
- Loudon, R. The Quantum Theory of Light; OUP Oxford: Oxford, UK, 2000. [Google Scholar]
- Cohen-Tannoudji, C.; Dupont-Roc, J.; Grynberg, G. Photons and Atoms: Introduction to Quantum Electrodynamics; Wiley-VCH: Hoboken, NJ, USA, 1989. [Google Scholar]
- Fukuta, T.; Garmon, S.; Kanki, K.; Noba, K.I.; Tanaka, S. Fano absorption spectrum with the complex spectral analysis. Phys. Rev. A 2017, 96, 052511. [Google Scholar] [CrossRef]
- Tanaka, S.; Fukuta, T.; Petrosky, T. Study of Fano Resonance in the Core-Level Absorption Spectrum in Terms of Complex Spectral Analysis. In Fano Resonances in Optics and Microwaves: Physics and Applications; Kamenetskii, E., Sadreev, A., Miroshnichenko, A., Eds.; Springer: Cham, Switzerland, 2018; pp. 261–281. [Google Scholar] [CrossRef]
- Shirley, J.H. Solution of the Schrodinger Equation with a Hamiltonian Periodic in Time. Phys. Rev. 1965, 138, B979. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).