Seasonal Analysis of Silicon Photovoltaic Technology Module †
Abstract
:1. Introduction
2. Methodology
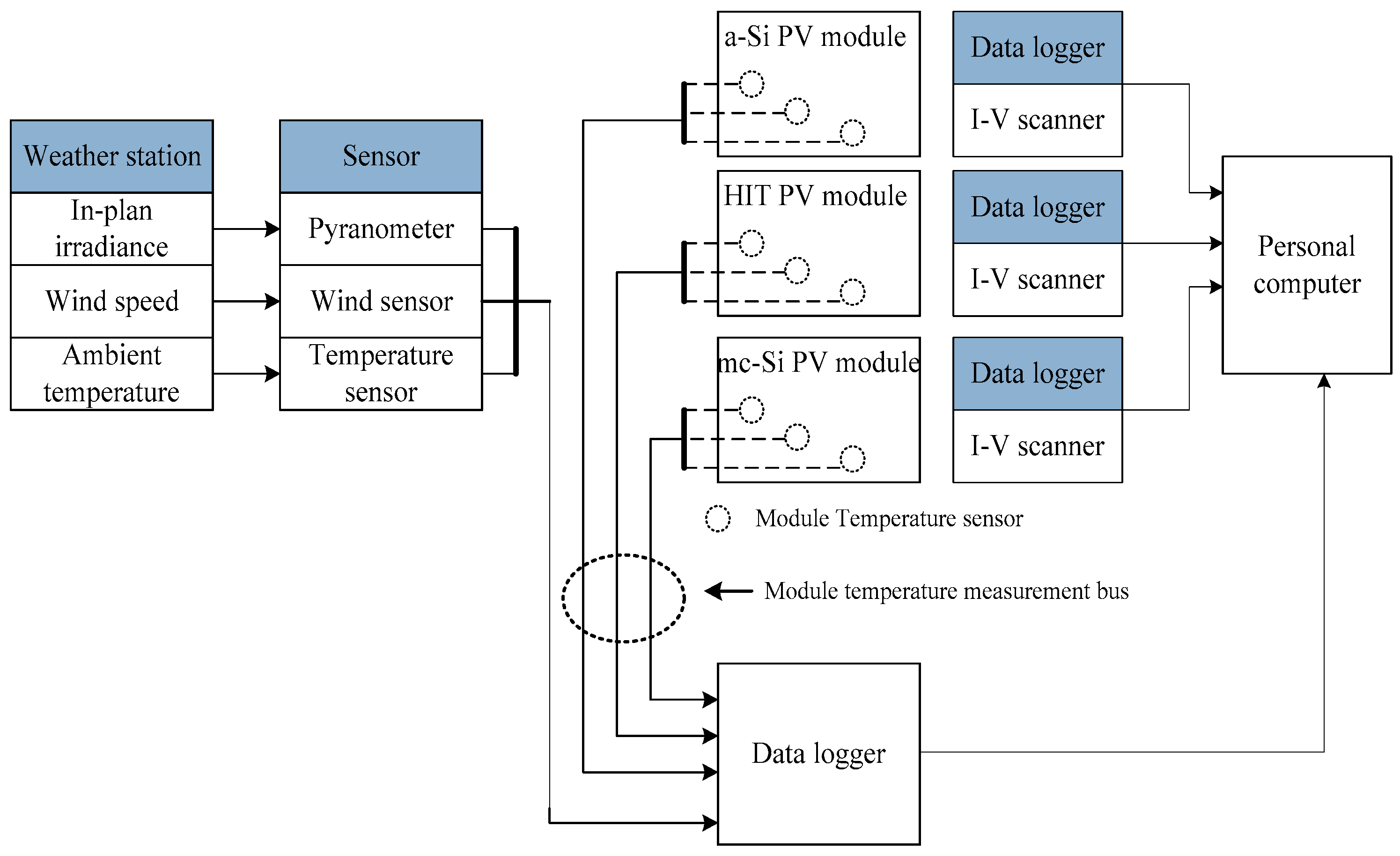
3. Measurement and Experimental Setup
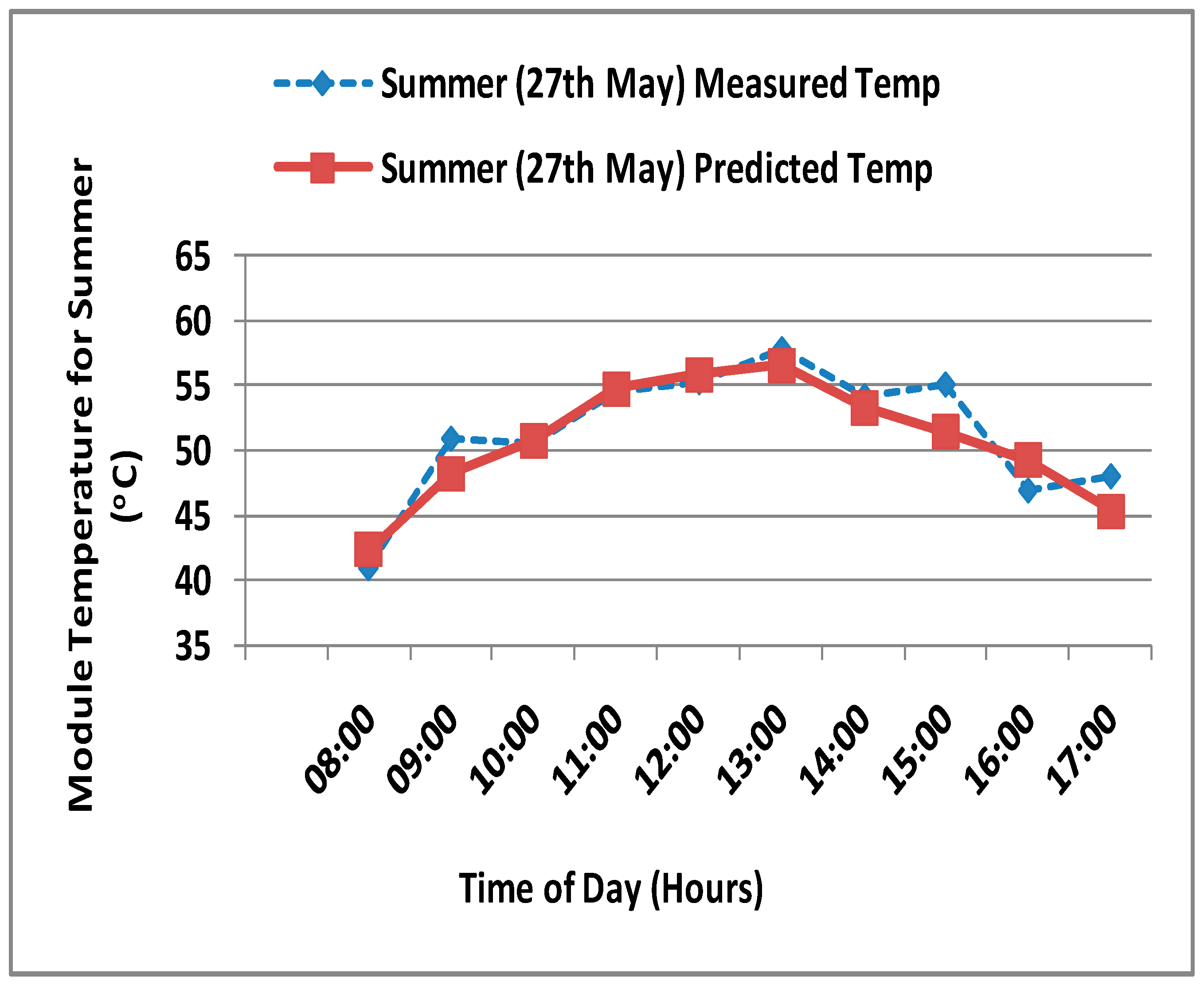
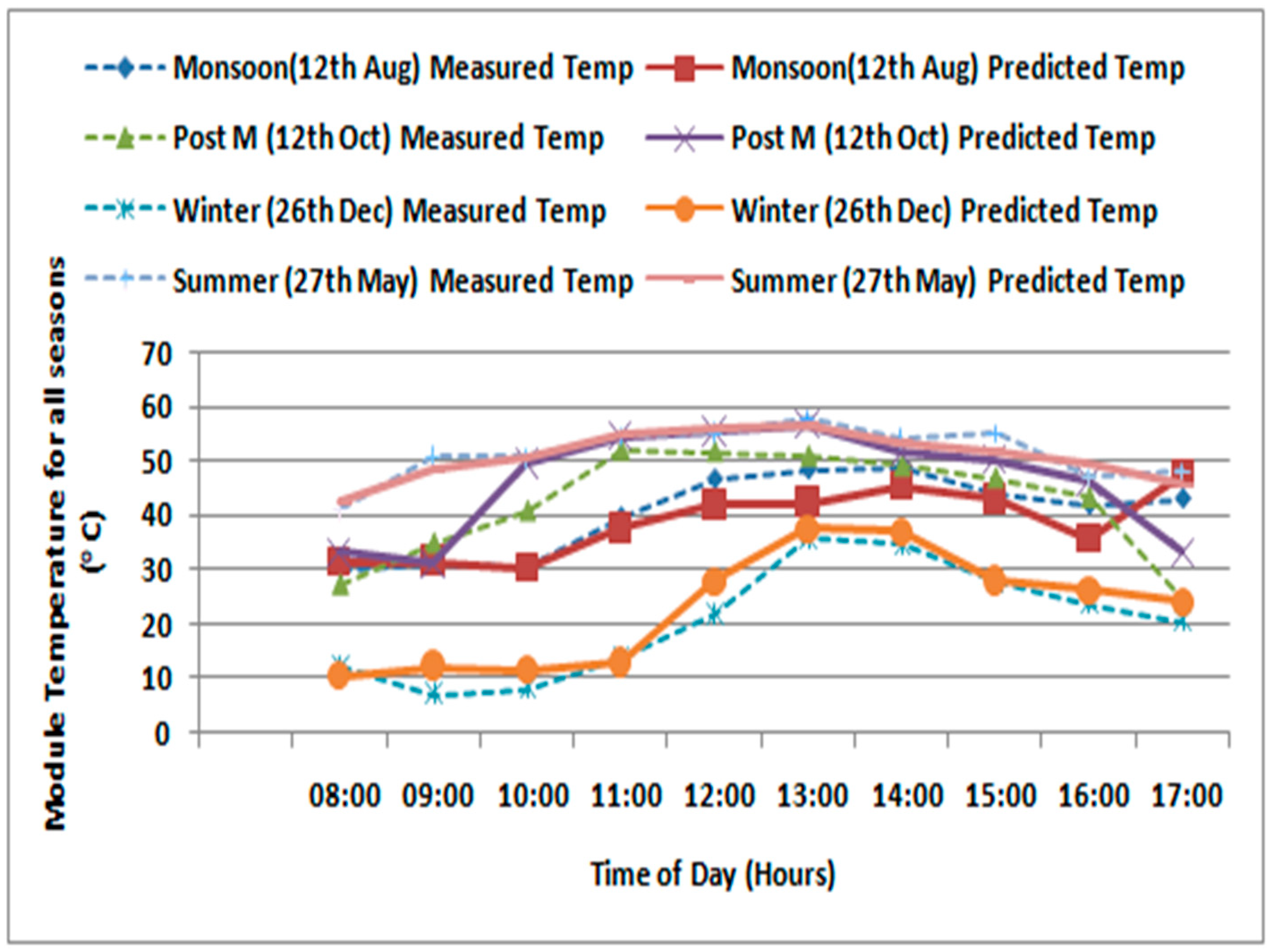
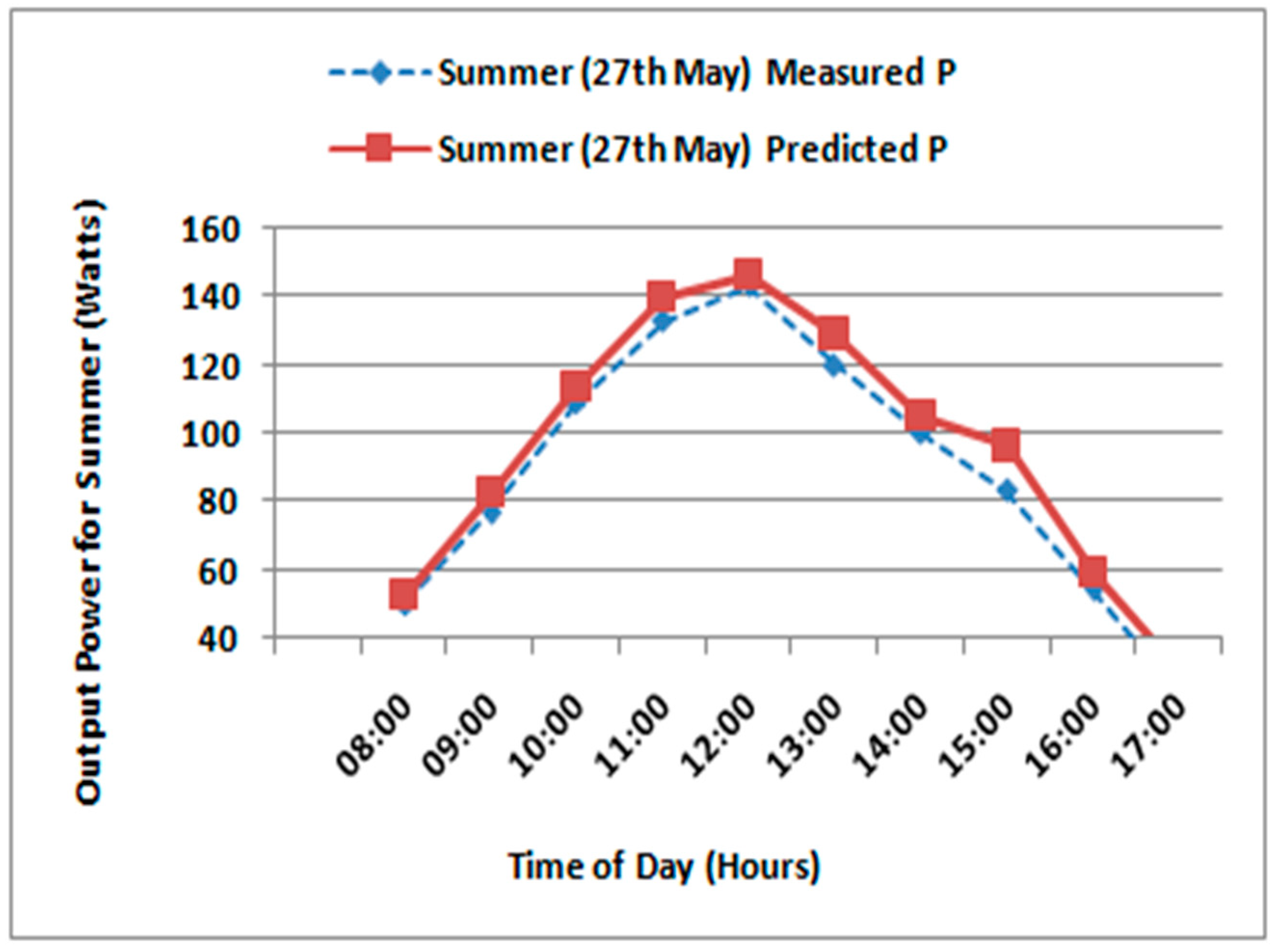
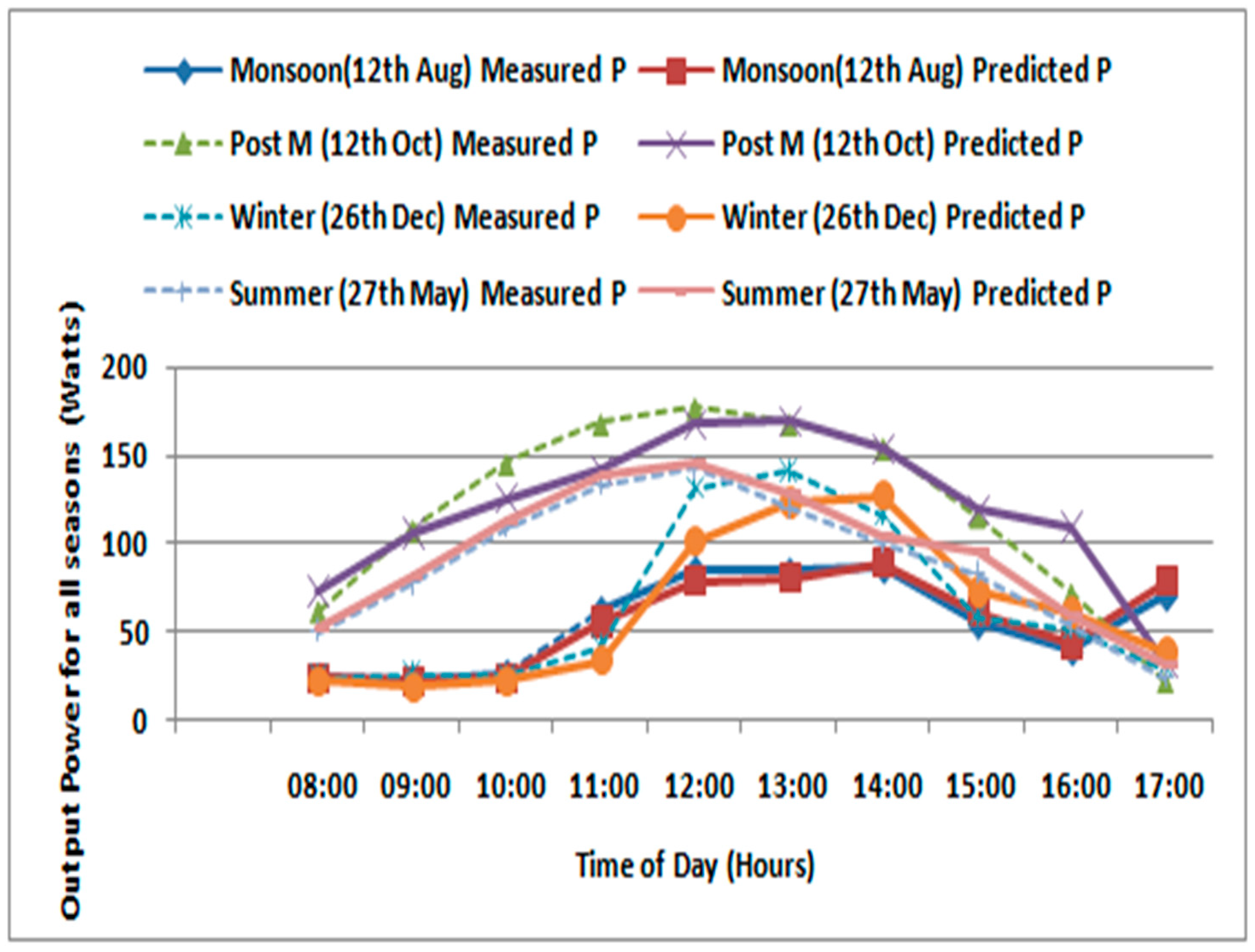
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L.; et al. Solar influence on climate. Rev. Geophys. 2010, 48, 1–53. [Google Scholar]
- Kelkar, R.R. Monsoons elsewhere in the world. In Monsoon Monograph; Government of India, Ministry of Earth Sciences, India Meteorological Department, 2012. Available online: https://rrkelkar.files.wordpress.com/2019/02/kelkar-2012.pdf (accessed on 1 January 2024).
- Prasanna, V. Impact of monsoon rain fall on the total food grain yield over India. J. Earth Syst. Sci. 2014, 123, 1129–1145. [Google Scholar]
- Parthasarathy, B.; Munot, A.A.; Kothawale, D.R. All India monthly and seasonal rain fall series:1871–1993. Theor. Appl. Climatol. 1995, 49, 217–224. [Google Scholar] [CrossRef]
- Hirata, Y.; Tani, T. Output variation of photovoltaic modules with environmental factors. Sol. Energy 1995, 55, 463–468. [Google Scholar] [CrossRef]
- Hirata, Y.; Inasaka, T.; Tani, T. Output variation of photovoltaic modules with environmental factors-II seasonal variation. Sol. Energy 1998, 63, 185–189. [Google Scholar] [CrossRef]
- Gottschalg, R.; Betts, T.R.; Infield, D.G.; Keamey, M.J. Experimental study of variations of the solar spectrum of relevance to thin film solar cells. Sol. Energy Mater. Sol. Cell 2003, 79, 527–537. [Google Scholar] [CrossRef]
- Gottschalg, R.; Infield, D.G.; Kearney, M.J. Influence of environmental conditions on outdoor performance of thin film devices. In Proceedings of the 17th European Photovoltaic Solar Energy Conference, Munich, Germany, 1 October 2001; pp. 796–799. [Google Scholar]
- Gottschalg, R.; Cueto, J.D.; Betts, T.R.; Williams, S.R.; Infield, D.G. Investigating the seasonal performance of amorphous silicon single and multi-junction modules. In Proceedings of the 3rd World Conference, Osaka, Japan, 11–18 May 2003; pp. 2078–2081. [Google Scholar]
- Dirnberger, D.; Blackburn, G.; Muller, B.; Reise, C. On the impact of solar spectral irradiance on the yield of different PV technologies. Sol. Energy Mater. Sol. Cells 2015, 132, 431–442. [Google Scholar] [CrossRef]
- Dirnberger, D.; Muller, B.; Reise, C. On the uncertainty of energetic impact on the yield of different PV technologies due to varying spectral irradiance. Sol. Energy 2015, 111, 82–96. [Google Scholar] [CrossRef]
- Nakada, Y.; Fukushige, S.; Minemoto, T.; Takakura, H. Seasonal variation analysis of the outdoor performance of amorphous Si photovoltaic modules using the contour map. Sol. Energy Mater. Sol. Cells 2009, 93, 334–337. [Google Scholar] [CrossRef]
- Minemoto, T.; Nagae, S.; Takakura, H. Impact of spectral irradiance distribution and temperature on the outdoor performance of amorphous Si photovoltaic modules. Sol. Energy Mater. Sol. Cells 2007, 91, 919–923. [Google Scholar]
- Jawaharlal Nehru National Solar Mission. Ministry of New and Renewable Energy Government of India, 2010; pp. 1–15. Available online: http://www.mnre.gov.in/filemanager/UserFiles/mission_document_JNNSM.pdf (accessed on 20 June 2015).
- Magare, D.; Sastry, O.S.; Gupta, R.; Kumar, A.; Sinha, A. Data Logging Strategy of Photovoltaic (PV Module Test Beds. In Proceedings of the 27th European Photovoltaic Solar Energy Conference (EUPVSEC), Frankfurt, Germany, 24–28 September 2012; pp. 3259–3262. [Google Scholar]
- Magare, D.; Sastry, O.; Gupta, R.; Bora, B.; Singh, Y.; Mohammed, H. Wind Effect Modeling and Analysis for Estimation of Photovoltaic Module Temperature. J. Sol. Energy Eng. 2017, 140, 011008. [Google Scholar] [CrossRef]
- Lekouaghet, B.; Boukabou, A.; Boubakir, C. Estimation of the photovoltaic cells/modules parameters using an improved Rao-based chaotic optimization technique. Energy Convers. Manag. 2021, 229, 113722. [Google Scholar] [CrossRef]
- Ortiz-Conde, A.; Trejo, O.; Garcia-Sanchez, F.J. Direct extraction of solar cell model parameters using optimization methods. In Proceedings of the IEEE Latin America Electron Devices Conference (LAEDC), Mexico, 19–21 April 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Kanekar, K.D.; Agrawal, R.; Magare, D. Different Meta-Heuristic Optimization Techniques and Application in Solar Photovoltaic Field: A Renewable Energy Source. In Optimal Planning of Smart Grid with Renewable Energy Resources; IGI Global: Hershey, PA, USA, 2022; pp. 1–37. [Google Scholar]
- Montalvo-Galicia, F.; Sanz-Pascual, M.T.; Rosales-Quintero, P.; Moreno-Moreno, M. Parameter extraction method for the two-diode solar cell model. In Proceedings of the IEEE 65th International Midwest Symposium on Circuits and Systems (MWSCAS), Fukuoka, Japan, 7–10 August 2022; pp. 1–4. [Google Scholar] [CrossRef]

| Coefficients | Monsoon | Post Monsoon | Winter | Summer |
|---|---|---|---|---|
| Power Coefficient (a1) | −0.0076 | −0.2615 | −0.0113 | −0.0053 |
| Power Coefficient (a2) | 0.0035 | 0.0013 | 0.04166 | 0.003 |
| Irradiance (a3) | 0.024 | 0.0375 | 0.0254 | 0.0309 |
| Ambient temperature (a4) | 1.23 | 1.175 | 1.142 | 1.0422 |
| Wind Speed(a5) | −1.0327 | −2.4569 | −1.3112 | −1.0113 |
| Constant (a6) | −9.8155 | −2.1883 | −1.8169 | −0.5167 |
| Seasons | RMSE of Module Temperature | RMSE of Power |
|---|---|---|
| Monsoon | 3.9026 | 3.6532 |
| Post Monsoon | 4.7126 | 3.7391 |
| Winter | 4.4333 | 3.8425 |
| Summer | 4.9832 | 4.1264 |
| Active Module Area, A (m2) | Module Power PSTC (W) | Temperature Coefficient of Power (%/°C) | Power RMSE by Literature Method | Power RMSE by Proposed Method |
|---|---|---|---|---|
| 1.01 | 160 | −0.49 | 4.68 | 3.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanekar, K.; Burade, P.; Magare, D. Seasonal Analysis of Silicon Photovoltaic Technology Module. Eng. Proc. 2023, 59, 184. https://doi.org/10.3390/engproc2023059184
Kanekar K, Burade P, Magare D. Seasonal Analysis of Silicon Photovoltaic Technology Module. Engineering Proceedings. 2023; 59(1):184. https://doi.org/10.3390/engproc2023059184
Chicago/Turabian StyleKanekar, Krupali, Prakash Burade, and Dhiraj Magare. 2023. "Seasonal Analysis of Silicon Photovoltaic Technology Module" Engineering Proceedings 59, no. 1: 184. https://doi.org/10.3390/engproc2023059184





