A Versatile Deposition Model for Natural and Processed Surfaces
Abstract
:1. Introduction
2. Theory and Methods
2.1. Modeling Interface Growth in the Kardar-Parisi-Zhang Universality Class
- is time under the derivative of the height function;
- is the surface tension, or diffusion term smoothing the interface,
- is a nonlinear term capturing the local curvature of the interface, promoting the growth in regions with significant local curvature;
- is the Gaussian white noise term representing random fluctuations.
2.2. Random Versus Ballistic Deposition Models
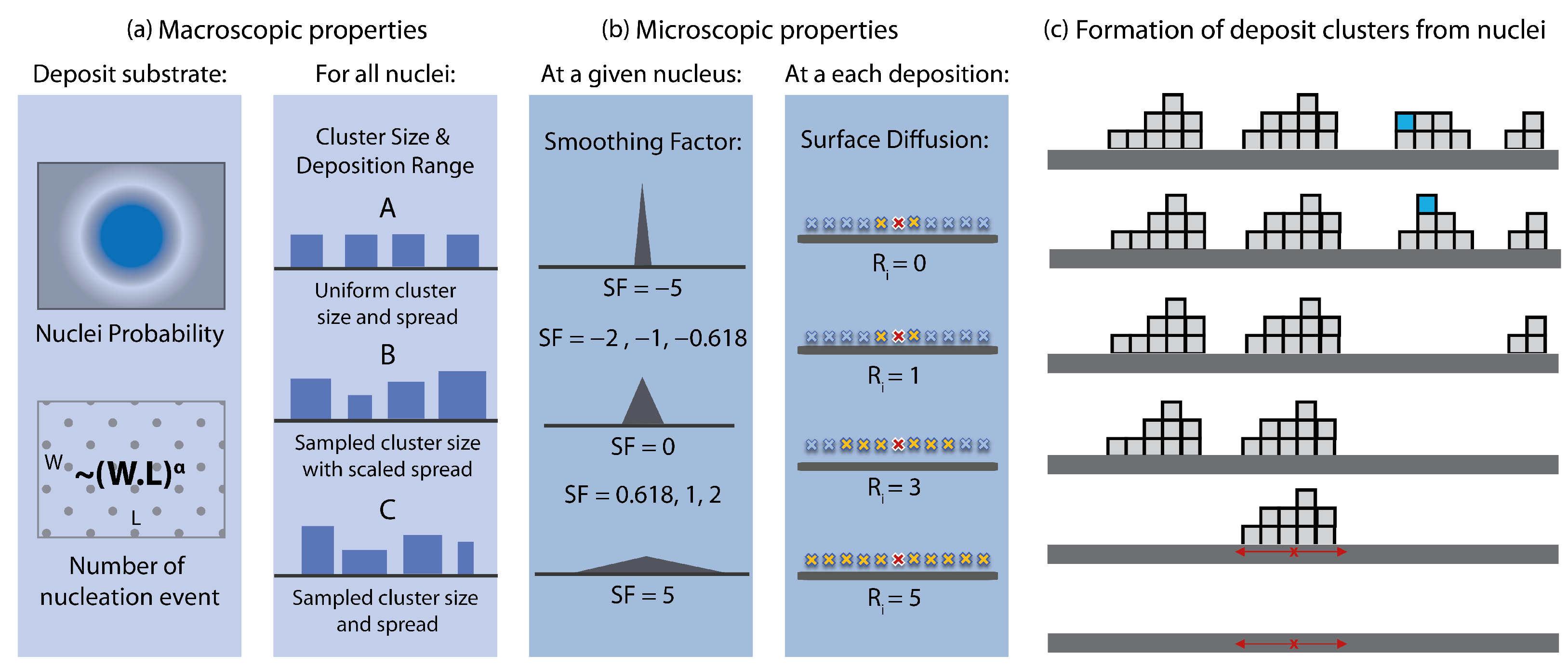
2.3. Proposed Top-Down Modelling Approach
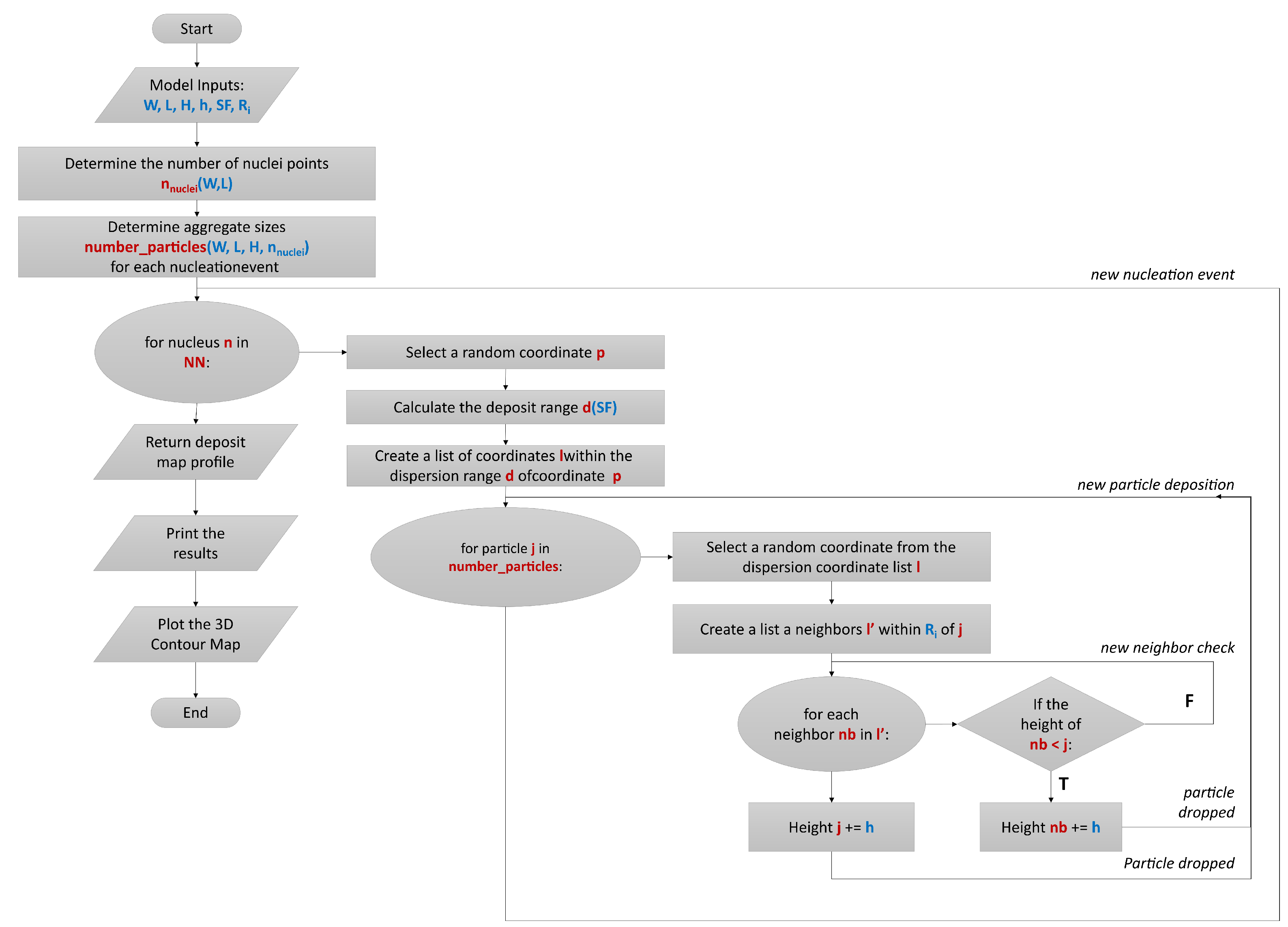
2.3.1. Algorithm
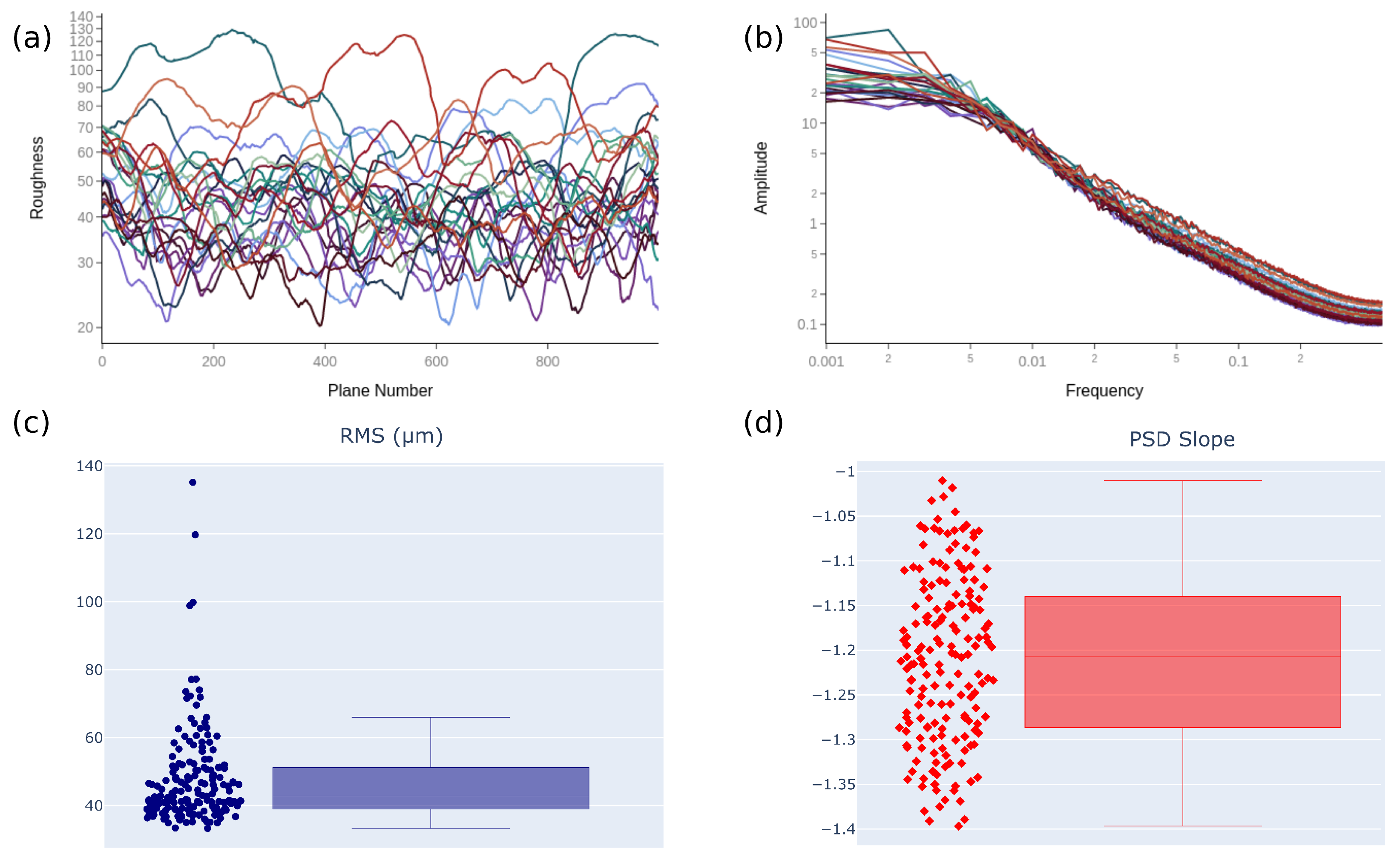
2.3.2. Proof-of-Concept Study and the Target Library
3. Results
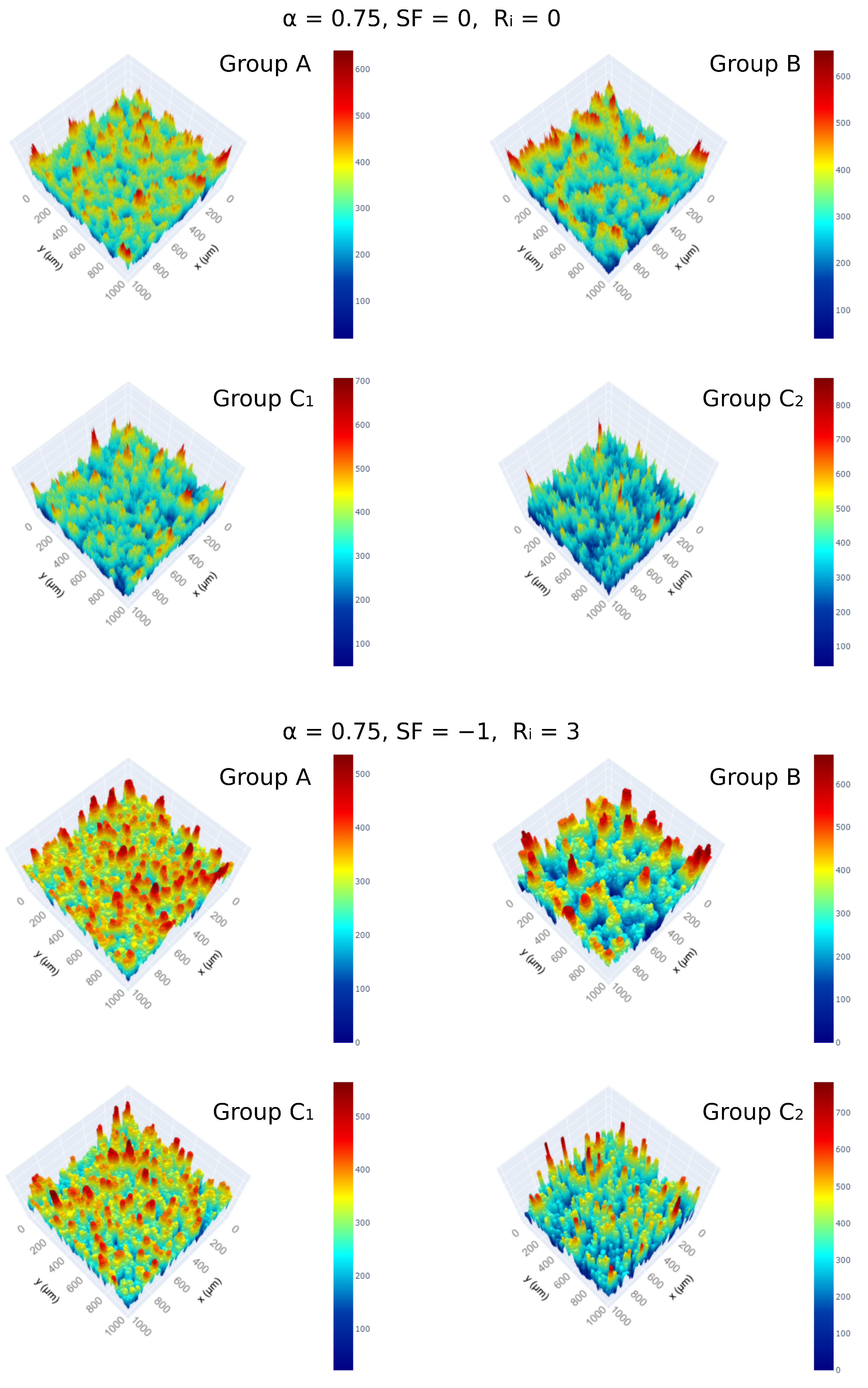
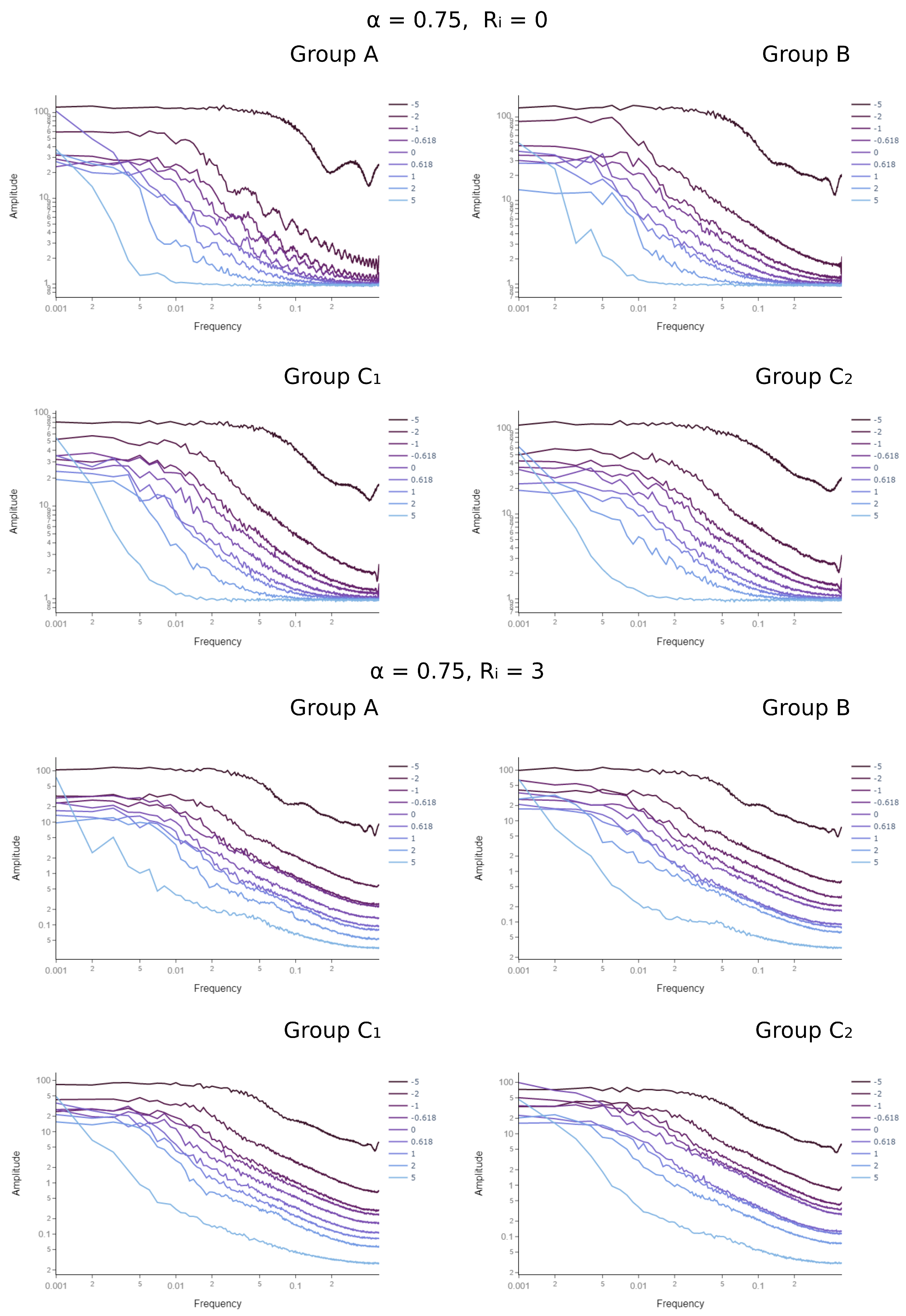
3.1. Impact of Model Parameters on the Generated Deposit Morphology
3.2. Generation of Porous Structures
3.3. Proof-of-Concept: Urea Deposit Formation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BD | Ballistic Deposition |
| FFT | Fast Fourier Transform |
| KPZ | Kardar–Parisi–Zhang |
| PSD | Power Spectral Density |
| RD | Random Deposition |
| RMS | Root Mean Square |
| SCR | Selective Catalytic Reduction |
| SF | Smoothing Factor |
| UWS | Urea Water Solution |
References
- Ates, C.; Börnhorst, M.; Koch, R.; Eck, M.; Deutschmann, O.; Bauer, H.J. Morphological characterization of urea derived deposits in SCR systems. Chem. Eng. J. 2021, 409, 128230. [Google Scholar] [CrossRef]
- Lehnen, C.; Lu, T.M. Morphological evolution in ballistic deposition. Phys. Rev. B—Condens. Matter Mater. Phys. 2010, 82, 085437. [Google Scholar] [CrossRef]
- Cagnetta, F.; Evans, M.R.; Marenduzzo, D. Kinetic roughening in active interfaces. EPJ Web. Conf. 2020, 230, 00001. [Google Scholar] [CrossRef]
- Krapivsky, P.L.; Redner, S. Birds on a wire. J. Stat. Mech. Theory Exp. 2022, 2022, 103405. [Google Scholar] [CrossRef]
- Giri, A.; Tarafdar, S.; Gouze, P.; Dutta, T. Fractal pore structure of sedimentary rocks: Simulation in 2-d using a relaxed bidisperse ballistic deposition model. J. Appl. Geophys. 2012, 87, 40–45. [Google Scholar] [CrossRef]
- Peng, C.K.; Buldyrev, S.; Goldberger, A.; Havlin, S.; Sciortino, F.; Simons, M.; Stanley, H. Fractal landscape analysis of DNA walks. Phys. A Stat. Mech. Its Appl. 1992, 191, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Clay, M.P.; Simányi, N.J. Rényi’s parking problem revisited. Stochastics Dyn. 2016, 16, 1660006. [Google Scholar] [CrossRef]
- Vold, M.J. Computer simulation of floc formation in a colloidal suspension. J. Colloid Sci. 1963, 18, 684–695. [Google Scholar] [CrossRef]
- Meakin, P.; Ramanlal, P.; Sander, L.M.; Ball, R.C. Ballistic deposition on surfaces. Phys. Rev. A 1986, 34, 5091–5103. [Google Scholar] [CrossRef]
- Meakin, P. Ballistic deposition onto inclined surfaces. Phys. Rev. A 1988, 38, 994–1004. [Google Scholar] [CrossRef]
- Poxson, D.J.; Mont, F.W.; Schubert, M.F.; Kim, J.K.; Schubert, E.F. Quantification of porosity and deposition rate of nanoporous films grown by oblique-angle deposition. Appl. Phys. Lett. 2008, 93, 2981690. [Google Scholar] [CrossRef]
- Grüner, C.; Grüner, S.; Mayr, S.G.; Rauschenbach, B. Avoiding Anisotropies in On-Lattice Simulations of Ballistic Deposition. Phys. Status Solidi 2021, 258, 2000036. [Google Scholar] [CrossRef]
- Meakin, P.; Jullien, R. Spatially correlated ballistic deposition on one- and two-dimensional surfaces. Phys. Rev. A 1990, 41, 983–993. [Google Scholar] [CrossRef] [PubMed]
- Wolf, D.E.; Villain, J. Growth with Surface Diffusion. Europhys. Lett. 1990, 13, 389. [Google Scholar] [CrossRef]
- Meakin, P.; Jullien, R. Ballistic deposition with sticky and non-sticky particles. Phys. A Stat. Mech. Its Appl. 1991, 175, 211–221. [Google Scholar] [CrossRef]
- Ermak, D.L.; Buckholz, H. Numerical integration of the Langevin equation: Monte Carlo simulation. J. Comput. Phys. 1980, 35, 169–182. [Google Scholar] [CrossRef]
- El-Nashar, H.F.; Wang, W.; Cerdeira, H.A. Ballistic deposition model for multiple species with next nearest-neighbour interactions in (2 + 1)-dimensions. Surf. Sci. 1997, 391, 1–10. [Google Scholar] [CrossRef]
- Wang, W.; Cerdeira, H.A. Surface growth of two kinds of particle deposition models. Phys. Rev. E 1995, 52, 6308–6313. [Google Scholar] [CrossRef] [PubMed]
- Pellegrini, Y.P.; Jullien, R. Roughening transition and percolation in random ballistic deposition. Phys. Rev. Lett. 1990, 64, 1745–1748. [Google Scholar] [CrossRef]
- El-Nashar, H.F.; Cerdeira, H.A. Dynamic scaling in a ballistic deposition model for a binary system. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2000, 61, 6149–6155. [Google Scholar] [CrossRef]
- Horowitz, C.M.; Monetti, R.A.; Albano, E.V. Competitive growth model involving random deposition and random deposition with surface relaxation. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2001, 63, 066132. [Google Scholar] [CrossRef] [PubMed]
- Das, S.K.; Banerjee, D.; Roy, J.N. Stochastic Study of Random-Ballistic Competitive Growth Model in 2+1 Dimension and Related Scaling Exponents. J. Inst. Eng. Ser. D 2023, 104, 777–784. [Google Scholar] [CrossRef]
- Karmakar, R.; Dutta, T.; Lebovka, N.; Tarafdar, S. Effect of surface roughness on the bulk properties of simulated porous media. Phys. A: Stat. Mech. Its Appl. 2005, 348, 236–244. [Google Scholar] [CrossRef]
- Forgerini, F.L.; Figueiredo, W. Random deposition of particles of different sizes. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2009, 79, 041602. [Google Scholar] [CrossRef] [PubMed]
- Ebrahiminejad, Z.; Masoudi, S.F.; Dariani, R.S.; Jahromi, S.S. Thin film growth by deposition of randomly shaped clusters. J. Chem. Phys. 2012, 137, 4755956. [Google Scholar] [CrossRef] [PubMed]
- Sharafedini, E.; Hamzehpour, H.; Masoudi, S.F.; Sahimi, M. Electrical conductivity of the films grown by ballistic deposition of rodlike particles. J. Appl. Phys. 2015, 118, 4936548. [Google Scholar] [CrossRef]
- Madadi, Z.; Hassanibesheli, F.; Esmaeili, S.; Hedayatifar, L.; Masoudi, A.A. Surface growth by cluster particles: Effects of diffusion and cluster’s shape. J. Cryst. Growth 2017, 480, 56–61. [Google Scholar] [CrossRef]
- Hosseinabadi, S.; Masoudi, A.A. Random deposition with a power-law noise model: Multiaffine analysis. Phys. Rev. E 2019, 99, 012130. [Google Scholar] [CrossRef]
- Das, S.K.; Banerjee, D.; Roy, J.N. Particle shape-induced correlation effect in random deposition in 1 + 1 dimension and related effect in ballistic deposition. Surf. Rev. Lett. 2021, 28, 2050043. [Google Scholar] [CrossRef]
- Comets, F.; Dalmau, J.; Saglietti, S. Scaling limit of the heavy tailed ballistic deposition model with p-sticking. Ann. Probab. 2023, 51, 1870–1931. [Google Scholar] [CrossRef]
- Rahimi, M.; Hosseinabadi, S.; Masoudi, A. Geometrical exponents of contour loops on ballistic deposition model with power-law distributed noise. Chaos Solitons Fractals 2023, 177, 114249. [Google Scholar] [CrossRef]
- Hu, G.; Orkoulas, G.; Christofides, P.D. Regulation of film thickness, surface roughness and porosity in thin film growth using deposition rate. Chem. Eng. Sci. 2009, 64, 3903–3913. [Google Scholar] [CrossRef]
- Robledo, A.; Grabill, C.N.; Kuebler, S.M.; Dutta, A.; Heinrich, H.; Bhattacharya, A. Morphologies from slippery ballistic deposition model: A bottom-up approach for nanofabrication. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2011, 83, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Banerjee, K.; Shamanna, J.; Ray, S. Surface morphology of a modified ballistic deposition model. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 90, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Aarão Reis, F.D. Kinetic roughening and porosity scaling in film growth with subsurface lateral aggregation. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2015, 91, 1–9. [Google Scholar] [CrossRef]
- Mal, B.; Ray, S.; Shamanna, J. Surface properties and scaling behavior of a generalized ballistic deposition model. Phys. Rev. E 2016, 93, 3–8. [Google Scholar] [CrossRef] [PubMed]
- Kartha, M.J. Surface morphology of ballistic deposition with patchy particles and visibility graph. Phys. Lett. A 2017, 381, 556–560. [Google Scholar] [CrossRef]
- Oliveira Filho, J.S.; Oliveira, T.J.; Redinz, J.A. Surface and bulk properties of ballistic deposition models with bond breaking. Phys. A Stat. Mech. Its Appl. 2013, 392, 2479–2486. [Google Scholar] [CrossRef]
- Nasehnejad, M.; Nabiyouni, G.; Gholipour Shahraki, M. Thin film growth by 3D multi-particle diffusion limited aggregation model: Anomalous roughening and fractal analysis. Phys. A Stat. Mech. Its Appl. 2018, 493, 135–147. [Google Scholar] [CrossRef]
- Corwin, I. The Kardar-Parisi-Zhang Equation and Universality Class; World Scientific: Singapore, 2011. [Google Scholar]
- Takeuchi, K.A. An appetizer to modern developments on the Kardar–Parisi–Zhang universality class. Phys. A Stat. Mech. Its Appl. 2018, 504, 77–105. [Google Scholar] [CrossRef]
- Corwin, I. Kardar-Parisi-Zhang Universality. Not. AMS 2016, 63, 230–239. [Google Scholar] [CrossRef]
- Schumacher, O.; Ates, C.; Börnhorst, M.; Koch, R.; Stephan, P. Deposit formation from evaporating urea-water droplets on substrates of different wettability. J. Colloid Interface Sci. 2023, 634, 21. [Google Scholar] [CrossRef] [PubMed]
- Dörnhöfer, J.; Börnhorst, M.; Ates, C.; Samkhaniani, N.; Pfeil, J.; Wörner, M.; Koch, R.; Bauer, H.J.; Deutschmann, O.; Frohnapfel, B.; et al. A Holistic View on Urea Injection for NOx Emission Control: Impingement, Re-atomization, and Deposit Formation. Emiss. Control. Sci. Technol. 2020, 6, 228–243. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ates, C.; Koch, R.; Bauer, H.-J. A Versatile Deposition Model for Natural and Processed Surfaces. Dynamics 2024, 4, 233-253. https://doi.org/10.3390/dynamics4020014
Ates C, Koch R, Bauer H-J. A Versatile Deposition Model for Natural and Processed Surfaces. Dynamics. 2024; 4(2):233-253. https://doi.org/10.3390/dynamics4020014
Chicago/Turabian StyleAtes, Cihan, Rainer Koch, and Hans-Jörg Bauer. 2024. "A Versatile Deposition Model for Natural and Processed Surfaces" Dynamics 4, no. 2: 233-253. https://doi.org/10.3390/dynamics4020014
APA StyleAtes, C., Koch, R., & Bauer, H.-J. (2024). A Versatile Deposition Model for Natural and Processed Surfaces. Dynamics, 4(2), 233-253. https://doi.org/10.3390/dynamics4020014





