Constraining the Inner Galactic DM Density Profile with H.E.S.S.
Abstract
:1. Introduction
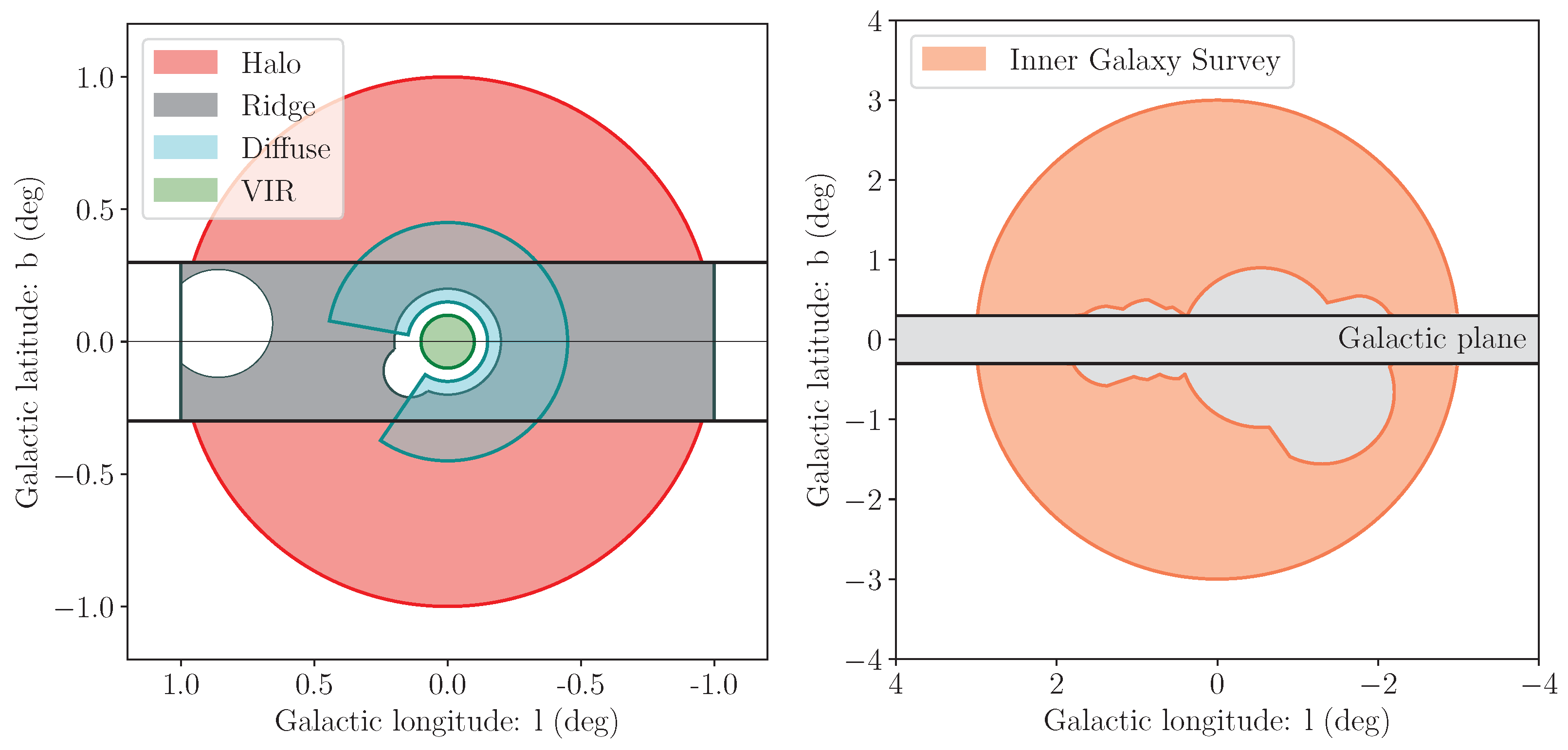
2. The Galactic Center
3. Spectral Modeling
4. Spatial Modeling
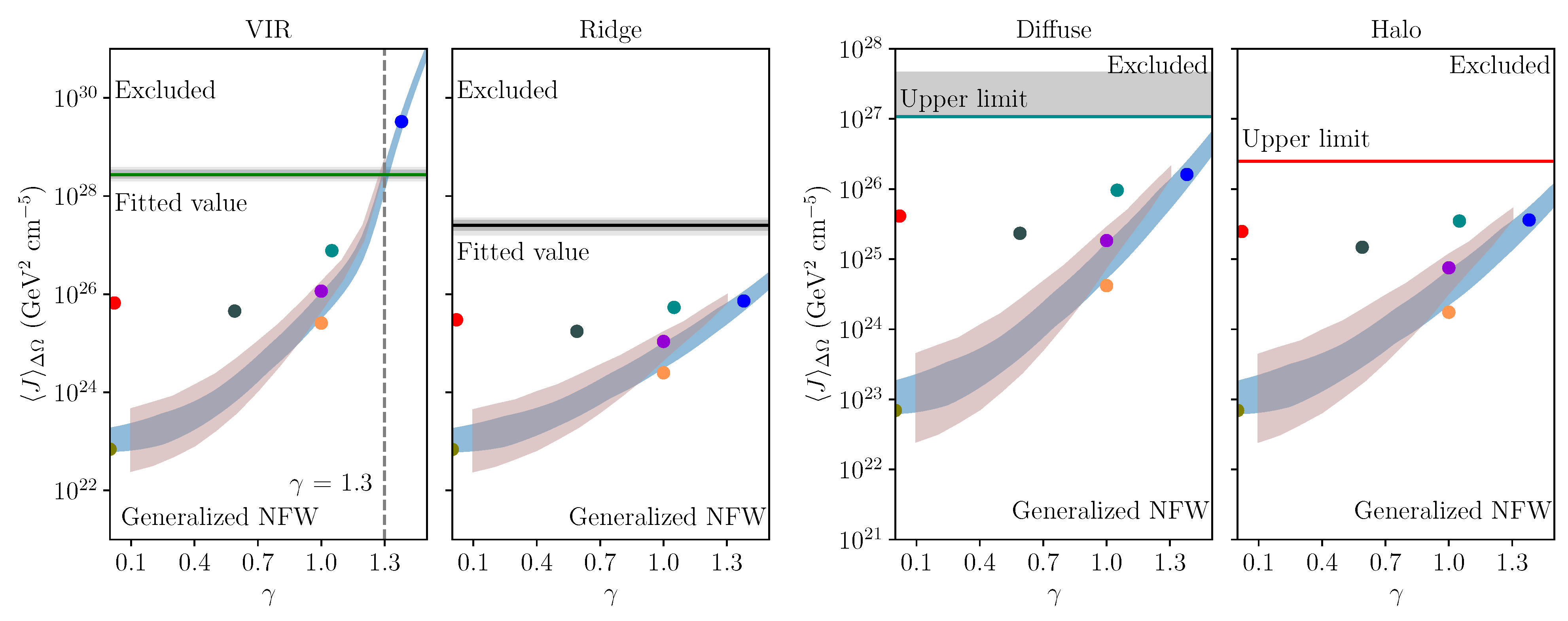
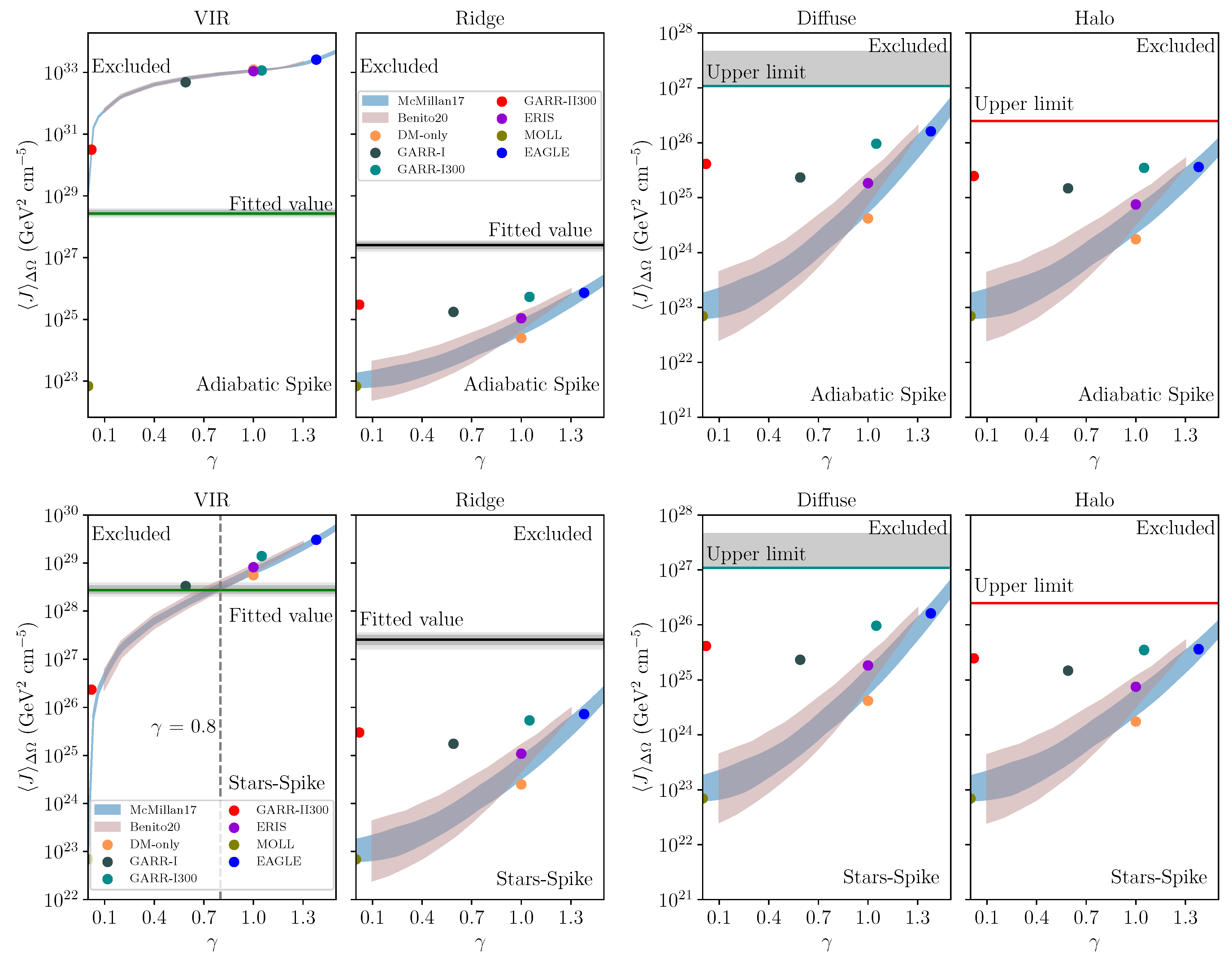
5. Results
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DM | Dark Matter |
| CR | cosmic-ray |
| H.E.S.S. | High Energy Stereoscopic System |
| GC | Galactic Center |
| DRAGON | Diffusion Reacceleration and Advection of Galactic cosmic-rays |
| NFW | Navarro–Frenk–White |
References
- Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6, Erratum in Astron. Astrophys. 2021, 652, C4. [Google Scholar] [CrossRef]
- Benito, M.; Iocco, F.; Cuoco, A. Uncertainties in the Galactic Dark Matter distribution: An update. Phys. Dark Univ. 2021, 32, 100826. [Google Scholar] [CrossRef]
- Clowe, D.; Bradač, M.; Gonzalez, A.H.; Markevitch, M.; Randall, S.W.; Jones, C.; Zaritsky, D. A Direct Empirical Proof of the Existence of Dark Matter. Astrophys. J. 2006, 648, L109–L113. [Google Scholar] [CrossRef]
- Gaskins, J.M. A review of indirect searches for particle dark matter. Contemp. Phys. 2016, 57, 496–525. [Google Scholar] [CrossRef]
- Gammaldi, V. Multimessenger Multi-TeV Dark Matter. Front. Astron. Space Sci. 2019, 6, 19. [Google Scholar] [CrossRef]
- Charles, E.; Sanchez-Conde, M.; Anderson, B.; Caputo, R.; Cuoco, A.; Di Mauro, M.; Drlica-Wagner, A.; Gomez-Vargas, G.A.; Meyer, M.; Tibaldo, L.; et al. Sensitivity Projections for Dark Matter Searches with the Fermi Large Area Telescope. Phys. Rep. 2016, 636, 1–46. [Google Scholar] [CrossRef]
- Delos, M.S.; Korsmeier, M.; Widmark, A.; Blanco, C.; Linden, T.; White, S.D.M. Limits on dark matter annihilation in prompt cusps from the isotropic gamma-ray background. arXiv 2023, arXiv:2307.13023. [Google Scholar]
- Zuriaga-Puig, J.; Gammaldi, V.; Gaggero, D.; Lacroix, T.; Sánchez-Conde, M.A. Multi-TeV dark matter density in the inner Milky Way halo: Spectral and dynamical constraints. J. Cosmol. Astropart. Phys. 2023, 11, 63. [Google Scholar] [CrossRef]
- Cembranos, J.A.R.; Gammaldi, V.; Maroto, A.L. Possible dark matter origin of the gamma ray emission from the Galactic Center observed by HESS. Phys. Rev. D Part. Fields Gravit. Cosmol. 2012, 86, 103506. [Google Scholar] [CrossRef]
- Cembranos, J.A.R.; Gammaldi, V.; Maroto, A.L. Spectral Study of the HESS J1745-290 Gamma-Ray Source as Dark Matter Signal. J. Cosmol. Astropart. Phys. 2013, 4, 51. [Google Scholar] [CrossRef]
- De La Torre Luque, P.; Gaggero, D.; Grasso, D.; Fornieri, O.; Egberts, K.; Steppa, C.; Evoli, C. Galactic diffuse gamma rays meet the PeV frontier. Astron. Astrophys. 2023, 672, A58. [Google Scholar] [CrossRef]
- Abramowski, A.; Aharonian, F.; Benkhali, F.A.; Akhperjanian, A.G.; Angüner, E.O.; Backes, M.; Balzer, A.; Becherini, Y.; Tjus, J.B.; Berge, D.; et al. Acceleration of petaelectronvolt protons in the Galactic Centre. Nature 2016, 531, 476. [Google Scholar] [CrossRef]
- Abdalla, H.; Abramowski, A.; Aharonian, F.; Benkhali, F.A.; Akhperjanian, A.G.; Andersson, T.; Angüner, E.O.; Arakawa, M.; Arrieta, M.; Aubert, P.; et al. Characterising the VHE diffuse emission in the central 200 parsecs of our Galaxy with H.E.S.S. Astron. Astrophys. 2018, 612, A9. [Google Scholar] [CrossRef]
- Abdallah, H.; Abramowski, A.; Aharonian, F.; Benkhali, F.A.; Akhperjanian, A.G.; Angüner, E.; Arrieta, M.; Aubert, P.; Backes, M.; Balzer, A.; et al. Search for dark matter annihilations towards the inner Galactic halo from 10 years of observations with H.E.S.S. Phys. Rev. Lett. 2016, 117, 111301. [Google Scholar] [CrossRef]
- Abramowski, A.; Acero, F.; Aharonian, F.; Akhperjanian, A.G.; Anton, G.; Barnacka, A.; De Almeida, U.B.; Bazer-Bachi, A.R.; Becherini, Y.; Becker, J.; et al. Search for a Dark Matter annihilation signal from the Galactic Center halo with H.E.S.S. Phys. Rev. Lett. 2011, 106, 161301. [Google Scholar] [CrossRef]
- Abdalla, H.; Aharonian, F.; Benkhali, F.A.; Angüner, E.O.; Armand, C.; Ashkar, H.; Backes, M.; Baghmanyan, V.; Martins, V.B.; Batzofin, R.; et al. Search for Dark Matter Annihilation Signals in the H.E.S.S. Inner Galaxy Survey. Phys. Rev. Lett. 2022, 129, 111101. [Google Scholar] [CrossRef] [PubMed]
- Evans, N.W.; Ferrer, F.; Sarkar, S. A travel guide to the dark matter annihilation signal. Phys. Rev. D 2004, 69, 123501. [Google Scholar] [CrossRef]
- Cirelli, M.; Corcella, G.; Hektor, A.; Hütsi, G.; Kadastik, M.; Panci, P.; Raidal, M.; Sala, F.; Strumia, A. PPPC 4 DM ID: A poor particle physicist cookbook for dark matter indirect detection. J. Cosmol. Astropart. Phys. 2011, 3, 51. [Google Scholar] [CrossRef]
- Ciafaloni, P.; Comelli, D.; Riotto, A.; Sala, F.; Strumia, A.; Urbano, A. Weak Corrections are Relevant for Dark Matter Indirect Detection. J. Cosmol. Astropart. Phys. 2011, 3, 19. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Grasso, D.; MacCione, L. Cosmic ray nuclei, antiprotons and gamma rays in the galaxy: A new diffusion model. J. Cosmol. Astropart. Phys. 2008, 10, 018. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Vittino, A.; Bernardo, G.D.; Mauro, M.D.; Ligorini, A.; Ullio, P.; Grasso, D. Cosmic-ray propagation with DRAGON2: I. numerical solver and astrophysical ingredients. J. Cosmol. Astropart. Phys. 2017, 2, 15. [Google Scholar] [CrossRef]
- Gaggero, D.; Grasso, D.; Marinelli, A.; Taoso, M.; Urbano, A. Diffuse cosmic rays shining in the Galactic center: A novel interpretation of H.E.S.S. and Fermi-LAT γ-ray data. Phys. Rev. Lett. 2017, 119, 031101. [Google Scholar] [CrossRef] [PubMed]
- Steigman, G.; Dasgupta, B.; Beacom, J.F. Precise Relic WIMP Abundance and its Impact on Searches for Dark Matter Annihilation. Phys. Rev. D 2012, 86, 023506. [Google Scholar] [CrossRef]
- McMillan, P.J. The mass distribution and gravitational potential of the Milky Way. Mon. Not. R. Astron. Soc. 2017, 465, 76–94. [Google Scholar] [CrossRef]
- Zhao, H. Analytical models for galactic nuclei. Mon. Not. Roy. Astron. Soc. 1996, 278, 488–496. [Google Scholar] [CrossRef]
- Gammaldi, V.; Avila-Reese, V.; Valenzuela, O.; Gonzalez-Morales, A.X. Analysis of the very inner Milky Way dark matter distribution and gamma-ray signals. Phys. Rev. D 2016, 94, 121301. [Google Scholar] [CrossRef]
- Abuter, R.; Aimar, N.; Amorim, A.; Ball, J.; Bauböck, M.; Berger, J.P.; Bonnet, H.; Bourdarot, G.; Brander, W.; Cardoso, V.; et al. Mass distribution in the Galactic Center based on interferometric astrometry of multiple stellar orbits. Astron. Astrophys. 2022, 657, L12. [Google Scholar] [CrossRef]
- Gondolo, P.; Silk, J. Dark matter annihilation at the galactic center. Phys. Rev. Lett. 1999, 83, 1719–1722. [Google Scholar] [CrossRef]
- Sadeghian, L.; Ferrer, F.; Will, C.M. Dark matter distributions around massive black holes: A general relativistic analysis. Phys. Rev. D 2013, 88, 063522. [Google Scholar] [CrossRef]
- Ciucă, I.; Kawata, D.; Ting, Y.S.; Grand, R.J.J.; Miglio, A.; Hayden, M.; Baba, J.; Fragkoudi, F.; Monty, S.; Buder, S.; et al. Chasing the impact of the Gaia-Sausage-Enceladus merger on the formation of the Milky Way thick disc. Mon. Not. R. Astron. Soc. Lett. 2023, 528, L122–L126. [Google Scholar] [CrossRef]
- Vasiliev, E.; Zelnikov, M. Dark matter dynamics in the galactic center. Phys. Rev. D 2008, 78, 083506. [Google Scholar] [CrossRef]
- Bertone, G.; Merritt, D. Dark matter dynamics and indirect detection. Mod. Phys. Lett. A 2005, 20, 1021–1036. [Google Scholar] [CrossRef]
| Profile | ||||||
|---|---|---|---|---|---|---|
| DM-only | 1 | 1 | 3 | |||
| GARR-I | 1 | |||||
| GARR-I300 | 1 | |||||
| GARR-II300 | ||||||
| ERIS | 1 | 1 | 3 | |||
| MOLL | ||||||
| EAGLE | 1 | 3 | ||||
| McMillan17 | 0– | 1 | 3 | – | – | – |
| Benito20 | – | 1 | 3 | – | – | – |
| Parameters | VIR | Ridge | Diffuse | Halo | IGS |
|---|---|---|---|---|---|
| () |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuriaga-Puig, J. Constraining the Inner Galactic DM Density Profile with H.E.S.S. Astronomy 2024, 3, 114-121. https://doi.org/10.3390/astronomy3020008
Zuriaga-Puig J. Constraining the Inner Galactic DM Density Profile with H.E.S.S. Astronomy. 2024; 3(2):114-121. https://doi.org/10.3390/astronomy3020008
Chicago/Turabian StyleZuriaga-Puig, Jaume. 2024. "Constraining the Inner Galactic DM Density Profile with H.E.S.S." Astronomy 3, no. 2: 114-121. https://doi.org/10.3390/astronomy3020008







