Location Optimization of Offline Physical Stores Based on MNL Model under BOPS Omnichannel
Abstract
:1. Introduction
2. Literature Review
2.1. New Retail Model
2.2. Physical Store Location
2.3. Consumer Choice Behavior
2.4. Summary
3. Methods
3.1. Problem Description and Conditional Assumptions
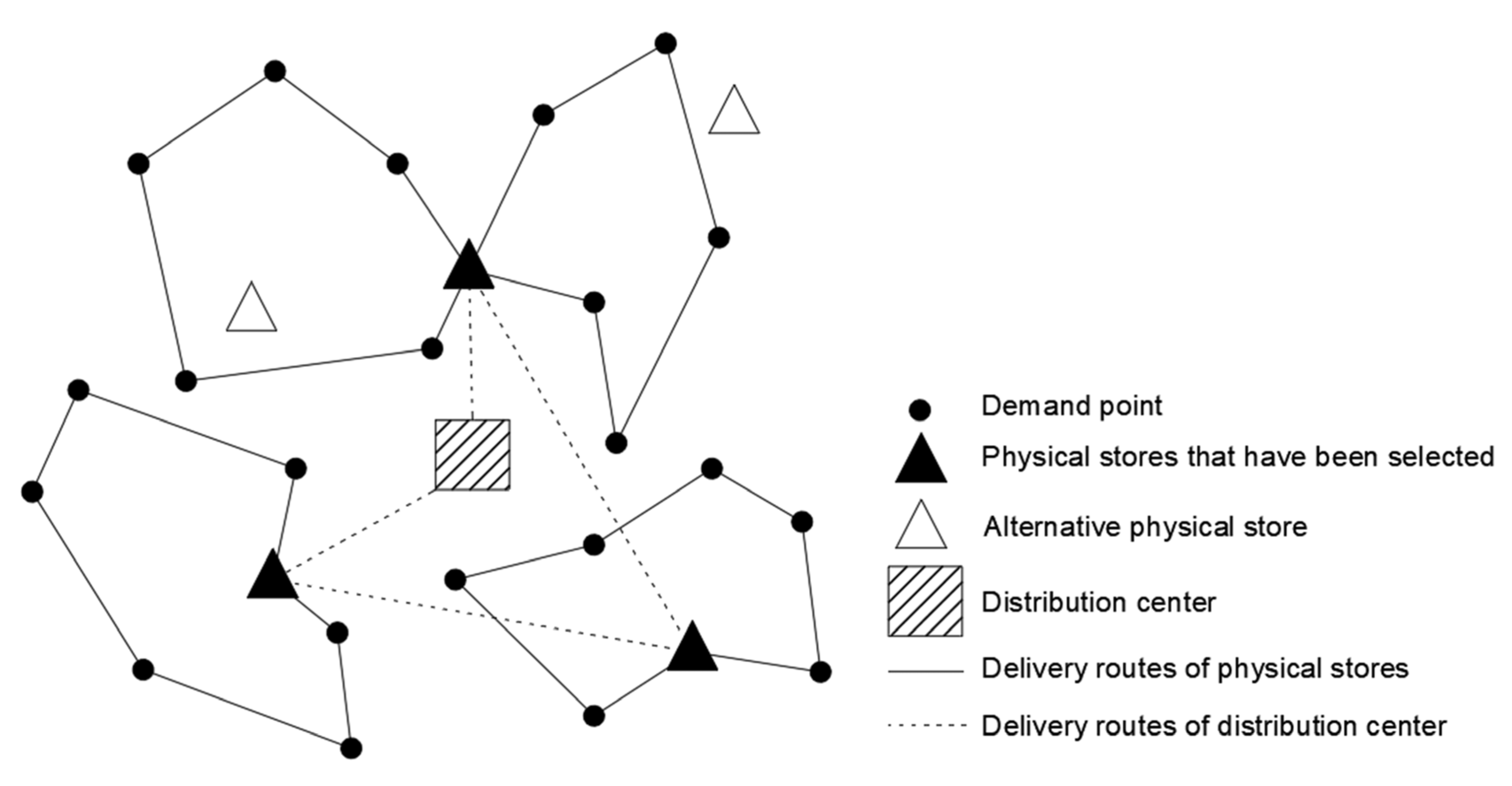
3.1.1. Problem Description
3.1.2. Conditional Assumptions
- (1)
- The total demand of each demand point is known, and only a single product is considered.
- (2)
- The locations of each demand point and alternative physical stores are known.
- (3)
- The number of physical stores required to be built is limited, and the construction cost of physical stores is the same.
- (4)
- Regardless of the inventory level of physical stores, all physical stores balance supply and demand.
- (5)
- The demand of physical stores is met by the distribution center. Customers’ demands in the physical channel, online channel, and BOPS channel are met by physical stores.
- (6)
- The online channel needs of customers in each demand point can only be met by one physical store. One physical store can meet the online channel needs of customers in multiple demand points, and goods cannot be transferred between physical stores.
- (7)
- From the distribution center to the physical store and from the physical store to the demand point, two kinds of vehicles with different load capacities are used for distribution. The number of vehicles owned by the enterprise is known.
- (8)
- The delivery vehicle must return to the original place of departure after completing the delivery task. The traffic speed is constant, and the road is clear.
- (9)
- There is no product shortage problem in any channel.
3.2. Characterization of Customer Choice Behavior
3.2.1. Utility Function
- (1)
- Online channel utility function
- (2)
- BOPS channel utility function
- (3)
- Offline physical channel utility function
3.2.2. Customer Channel Choice Behavior
3.3. Model Construction
3.3.1. Construction Cost of Offline Physical Stores
3.3.2. Vehicle Transportation Cost
3.3.3. Penalty Cost of Return
3.3.4. Objective Function
3.4. Design of Improved Genetic Algorithm
3.4.1. Chromosome Coding and Initial Population Formation
3.4.2. Calculation of Individual Fitness
3.4.3. Selection
3.4.4. Crossover
3.4.5. Variation
3.4.6. Algorithm Termination
4. Example Results and Discussion
4.1. Example Verification
4.2. Sensitivity Analysis
4.2.1. The Effect of Freight on Total Enterprise Cost and Customer Choice Behavior
4.2.2. The Effect of Return Rate on Total Enterprise Cost and Customer Choice Behavior
4.2.3. The Effect of the Service Level of Physical Stores on Total Enterprise Cost and Customer Choice Behavior
4.3. Algorithm Validity Analysis
5. Conclusions
- (1)
- Enterprises should pay more attention to freight level and enhance offline business capabilities
- (2)
- Enterprises should take measures to reduce return rate
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Difrancesco, R.M.; van Schilt, I.M.; Winkenbach, M. Optimal in-store fulfillment policies for online orders in an omni-channel retail environment. Eur. J. Oper. Res. 2021, 293, 1058–1076. [Google Scholar] [CrossRef]
- Song, Y.; Fan, T.; Tang, Y.; Xu, C. Omni-channel strategies for fresh produce with extra losses in-store. Transp. Res. Part E Logist. Transp. Rev. 2021, 148, 102243. [Google Scholar] [CrossRef]
- Saha, K.; Bhattacharya, S. ‘Buy online and pick up in-store’: Implications for the store inventor. Eur. J. Oper. Res. 2021, 294, 906–921. [Google Scholar] [CrossRef]
- Zhang, A.; Ren, J.; Guan, Z.; Farooq, U. Decision and Coordination in the Dual-Channel Supply Chain Considering the Risk-Averse and Customer Returns. J. Math. Financ. 2021, 11, 48–83. [Google Scholar] [CrossRef]
- Esmaeili, N.; Teimoury, E.; Pourmohammadi, F. A scenario-based optimization model for planning and redesigning the sale and after-sales services closed-loop supply chain. RAIRO-Oper. Res. 2021, 55, S2859–S2877. [Google Scholar] [CrossRef]
- Pangarkar, A.; Arora, V.; Shukla, Y. Exploring phygital omnichannel luxury retailing for immersive customer experience: The role of rapport and social engagement. J. Retail. Consum. Serv. 2022, 68, 103001. [Google Scholar] [CrossRef]
- Momen, S.; Torabi, S.A. Omni-channel retailing: A data-driven distributionally robust approach for integrated fulfillment services under competition with traditional and online retailers. Comput. Ind. Eng. 2021, 157, 107353. [Google Scholar] [CrossRef]
- Adivar, B.; Hüseyinoğlu, I.Y.; Christopher, M. A quantitative performance management framework for assessing omnichannel retail supply chains. J. Retail. Consum. Serv. 2019, 48, 257–269. [Google Scholar] [CrossRef]
- Gallino, S.; Moreno, A. Integration of Online and Offline Channels in Retail: The Impact of Sharing Reliable Inventory Availability Information. Manag. Sci. 2014, 60, 1434–1451. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Shi, X. Solving the location problem of front distribution center for omni-channel retailing. Complex Intell. Syst. 2021, in press. [CrossRef]
- Xu, N.; Huang, Y.-F.; Weng, M.-W.; Do, M.-H. New Retailing Problem for an Integrated Food Supply Chain in the Baking Industry. Appl. Sci. 2021, 11, 946. [Google Scholar] [CrossRef]
- Gao, F.; Su, X. Omnichannel Retail Operations with Buy-Online-and-Pick-up-in-Store. Manag. Sci. 2017, 63, 2478–2492. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Tian, L.; Wang, C.; Wang, S. Optimal service decisions in an omni-channel with buy-online-and-pick-up-in-store. J. Oper. Res. Soc. 2020, 73, 794–810. [Google Scholar] [CrossRef]
- Radhi, M.; Zhang, G. Optimal cross-channel return policy in dual-channel retailing systems. Int. J. Prod. Econ. 2019, 210, 184–198. [Google Scholar] [CrossRef]
- Pichka, K.; Alwan, L.C.; Yue, X. Fulfillment and pricing optimization for omni-channel retailers considering shipment of in-store demand. Transp. Res. Part E Logist. Transp. Rev. 2022, 167, 102912. [Google Scholar] [CrossRef]
- Paul, J.; Agatz, N.; Savelsbergh, M. Optimizing Omni-Channel Fulfillment with Store Transfers. Transp. Res. Part B Methodol. 2019, 129, 381–396. [Google Scholar] [CrossRef]
- Bayram, A.; Cesaret, B. Order Fulfillment Policies for Ship-from-Store Implementation in Omni-Channel Retailing. Eur. J. Oper. Res. 2020, 294, 987–1002. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Y.; Liu, W.; Ma, Y.; Xiang, L.; Yang, Y.; Li, X. How to achieve a win–win scenario between cost and customer satisfaction for cold chain logistics? Phys. A Stat. Mech. Its Appl. 2021, 566, 125637. [Google Scholar] [CrossRef]
- Wang, Y.; Assogba, K.; Liu, Y.; Ma, X.; Xu, M.; Wang, Y. Two-echelon location-routing optimization with time windows based on customer clustering. Expert Syst. Appl. 2018, 104, 244–260. [Google Scholar] [CrossRef]
- Dou, S.; Liu, G.; Yang, Y. A New Hybrid Algorithm for Cold Chain Logistics Distribution Center Location Problem. IEEE Access 2020, 8, 88769–88776. [Google Scholar] [CrossRef]
- Zhang, S.; Chen, N.; She, N.; Li, K. Location optimization of a competitive distribution center for urban cold chain logistics in terms of low-carbon emissions. Comput. Ind. Eng. 2021, 154, 107120. [Google Scholar] [CrossRef]
- Li, X.; Zhou, K. Multi-objective cold chain logistic distribution center location based on carbon emission. Environ. Sci. Pollut. Res. 2021, 28, 32396–32404. [Google Scholar] [CrossRef] [PubMed]
- Alamatsaz, K.; Ahmadi, A.; Al-E-Hashem, S.M.J.M. A multiobjective model for the green capacitated location-routing problem considering drivers’ satisfaction and time window with uncertain demand. Environ. Sci. Pollut. Res. 2022, 29, 5052–5071. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, J.; Fan, H.; Wang, L.; Yang, M.; Ma, Y. Site Selection Improvement of Retailers Based on Spatial Competition Strategy and a Double-Channel Convolutional Neural Network. ISPRS Int. J. Geo-Inf. 2020, 9, 357. [Google Scholar] [CrossRef]
- Agrebi, M.; Abed, M. Decision-making from multiple uncertain experts: Case of distribution center location selection. Soft Comput. 2021, 25, 4525–4544. [Google Scholar] [CrossRef]
- Fathi, M.; Khakifirooz, M.; Diabat, A.; Chen, H. An integrated queuing-stochastic optimization hybrid Genetic Algorithm for a location-inventory supply chain network. Int. J. Prod. Econ. 2021, 237, 108139. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, Z.; Ji, Y.; Qu, S.; Raza, H. Two-stage distributionally robust mixed-integer optimization model for three-level location-allocation problems under uncertain environment. Phys. A Stat. Mech. Its Appl. 2021, 572, 125872. [Google Scholar] [CrossRef]
- Marianov, V.; Eiselt, H.; Lüer-Villagra, A. Effects of multipurpose shopping trips on retail store location in a duopoly. Eur. J. Oper. Res. 2018, 269, 782–792. [Google Scholar] [CrossRef]
- Zhang, H.; Feng, H.; Wang, H. Two-Stage Optimization Model of Agricultural Product Distribution in Remote Rural Areas. IEEE Access 2020, 8, 213928–213949. [Google Scholar] [CrossRef]
- Yu, V.F.; Jodiawan, P.; Hou, M.-L.; Gunawan, A. Design of a two-echelon freight distribution system in last-mile logistics considering covering locations and occasional drivers. Transp. Res. Part E Logist. Transp. Rev. 2021, 154, 102461. [Google Scholar] [CrossRef]
- Yang, J.; Guo, F.; Zhang, M. Optimal planning of swapping/charging station network with customer satisfaction. Transp. Res. Part E Logist. Transp. Rev. 2017, 103, 174–197. [Google Scholar] [CrossRef]
- Xu, X.; Jackson, J.E. Investigating the Influential Factors of Return Channel Loyalty in Omni-Channel Retailing. Int. J. Prod. Econ. 2019, 216, 118–132. [Google Scholar] [CrossRef]
- Marianov, V.; Ríos, M.; Icaza, M.J. Facility location for market capture when users rank facilities by shorter travel and waiting times. Eur. J. Oper. Res. 2007, 191, 32–44. [Google Scholar] [CrossRef]
- Zhang, Y.; Berman, O.; Verter, V. The impact of client choice on preventive healthcare facility network design. OR Spectr. 2012, 34, 349–370. [Google Scholar] [CrossRef]
- Haase, K.; Müller, S. Insights into clients’ choice in preventive health care facility location planning. OR Spectr. 2015, 37, 273–291. [Google Scholar] [CrossRef]
- Al-Salih, W.; Esztergár-Kiss, D. Linking Mode Choice with Travel Behavior by Using Logit Model Based on Utility Function. Sustainability 2021, 13, 4332. [Google Scholar] [CrossRef]
- Kucukyazici, B.; Zhang, Y.; Ardestani-Jaafari, A.; Song, L. Incorporating Patient Preferences in the Design and Operation of Cancer Screening Facility Networks. Eur. J. Oper. Res. 2020, 287, 616–632. [Google Scholar] [CrossRef]
- Krohn, R.; Müller, S.; Haase, K. Preventive healthcare facility location planning with quality-conscious clients. OR Spectr. 2021, 43, 59–87. [Google Scholar] [CrossRef]
- Haase, K.; Müller, S. A comparison of linear reformulations for multinomial logit choice probabilities in facility location models. Eur. J. Oper. Res. 2014, 232, 689–691. [Google Scholar] [CrossRef]
- Chen, Y.; Han, P.; Zeng, Q. Multi-objective location problem of pick-up point considering the impact of home delivery. Comput. Integr. Manuf. Syst. 2016, 22, 2679–2690. (In Chinese) [Google Scholar] [CrossRef]
- Chen, G.; Fu, J.; He, M. Emergency Shelter Location Problem Considering Residents’ Choice Behavior. Oper. Res. Manag. Sci. 2019, 28, 6–14. (In Chinese) [Google Scholar] [CrossRef]






| Literature | Primary Focus | Customer Behavior | Behavior Description Mode | Solution Approach |
|---|---|---|---|---|
| Marianov et al. [33], (2007) | Preventive facility congestion | Yes | MNL | Heuristic |
| Haase and Muller [35], (2015) | Customer participation in preventive facilities | Yes | MNL | Optimization Package |
| Yang et al. [31], (2017) | Customer satisfaction related to range anxiety and loss anxiety | Yes | Linear elastic formula | Heuristic; Simulation |
| Wang et al. [19], (2018) | Time window and customer clustering | No | No | Heuristic |
| Marianov et al. [28], (2018) | Customers’ purchase of multiple commodities | No | No | Heuristic; Simulation |
| Zhang et al. [29], (2020) | Clustering between logistics nodes | No | No | Heuristic |
| Dou et al. [20], (2020) | Freshness and time window | No | No | Heuristic |
| Ouyang et al. [24], (2020) | Differences in the spatial distribution of the factors of site selection | No | No | Linear Regression; Simulation |
| Kucukyazici et al. [37], (2020) | Heterogeneity of patients | Yes | M/G/s; MNL | Heuristic; Simulation |
| Agrebi and Abed [25], (2021) | Inherent uncertainty and imprecision of decision making, market. | No | No | Simulation |
| Zhang et al. [21], (2021) | Carbon emission | No | No | Heuristic |
| Krohn et al. [38], (2021) | Waiting time and care quality of cancer detection facility | Yes | MNL | GAMS; CPLEX |
| Li et al. [22], (2021) | Carbon emission | No | No | Heuristic |
| Huang et al. [10], (2021) | Facility’s capacity, demand, and rent fluctuation | No | No | Heuristic; Simulation |
| Liu et al. [27], (2021) | Uncertain transportation cost and customer demand | No | No | Heuristic |
| Wang et al. [18], (2021) | Time requirements of customers | No | No | Heuristic |
| Fathi et al. [26], (2021) | Customer demand and inventory strategy | No | No | Queuing Theory; Heuristic |
| Yu et al. [30], (2021) | Covering locations and occasional drivers | No | No | Heuristic |
| Alamatsaz et al. [23], (2022) | Driver satisfaction and time window | No | No | Heuristic |
| This paper | Customer choice behavior | Yes | MNL | Heuristic |
| Parameters | Definition |
|---|---|
| The collection of demand points | |
| The collection of alternative locations for physical stores | |
| The collection of small delivery vehicles from physical stores to demand points | |
| The collection of large delivery vehicles from distribution centers to physical stores | |
| The collection of distribution centers | |
| The collection of nodes through which vehicle travels from physical store to demand point , , | |
| The collection of nodes through which vehicle travels from distribution center to physical store , , | |
| Quantity demanded at demand point | |
| The freight borne by customers when purchasing products in the online channel | |
| The average return rate of customers at demand point when they purchase products in the online channel | |
| The distance from the customer at demand point to the physical store to pick up or purchase products | |
| Customer’s distance sensitivity coefficient | |
| The service level of physical stores | |
| The average shopping time of customers at demand point in physical stores | |
| The construction cost of physical store | |
| The carrying capacity of a small vehicle | |
| The carrying capacity of a large vehicle | |
| The unit distribution cost of a small vehicle | |
| The unit distribution cost of a large vehicle | |
| The distance from demand point to physical store | |
| The distance traveled by vehicle from physical store to demand point | |
| The distance traveled by vehicle from distribution center to physical store | |
| Quantity purchased by customers in the online channel and distributed by physical store | |
| Quantity purchased by customers in the BOPS channel and picked up in physical store | |
| Quantity purchased by customers in physical store | |
| The total quantity demanded by physical store | |
| The unit penalty cost of unmet customer demand at demand point | |
| Binary variable equal to 1 if alternative site is selected to build a physical store and 0 otherwise, | |
| Binary variable equal to 1 if the online demand of demand point is delivered by physical store and 0 otherwise, | |
| Binary variable equal to 1 if vehicle travels from point to point and 0 otherwise, | |
| Binary variable equal to 1 if vehicle travels from point to point and 0 otherwise, |
| Gene Segment | A | B | C | D | E |
|---|---|---|---|---|---|
| Coding digit | digit | digit | digit | digit | digit |
| Coding content | Small delivery vehicle number | Demand point number | Alternate physical store number | Large delivery vehicle number | Alternate physical store number |
| Number | Coordinates | Quantity Demanded | Number | Coordinates | Quantity Demanded |
|---|---|---|---|---|---|
| 1 | (80.14, 4.41) | 90.74 | 16 | (89.60, 40.89) | 57.09 |
| 2 | (34.65, 68.67) | 60.29 | 17 | (42.05, 89.96) | 71.09 |
| 3 | (8.33, 73.38) | 56.35 | 18 | (54.45, 14.36) | 95.79 |
| 4 | (51.11, 63.72) | 65.67 | 19 | (60.64, 87.13) | 89.61 |
| 5 | (36.68, 37.98) | 81.62 | 20 | (21.56, 86.04) | 77.97 |
| 6 | (73.95, 97.97) | 54.88 | 21 | (76.04, 8.32) | 82.79 |
| 7 | (92.06, 9.86) | 63.92 | 22 | (29.96, 72.04) | 51.79 |
| 8 | (80.45, 44.02) | 77.34 | 23 | (38.29, 3.04) | 92.46 |
| 9 | (15.04, 10.03) | 69.88 | 24 | (8.46, 85.32) | 96.70 |
| 10 | (18.95, 32.60) | 78.24 | 25 | (51.64, 91.03) | 53.94 |
| 11 | (12.37, 31.41) | 57.88 | 26 | (33.20, 21.45) | 74.89 |
| 12 | (82.10, 89.45) | 66.53 | 27 | (83.97, 67.99) | 87.16 |
| 13 | (63.79, 24.7) | 71.86 | 28 | (38.96, 84.10) | 69.61 |
| 14 | (21.02, 65.43) | 74.27 | 29 | (82.82, 85.07) | 82.77 |
| 15 | (1.61, 31.07) | 90.01 | 30 | (17.65, 55.86) | 58.56 |
| Number | Coordinates | Number | Coordinates |
|---|---|---|---|
| 1 | (40.50, 92.92) | 6 | (48.99, 27.28) |
| 2 | (17.36, 48.99) | 7 | (10.66, 79.86) |
| 3 | (57.52, 69.49) | 8 | (87.26, 10.87) |
| 4 | (60.62, 41.14) | 9 | (71.55, 59.83) |
| 5 | (21.44, 13.48) | 10 | (90.12, 86.55) |
| Number | Coordinates |
|---|---|
| 1 | (35.81, 48.90) |
| Vehicle | Distribution Route |
|---|---|
| small vehicle 1 | no. 9 physical store→27→30→14→no. 9 physical store |
| small vehicle 2 | no. 9 physical store→4→3→1→23→no. 9 physical store |
| small vehicle 3 | no. 7 physical store→25→5→13→18→11→26→no. 7 physical store |
| small vehicle 4 | no. 8 physical store→8→10→19→6→17→no. 8 physical store |
| small vehicle 5 | no. 2 physical store→24→28→12→29→16→21→22→7→9→no. 2 physical store |
| small vehicle 6 | no. 2 physical store→15→20→2→no. 2 physical store |
| large vehicle 1 | distribution center→no. 2 physical store→no. 7 physical store→distribution center |
| large vehicle 2 | distribution center→no. 8 physical store→no. 9 physical store→distribution center |
| Number | Number | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 0.24 | 0.43 | 0.34 | 16 | 0.28 | 0.33 | 0.38 |
| 2 | 0.29 | 0.35 | 0.36 | 17 | 0.29 | 0.30 | 0.41 |
| 3 | 0.24 | 0.42 | 0.33 | 18 | 0.28 | 0.29 | 0.42 |
| 4 | 0.28 | 0.39 | 0.33 | 19 | 0.27 | 0.30 | 0.43 |
| 5 | 0.31 | 0.26 | 0.43 | 20 | 0.23 | 0.40 | 0.37 |
| 6 | 0.31 | 0.28 | 0.41 | 21 | 0.21 | 0.36 | 0.43 |
| 7 | 0.23 | 0.40 | 0.37 | 22 | 0.25 | 0.33 | 0.42 |
| 8 | 0.22 | 0.33 | 0.45 | 23 | 0.36 | 0.31 | 0.33 |
| 9 | 0.37 | 0.32 | 0.32 | 24 | 0.23 | 0.43 | 0.34 |
| 10 | 0.34 | 0.29 | 0.37 | 25 | 0.32 | 0.30 | 0.38 |
| 11 | 0.35 | 0.29 | 0.36 | 26 | 0.30 | 0.26 | 0.43 |
| 12 | 0.27 | 0.29 | 0.43 | 27 | 0.24 | 0.39 | 0.37 |
| 13 | 0.25 | 0.30 | 0.44 | 28 | 0.28 | 0.32 | 0.40 |
| 14 | 0.26 | 0.39 | 0.35 | 29 | 0.30 | 0.35 | 0.35 |
| 15 | 0.33 | 0.29 | 0.38 | 30 | 0.26 | 0.31 | 0.43 |
| Algorithm | Optimal Solution/(CNY 10,000) | Average Total Cost/(CNY 10,000) | Standard Deviation of Total Cost | Average Running Time/(s) |
|---|---|---|---|---|
| Traditional genetic algorithm | 137.43 | 146.78 | 6.06 | 269.70 |
| Improved genetic algorithm | 129.53 | 134.45 | 2.81 | 235.10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, P.; Zhang, J.; Liu, Y.; Jiang, X. Location Optimization of Offline Physical Stores Based on MNL Model under BOPS Omnichannel. J. Theor. Appl. Electron. Commer. Res. 2022, 17, 1633-1654. https://doi.org/10.3390/jtaer17040083
Wan P, Zhang J, Liu Y, Jiang X. Location Optimization of Offline Physical Stores Based on MNL Model under BOPS Omnichannel. Journal of Theoretical and Applied Electronic Commerce Research. 2022; 17(4):1633-1654. https://doi.org/10.3390/jtaer17040083
Chicago/Turabian StyleWan, Peng, Jie Zhang, Yiwei Liu, and Xiaoxuan Jiang. 2022. "Location Optimization of Offline Physical Stores Based on MNL Model under BOPS Omnichannel" Journal of Theoretical and Applied Electronic Commerce Research 17, no. 4: 1633-1654. https://doi.org/10.3390/jtaer17040083







