Entrained-Flow Coal Gasification Process Simulation with the Emphasis on Empirical Char Conversion Models Optimization Procedure
Abstract
:1. Introduction
2. Numerical Models
2.1. CFD Modeling of Entrained-Flow Gasification
2.1.1. Devolatilization Modeling
2.1.2. Char Conversion Modeling
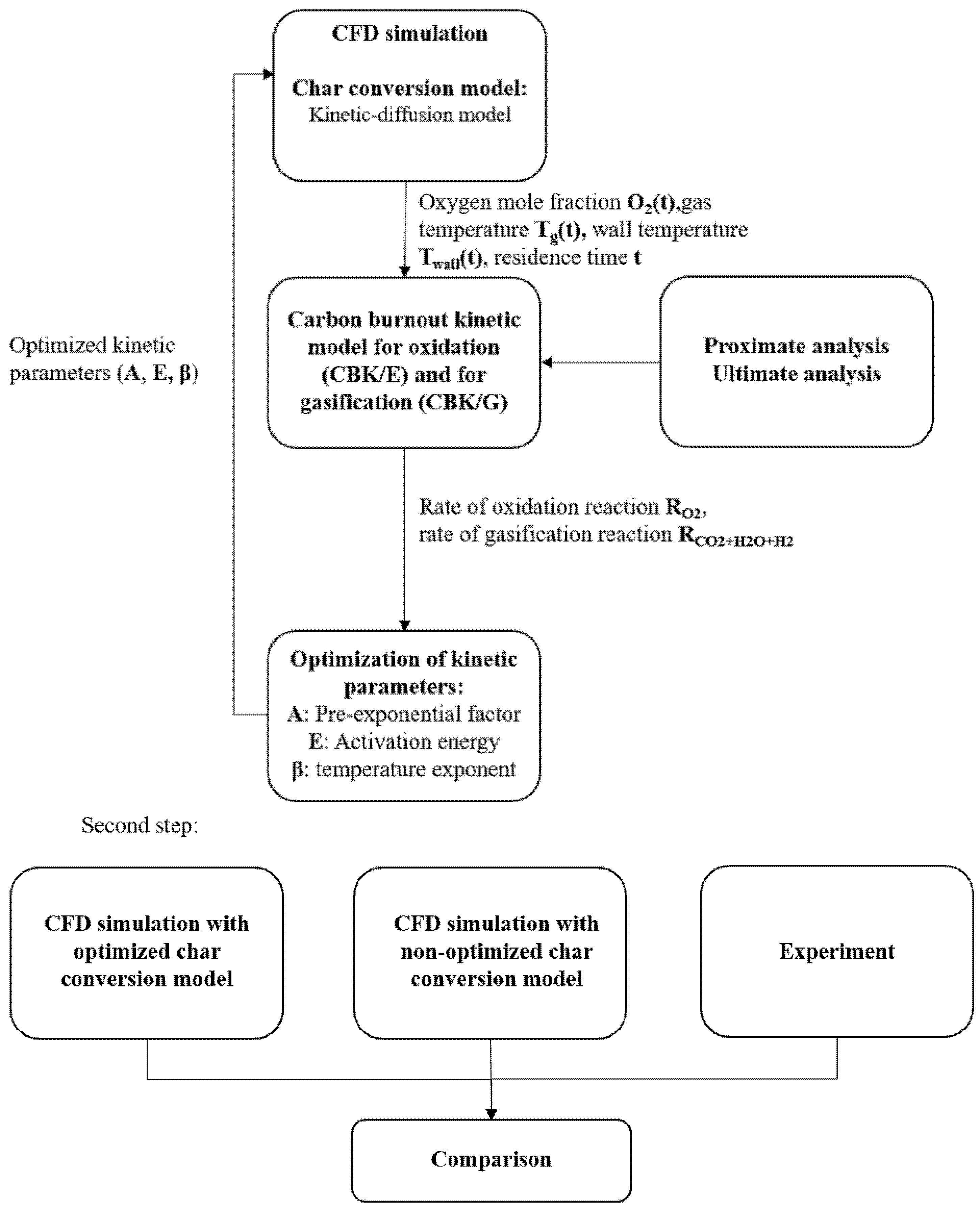
3. Optimization Procedure
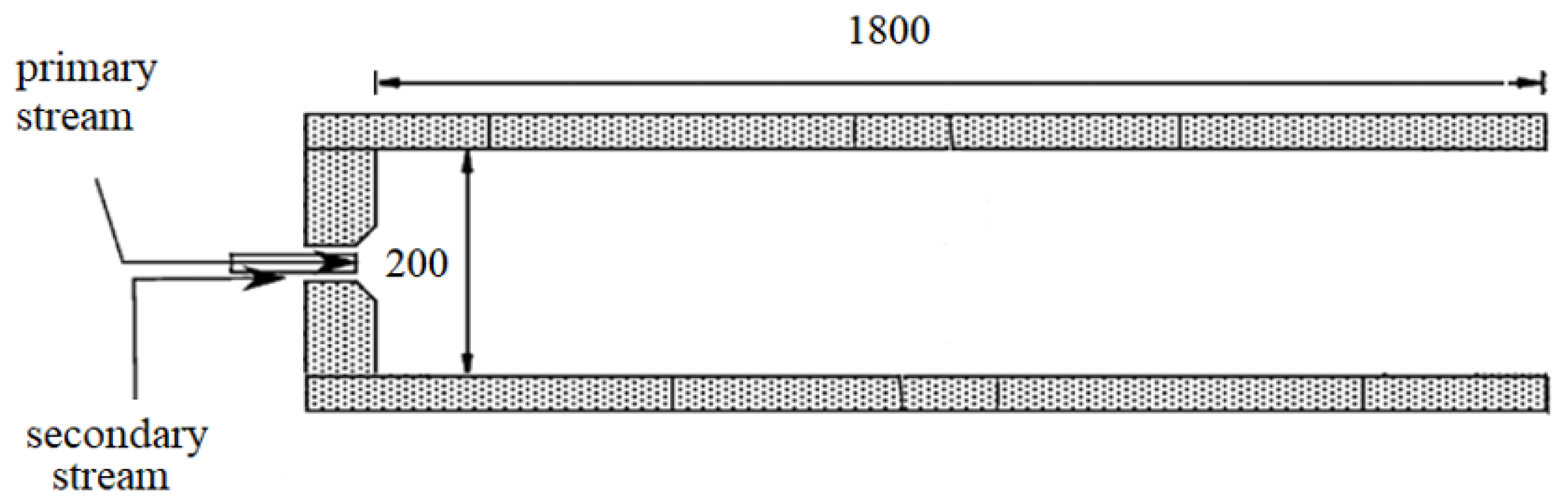
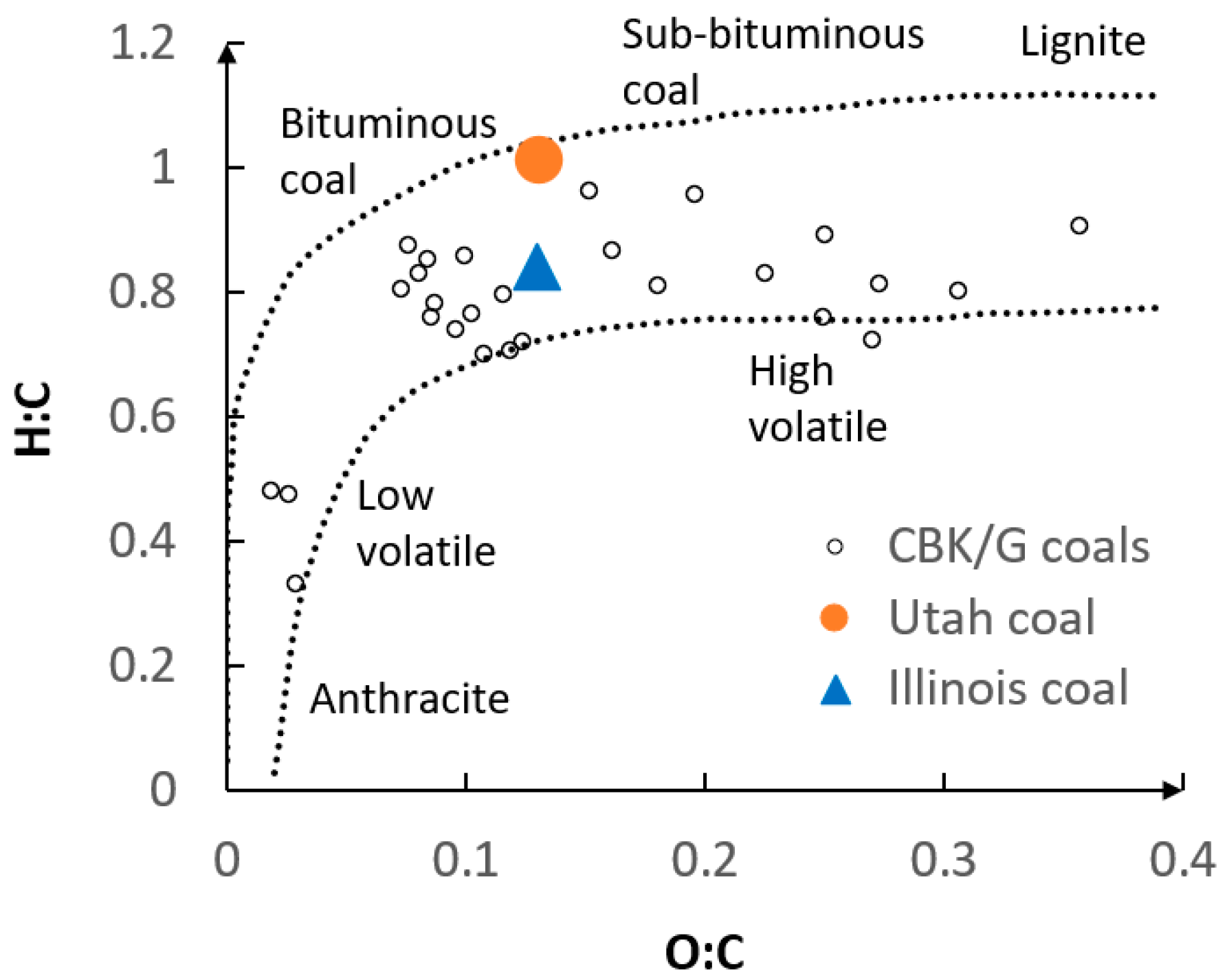
4. Reactor. Computational Domain
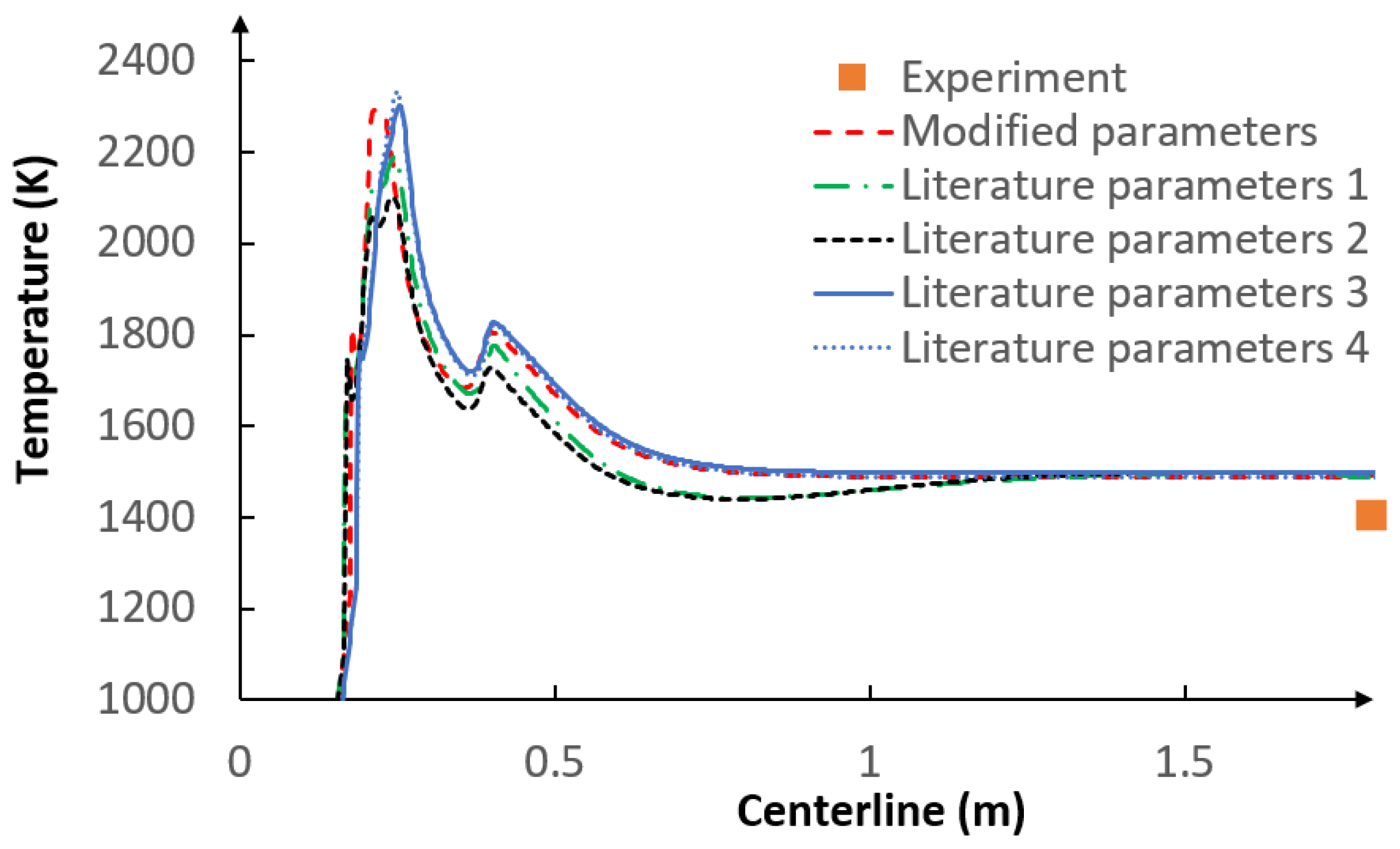
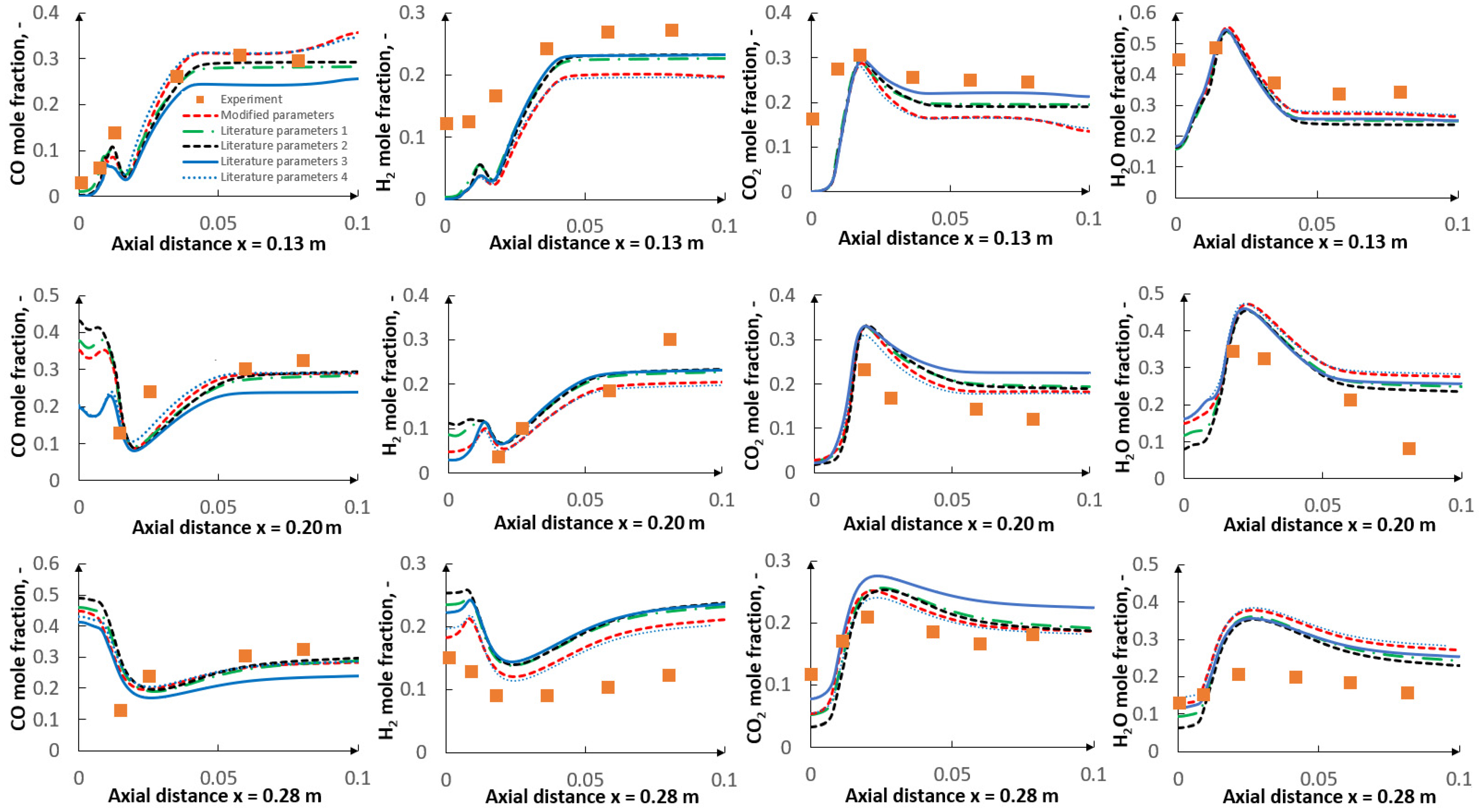
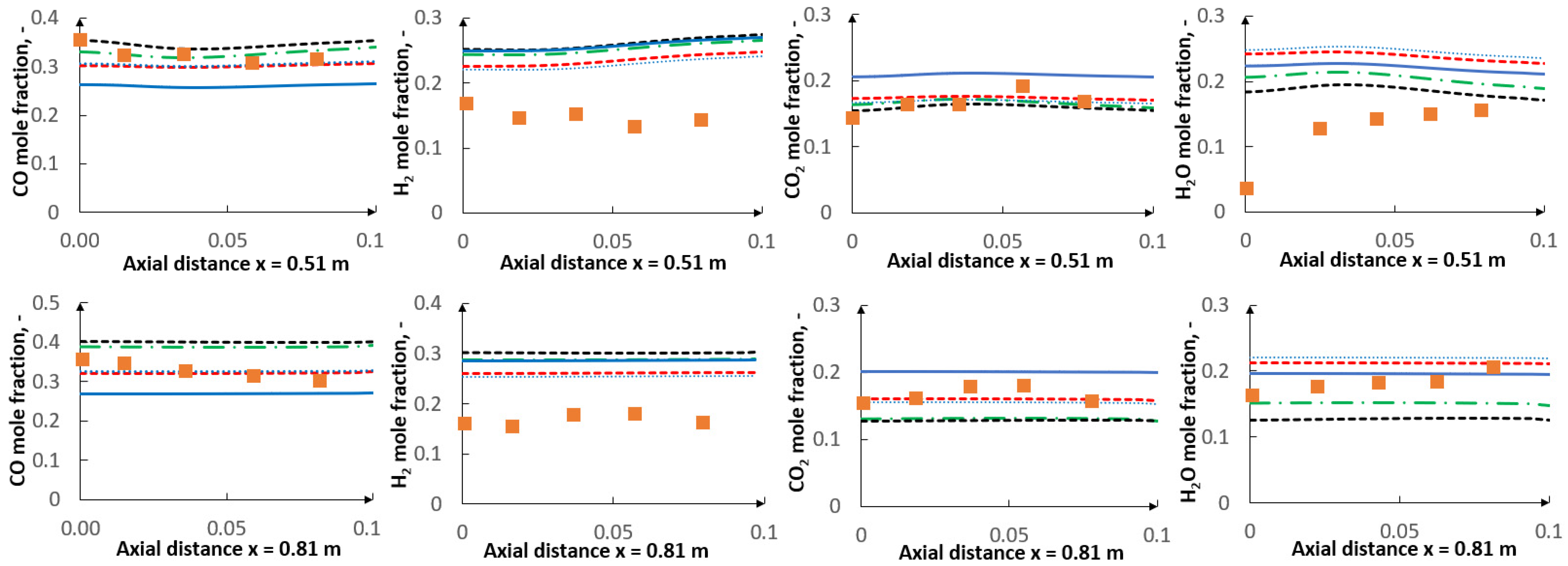
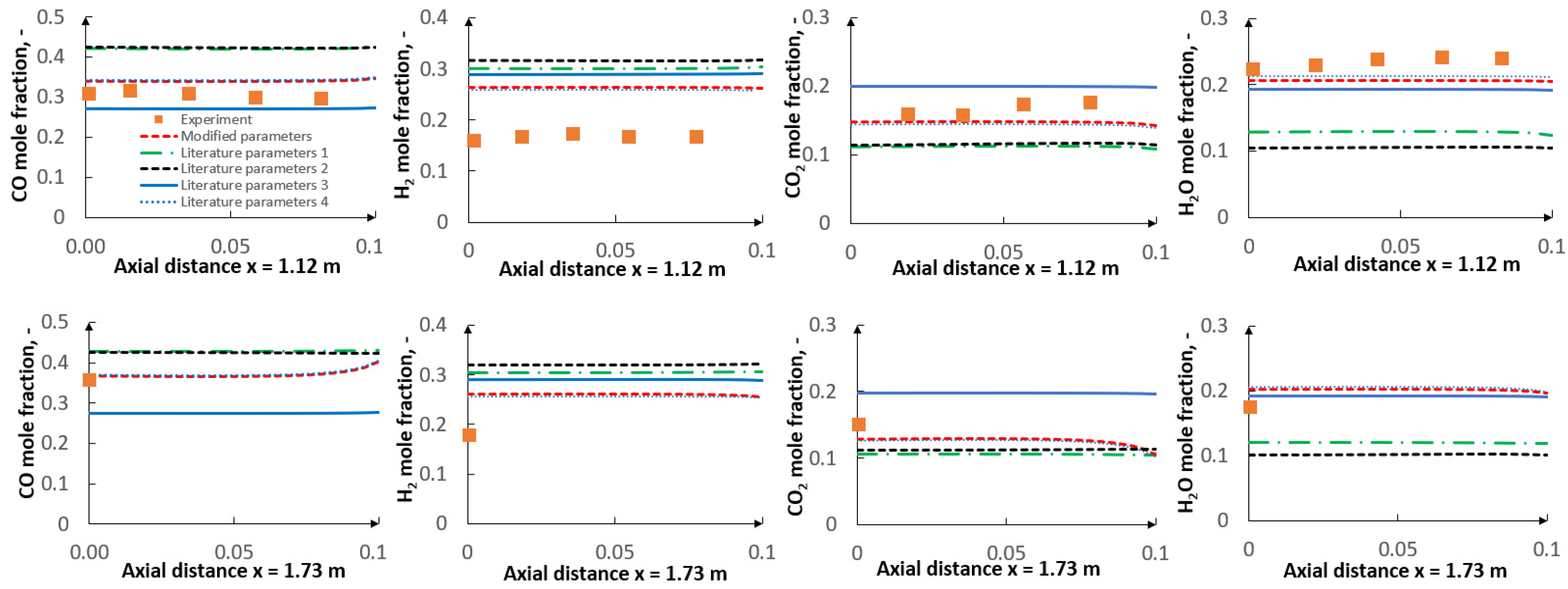
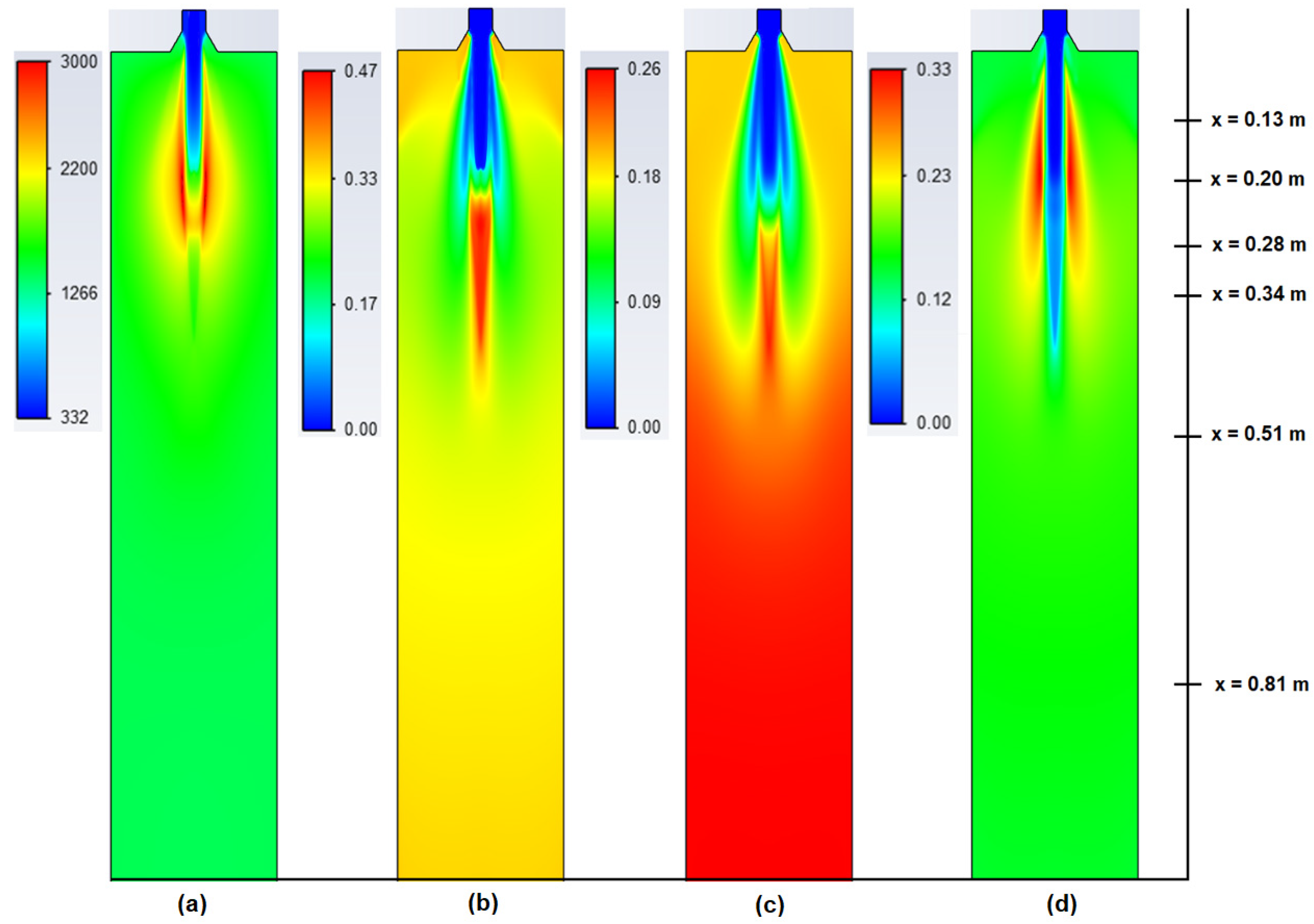
5. Results
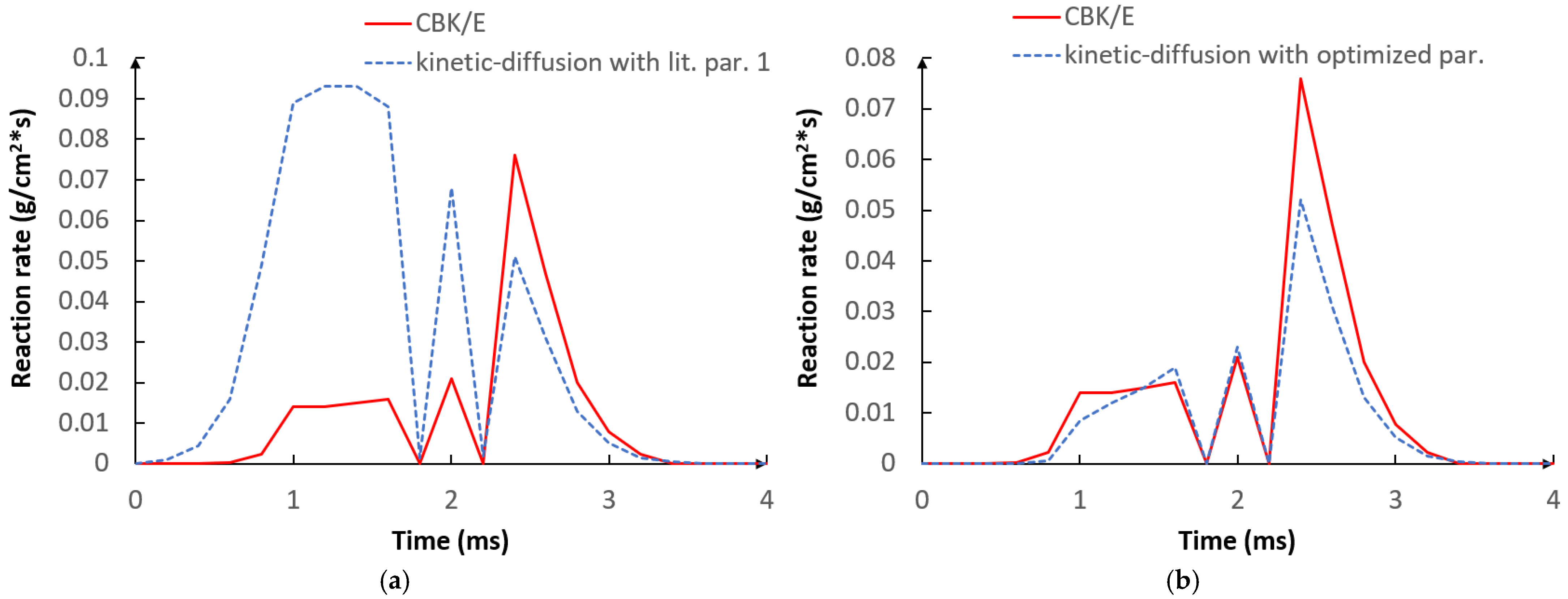
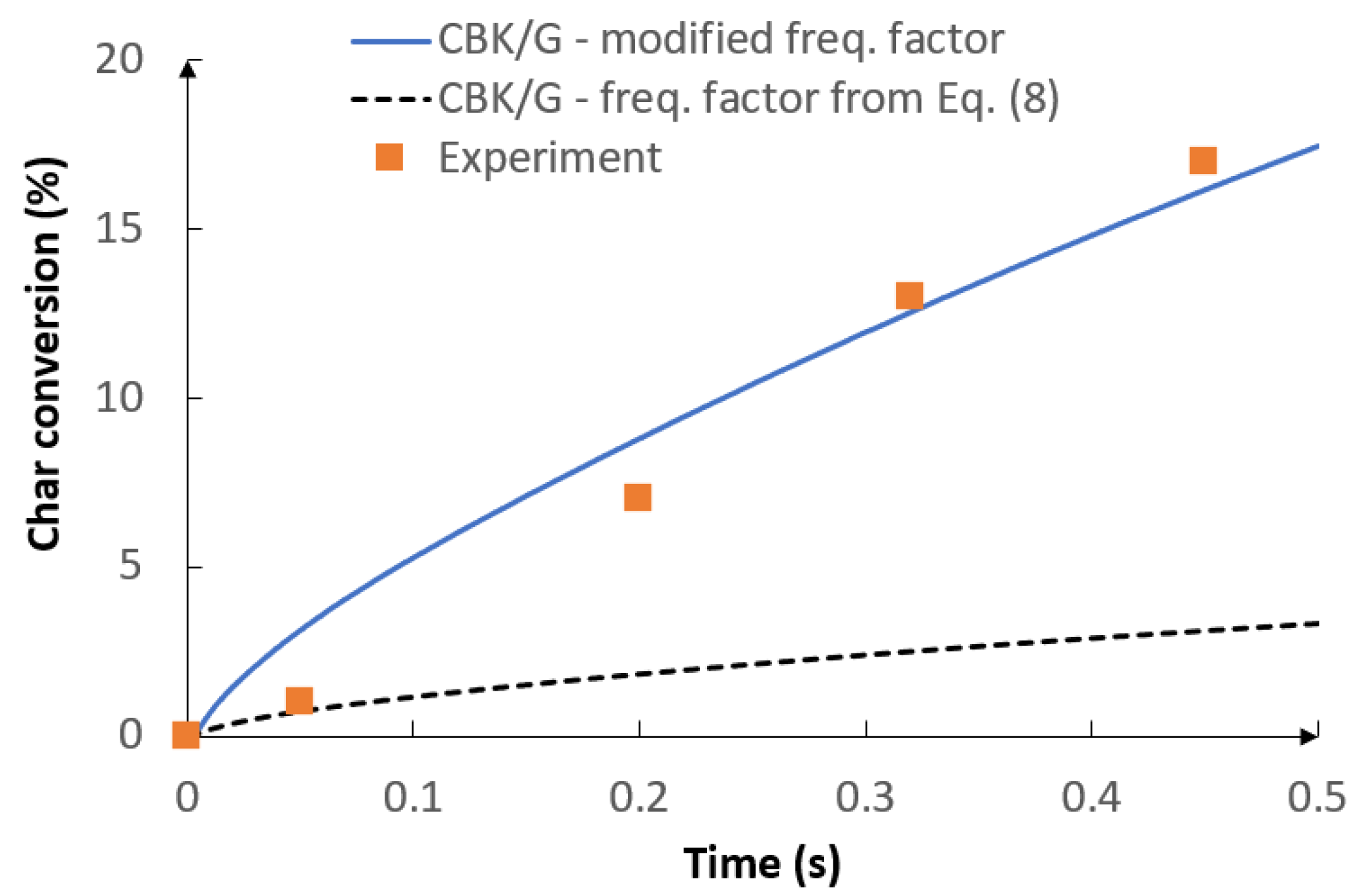
5.1. Optimization Procedure Results
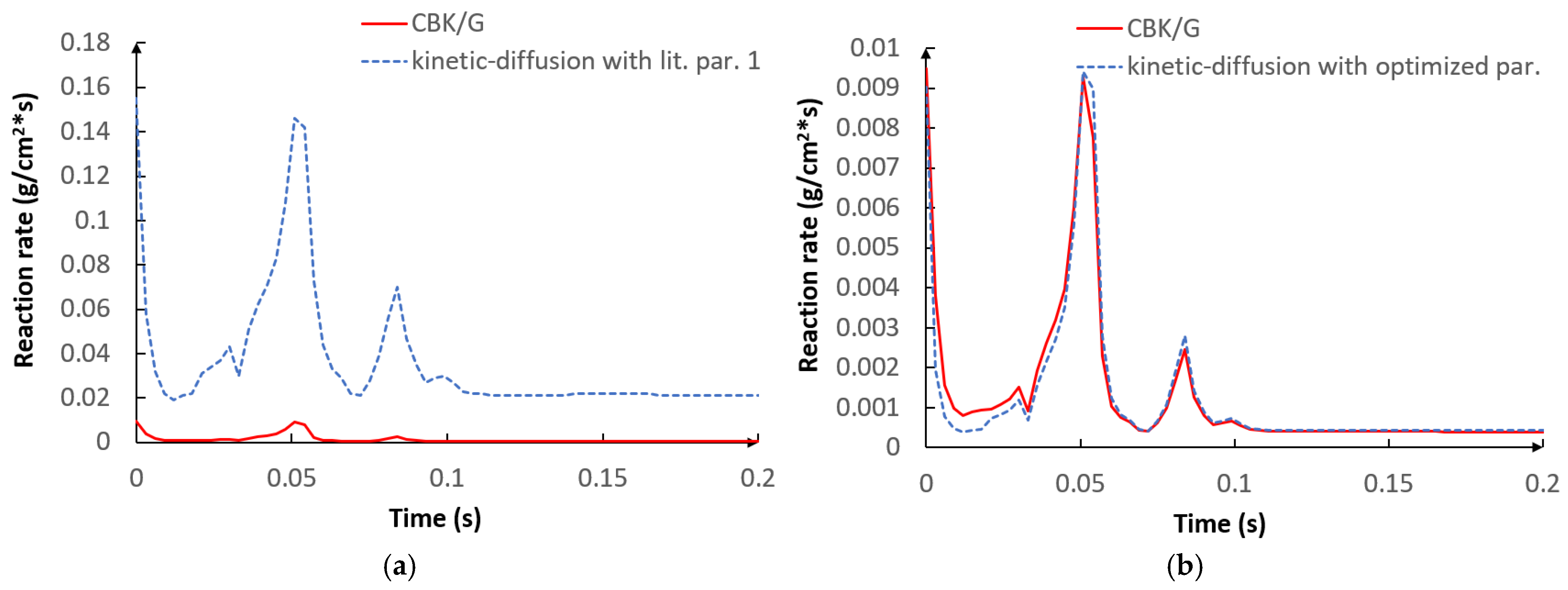
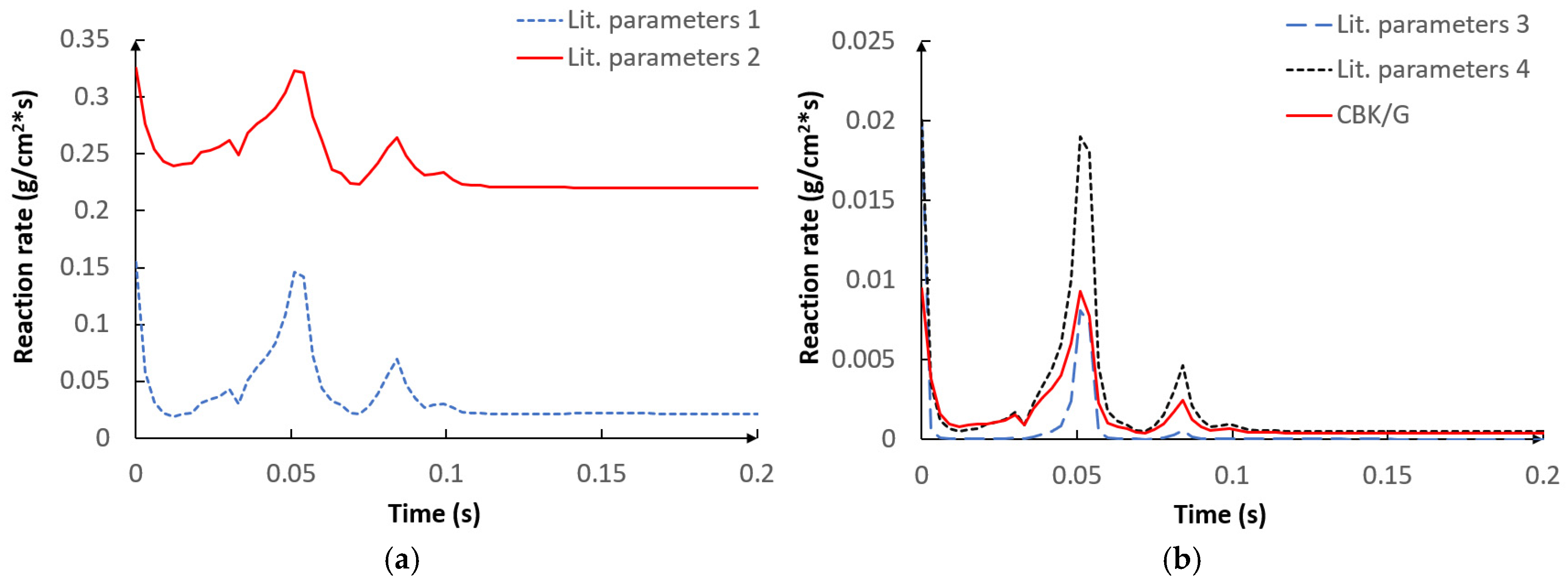
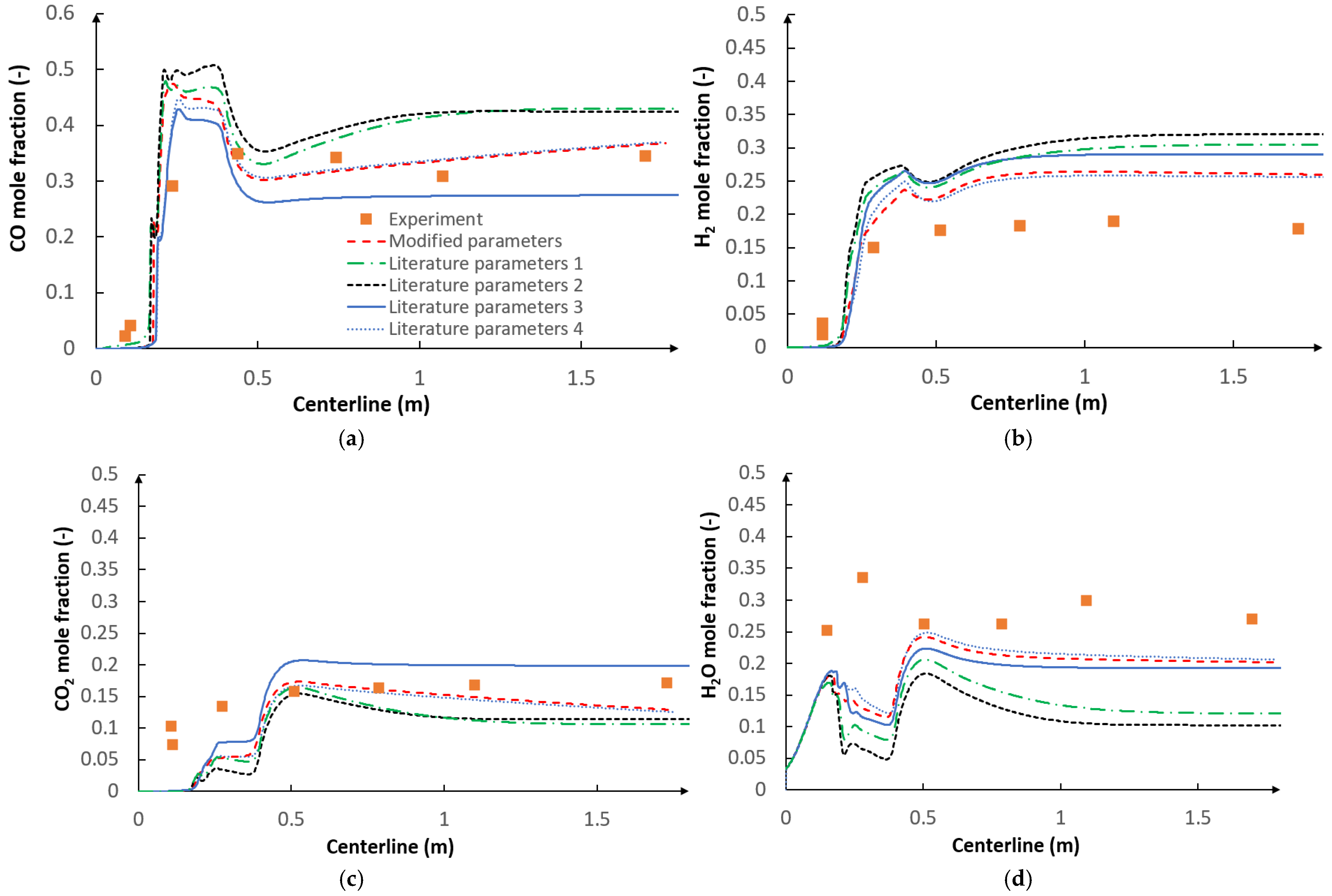
5.2. CFD Results
6. Conclusions
- The optimization procedure investigated in the current allows enhancing the modeling strategy by obtaining adjusted kinetic parameters of the kinetic-diffusion model only for the specific operating conditions.
- The use of the optimization procedure resulted in a better agreement between the model results and the experimental data in terms of the gas composition and char conversion factor. In order to further improve the accuracy of the procedure, future research should consider the application of the intrinsic-based char conversion models with Langmuir-Hinshelwood (LH) kinetics.
- The applied kinetic parameters of char-oxidation and char-gasification reactions proved to have a significant impact in the gasification process simulations. The major effect could be observed on the final gas composition and the char conversion factor, but also on the gas composition in the flame zone.
- Due to the versatile character of the method, the presented optimization procedure can be applied in other areas of interest, provided that both complex and simple models are available.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BYU | Brigham Young University |
| CBK | Carbon burnout kinetic model |
| CBK/E | Carbon burnout kinetic model for oxidation |
| CBK/G | Carbon burnout kinetic model for gasification |
| CFD | Computational fluid dynamics |
| C2SM | Competing two-step reaction model |
| Daf | Dry-ash-free |
| DNS | Direct numerical simulation |
| FG-DVC | Functional-group, depolymerization, vaporization, cross-linking model |
| LES | Large eddy simulation |
| LH | Langmuir-Hinshelwood kinetics |
| RANS | Reynolds averaged Navier-Stokes equations |
| SIMPLE | Semi-implicit method for pressure linked equations |
| WSGG | Weighted sum of gray gas model |
References
- EIA. Today in Energy—U.S. Energy Information Administration (EIA). Available online: https://www.eia.gov/todayinenergy/detail.php?id=26912 (accessed on 8 October 2020).
- Worldometer. World Coal Statistics—Worldometer. Available online: https://www.worldometers.info/coal/ (accessed on 8 October 2020).
- IEA. Emissions—Global Energy & CO2 Status Report 2019—Analysis. Available online: https://www.iea.org/reports/global-energy-co2-status-report-2019/emissions (accessed on 8 October 2020).
- Pawlak-Kruczek, H.; Wnukowski, M.; Niedzwiecki, L.; Czerep, M.; Kowal, M.; Krochmalny, K.; Zgóra, J.; Ostrycharczyk, M.; Baranowski, M.; Tic, W.J.; et al. Torrefaction as a valorization method used prior to the gasification of sewage sludge. Energies 2019, 12, 175. [Google Scholar] [CrossRef] [Green Version]
- Luo, H.; Niedzwiecki, L.; Arora, A.; Mościcki, K.; Pawlak-Kruczek, H.; Krochmalny, K.; Baranowski, M.; Tiwari, M.; Sharma, A.; Sharma, T.; et al. Influence of torrefaction and pelletizing of sawdust on the design parameters of a fixed bed gasifier. Energies 2020, 13, 3018. [Google Scholar] [CrossRef]
- NETL. IGCC Efficiency/Performance. Available online: https://www.netl.doe.gov/research/Coal/energy-systems/gasification/gasifipedia/igcc-efficiency (accessed on 10 February 2021).
- Li, J.; Paul, M.C.; Younger, P.L.; Watson, I.; Hossain, M.; Welch, S. Combustion modelling of pulverized biomass particles at high temperatures. Phys. Procedia 2015, 66, 273–276. [Google Scholar] [CrossRef] [Green Version]
- Klimanek, A.; Adamczyk, W.P.; Katelbach-Woźniak, A.; Węcel, G.; Szlęk, A. Towards a hybrid Eulerian–Lagrangian CFD modeling of coal gasification in a circulating fluidized bed reactor. Fuel 2015, 152, 131–137. [Google Scholar] [CrossRef]
- Drikakis, D.; Frank, M.; Tabor, G. Multiscale computational fluid dynamics. Energies 2019, 12, 3272. [Google Scholar] [CrossRef] [Green Version]
- Della Torre, A.; Montenegro, G.; Onorati, A.; Khadilkar, S.; Icarelli, R. Multi-scale CFD modeling of plate heat exchangers including offset-strip fins and dimple-type turbulators for automotive applications. Energies 2019, 12, 2965. [Google Scholar] [CrossRef] [Green Version]
- Sutardi, T.; Wang, L.; Karimi, N.; Paul, M.C. Utilization of H2O and CO2 in coal particle gasification with an impact of temperature and particle size. Energy Fuels 2020, 34, 12841–12852. [Google Scholar] [CrossRef]
- Pour, M.S.; Weihong, Y. Performance of pulverized coal combustion under high temperature air diluted by steam. ISRN Mech. Eng. 2014, 2014, 217574. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Qiao, L. Mathematical modeling of coal gasification processes in a well-stirred reactor: Effects of devolatilization and moisture content. Energy Fuels 2012, 26, 5759–5768. [Google Scholar] [CrossRef]
- Mularski, J.; Modliński, N. Entrained flow coal gasification process simulation with the emphasis on empirical devolatilization models optimization procedure. Appl. Therm. Eng. 2020, 175, 115401. [Google Scholar] [CrossRef]
- Vascellari, M.; Arora, R.; Pollack, M.; Hasse, C. Simulation of entrained flow gasification with advanced coal conversion submodels. Part 1: Pyrolysis. Fuel 2013, 113, 654–669. [Google Scholar] [CrossRef]
- Mularski, J.; Modliński, N. Impact of Chemistry–Turbulence Interaction Modeling Approach on the CFD Simulations of Entrained Flow Coal Gasification. Energies 2020, 13, 6467. [Google Scholar] [CrossRef]
- Mularski, J.; Pawlak-Kruczek, H.; Modlinski, N. A review of recent studies of the CFD modelling of coal gasification in entrained flow gasifiers, covering devolatilization, gas-phase reactions, surface reactions, models and kinetics. Fuel 2020, 271, 117620. [Google Scholar] [CrossRef]
- Baum, M.M.; Street, P.J. Predicting the combustion behaviour of coal particles. Combust. Sci. Technol. 1971, 3, 231–243. [Google Scholar] [CrossRef]
- Smith, I. The combustion rates of coal chars: A review. Symp. Combust. 1982, 19, 1045–1065. [Google Scholar] [CrossRef]
- Niksa, S.; Liu, G.-S.; Hurt, R.H. Coal conversion submodels for design applications at elevated pressures. Part I. Devolatilization and char oxidation. Prog. Energy Combust. Sci. 2003, 29, 425–477. [Google Scholar] [CrossRef]
- Liu, G.-S.; Niksa, S. Coal conversion submodels for design applications at elevated pressures. Part II. Char gasification. Prog. Energy Combust. Sci. 2004, 30, 679–717. [Google Scholar] [CrossRef]
- Halama, S.; Spliethoff, H. Numerical simulation of entrained flow gasification: Reaction kinetics and char structure evolution. Fuel Process. Technol. 2015, 138, 314–324. [Google Scholar] [CrossRef]
- Silaen, A.; Wang, T. Comparison of instantaneous, equilibrium, and finite-rate gasification models in an entrained-flow coal gasifier. In Proceedings of the 26th Annual International Pittsburgh Coal Conference 2009, Pittsburgh, PA, USA, 20–23 September 2009; pp. 1–11. [Google Scholar]
- Lu, X.; Wang, T. Water–gas shift modeling in coal gasification in an entrained-flow gasifier—Part 2: Gasification application. Fuel 2013, 108, 620–628. [Google Scholar] [CrossRef]
- Liu, H.; Kojima, T. Theoretical study of coal gasification in a 50 ton/day HYCOL entrained flow gasifier. I. Effects of coal properties and implications. Energy Fuels 2004, 18, 908–912. [Google Scholar] [CrossRef]
- Liu, H.; Kojima, T. Theoretical study of coal gasification in a 50 ton/day HYCOL entrained flow gasifier. II. Effects of operating conditions and comparison with pilot-scale experiments. Energy Fuels 2004, 18, 913–917. [Google Scholar] [CrossRef]
- Khan, J.R.; Wang, T. Implementation of a demoisturization and devolatilization model in multi-phase simulation of a hybrid entrained-flow and fluidized bed mild gasifier. Int. J. Clean Coal Energy 2013, 2, 35–53. [Google Scholar] [CrossRef]
- Lu, X.; Wang, T. Investigation of radiation models in entrained-flow coal gasification simulation. Int. J. Heat Mass Transf. 2013, 67, 377–392. [Google Scholar] [CrossRef]
- Lu, X.; Wang, T. Investigation of low rank coal gasification in a two-stage downdraft entrained-flow gasifier. Int. J. Clean Coal Energy 2014, 3, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.; Horio, M.; Kojima, T. Numerical simulation of entrained flow coal gasifiers. Part I: Modeling of coal gasification in an entrained flow gasifier. Fuel 2000, 55, 3861–3874. [Google Scholar] [CrossRef]
- Labbafan, A.; Ghassemi, H. Numerical modeling of an E-Gas entrained flow gasifier to characterize a high-ash coal gasification. Energy Convers. Manag. 2016, 112, 337–349. [Google Scholar] [CrossRef]
- Chen, C.; Horio, M.; Kojima, T. Numerical simulation of entrained flow coal gasifiers. Part II: Effects of operating conditions on gasifier performance. Chem. Eng. Sci. 2000, 55, 3861–3874. [Google Scholar] [CrossRef]
- Chen, C.; Horio, M.; Kojima, T. Use of numerical modeling in the design and scale-up of entrained flow coal gasifiers. Fuel 2001, 80, 1513–1523. [Google Scholar] [CrossRef]
- Luan, Y.-T.; Chyou, Y.-P.; Wang, T. Numerical analysis of gasification performance via finite-rate model in a cross-type two-stage gasifier. Int. J. Heat Mass Transf. 2013, 57, 558–566. [Google Scholar] [CrossRef]
- Ajilkumar, A.; Sundararajan, T.; Shet, U. Numerical modeling of a steam-assisted tubular coal gasifier. Int. J. Therm. Sci. 2009, 48, 308–321. [Google Scholar] [CrossRef]
- Brown, B.W.; Smoot, L.D.; Smith, P.J.; Hedman, P.O. Measurement and prediction of entrained-flow gasification processes. AIChE J. 1988, 34, 435–446. [Google Scholar] [CrossRef]
- Ansys Fluent—Fluid Simulation Software: User Guide 2020 (R2). Available online: https://ansyshelp.ansys.com/account/secured?returnurl=/Views/Secured/prod_page.html?pn=Fluent&prodver=20.2&lang=en (accessed on 9 March 2020).
- Patankar, S.; Spalding, D. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows. Int. J. Heat Mass Transf. 1972, 15, 1787–1806. [Google Scholar] [CrossRef]
- Crowe, C.T.; Sharma, M.P.; Stock, D.E. The particle-source-in cell (PSI-CELL) model for gas-droplet flows. J. Fluids Eng. 1977, 99, 325–332. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Dukowicz, J.K. A particle-fluid numerical model for liquid sprays. J. Comput. Phys. 1980, 35, 229–253. [Google Scholar] [CrossRef]
- Kumar, M.; Ghoniem, A.F. Multiphysics simulations of entrained flow gasification. Part II: Constructing and validating the overall model. Energy Fuels 2012, 26, 464–479. [Google Scholar] [CrossRef]
- Kobayashi, H.; Howard, J.; Sarofim, A. Coal devolatilization at high temperatures. Symp. Combust. 1977, 16, 411–425. [Google Scholar] [CrossRef]
- Magnussen, B.; Hjertager, B. On mathematical modeling of turbulent combustion with special emphasis on soot formation and combustion. Symp. Combust. 1977, 16, 719–729. [Google Scholar] [CrossRef]
- Gosman, A.D.; Ioannides, E. Aspects of computer simulation of liquid-fuelled combustors. J. Energy 1983, 7, 482–490. [Google Scholar] [CrossRef]
- Czajka, K.M.; Modliński, N.; Kisiela-Czajka, A.M.; Naidoo, R.; Peta, S.; Nyangwa, B. Volatile matter release from coal at different heating rates –experimental study and kinetic modelling. J. Anal. Appl. Pyrolysis 2019, 139, 282–290. [Google Scholar] [CrossRef]
- Zhang, Z.; Lu, B.; Zhao, Z.; Zhang, L.; Chen, Y.; Li, S.; Luo, C.; Zheng, C. CFD modeling on char surface reaction behavior of pulverized coal MILD-oxy combustion: Effects of oxygen and steam. Fuel Process. Technol. 2020, 204, 106405. [Google Scholar] [CrossRef]
- Lu, M.; Xiong, Z.; Li, J.; Li, X.; Fang, K.; Li, T. Catalytic steam reforming of toluene as model tar compound using Ni/coal fly ash catalyst. Asia Pac. J. Chem. Eng. 2020, 15, e2529. [Google Scholar] [CrossRef]
- Hurt, R.; Sun, J.-K.; Lunden, M. A kinetic model of carbon burnout in pulverized coal combustion. Combust. Flame 1998, 113, 181–197. [Google Scholar] [CrossRef]
- Hurt, R.H.; Lunden, M.M.; Brehob, E.G.; Maloney, D.J. Statistical kinetics for pulverized coal combustion. Symp. Combust. 1996, 26, 3169–3177. [Google Scholar] [CrossRef] [Green Version]
- Hurt, R.H.; Calo, J.M. Semi-global intrinsic kinetics for char combustion modeling Entry 2 has also been referred to as “Langmuir kinetics”. The present paper adopts common chemical engineering usage, in which the designation “Langmuir” is applied to the equilibrium adsorption. Combust. Flame 2001, 125, 1138–1149. [Google Scholar] [CrossRef]
- Lang, T.; Hurt, R.H. Char combustion reactivities for a suite of diverse solid fuels and char-forming organic model compounds. Proc. Combust. Inst. 2002, 29, 423–431. [Google Scholar] [CrossRef]
- Vascellari, M.; Arora, R.; Hasse, C. Simulation of entrained flow gasification with advanced coal conversion submodels. Part 2: Char conversion. Fuel 2014, 118, 369–384. [Google Scholar] [CrossRef]
- Jones, W.; Lindstedt, R. Global reaction schemes for hydrocarbon combustion. Combust. Flame 1988, 73, 233–249. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Dryer, F.L. Simplified reaction mechanisms for the oxidation of hydrocarbon fuels in flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Liu, G.-S.; Tate, A.; Bryant, G.W.; Wall, T. Mathematical modeling of coal char reactivity with CO2 at high pressures and temperatures. Fuel 2000, 79, 1145–1154. [Google Scholar] [CrossRef]
- Goetz, G.J.; Nsakala, N.Y.; Patel, R.L.; Lao, T.C. Combustion and Gasification Characteristics of Chars from Four Commercially Significant Coals of Different Rank; Electric Power Research Institute: Palo Alto, CA, USA, 1982. [Google Scholar]
- Keller, F.; Küster, F.; Meyer, B. Determination of coal gasification kinetics from integral drop tube furnace experiments with steam and CO2. Fuel 2018, 218, 425–438. [Google Scholar] [CrossRef]
- Everson, R.C.; Neomagus, H.W.; Kasaini, H.; Njapha, D. Reaction kinetics of pulverized coal-chars derived from inertinite-rich coal discards: Gasification with carbon dioxide and steam. Fuel 2006, 85, 1076–1082. [Google Scholar] [CrossRef]
- Huang, Z.; Zhang, J.; Zhao, Y.; Zhang, H.; Yue, G.; Suda, T.; Narukawa, M. Kinetic studies of char gasification by steam and CO2 in the presence of H2 and CO. Fuel Process. Technol. 2010, 91, 843–847. [Google Scholar] [CrossRef]
- Holstein, A.; Bassilakis, R.; Wójtowicz, M.A.; Serio, M.A. Kinetics of methane and tar evolution during coal pyrolysis. Proc. Combust. Inst. 2005, 30, 2177–2185. [Google Scholar] [CrossRef]
- De Jong, W.; Di Nola, G.; Venneker, B.C.H.; Spliethoff, H.; Wójtowicz, M.A. TG-FTIR pyrolysis of coal and secondary biomass fuels: Determination of pyrolysis kinetic parameters for main species and NOxprecursors. Fuel 2007, 86, 2367–2376. [Google Scholar] [CrossRef]
- Várhegyi, G. Aims and methods in non-isothermal reaction kinetics. J. Anal. Appl. Pyrolysis 2007, 79, 278–288. [Google Scholar] [CrossRef] [Green Version]
- Scaccia, S. TG–FTIR and kinetics of devolatilization of Sulcis coal. J. Anal. Appl. Pyrolysis 2013, 104, 95–102. [Google Scholar] [CrossRef]
- Czajka, K.; Kisiela, A.; Moroń, W.; Ferens, W.; Rybak, W. Pyrolysis of solid fuels: Thermochemical behaviour, kinetics and compensation effect. Fuel Process. Technol. 2016, 142, 42–53. [Google Scholar] [CrossRef]





| Models | |
|---|---|
| Devolatilization: | Competing two-step reaction mechanism (C2SM) [43] |
| Gas phase: | Global reaction approach with finite-rate/eddy dissipation model [44] |
| Char conversion: | Kinetic-diffusion model [19] |
| Turbulence: | Realizable k-ε model [40] |
| Radiation: | Discrete ordinate method [37], weighted sum of gray gas model [37] |
| Particle tracking: | Discrete phase model, Discrete random walk model [41] |
| Particle models: | Spherical particle drag law [45], Rosin-Rammler particle size distribution, Wet combustion [37], Particle radiation interaction [37] |
| Pressure-velocity coupling | Semi-implicit method for pressure linked equations (SIMPLE) [38] |
| Proximate Analysis, % as Received | |
| Volatile matter | 45.6 |
| Fixed carbon | 43.7 |
| Ash | 8.3 |
| Moisture | 2.4 |
| Ultimate Analysis, % Dry-Ash-Free | |
| C | 77.6 |
| H | 6.56 |
| N | 1.42 |
| S | 0.55 |
| 1st Stream, kg/h | 26.24 |
| O2 | 0.85 |
| Ar | 0.126 |
| H2O | 0.024 |
| 2nd Stream, kg/h | 6.62 |
| H2O | 1 |
| Utah Bituminous Coal, kg/h | 23.88 |
| Min. Diameter | Max. Diameter | Mean Diameter | Spread Parameter |
|---|---|---|---|
| dmin, µm | dmax, µm | , µm | n |
| 1 | 85 | 36 | 1.033 |
| Reactions: | Kinetic Parameters: A—kg/s Pa, E—J/kmol, α—No Unit |
|---|---|
| Devolatilization: | |
| Vol → 0.218C7H10.61O0.87 + 0.322CH6.33 + 0.309H2O + 0.127CO + 0.024CO2 x = 7, y = 10.61, z = 0.87 m = 1, n = 6.33 | |
| Gas-Phase Reactions: | |
[42] | |
[42] | |
[42] | |
[42] | |
| [46] [55] | |
[56] | |
[42] β = −1 | |
| Reactions | Kinetic Parameters A—kg/s Pa E—J/kmol β—No Unit | Literature Parameters No. 1 [30] | Optimized Parameters Based on CBK/E and CBK/G Models | Literature Parameters No. 2 [42] | Literature Parameters No. 3 [15] | Literature Parameters No. 4 [15] |
|---|---|---|---|---|---|---|
| C + 0.5O2 → CO | A | 0.052 | 2.3 | 0.005 | 0.005 | |
| E | ||||||
| β | 0 | 1.233 | 1 | 0 | 0 | |
| C + CO2 → 2CO | A | 0.066 | 4.4 | 0.3493 | 0.0635 | |
| E | ||||||
| β | 0 | −0.263 | 1 | 0 | 0 | |
| C + H2O → CO + H2 | A | 0.0782 | 1.33 | 61.484 | 0.0019 | |
| E | ||||||
| β | 0 | −0.124 | 1 | 0 | 0 |
| Char Conversion Degree % | |||
|---|---|---|---|
| Simulation Results Mean Particle Diameter 36 µm | Simulation Results All Particle Fractions 1–85 µm | Experiment All Particle Fractions 1–85 µm | |
| Literature parameters 1 | 100% | 100% | 82% |
| Optimized parameters | 83% | 77% | |
| Literature parameters 2 | 100% | 99% | |
| Literature parameters 3 | 27% | 59% | |
| Literature parameters 4 | 80% | 74% | |
| Kinetic Parameters | CO | H2 | CO2 | H2O | ||||
|---|---|---|---|---|---|---|---|---|
| Max Δe (%) | Av. Δe (%) | Max Δe (%) | Av. Δe (%) | Max Δe (%) | Av. Δe (%) | Max Δe (%) | Av. Δe (%) | |
| Lit. parameters 1 | 17.91 | 6.74 | 12.80 | 7.89 | 10.22 | 5.87 | 16.82 | 11.84 |
| Mod. parameters | 18.48 | 4.82 | 7.95 | 5.47 | 10.15 | 4.72 | 20.22 | 9.58 |
| Lit. parameters 2 | 20.20 | 7.94 | 14.40 | 8.98 | 10.15 | 5.98 | 19.73 | 13.04 |
| Lit. parameters 3 | 11.11 | 5.71 | 11.36 | 7.51 | 10.14 | 5.38 | 19.24 | 10.35 |
| Lit. parameters 4 | 12.50 | 4.90 | 8.33 | 5.40 | 10.16 | 4.77 | 20.68 | 8.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mularski, J.; Modliński, N. Entrained-Flow Coal Gasification Process Simulation with the Emphasis on Empirical Char Conversion Models Optimization Procedure. Energies 2021, 14, 1729. https://doi.org/10.3390/en14061729
Mularski J, Modliński N. Entrained-Flow Coal Gasification Process Simulation with the Emphasis on Empirical Char Conversion Models Optimization Procedure. Energies. 2021; 14(6):1729. https://doi.org/10.3390/en14061729
Chicago/Turabian StyleMularski, Jakub, and Norbert Modliński. 2021. "Entrained-Flow Coal Gasification Process Simulation with the Emphasis on Empirical Char Conversion Models Optimization Procedure" Energies 14, no. 6: 1729. https://doi.org/10.3390/en14061729
APA StyleMularski, J., & Modliński, N. (2021). Entrained-Flow Coal Gasification Process Simulation with the Emphasis on Empirical Char Conversion Models Optimization Procedure. Energies, 14(6), 1729. https://doi.org/10.3390/en14061729







