Modeling Dynamics of Diffusion Across Heterogeneous Social Networks: News Diffusion in Social Media
Abstract
:1. Introduction
2. Related Work
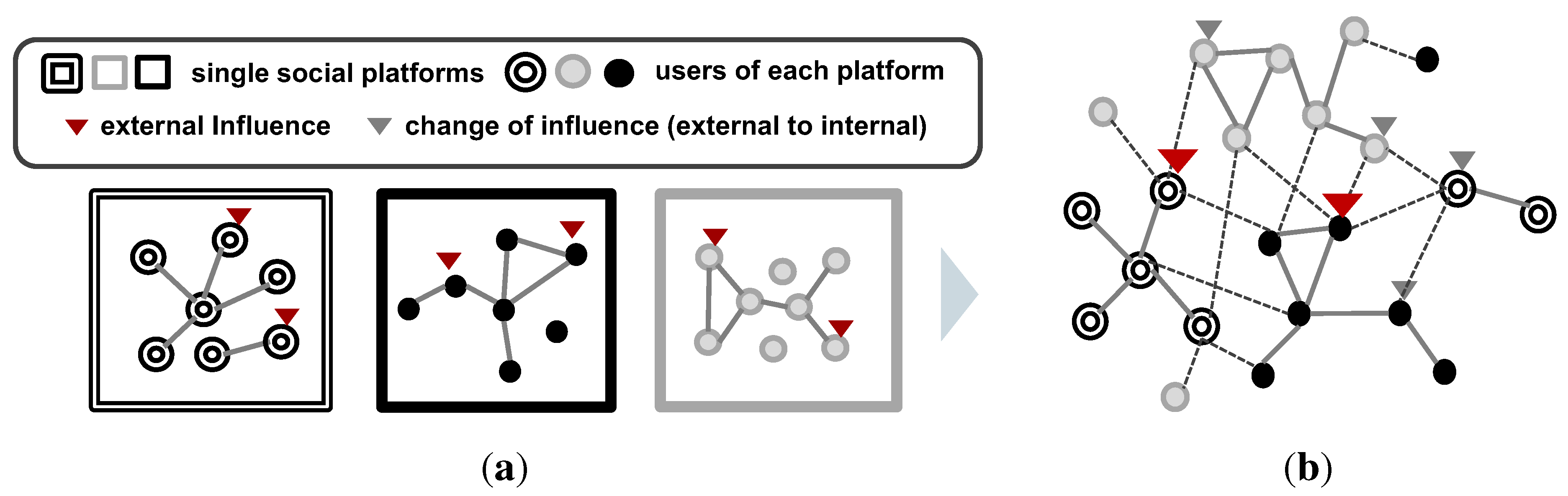
3. Conceptual Design for Diffusion across Heterogeneous Social Networks
4. Proposed Model
4.1. Fundamental Framework: Bass Model
4.2. Dynamic Influence Model
4.2.1. Problem Statement
4.2.2. Model Formulation
4.2.3. Comparison of Influence Assumptions
5. Preparation and Analysis of the Spinn3r Data Set
5.1. Target Data Selection
| Field | Description | Main Usage |
|---|---|---|
| Time | Publication time | To validate the direction of links from source to destination documents |
| Link | Document URL | To obtain document identity and extract domain name and/or user identity from regular patterns |
| Desc | Full HTML | To extract hyperlinks and written URLs in main text |
| Lang | Written language | To target English documents only |
| Type | Publisher type | To target documents of three media types (News, SNS, Blog) |

| Media Type | Domain | User Count |
|---|---|---|
| News | Second level domains (largest strongly connected network) | 9,225 |
| SNS | facebook.com | 4,560,800 |
| myspace.com | 822,998 | |
| flickr.com | 25,613 | |
| twitter.com | 6,169 | |
| posterous.com | 1,876 | |
| Blog | blogspot.com | 691,175 |
| livejournal.com | 158,361 | |
| wordpress.com | 90,803 | |
| tumblr.com | 23,967 | |
| typepad.com | 7,603 | |
| Total | 6,398,590 | |
5.2. Document Labeling with Real-world News


| Category | Real-world News Stories (January, 2011) |
|---|---|
| Politics (15) | Protests in Tunisia, Egypt, Sudan and Yemen; Internet shutdown in Egypt; Hosni Mubarak resignation; Tucson shooting; Julian Assange; US Healthcare law, etc. |
| Business and Economy (8) | US bank crisis; Apple profit record; Borders bankruptcy; New Google CEO; Swiss bank account revealed by Wikileaks; Food crisis, etc. |
| Technology and Science (13) | Apple iPad2 release; iPads for education; 10 billion downloads on the App Store; Wikipedia 10th Anniversary; Google technology news; Mammoth revive; Zodiac sign change; Betelgeuse, etc. |
| Disasters (4) | Floods in Australia, Sri Lanka and Brazil; Massive winter storm in US |
| Arts and Culture (17) | Academy Movie Awards; Golden Globe Awards; Screen Actors Guild Awards; Film release; Celebrities; Multiculturalism failure; Conflicts between Muslims and Christian; Cultural change of female education by Taliban; Chinese education, etc. |
| Sports (6) | NFL (National Football League) playoffs; BCS (Bowl Championship Series) Championship; AFC (Asian Football Confederation) Asian Cup; Australian Open; Ashes series winner; Sky Sport sexism scandal |
5.3. Global Spread of News in Social Media

6. Experiments
6.1. Experiments on Synthetic Data


| BM | DM | |
|---|---|---|
| Mean | 2.19e-3 | 3.74e-4 |
| STD | 8.77e-4 | 1.29e-4 |
| Train:Test = 60:40 | Train:Test = 80:20 | |||
|---|---|---|---|---|
| BM | DM | BM | DM | |
| Mean | 2.41e-3 | 1.83e-4 | 5.99e-4 | 4.2e-5 |
| STD | 2.16e-3 | 1.72e-4 | 6.06e-4 | 4.2e-5 |
| Meta-population 1 | Meta-population 2 | Meta-population 3 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Par. | |||||||||||||||
| Avg. | 3.1e-4 | 1.6e-2 | 2.8e-2 | 1.4e-2 | 2.0e-1 | 2.7e-4 | 2.0e-2 | 3.6e-2 | 1.6e-2 | 2.2e-1 | 3.6e-4 | 1.3e-2 | 2.4e-2 | 1.4e-2 | 4.1e-1 |
| Std. | 2.8e-4 | 1.9e-2 | 3.0e-2 | 1.4e-2 | 1.9e-1 | 2.6e-4 | 1.9e-2 | 3.4e-2 | 1.6e-2 | 2.3e-1 | 2.7e-4 | 1.2e-2 | 2.1e-2 | 1.4e-2 | 3.3e-1 |
6.2. Experiments on Real Data
| Model Fitting Error | Prediction Error | |||
|---|---|---|---|---|
| BM | DM | BM | DM | |
| Mean | 2.866e-2 | 2.259e-2 | 3.207e-2 | 2.481e-2 |
| STD | 1.902e-2 | 1.027e-2 | 3.698e-2 | 1.018e-2 |



7. Discussions
8. Conclusions
Conflicts of Interest
References
- Cha, M.; Pérez, J.; Haddadi, H. Flash Floods and Ripples: The Spread of Media Content through the Blogosphere. In Proceedings of the International AAAI Conference on Weblogs and Social Media, San Jose, CA, USA, 17–20 May 2009.
- Gomez-Rodriguez, M.; Leskovec, J.; Krause, A. Inferring networks of diffusion and influence. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 5, 21. [Google Scholar] [CrossRef]
- Kim, M.; Xie, L.; Christen, P. Event Diffusion Patterns in Social Media. In Proceedings of the International AAAI Conference on Weblogs and Social Media, Trinity College, Dublin, Ireland, 4–7 June 2012.
- Leskovec, J.; McGlohon, M.; Faloutsos, C.; Glance, N.; Hurst, M. Cascading Behavior in Large Blog Graphs. In Proceedings of the Seventh SIAM International Conference on Data Mining, Minneapolis, MN, USA, 26–28 April 2007.
- Leskovec, J.; Backstrom, L.; Kleinberg, J. Meme-Tracking and the Dynamics of the News Cycle. In Proceeding of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009; ACM: New York, NY, USA, 2009; pp. 497–506. [Google Scholar]
- Adar, E.; Adamic, L. Tracking Information Epidemics in Blogspace. In Proceedings of the IEEE/WIC/ACM International Conference on Web Intelligence, Compiegne, France, 19–22 September 2005; pp. 207–214.
- Gruhl, D.; Guha, R.; Liben-Nowell, D.; Tomkins, A. Information Diffusion through Blogspace. In Proceedings of the International Conference on World Wide Web, New York, NY, USA, 17–22 May 2004; ACM: New York, NY, USA, 2004; pp. 491–501. [Google Scholar]
- Kamath, K.Y.; Caverlee, J.; Cheng, Z.; Sui, D.Z. Spatial Influence vs. Community Influence: Modeling the Global Spread of Social Media. In Proceedings of the International Conference on Information and Knowledge Management, Kuala Lumpur, Malaysia, 24–26 July 2012; ACM: New York, NY, USA, 2012; pp. 962–971. [Google Scholar]
- Kwak, H.; Lee, C.; Park, H.; Moon, S. What is Twitter, a social network or a news media? In Proceedings of the International Conference on World Wide Web, Raleigh, NC, USA, 26–30 April 2010; ACM: New York, NY, USA, 2010; pp. 591–600. [Google Scholar]
- Myers, S.; Zhu, C.; Leskovec, J. Information Diffusion and External Influence in Networks. In Proceeding of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Beijing, China, 12–16 August 2012; ACM: New York, NY, USA, 2012; pp. 33–41. [Google Scholar]
- Romero, D.; Meeder, B.; Kleinberg, J. Differences in the Mechanics of Information Diffusion Across Topics: Idioms, Political Hashtags, and Complex Contagion on Twitter. In Proceedings of the International Conference on World Wide Web, Hyderabad, India, 28 March–1 April 2011; ACM: New York, NY, USA, 2011; pp. 695–704. [Google Scholar]
- Bass, F. Comments on “A New Product Growth for Model Consumer Durables”: The Bass model. Manag. Sci. 2004, 50, 1833–1840. [Google Scholar] [CrossRef]
- Guimera, R.; Uzzi, B.; Spiro, J.; Amaral, L. Team assembly mechanisms determine collaboration network structure and team performance. Science 2005, 308, 697–702. [Google Scholar] [CrossRef] [PubMed]
- Kumar, V.; Krishnan, T. Multinational diffusion models: An alternative framework. Market. Sci. 2002, 21, 318–330. [Google Scholar]
- Luu, M.; Lim, E.; Hoang, T.; Chua, F. Modeling Diffusion in Social Networks Using Network Properties. In Proceedings of the International AAAI Conferenceon Weblogs and Social Media, Dublin, Ireland, 4–7 June 2012.
- Barrat, A.; Barthlemy, M.; Vespignani, A. Dynamical Processes on Complex Networks; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Anagnostopoulos, A.; Kumar, R.; Mahdian, M. Influence and Correlation in Social Networks. In Proceeding of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, NV, USA, 24–27 August 2008; ACM: New York, NY, USA, 2008; pp. 7–15. [Google Scholar]
- Bass, F. A new product growth for model consumer durables. Manag. Sci. 1969, 15, 215–227. [Google Scholar] [CrossRef]
- Wikipedia Current Events Portal from January, 2011. Available online: http://en.wikipedia.org/wiki/January_2011 (accessed on 29 August 2011).
- Spinn3r Dataset. In Proceedings of International AAAI Conference on Weblogs and Social Media (ICWSM’11), Barcelona, Spain, 17–21 July 2011; Available online: http://www.icwsm.org/data/ (accessed on 29 August 2011).
- Katz, E. The two-step flow of communication: An up-to-date report on an hypothesis. Public Opin. Q. 1957, 21, 61–78. [Google Scholar] [CrossRef]
- Rogers, E. Diffusion of Innovations; The Free Press of Glencoe: New York, 1962. [Google Scholar]
- Mahajan, V.; Muller, E.; Bass, F. Diffusion of new products: Empirical generalizations and managerial uses. Market. Sci. 1995, 14, G79–G88. [Google Scholar] [CrossRef]
- Niu, S.C. A stochastic formulation of the Bass Model of new-product diffusion. Math. Probl. Eng. 2002, 8, 249–263. [Google Scholar] [CrossRef]
- Young, H.P. Innovation diffusion in heterogeneous populations: Contagion, social influence, and social learning. Am. Econ. Rev. 2009, 99, 1899–1924. [Google Scholar] [CrossRef]
- Bailey, N. The Mathematical Theory of Infectious Diseases and Its Applications, 2nd ed.; Hafner Press/MacMillian Pub. Co.: New York, USA, 1975; Volume 413. [Google Scholar]
- Newman, M. Networks: An Introduction; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Putsis, W., Jr.; Balasubramanian, S.; Kaplan, E.; Sen, S. Mixing behavior in cross-country diffusion. Market. Sci. 1997, 16, 354–369. [Google Scholar] [CrossRef]
- Pan, W.; Aharony, N.; Pentland, A. Composite Social Network for Predicting Mobile Apps Installation. In Proceedings of the AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 7–11 August 2011.
- Kuperman, M.; Abramson, G. Small world effect in an epidemiological model. Phys. Rev. Lett. 2001, 86, 2909–2912. [Google Scholar] [CrossRef] [PubMed]
- Schilling, M.; Phelps, C. Interfirm collaboration networks: The impact of large-scale network structure on firm innovation. Manag. Sci. 2007, 53, 1113–1126. [Google Scholar] [CrossRef]
- Sobkowicz, P.; Kaschesky, M.; Bouchard, G. Opinion Formation in the Social Web: Agent-Based Simulations of Opinion Convergence and Divergence. In Agents and Data Mining Interaction; Springer: Berlin, Heidelberg, Germany, 2012; pp. 288–303. [Google Scholar]
- Clauset, A.; Shalizi, C.R.; Newman, M.E. Power-law distributions in empirical data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Christen, P. Data Matching. In Data-Centric Systems and Applications; Springer: Berlin, Germany, 2012. [Google Scholar]
- Manning, C.; Raghavan, P.; Schutze, H. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008; Volume 1. [Google Scholar]
- OpenCalais API. Available online: http://www.opencalais.com/calaisAPI (accessed on 29 August 2011).
- Salton, G.; Wong, A.; Yang, C.S. A vector space model for automatic indexing. Commun. ACM 1975, 18, 613–620. [Google Scholar] [CrossRef]
- Kelley, C.T. Iterative Methods for Optimization; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Multiculturalism Has Failed in Britain. Available online: http://uk.reuters.com/article/2011/02/05/uk-britain-radicalisation-idUKTRE71401G20110205 (accessed on 29 August 2011).
Appendices
A. Proof of Equation (13)
B. Proof of Equation (15)
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kim, M.; Newth, D.; Christen, P. Modeling Dynamics of Diffusion Across Heterogeneous Social Networks: News Diffusion in Social Media. Entropy 2013, 15, 4215-4242. https://doi.org/10.3390/e15104215
Kim M, Newth D, Christen P. Modeling Dynamics of Diffusion Across Heterogeneous Social Networks: News Diffusion in Social Media. Entropy. 2013; 15(10):4215-4242. https://doi.org/10.3390/e15104215
Chicago/Turabian StyleKim, Minkyoung, David Newth, and Peter Christen. 2013. "Modeling Dynamics of Diffusion Across Heterogeneous Social Networks: News Diffusion in Social Media" Entropy 15, no. 10: 4215-4242. https://doi.org/10.3390/e15104215
APA StyleKim, M., Newth, D., & Christen, P. (2013). Modeling Dynamics of Diffusion Across Heterogeneous Social Networks: News Diffusion in Social Media. Entropy, 15(10), 4215-4242. https://doi.org/10.3390/e15104215




