Spatially-Explicit Bayesian Information Entropy Metrics for Calibrating Landscape Transformation Models
Abstract
:1. Introduction
2. Case Study Description
2.1. Sampling Methodology




2.2. Simulation Modeling Parameterization
3. Simulation Accuracy Assessment Methodology

3.1. Basic Definitions
| Observed | ||||
|---|---|---|---|---|
| Simulated | 0 | 1 | ||
| 0 | TN | FN | SN | |
| 1 | FP | TP | SP | |
| RN | RP | GT | ||




3.2. Bayesian Diagnostic and Predictive Metrics
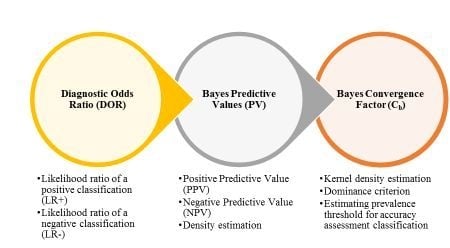
3.2.1. Diagnostic Odds Ratio (DOR)


3.2.2. Bayesian Predictive Values for Positive and Negative Classification (PPV/NPV)







3.2.3. Bayesian Convergence Factor (Cb)










4. Results and Discussion




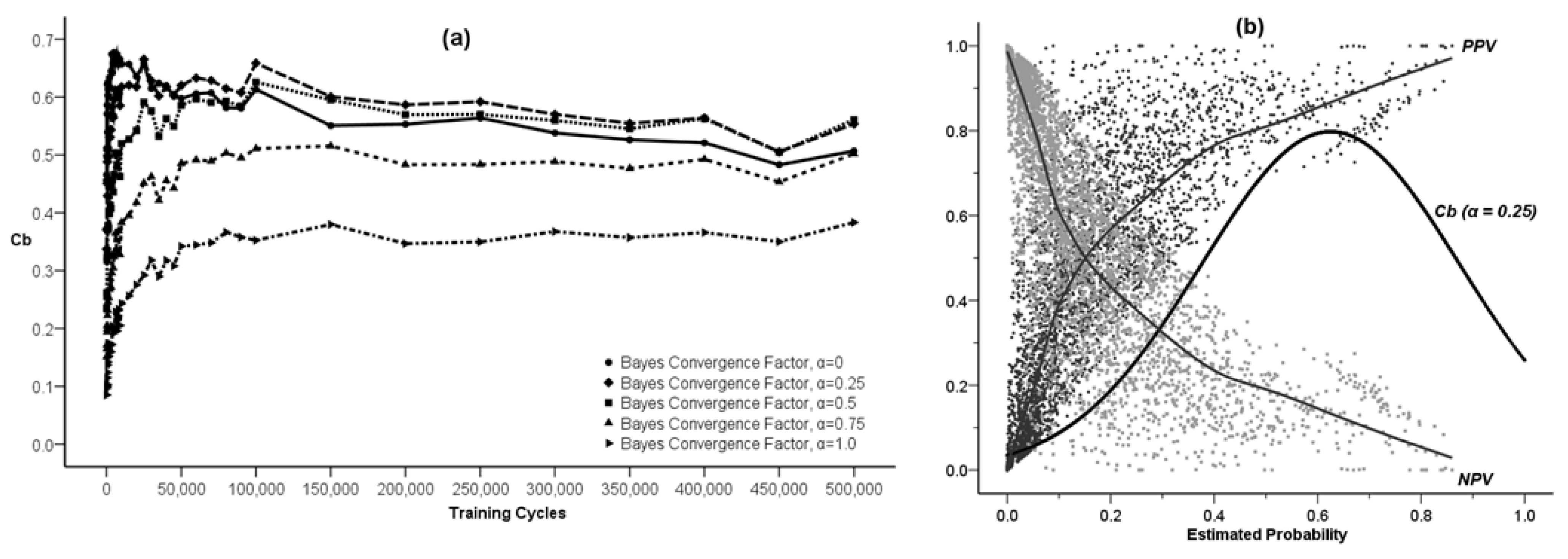
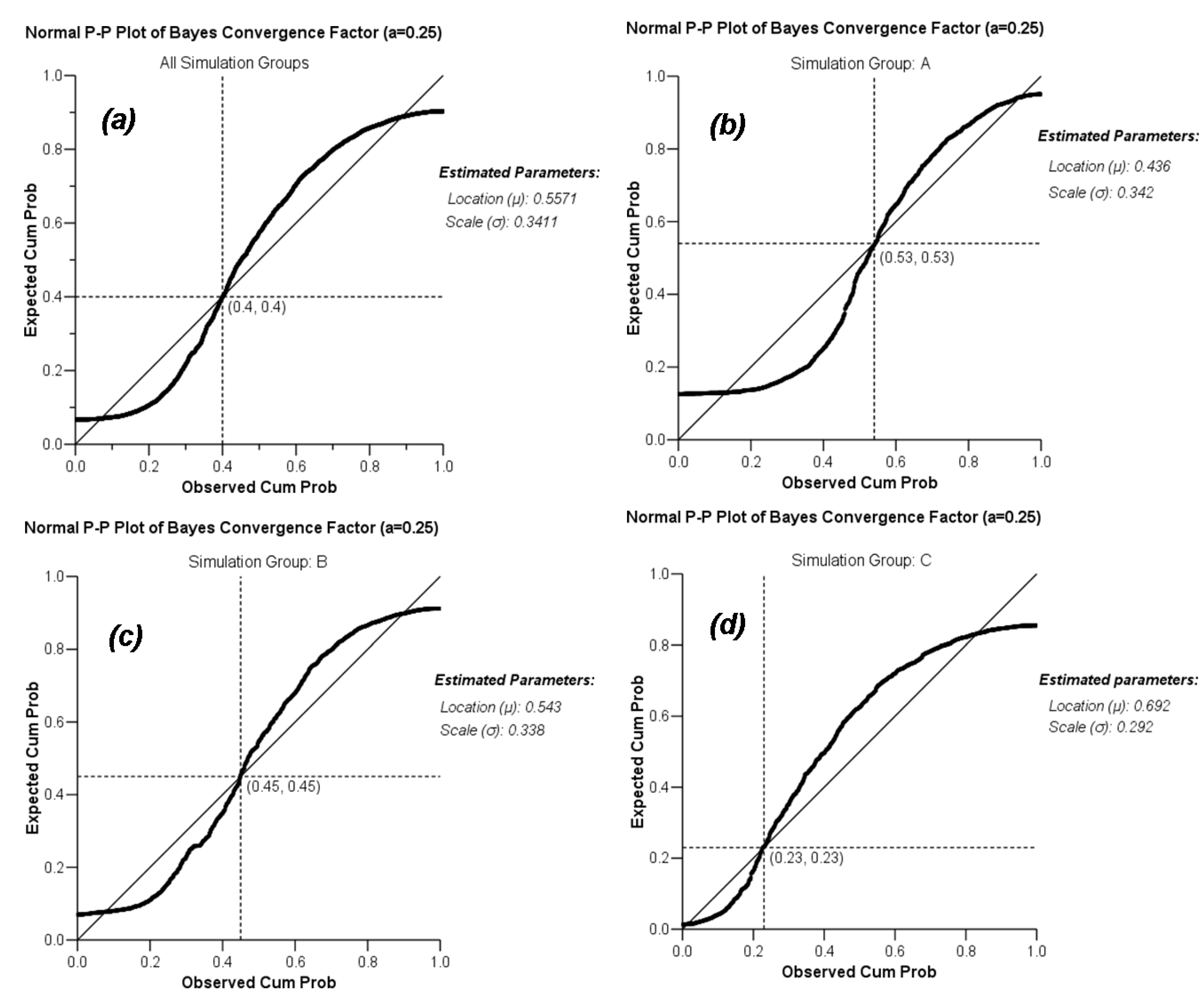
 using a maximum likelihood estimation (ML) method. The results of such an estimation for the varying degree of asymmetry in the Bayes convergence factor in the SEWI data are shown in Table 2. Two groups of parameter estimates are included in the analysis: (a) parameter estimates across all SEWI simulation training cycles, indicating a robust model performance; (b) parameter estimates only after 500,000 training cycles in the SEWI simulation runs, indicating a model performance with emphasis on maximizing the information flows in modeling transformations in our landscape.
using a maximum likelihood estimation (ML) method. The results of such an estimation for the varying degree of asymmetry in the Bayes convergence factor in the SEWI data are shown in Table 2. Two groups of parameter estimates are included in the analysis: (a) parameter estimates across all SEWI simulation training cycles, indicating a robust model performance; (b) parameter estimates only after 500,000 training cycles in the SEWI simulation runs, indicating a model performance with emphasis on maximizing the information flows in modeling transformations in our landscape.| Level | Predicted Values for Bayes Convergence Factor | ||
|---|---|---|---|
| Selection Level | Bayes Conversion Factor Asymmetry | Estimated location of Normal Distribution (μ) | Estimated scale of Normal Distribution (σ) |
| Across all training cycles | α = 0.0 | 0.5985 | 0.3027 |
| α = 0.25 | 0.5571 | 0.3411 | |
| α = 0.5 | 0.4764 | 0.3740 | |
| α = 0.75 | 0.3651 | 0.3685 | |
| α = 1.0 | 0.2443 | 0.3092 | |
| After 500,000 training cycles | α = 0.0 | 0.5067 | 0.3114 |
| α = 0.25 | 0.5537 | 0.3416 | |
| α = 0.5 | 0.5608 | 0.3861 | |
| α = 0.75 | 0.5019 | 0.4128 | |
| α = 1.0 | 0.3834 | 0.3772 | |


 : mean (location) criterion;
: mean (location) criterion; : variance (scale) criterion;
: variance (scale) criterion; : robustness criterion, and δ: any value or classification rule.
: robustness criterion, and δ: any value or classification rule.| Mean-Variance Groups | Robustness Groups | ||
| All training cycles | 500,000 training cycles | ||
| α = 0.0 | 1.071 | 0.071 | |
| α = 0.25 | 16.744 | 15.744 | |
| α = 0.5 | 0.286 | −0.714 | |
| α = 0.75 | 0.987 | −0.013 | |
| α = 1.0 | 1.596 | 0.596 | |
5. Conclusions
Acknowledgments
Conflict of Interest
References
- Lambin, E.F.; Geist, H. Land-Use and Land-Cover Change: Local Processes and Global Impacts; Springer-Verlag: Berlin, Germany, 2006. [Google Scholar]
- Pijanowski, B.C.; Robinson, K.D. Rates and patterns of land use change in the upper Great Lakes States, USA: A framework for spatial temporal analysis. Landscape Urban Plan. 2011, 102, 102–116. [Google Scholar] [CrossRef]
- Committee on grand challenges in environmental sciences, oversight commission for the committee on grand challenges in environmental sciences. Grand Challenges in Environmental Sciences; The National Academies Press: Washington, D.C., USA, 2001. [Google Scholar]
- Ray, D.K.; Pijanowksi, B.C.; Kendall, A.D.; Hyndman, D.W. Coupling land use and groundwater models to map land use legacies: Assessment of model uncertainties relevant to land use planning. Appl. Geogr. 2012, 34, 356–370. [Google Scholar] [CrossRef]
- Pijanowski, B.C.; Ray, D.K.; Kendall, A.D.; Duckles, J.M.; Hyndman, D.W. Using backcast land-use change and groundwater travel-time models to generate land-use legacy maps for watershed management. Ecol. Soc. 2007, 12, 25:1–25:19. [Google Scholar]
- Yang, G.; Bowling, L.C.; Chherkauer, K.A.; Pijanowksi, B.C. The impact of urban development on hydrologic regime from catchment to basin scales. Landscape Urban Plan. 2011, 103, 237–247. [Google Scholar] [CrossRef]
- Mishra, V.; Cherkauer, K.A.; Niyogi, D.; Lei, M.; Pijanowski, B.C.; Ray, D.K.; Bowling, L.C.; Yang, G. A regional scale assessment of land use/land cover and climatic changes on water and energy cycle in the upper Midwest United States. Int. J. Climatol. 2010, 30, 2025–2044. [Google Scholar] [CrossRef]
- Pijanowski, B.; Moore, N.; Mauree, D.; Niyogi, D. Evaluating error propagation in coupled land-atmosphere models. Earth Interact. 2011, 15, 1–25. [Google Scholar] [CrossRef]
- Wiley, M.J.; et al. A multi-modeling approach to evaluating climate and land use change impacts in a Great Lakes River Basin. Hydrobiologia 2010, 657, 243–262. [Google Scholar]
- Wayland, K.G.; Hyndman, D.W.; Boutt, D.; Pijanowski, B.C.; Long, D.T. Modeling the impact of historical land uses on surface water quality using ground water flow and solute transport models. Lakes Reserv. Res. Manag. 2002, 7, 189–199. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Boersma, W.; Castella, J.-C.; Clarke, K.; Nijs, T.D.; Dietzel, C.; Duan, Z.; Fostsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 2008, 42, 11–37. [Google Scholar]
- Pontius, R.G., Jr.; Neeti, N. Uncertainty in the difference between maps of future land change scenarios. Sustain. Sci. 2010, 5, 39–50. [Google Scholar] [CrossRef]
- Pijanowski, B.C.; Pithadia, S.; Shellito, B.A.; Alexandridis, K. Calibrating a neural network-based urban change model for two metropolitan areas of the upper midwest of the United States. Int. J. Geogr. Inf. Sci. 2005, 19, 197–215. [Google Scholar] [CrossRef]
- Pijanowski, B.C.; Alexandridis, K.T.; Müller, D. Modelling urbanization patterns in two diverse regions of the world. J. Land Use Sci. 2006, 1, 83–108. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423, Reprinted with corrections: 623–656, 1948. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. Mathematical Theory of Communication; University of Illinois Press: Chicago, IL, USA, 1963. [Google Scholar]
- Jessop, A. Informed Assessments: An Introduction to Information, Entropy, and Statistics; Ellis Horwood: New York, NY, USA, 1995; p. 366. [Google Scholar]
- Vajda, I. Theory of Statistical Inference and Information; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1989; p. 432. [Google Scholar]
- Stoica, P.; Selen, Y.; Li, J. Multi-model approach to model selection. Digit. Signal Process. 2004, 14, 399–412. [Google Scholar] [CrossRef]
- Nelson, T.; Boots, B.; Wulder, M.A. Techniques for accuracy assessment of tree locations extracted from remotely sensed imagery. J. Environ. Manag. 2005, 74, 265–271. [Google Scholar] [CrossRef] [PubMed]
- Roloff, G.J.; Haufler, J.B.; Scott, J.M.; Heglund, P.J.; Morrison, M.L.; Haufler, J.B.; Raphael, M.G.; Wall, W.A.; Samson, F.B. Modeling Habitat-based Viability from Organism to Population. In Predicting Species Occurences: Issues of Accuracy and Scale; Island Press: Washington, D.C., USA, 2002; pp. 673–686. [Google Scholar]
- James, F.C.; McGulloch, C.E.; Scott, J.M.; Heglund, P.J.; Morrison, M.L.; Haufler, J.B.; Raphael, M.G.; Wall, W.A.; Samson, F.B. Predicting Species Presence and Abundance. In Predicting Species Occurences: Issues of Accuracy and Scale; Island Press: Washington, D.C., USA, 2002; pp. 461–466. [Google Scholar]
- Gonzalez-Rebeles, C.; Thompson, B.C.; Bryant, F.C.; Scott, J.M.; Heglund, P.J.; Morrison, M.L.; Haufler, J.B.; Raphael, M.G.; Wall, W.A.; Samson, F.B. Influence of Selected Environmental Variables on GIS-Habitat Models Used for Gap Analysis. In Predicting Species Occurences: Issues of Accuracy and Scale; Island Press: Washington, D.C., USA, 2002; pp. 639–652. [Google Scholar]
- Lowell, K.; Jaton, A. Spatial Accuracy Assessment: Land Information Uncertainty in Natural Resources; Ann Arbor Press: Chelsea, MI, USA, 1999; p. 455. [Google Scholar]
- Cablk, M.; White, D.; Kiester, A.R.; Scott, J.M.; Heglund, P.J.; Morrison, M.L.; Haufler, J.B.; Raphael, M.G.; Wall, W.A.; Samson, F.B. Assessment of Spatial Autocorrelation in Empirical Models in Ecology. In Predicting Species Occurences: Issues of Accuracy and Scale; Island Press: Washington, D.C., USA, 2002; pp. 429–440. [Google Scholar]
- Wu, J.; Hobbs, R. Key issues and research priorities in landscape ecology: An idiosyncratic synthesis. Landscape Ecol. 2002, 17, 355–365. [Google Scholar] [CrossRef]
- McKenney, D.W.; Venier, L.A.; Heerdegen, A.; McCarthy, M.A.; Scott, J.M.; Heglund, P.J.; Morrison, M.L.; Haufler, J.B.; Raphael, M.G.; Wall, W.A.; et al. A Monte Carlo experiment for species mapping problems. In Predicting Species Occurences: Issues of Accuracy and Scale; Island Press: Washington, D.C., USA, 2002; pp. 377–382. [Google Scholar]
- Gelfand, A.E.; Schmidt, A.M.; Wu, S.; Silander, J.A.; Latimer, A.; Rebelo, A.G. Modelling species diversity through species level hierarchical modelling. J. R. Stat. Soc. Ser. C Appl. Stat. 2005, 54, 1–20. [Google Scholar] [CrossRef]
- Pontius, G.R., Jr.; Spencer, J. Uncertainty in extrapolations of predictive land-change models. Environ. Plan. B—Plan. Des. 2005, 32, 211–230. [Google Scholar]
- Sun, H.; Forsythe, W.; Waters, N. Modeling urban land use change and urban sprawl: Calgary, Alberta, Canada. Netw. Spat. Econ. 2007, 7, 353–376. [Google Scholar] [CrossRef]
- Berry, B.J.L.; Kiel, L.D.; Elliot, E. Adaptive agents, intelligence, and emergent human organization: Capturing complexity through agent-based modeling. Proc. Natl. Acad. Sci. U.S.A. 2002, 99, 7178–7188. [Google Scholar] [CrossRef] [PubMed]
- North, M.; Macal, C.; Campbell, P. Oh behave! Agent-based behavioral representations in problem solving environments. Future Gener. Comput. Syst. 2005, 21, 1192–1198. [Google Scholar]
- Alexandridis, K.T.; Pijanowski, B.C. Assessing multiagent parcelization performance in the mabel simulation model using monte carlo replication experiments. Environ. Plan. B—Plan. Des. 2007, 34, 223–244. [Google Scholar] [CrossRef]
- Brown, D.G.; Page, S.E.; Riolo, R.; Zellner, M.; Rand, W. Path dependence and the validation of agent-based spatial models of land use. Int. J. Geogr. Inf. Sci. 2005, 19, 153–174. [Google Scholar] [CrossRef]
- Fortin, M.J.; Boots, B.; Csillag, F.; Remmel, T.K. On the role of spatial stochastic models in understanding landscape indices in ecology. Oikos 2003, 102, 203–212. [Google Scholar] [CrossRef]
- Demetrius, L.; Matthias Gundlach, V.; Ochs, G. Complexity and demographic stability in population models. Theor. Popul. Biol. 2004, 65, 211–225. [Google Scholar] [CrossRef] [PubMed]
- Luijten, J.C. A systematic method for generating land use patterns using stochastic rules and basic landscape characteristics: Results for a Colombian hillside watershed. Agric. Ecosyst. Environ. 2003, 95, 427–441. [Google Scholar] [CrossRef]
- Boyen, X.; Koller, D. Approximate Learning of Dynamic Models. In Advances in Neural Information Processing Systems (NIPS 1998), Denver, Colorado, December 1998; MIT Press: Cambridge, MA, USA, 1999; pp. 396–402. [Google Scholar]
- Dubra, J.; Ok, E.A. A model of procedural decision making in the presence of risk. Int. Econ. Rev. 2002, 43, 1053–1080. [Google Scholar] [CrossRef]
- Lazrak, A.; Quenez, M.C. A generalized stochastic differential utility. Math. Oper. Res. 2003, 28, 154–180. [Google Scholar] [CrossRef]
- Fokoue, E.; Titterington, D.M. Mixtures of factor analysers, bayesian estimation and inference by stochastic simulation. Mach. Learn. 2003, 50, 73–94. [Google Scholar] [CrossRef]
- Kleijnen, J.P.C. An overview of the design and analysis of simulation experiments for sensitivity analysis. Eur. J. Oper. Res. 2005, 164, 287–300. [Google Scholar] [CrossRef]
- Aptekarev, A.I.; Dehesa, J.S.; Yanez, R.J. Spatial entropy of central potentials and strong asymptotics of orthogonal polynomials. J. Math. Phys. 1994, 35, 4423–4428. [Google Scholar] [CrossRef]
- Brink, A.D. Minimum spatial entropy threshold selection. IEEE Proc. Vis. Image Signal Process. 1995, 142, 128–132. [Google Scholar] [CrossRef]
- Batten, D.F. Complex landscapes of spatial interaction. Ann. Reg. Sci. 2001, 35, 81–111. [Google Scholar] [CrossRef]
- Chen, K.; Irwin, E.; Jayaprakash, C.; Warren, K. The emergence of racial segregation in an agent-based model of residential location: The role of competing preferences. Comput. Math. Organ. Theory 2005, 11, 333–338. [Google Scholar] [CrossRef]
- Yin, L.; Brian, M. Residential location and the biophysical environment: Exurban development agents in a heterogeneous landscape. Environ. Plan. B—Plan. Des. 2007, 34, 279–295. [Google Scholar] [CrossRef]
- Munroe, D.K. Exploring the determinants of spatial pattern in residential land markets: amenities and disamenities in Charlotte, NC, USA. Environ. Plan. B—Plan. Des. 2007, 34, 336–354. [Google Scholar] [CrossRef]
- Carrion-Flores, C.; Irwin, E.G. Determinants of residential land-use conversion and sprawl at the rural-urban fringe. Am. J. Agric. Econ. 2004, 86, 889–904. [Google Scholar] [CrossRef]
- Parker, D.C.; Meretsky, V. Measuring pattern outcomes in an agent-based model of edge-effect externalities using spatial metrics. Agric. Ecosyst. Environ. 2004, 101, 233–250. [Google Scholar] [CrossRef]
- Reginster, I.; Rounsevell, M. Scenarios of future urban land use in Europe. Environ. Plan. B—Plan. Des. 2006, 33, 619–636. [Google Scholar] [CrossRef]
- Veldkamp, A. Investigating land dynamics: Future research perspectives. J. Land Use Sci. 2009, 4, 5–14. [Google Scholar] [CrossRef]
- Pijanowski, B.C.; Shellito, B.; Pithadia, S.; Alexandridis, K. Forecasting and assessing the impact of urban sprawl in coastal watersheds along eastern Lake Michigan. Lakes Reser. Res. Manag. 2002, 7, 271–285. [Google Scholar] [CrossRef]
- Tayyebi, A.; Pekin, B.K.; Pijanowski, B.C.; Plourde, J.D.; Doucette, J.S.; Braun, D. Hierarchical modeling of urban growth across the conterminous USA: Developing meso-scale quantity drivers for the Land Transformation Model. J. Land Use Sci. 2012, 8, 1–21. [Google Scholar] [CrossRef]
- SEWRPC Digital Land Use Inventory; SouthEastern Wisconsin Regional Planning Commission (SEWRPC): Waukesha, WI, USA, 2000. Available http://maps.sewrpc.org/regionallandinfo/metadata/Land_Use_Inventory.htm (accessed on 24 June 2013).
- Pijanowski, B.C.; Brown, D.G.; Shellito, B.A.; Manik, G.A. Using neural networks and GIS to forecast land use changes: A land transformation model. Comput. Environ. Urban Syst. 2002, 26, 553–575. [Google Scholar] [CrossRef]
- Foody, G.M. Status of land cover classification accuracy assessment. Remote Sens. Environ. 2002, 80, 185–201. [Google Scholar] [CrossRef]
- Sousa, S.; Caeiro, S.; Painho, M. Assessment of map similarity of categorical maps using kappa statistics: The case of sado estuary. In Proceedings of ESIG 2002, Tagus Park, Oeiras, Portugal, 17–19 July 2002; Associacao de Utilizadores de Informacao Geografica: Tagus Park, Oeiras, Portugal, 2002. [Google Scholar]
- Brenner, H.; Gefeller, O. Variation of sensitivity, specificity, likelihood ratios and predictive values with disease prevalence. Stat. Med. 1997, 16, 981–991. [Google Scholar] [CrossRef]
- Suh, Y.T. Signal Detection in Noises of Unknown Powers Using Two-Input Receivers; University of Michigan: Ann Arbor, MI, USA, 1983; p. 153. [Google Scholar]
- Glas, A.S.; Lijmer, J.G.; Prins, M.H.; Bonsel, G.J.; Bossuyt, P.M.M. The diagnostic odds ratio: A single indicator of test performance. J. Clin. Epidemiol. 2003, 56, 1129–1135. [Google Scholar] [CrossRef]
- Pepe, M.S.; Janes, H.; Longton, G.; Leisenring, W.; Newcomb, P. Limitations of the odds ratio in gauging the performance of a diagnostic, prognostic, or screening marker. Am. J. Epidemiol. 2004, 159, 882–890. [Google Scholar] [CrossRef] [PubMed]
- Schafer, J.; Strimmer, K. An empirical Bayes approach to inferring large-scale gene association networks. Bioinformatics 2005, 21, 754–764. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.E.; Winkler, R.L.; Fryback, D.G. The first positive: Computing positive predictive value at the extremes. Ann. Intern. Med. 2000, 132, 804–809. [Google Scholar] [CrossRef] [PubMed]
- Hart, J.D.; Wehrly, T.E. Kernel regression estimation using repeated measurements data. J. Am. Stat. Assoc. 1986, 81, 1080–1088. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: London, UK, 1986; p. 175. [Google Scholar]
- Simonoff, J.S. Smoothing methods in statistics; Springer: New York, NY, USA, 1996; p. 338. [Google Scholar]
- Tapia, R.A.; Thompson, J.R. Nonparametric probability density estimation; Johns Hopkins University Press: Baltimore, MD, USA, 1978; p. 176. [Google Scholar]
- Wand, M.P.; Jones, M.C. Kernel Smoothing; Chapman & Hall: London, UK, 1995; p. 212. [Google Scholar]
- Smyth, P. Probability density estimation and local basis function neural networks. In Computational Learning Theory and Natural Learning Systems; Hanson, S.J., Petsche, T., Rivest, R.L., Kearns, M., Eds.; MIT Press: Cambridge, MA, USA, 1994; Volume II, pp. 233–248. [Google Scholar]
- Hansen, B.E. Sample splitting and threshold estimation. Econometrica 2000, 68, 575–603. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Alexandridis, K.; Pijanowski, B.C. Spatially-Explicit Bayesian Information Entropy Metrics for Calibrating Landscape Transformation Models. Entropy 2013, 15, 2480-2509. https://doi.org/10.3390/e15072480
Alexandridis K, Pijanowski BC. Spatially-Explicit Bayesian Information Entropy Metrics for Calibrating Landscape Transformation Models. Entropy. 2013; 15(7):2480-2509. https://doi.org/10.3390/e15072480
Chicago/Turabian StyleAlexandridis, Kostas, and Bryan C. Pijanowski. 2013. "Spatially-Explicit Bayesian Information Entropy Metrics for Calibrating Landscape Transformation Models" Entropy 15, no. 7: 2480-2509. https://doi.org/10.3390/e15072480
APA StyleAlexandridis, K., & Pijanowski, B. C. (2013). Spatially-Explicit Bayesian Information Entropy Metrics for Calibrating Landscape Transformation Models. Entropy, 15(7), 2480-2509. https://doi.org/10.3390/e15072480