Abstract
We present an application of distributed consensus algorithms to metamorphic systems. A metamorphic system is a set of identical units that can self-assemble to form a rigid structure. For instance, one can think of a robotic arm composed of multiple links connected by joints. The system can change its shape in order to adapt to different environments via reconfiguration of its constituting units. We assume in this work that several metamorphic systems form a network: two systems are connected whenever they are able to communicate with each other. The aim of this paper is to propose a distributed algorithm that synchronizes all of the systems in the network. Synchronizing means that all of the systems should end up having the same configuration. This aim is achieved in two steps: (i) we cast the problem as a consensus problem on a metric space; and (ii) we use a recent distributed consensus algorithm that only makes use of metrical notions.
Keywords:
metamorphic systems 1. Introduction
Many problems in robotics, computer science and biology involve systems that can be described as reconfigurable or metamorphic. These systems change their state through a set of local rules, and in order to move from a given State A to another given State B, the system has to determine the sequence of local moves that it should perform. Examples of such systems are: metamorphic manufacturing systems [1], phylogenetic trees [2] and metamorphic robots [3].
The examples we will deal with in this paper will be about metamorphic robots, which consists of a collection of individual modules that can connect/disconnect from each other and form a rigid structure, referred to as a configuration or a state. Individual modules can change their position relative to their neighbors, as long as the whole system remains connected and according to a set of local rules. This allows the system to dynamically change its configuration and position. We assume here that we have many identical metamorphic robots that are able to communicate with each other and share information about their respective states. These robots form a communication network that we will assume to be decentralized (i.e., without a central fusion node). We are interested in the problem of distributed consensus among metamorphic systems: each system is in its own initial state, and we would like all of them to end up in a common configuration.
Distributed consensus algorithms have been thoroughly studied, mainly in the cases of vector data [4–6] or ordered data (e.g., [7]). The algorithm in [5], for example, is a distributed algorithm that uses pairwise arithmetic averages of the data. However, without specific assumptions, configurations cannot be averaged. The algorithm presented in [7] relies on pairwise maximum computations. In the setting of metamorphic robots, however, configurations cannot be easily ordered, hence the need to find an appropriate framework.
In [8,9], the authors introduce a mathematical framework for analyzing metamorphic systems based on embedding the state space—the space of all possible states of a given metamorphic system—into a continuous space. This embedding, called the state complex is well suited to a recent consensus algorithm [10] that relies on pairwise midpoint computations. Indeed, the state complex can be equipped with an adequate metric, so as to yield a CAT(0) metric space. Hence, the main contribution of this paper is to propose a distributed consensus algorithm that provably converges and is well adapted to the state space of metamorphic systems.
The paper is organized as follows. The first section details the mathematical background underpinning the metamorphic systems state space embedding, as well as gives a formal description of the consensus problem. The second section exposes the random pairwise midpoint algorithm. Section 3 explains how to compute the midpoint of any two points in a cubical complex. Finally, Section 4 provides numerical simulations for the proposed consensus algorithm.
2. Framework
2.1. Metamorphic Systems: Definition and Examples
There are many examples of metamorphic/reconfigurable systems, such as reconfigurable manufacturing systems [1] and phylogenetic trees [2]. Another example, one in which we will be more interested in this paper, is that of metamorphic robots, which were described by Østergaard et al. in [11] as robotic systems:
- That consist of several identical and physically independent unit modules;
- For which its modules can be connected to each other in many possible ways in order to form rigid structures;
- For which its modules can disconnect and reconnect while the system is active;
- For which it can change the way its modules are connected, i.e., it is fully automatic.
Some of these robots are lattice-based, meaning that the robotic modules occupy a discrete set of possible positions, this set of possible positions forming a lattice. The nature of the lattice depends on the geometry of the modules: it can be hexagonal, squared, dodecahedral, etc. These metamorphic systems can be mathematically described as a collection of states on a graph (see Appendix A).
Representing the various states of a metamorphic system by their lattice configuration will prove to be insufficient for finding a simple consensus protocol. Indeed, the lattice representation does not provide an ordering of states. Following [8], we represent a system configuration as a point in a cubical complex
, called the state complex (see, also, Appendix B for a definition). The zero-dimensional skeleton of this complex is the set of states, and two vertices are linked by an edge if their corresponding states differ by a single action of a generator (see Appendix A). A k-cube of the complex represents k commutative movements, i.e., movements that are non-overlapping whatever their order (see [8] for a rigorous definition).
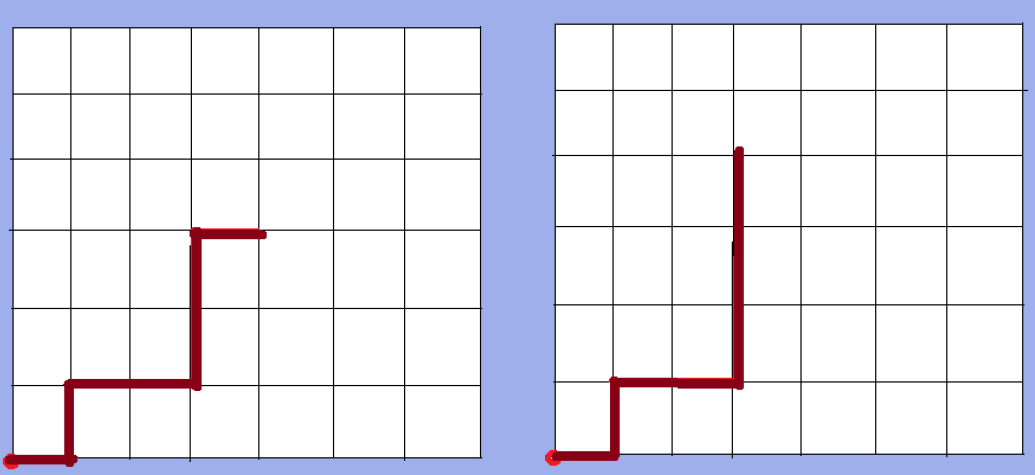
An example of a metamorphic system is the robotic arm, which consists of attached links, inside a grid with one of its extremities attached to the base point (0, 0) of the grid (see Figure 1).
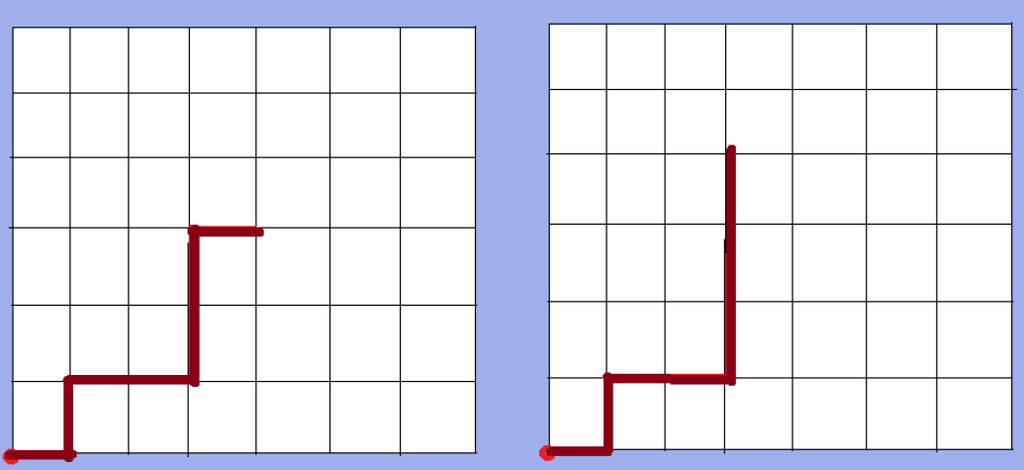
Figure 1.
Example of a lattice-based reconfigurable system: the robotic arm. The edges in color indicate the presence of a unit module; a black edge indicates its absence. The arm is attached at its base point (0, 0). Here, an elementary movement has been performed by the module at the end of the arm, which changes the overall form of the system.
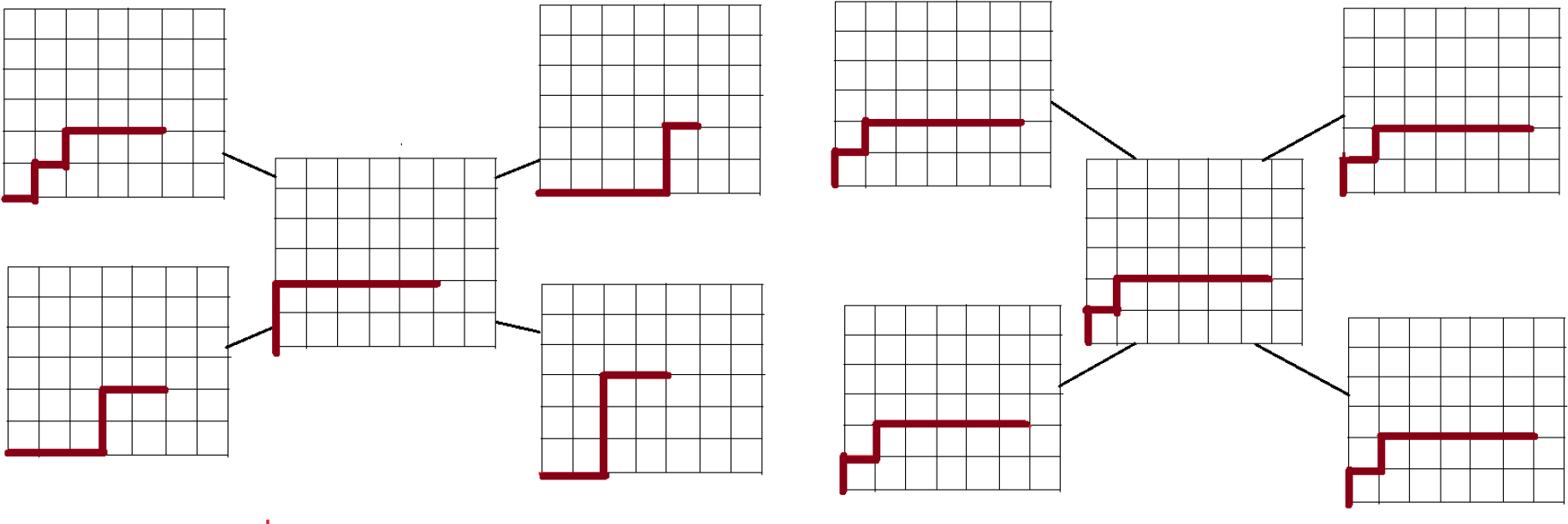
We assume in this work that the metamorphic systems form a network; two systems are connected whenever they are able to communicate with each other. The aim is to synchronize all of the systems that compose the network, i.e., all of the systems should have the same configuration, as shown in the example of Figure 2.
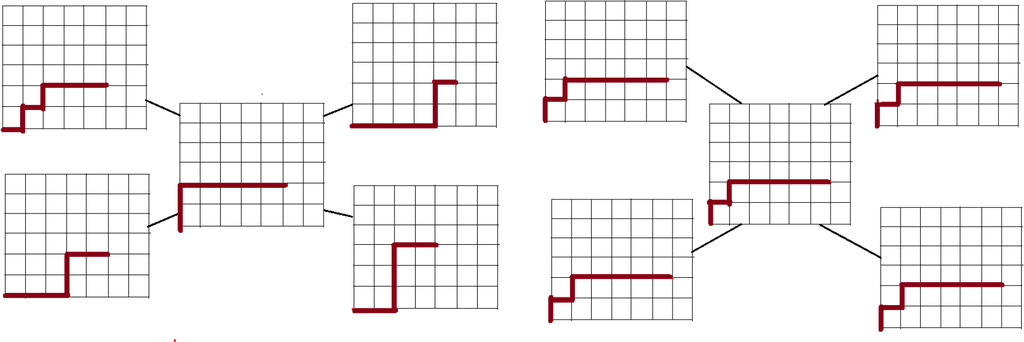
Figure 2.
In this example, we are given five robotic arms. In the leftmost figure (describing the initial state), each arm has its own configuration. The rightmost figure represents a consensus state, in which all of the arms share a common configuration.
Having described the model chosen for metamorphic systems, we next review the mathematical framework of the consensus problem.
2.2. Framework of the Consensus Problem
2.2.1. Network
Following the approach of [5], we model the network of metamorphic systems by a connected graph G = (V, E) with vertices V representing the metamorphic systems (agents) and whose edges E represent the communication links between these agents. We assume the graph to be undirected, which means that if an agent can communicate with another agent, then the converse is also true; this hypothesis is not too unrealistic if we suppose that all of the agents are identical and that the movement speed of the agents is very small compared to their communication speed. When a communication link exists between two agents, we say that the two agents are neighbors. We denote by
(v) the set of all neighbors of the agent v ∈ V.
As in [5], we assume that the time model is asynchronous, i.e., that each agent has its own Poisson clock that ticks with a common intensity λ (the clocks are identically made), and moreover, each clock is independent of the other clocks. When an agent clock ticks, the agent is able to perform some computations and wake up some neighboring agents. This time model has the same probability distribution as a global single clock ticking with intensity Nλ and selecting uniformly randomly a single agent at each tick. This equivalence is described, e.g., in [5]. Notice also that link e = {v, w} is not necessarily used by agents v and w at a given time: v or w might not be awakened.
2.3. Communication
At a given time k, we denote by Vk the agent whose clock ticked and by Wk the neighbor that was in turn awaken. Therefore, at time k, the only communicating agents in the whole network are Vk and Wk. A single link is then active at each time; hence, at a given time, most links are not used. We assume that (Vk, Wk) are independent and identically distributed and that the distribution of Vk is uniform over the network, while the distribution of Wk is uniform in the neighborhood of Vk. More precisely, the probability distribution of (Vk, Wk) is given by:
Notice that this probability is not symmetric in (v, w). It is going to turn out to be convenient to also consider directly the link {Vk, Wk}, forgetting which node was the first to wake up and which node was second. In this case,
is of course symmetric in (v, w). One has:
The communication framework considered here is standard [5].
2.3.1. Data Space
We assume that the cubical complex is equipped with the metric d induced from the Euclidean metric on each cube. The skeleton of the complex is a metric graph called the transition graph and is denoted.
Initially, each node v has an initial value xv(0), and X0 = (x1(0),…, xN(0)) is the tuple of initial values. A consensus state has the form X∞ = (x∞,…, x∞) with:
. We denote by xv(k) the value stored by the agent v ∈ V at time k and Xk = (x1(k),…, xN(k)) the global state of the system at that instant.
We want to apply a distributed algorithm in order to achieve the consensus state.
being a metric space, a candidate algorithm could be the average pairwise midpoint [10] algorithm. This algorithm requires
to be a CAT(0) metric space.
Definition 1. Let (M, d) be a metric space. A geodesic curve c in X is a map c : [0, l] → X from a closed interval I = [0, l] to X, such that, for all t.t′ ∈ I:
A metric space is said to be geodesic if and only if, for any two points x, y ∈ X, there exists a geodesic c : [0, l] → X, such that c(0) = x and c(l) = y.
Definition 2 (CAT(0) inequality). Assume (X, d) is a geodesic metric space (a metric space in which any two points can be related by a geodesic) and Δ = (c0, c1, c2) is a geodesic triangle with vertices p = c0(0), q = c1(0) and r = c2(0). Let denote a comparison triangle (a triangle with the same edge lengths as Δ) in the Euclidean space. Δ is said to satisfy the CAT(0) inequality if, for any x = c0(t) and y = c2(t′), one has:
where is the unique point of, such that, and on, such that.
A geodesic metric space is said to be locally CAT(0) if any geodesic triangle of sufficiently small perimeter verifies the CAT(0) inequality. It is said to be globally CAT(0) if any geodesic triangle verifies the CAT(0) inequality.
For a thorough introduction to the subject, see [12,13].
Any state complex can be shown to be a locally CAT(0) space [14]. The global CAT(0) proprietyrequires an additional constraint on the state complex. In [14], a combinatorial criterion based on the notion of posets with inconsistent pairs is provided to verify whether a state complex is globally CAT(0).
Assumption 1. We shall make the fundamental assumption that the state complex of any metamorphic system involved in this paper is globally CAT(0). This assumption, while restrictive, still covers many interesting examples, like the robotic arm [3], phylogenetic trees [2], the hexagonal system [8], etc.
The following proposition links the existence and uniqueness of geodesics and midpoints with the CAT(0) property:
Proposition 1. If x and y are two points in a globally CAT(0) space X, then there is but one geodesic γ : [0, 1] → X, such that γ(0) = x and γ(1) = y, which we will denote from now on as [x, y]. The midpoint of x and y is defined as and is always well defined and unique.
Now that the working framework is set (connected and undirected communications graph, Poisson clocks, data space, etc.), we will propose in the next section a consensus algorithm based on the gossip protocol [5] adapted to CAT(0) metric spaces.
3. Algorithm
3.1. Description
In this section, we expose a distributed algorithm that relies on distributed midpoint computation in
to drive a system of identical metamorphic systems into a consensus configuration—the random pairwise midpoint algorithm [10]—which works as follows: At each count of the virtual global clock, one node v is selected uniformly randomly from the set of agents V. The node v then randomly selects a node w from the neighbors of v in the communications graph. Both node v and w then compute and update their value to
.
This algorithm is well defined, since for any couple of points
, their midpoint exists and is unique. This is due to the fact that
is a globally CAT(0) space.

Algorithm 1.
Random Pairwise Midpoint.
| Input: a graph G = (V, E) and the initial nodes configuration Xv(0), v ∈ V for all k > 0 do |
| At instant k, uniformly randomly choose a node Vk from V and a node Wk uniformly randomly from . |
| Update: |
| Xv (k) = Xv (k − 1) for v ∉ {Vk,Wk} |
| end for |
This algorithm belongs to the class of consensus protocols, which has been shown to achieve convergence towards a consensus state in [15]; the convergence rate is established as linear in [10]. This assumes, however, that it is possible to compute the midpoint of any two points with reasonable complexity. While there is no closed expression for the midpoint of any two points in
, there is a procedure described in the next section that permits the computation of the midpoint.
4. Computing the Midpoint
In [16], an algorithm is given for computing means and medians in general CAT(0) metric spaces; we are here interested in finding the midpoint
of any two given points x and y of a CAT(0) cubical complex
, so we first determine the geodesic [x, y] between x and y.
Let x = (x1 … xN) and y = (y1 … yN) be the coordinates of x and y in the current standard embedding of
in
(see Appendix C for an exposition of the standard embedding).
Then, we define v = (v1,…, vN) and w = (w1,…, wN), such that for i ∈ {1,…, N}:
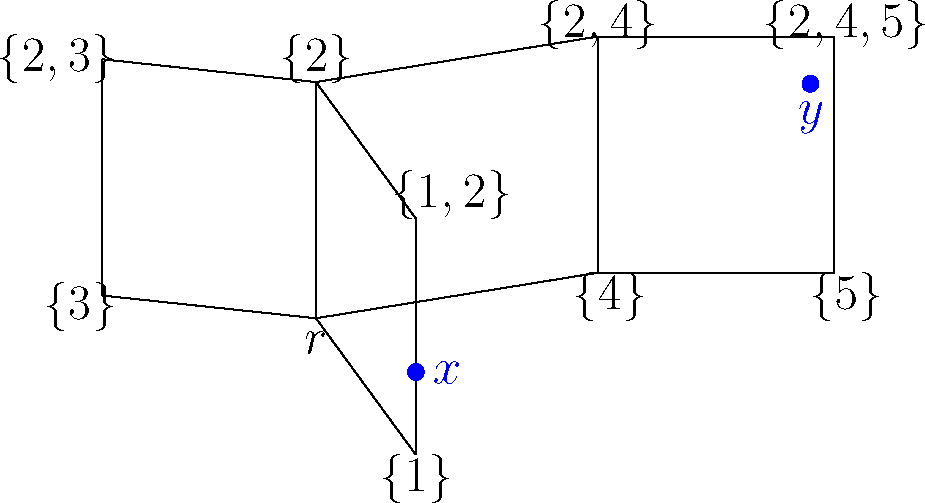
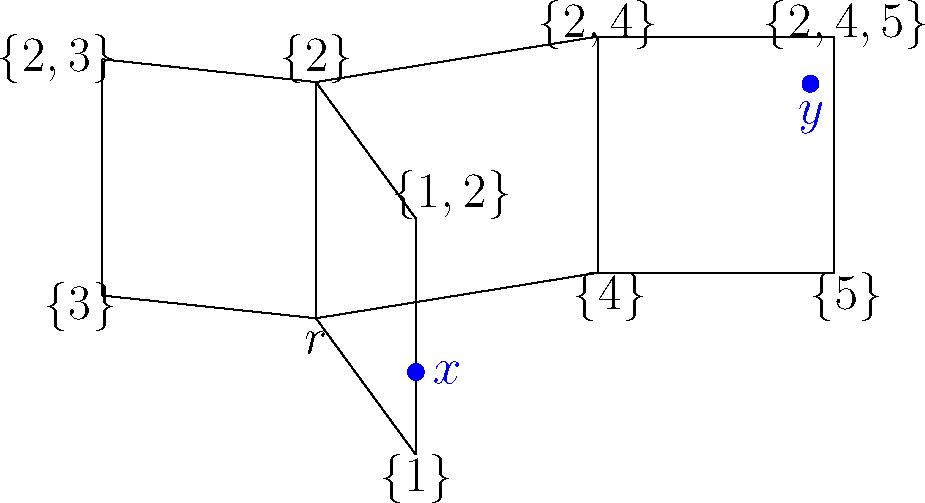
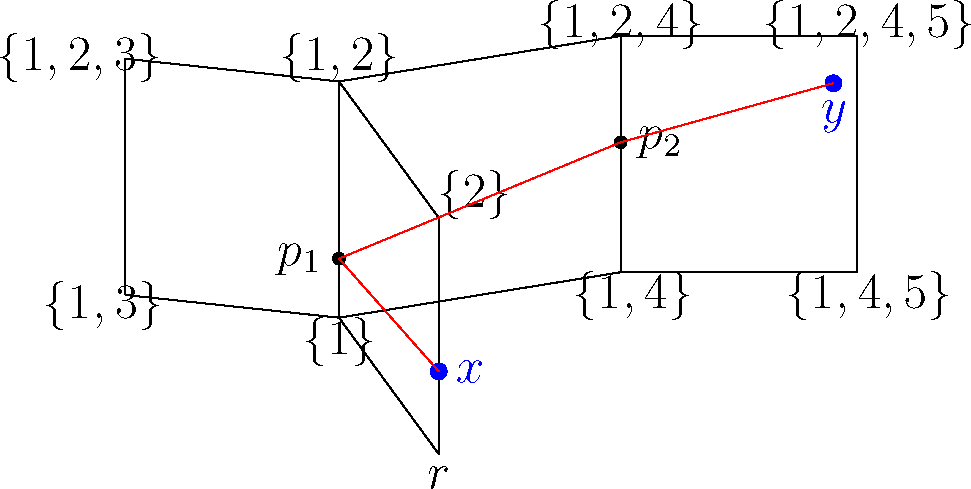
Figure 3.
Example of a cubical complex with an initial root vertex r. We want the geodesic between the points x = (1, 0.25, 0, 0, 0) and y = (0, 0.75, 0, 1, 0.75).
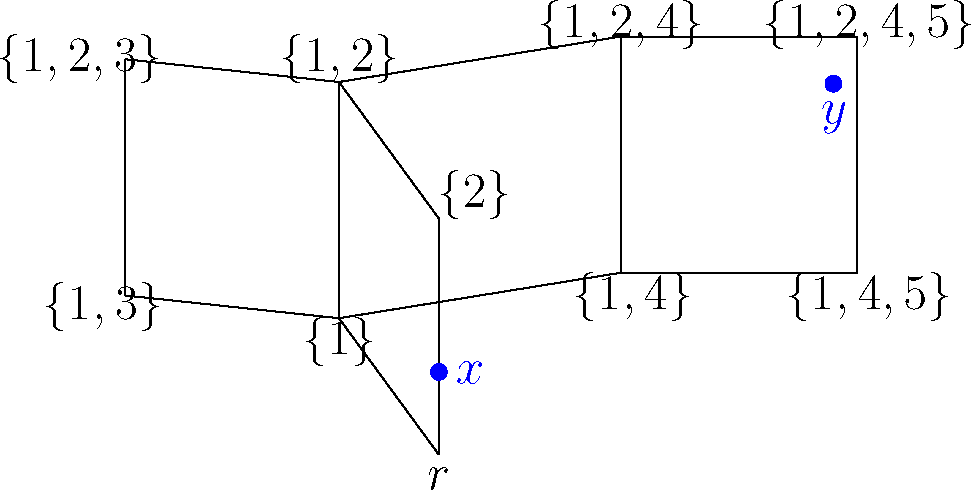
Next, we re-root the cubical complex at v and change the labeling of its vertices consequently, as well as the coordinates of x and y. To obtain the new coordinates of any point a = (a1,…, aN) in the new standard embedding, we update: ai,new = 1 − ai,old if vi = 1 and ai,new = ai,old if vi = 0 (see Figures 3 and 4).
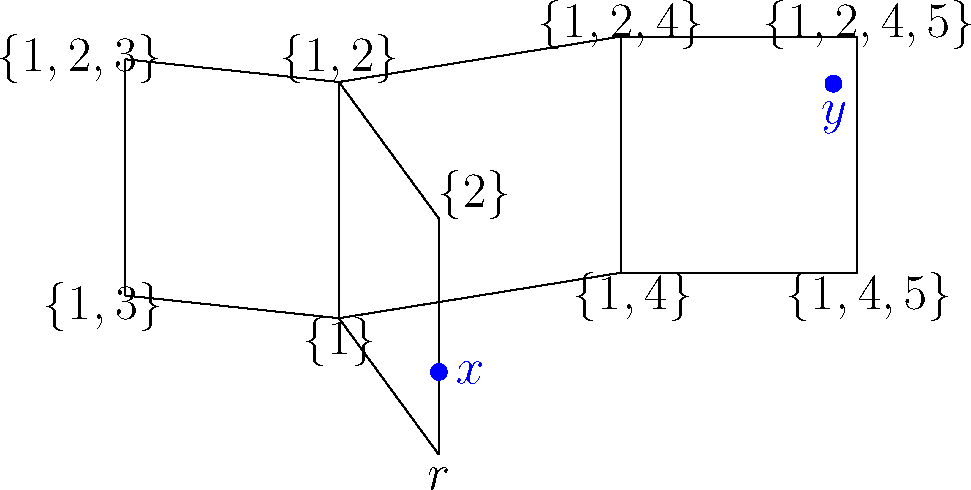
Figure 4.
We re-root the cubical complex at v, and the new coordinates are: x = (0, 0.25, 0, 0, 0) and y = (1, 0.75, 0, 1, 0.75). The coordinates of w are (0, 1, 0, 1, 1).
We denote by Iw = {i ∈ {1,…N}|wi = 1}, the order ideal associated with the vertex w. Now that the complex is re-rooted, we need to find the cubical sequence that contains the geodesic between x and y. According to [14], a valid sequence (Ck)1≤k≤n = (Ik, Mk)1≤k≤n of cubes containing the geodesic, consists of a sequence of order ideals I1 ⊂ I2 ⊂ ⋯ ⊂ In = Iw and maximal antichains Mk ⊂ Ik, 1 ≤ k ≤ n (see Appendix B for the representation of individual cubes of a complex). To find this sequence, we take the subset of minimal elements of Iw and I1, and set M1 = I1. Then, in order to form Ck = (Ik, Mk) from Ck−1 = (Ik−1, Mk−1), we take the subset of minimal elements mk of Q−Ik−1, put Ik = Ik−1 ∪ mk and let Mk be the maximal antichain of Ik. Using this procedure until Ik = P, we obtain a valid cube sequence, which contains the geodesic. In the example of Figures 3 and 4, we have: I1 = {2, 3}, M1 = {2, 3} and I2 = {2, 3, 4}, M2 = {2}.
After the cube sequence has been determined, we then have to find the ‘breakpoints’ from which the geodesic passes. The points {p1,…, pn−1} are such that: ‖x − p1‖ + ‖p1 − p2‖ + ⋯ + ‖pn−1 − pn‖ + ‖pn − y‖ is minimal and that for each k ∈ {1,…, n − 1} pk ∈ Fk with Fk being the common frontier of (Ik, Mk) and (Ik+1, Mk+1), which is the cubical cell (Ik, Mk ∩ Mk+1). This problem can be cast as a touring problem with n polyhedral regions and 2n facets [14].
The touring problem is a second order cone optimization problem, for which numerical solvers exist. We solve the touring problem and obtain a series of points p1…pn and the distances t1…tn−1 between pk and pk+1 (see Figure 5).
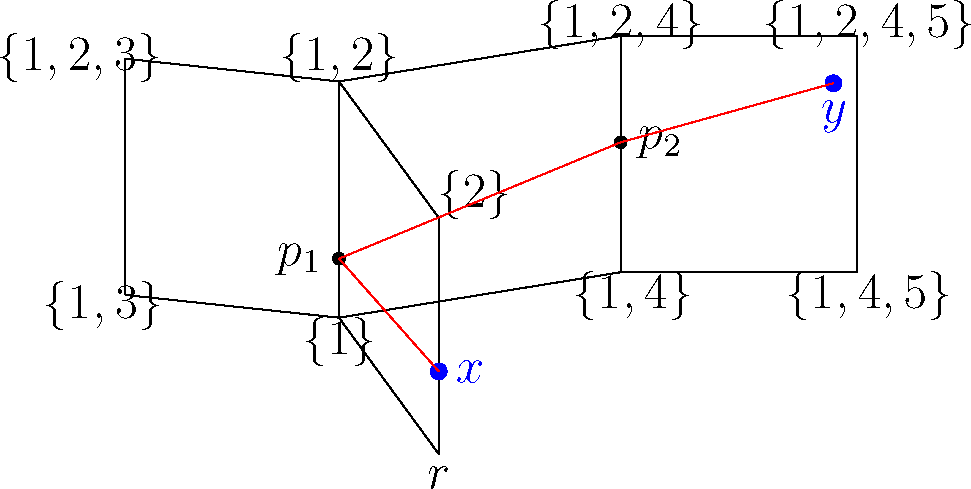
Figure 5.
In this example, the cube complex and the points x and y are such that we have a non-co-linear sequence of points {p1, p2} that the geodesic between x and y (drawn in red) passes through. The cube sequence {C1, C2, C3} contains this geodesic.
Knowing the sequence of points (pi)1≤i≤n and distances (ti)0≤i≤n, we want to determine the midpoint of x and y; we have two cases:
Case 1: n > 0.
First, we determine the cubical cell of (Ck)1≤k≤n+1 that contains the midpoint. Let
; then, we have:
and
. Using the convention p0 = x and pn+1 = y, the analytic expression of
is:
with:
- .
- .
- .
Case 2: n = 0.
In this case, x and y belong to the same cubical cell, and we have:
.
5. Numerical Results
In this section, we apply the previously described algorithm to two examples of a lattice-based metamorphic systems, the robotic arm, and the hexagonal lattice robot.
To understand why the robotic arm is CAT(0), one must construct a poset with inconsistent pairs associated with the state complex of the arm (see Appendix B.2).
Definition 3. Define for any robotic arm with n articulations Rn the set Pn = {(x, y)|y ≥ 0, y ≤ x, x ≤ n − 1}, and define the partial order relation ≤, such that (x1, y1) ≤ (x2, y2) if and only if x1 ≤ x2 and y1 ≤ y2.
Using the partially ordered set Pn, we can show that the state complex of Rn is CAT(0) through the following proposition:
Proposition 2. [3] Let be the cubical complex of Rn rooted at the state where the arm is completely horizontal.
Then, there is a bijection between the possible states of Rn and the order ideals of Pn.
We analyze the convergence of the pairwise midpoint algorithm using as a criterion the variance function:
Definition 4. Given a configuration, the variance function is defined as:
where d is the distance between two points in
If σ2(x) = 0, then x1 = x2 ⋯ = xN, and we have achieved a consensus state. In [10], it is proven that for a sequence of points X(k) = (x1(k),…, xN(k)) generated according to the pairwise midpoint algorithm, the function σ2 converges to zero at a linear rate.
Theorem 1. Let Xk = (x1(k),…, xN(k)) denote the sequence of random variables generated by Algorithm 1; then, there exists L < 0, such that,
In order to randomly sample a set of initial coordinates, we begin by assigning to each metamorphic system a vector (x1,…, xN), where each xi is sampled randomly and uniformly from the interval [0, 1]. Then, we do the following: we check if there exists i, j, such that i ≺ j and xj ≠ 0; if so, then set xi = 1 (the ≺ relation being the partial order of the poset associated with the cubical complex
in its initial rooting).
5.1. Results for the Robotic Arm
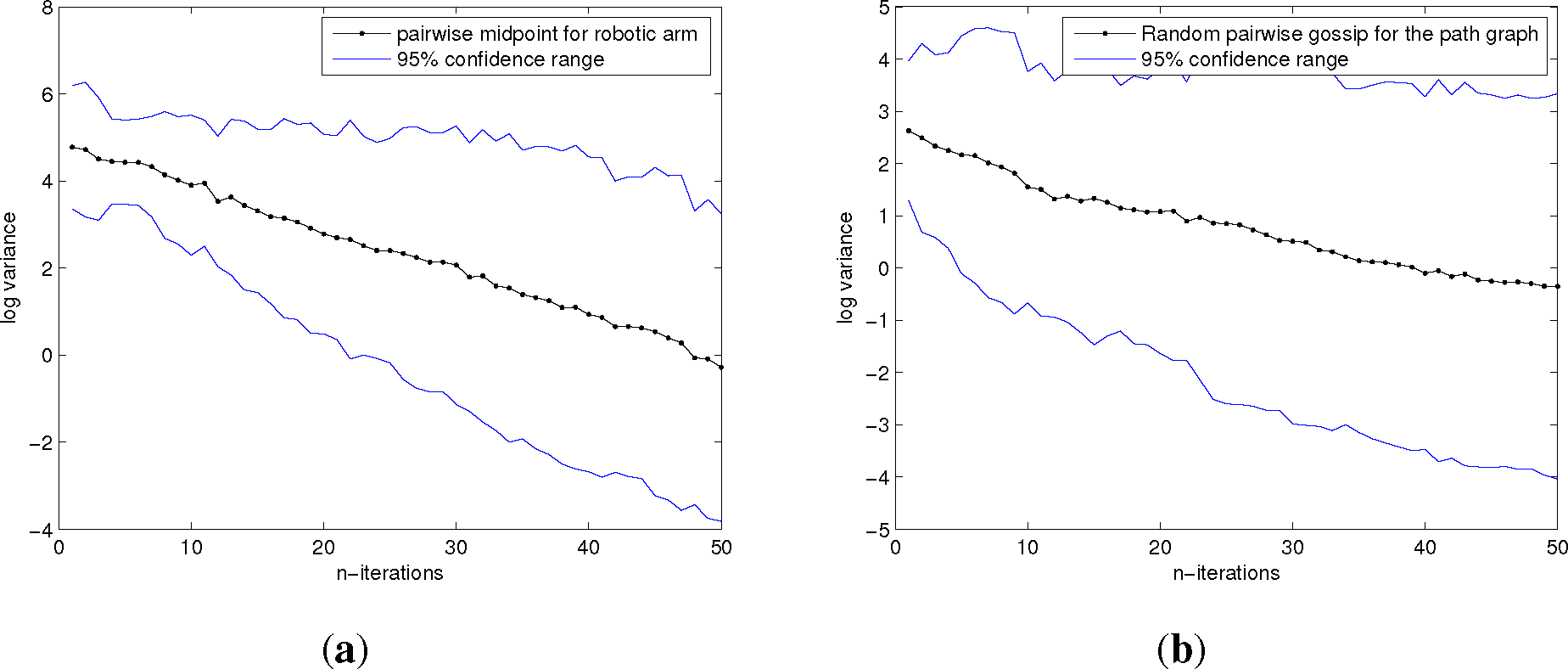
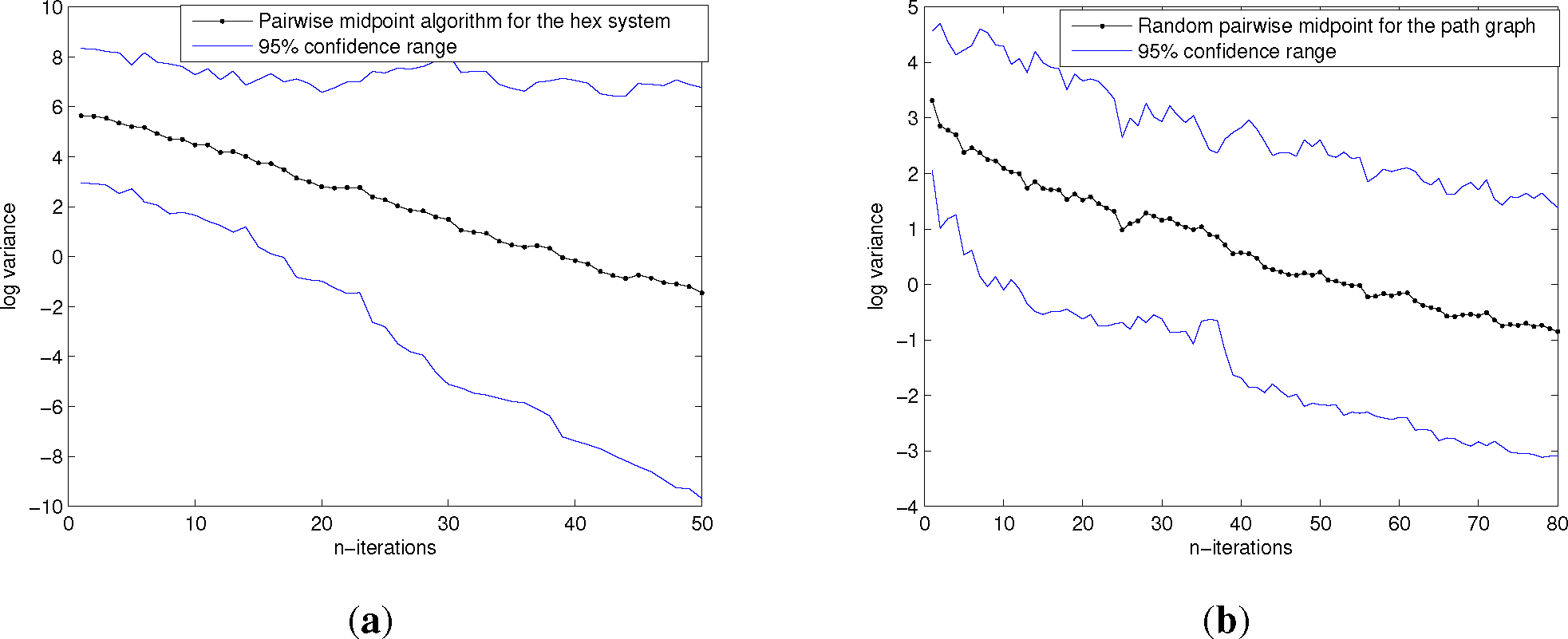
We plot the log-variance log σ2 as a function of the number of iterations k, for a complete graph of 10 robotic arms of n = 7 joints (see Figure 6), then for a path graph of 10 robotic arms of the same type. In both cases, we observe in Figure 7 a linear curve with a negative slope in accordance with the results of [10]. In the case of the path graph, however, the slope is smaller than for the complete graph.
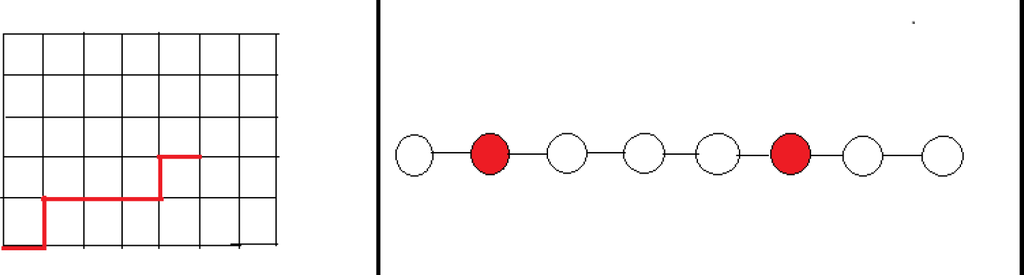
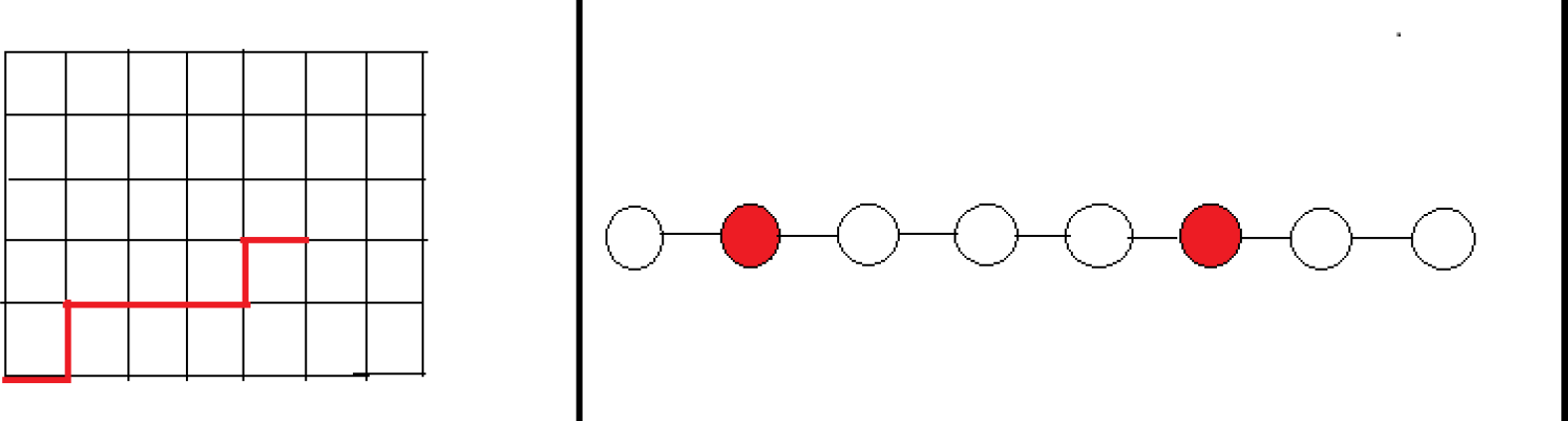
Figure 6.
On the right, a robotic arm with n = 7 articulations and the associated state graph.
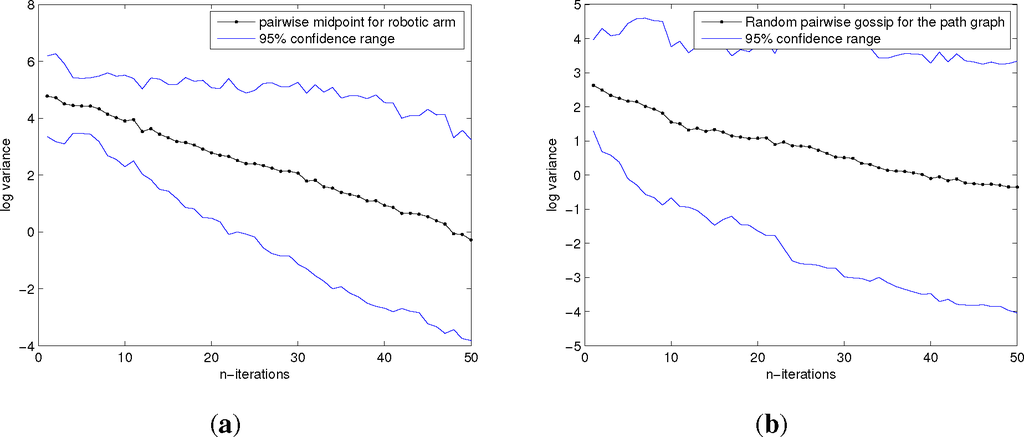
Figure 7.
Plot of n → log σ2 for a network of k = 10 robotic arms with n = 7 articulations. (a) The underlying communications graph is the complete graph, while on (b), it is the path graph. Because of the stochastic nature of the algorithm, the procedure is averaged over 30 runs. The resulting curve is a line of a negative slope of bigger magnitude for the complete graph than for the path graph.
5.2. Results for the Planar Hexagonal Lattice
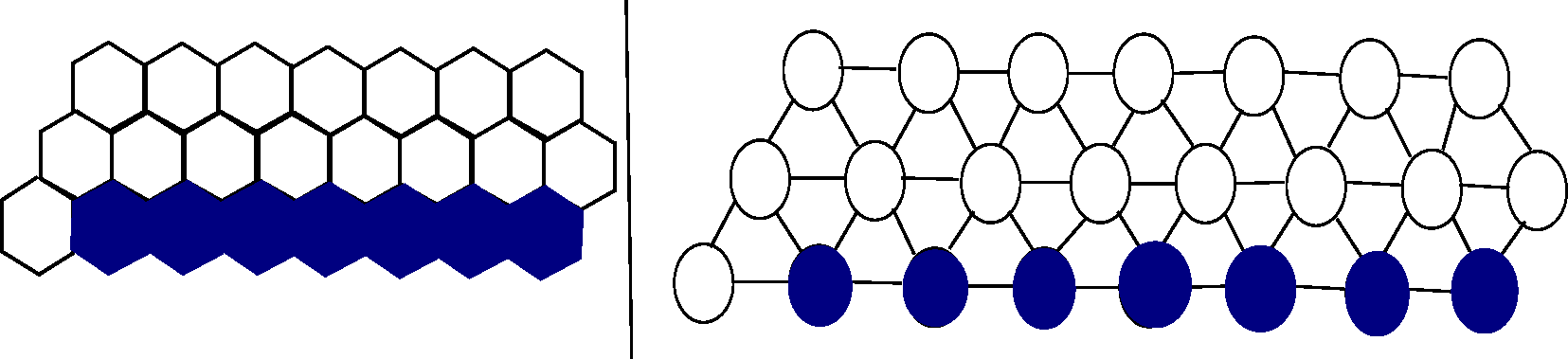
The same analysis is applied to the hexagonal lattice system [8], which is a connected aggregate of hexagonally-shaped modules that occupy a planar lattice. Its graph representation and associated cubical complex can be seen in Figure 8.
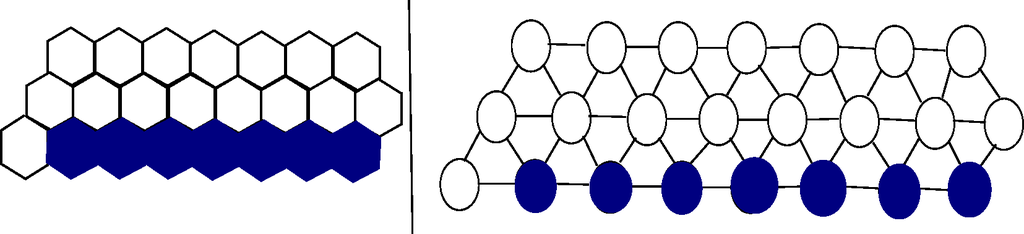
Figure 8.
On the right, a hexagonal lattice system and its associated state graph.
We observe similar patterns as for the robotic arms experiment; in Figure 9 the function log σ2 decreases at a linear rate for both the complete graph and the path graph cases.
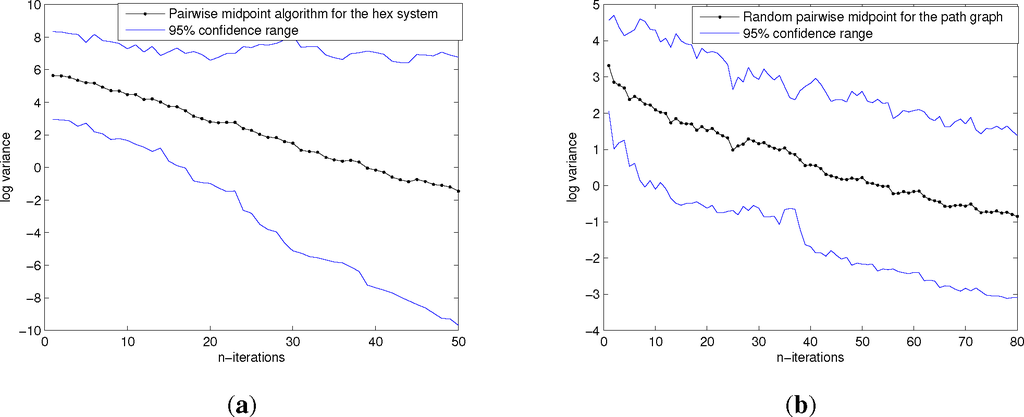
Figure 9.
Plot of n → log σ2 for a network of k = 10 hexagonal systems. (a) The underlying communications graph is the complete graph, while on (b), it is the path graph. Because of the stochastic nature of the algorithm, the procedure is averaged over 30 runs. The resulting curve is a line of a negative slope of bigger magnitude for the complete graph than for the path graph.
6. Conclusions
The random pairwise midpoint algorithm can be successfully applied to discrete combinatorial systems, like the case of metamorphic systems. This is a non-trivial example of a purely metric application of this algorithm, whose exponential convergence towards a consensus state has been confirmed through numerical experiments on two examples of metamorphic systems. The same method could be applied to the space of phylogenetic trees. Another application could be that of distributed optimization, where N identical metamorphic systems, each with its own utility function
, try to minimize a collective objective function
; the underlying communication network has no fusion node.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
A. Modeling Metamorphic Systems
For a rigorous definition of metamorphic systems, we follow the approach of [8]. We represent the lattice by its dual graph
, whose vertices represent the individual cells of the lattice; two vertices are joined by an edge if and only if their corresponding cells are adjacent in the lattice. We associate with this graph a set of labels
on the set of vertices to indicate whether the corresponding cell is occupied or not and, in the former case, whether it is occupied by an obstacle or by a module and of which type. A state of the system is any map
. The metamorphic system dynamically changes its state through a set of elementary movements that satisfy the following rules: (i) units cannot overlap during reconfiguration; and (ii) overall connectivity should always be maintained. This is done via generators, which are defined below:
Definition 5. [9] Let be a graph and a set of labels. A generator ϕ is a collection of three objects:
- A support, which is a subgraph of;
- A trace, , which is a subgraph of SUP(ϕ);
- An non-ordered pair of states u0, u1 : , verifying:
where are the vertices of SUP(ϕ).
The support of the generator corresponds to the region of the graph that contains the necessary information to verify whether the movement is feasible (i.e., the absence of obstacles, no modules overlapping and the connectivity of the system is maintained). The trace of the generator is the region of the graph where the movement actually takes place.
Definition 6. [9] A generator is said to be admissible at a state U if:. The action of ϕ, denoted Φ, maps a state u :
to a new one Φ[u] :
, given by:
Thus, a generator ϕ acts on a state U by modifying its restriction on the vertices of TR(ϕ) from u0 to u1. This corresponds to an elementary movement of unit modules. However, a metamorphic system should be able to perform many such elementary movements simultaneously; in order for that to be feasible, the movements have to be compatible, i.e., their simultaneous execution does not lead to module overlap or loss of system connectivity. For that, we introduce the following definition:
Definition 7. [9] In a metamorphic system, a collection of generators {ϕi} is said to be commutative if:
B. The State Complex
B.1. Definition
A cubical complex can be seen as a collection of cubes glued together using isometries.
Definition 8. [17] (p.112) Let Γ ⊂ ℕ and (Ci)i∈Γ be a collection of Euclidean unit cubes of various dimensions. Additionally, letbe a disjoint union of these cubes. A cubical complex is the quotient of X by an equivalence relation ~, such that if p : X →
is the natural projection, then:
- For every i ∈ Γ, the restriction pi of p to the cube Ci is injective.
- If pi(Ci) ∩ pj(Cj) ≠ Ø, then there is an isometry hi,j from a face Ti ⊂ Ci onto a face Tj ⊂ Cj, such that pi(x) = pj(x′) if and only if x′ = hi,j(x).
Definition 9. [9] The state complex of a metamorphic system is a cubical complex. Each k-cube e(k) of is an equivalence class, where:
- is a k-upletof commuting generators.
- u is a state for which the generators are admissible.
- if and only if ∃σ ∈ tk, such that: ∀i ∈ {1,…, k}; we have:; and u0 = u1 on the subgraph:.
The boundary of each k-cube is a collection of 2k faces:
One advantage of using the cubical complex representation over that of the transition graph is that it shows which elementary movements can be performed simultaneously; and, thus, contains more information than the transition graph. It is not generally computationally feasible to construct the cubical complex associated with a given reconfigurable system, but there are some interesting cases where it is possible to do so, like the case of the robotic arm [3].
B.2. Encoding as a Partially-Ordered Set
Given a cubical complex
and a vertex v (called the root vertex) of
, one can introduce a partial order relation in the set of vertices of
by stating that a u ≺ w if and only if there is an edge path geodesic (i.e., a geodesic on the metric graph associated with
) from the root v to w that passes through u. The complex
can thus be seen as a partially-ordered set. In [14], it is shown that if one can choose the special node v, such that the set of vertices of
equipped with the partial order relation ≺ is a poset with inconsistent pairs, then
is a globally CAT (0) cubical complex. This last propriety guarantees the existence and uniqueness of the midpoint of any given two points and allows us to apply the random midpoint algorithm on a network of agents whose data are encoded in a cubical complex. We assume in this paper that all of the studied complexes are CAT (0).
Reciprocally, given a poset with inconsistent pairs (P, ≺), one can build a lattice whose summits are the order ideals of (P, ≺) that do not contain any inconsistent pairs (such order ideals are said to be consistent). An edge is drawn between two summits if their corresponding ideals differ by exactly one element. The vertices are ordered according to their corresponding ideals, u < w if and only if the order ideal Iu corresponding to the vertex u is a subset of Iw, the order ideal associated with the vertex w (u < w ⇔ Iu ⊂ Iw), as shown in Figure B1.
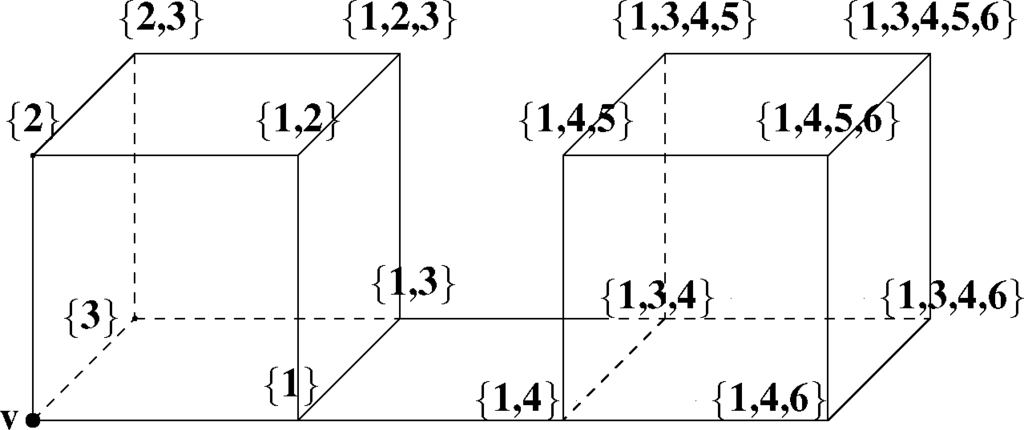
Figure B1.
The cubical complex associated with the poset (P = {1, 2, 3, 4, 5, 6}, ≺), such that: 1 ≺ 4, 1 ≺ 5 and 4 ≺ 6. Each vertex is labeled by a consistent order ideal of P.
Figure B1.
The cubical complex associated with the poset (P = {1, 2, 3, 4, 5, 6}, ≺), such that: 1 ≺ 4, 1 ≺ 5 and 4 ≺ 6. Each vertex is labeled by a consistent order ideal of P.
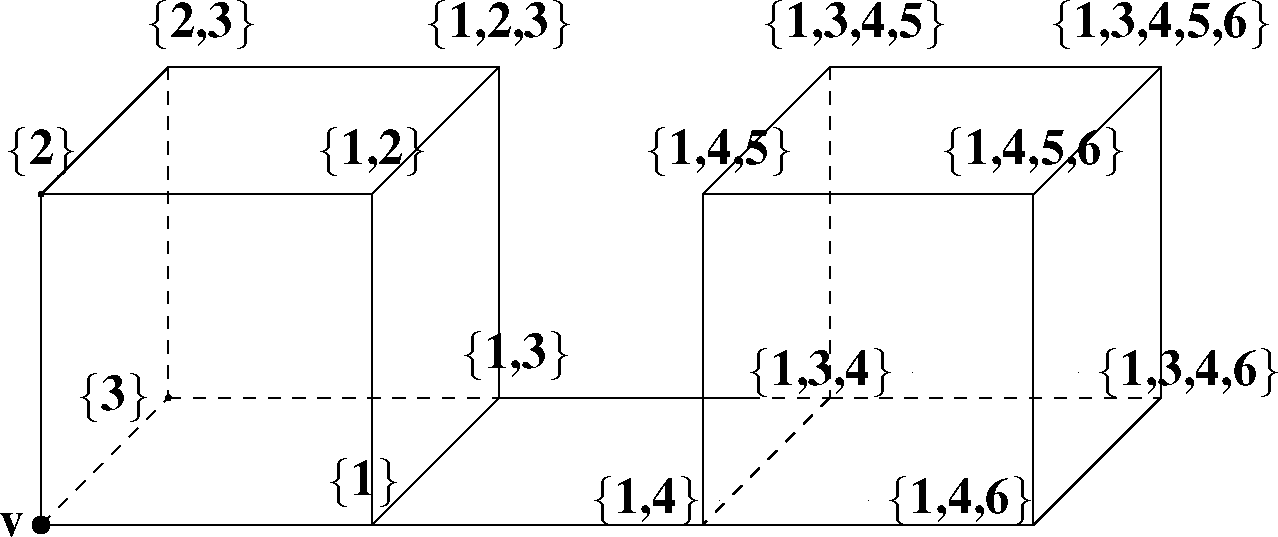
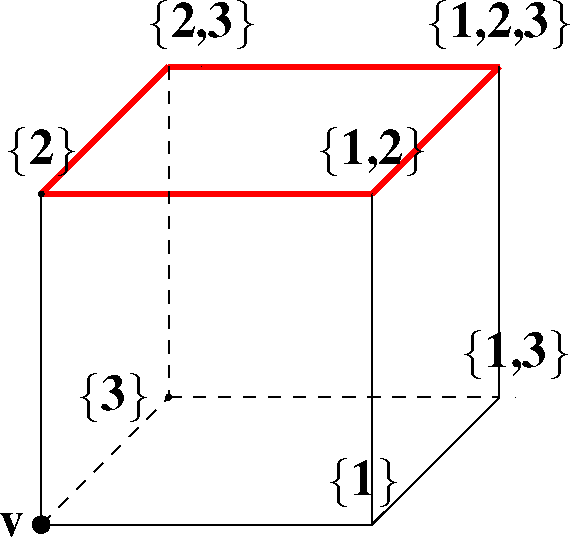
Individual cubes are represented by a pair (I, M), with I a consistent order ideal and M a subset of the maximal element of I; such a cube is of dimension |M|, and its vertices are found by removing from I all of the possible subsets of M (Figure B2 gives an example).
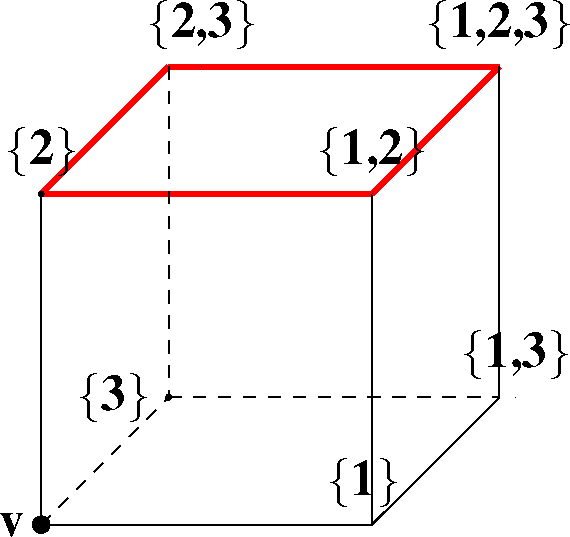
Figure B2.
In this example, the 2-dimensional cube highlighted in color is represented by the pair (I, M) with I = {1, 2, 3} and M = {1, 3}.
Figure B2.
In this example, the 2-dimensional cube highlighted in color is represented by the pair (I, M) with I = {1, 2, 3} and M = {1, 3}.
C. The Standard Embedding
One way to embed the cubical complex associated with a poset with inconsistent pairs of cardinal N is the so-called standard embedding [14]. An element u ∈
is represented by an N-tuple u = (u1,…, uN), where ∀i ui ∈ [0, 1], and if for some (i, j) ∈ {1,…, N}2, we have uj ≠ 0 and uj > ui, then we must have ui = 1. Furthermore, if xi and xj are inconsistent, then: uiuj = 0.
Figure 3 shows an example of a cubical complex where the standard embedding coordinates of the points x and y are: x = (1; 0.25; 0.25; 0) and y = (1; 0.75; 1; 0.75).
References
- Koren, Y.; Heisel, U.; Jovane, F.; Moriwaki, T.; Pritschow, G.; Ulsoy, G.; van Brussel, H. Reconfigurable Manufacturing Systems. In Manufacturing Technologies for Machines of the Future; Dashchenko, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2003; Part IV, Chapter 19; pp. 627–665. [Google Scholar]
- Billera, L.J.; Holmes, S.P.; Vogtmann, K. Geometry of the space of phylogenetic trees. Adv. Appl. Math. 2001, 27, 733–767. [Google Scholar]
- Ardila, F.; Baker, T.; Yatchak, R. Moving Robots Efficiently Using the Combinatorics of CAT(0) Cubical Complexes, 2012; arXiv preprint arXiv:1211.1442.
- Tsitsiklis, J. Problems in Decentralized Decision Making and Computation. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1984. [Google Scholar]
- Boyd, S.; Ghosh, A.; Prabhakar, B.; Shah, D. Randomized gossip algorithms. IEEE Trans. Inf. Theory. 2006, 52, 2508–2530. [Google Scholar]
- DeGroot, M.H. Reaching a consensus. J. Am. Stat. Assoc. 1974, 69, 118–121. [Google Scholar]
- Nejad, B.M.; Attia, S.A.; Raisch, J. Max-Consensus in a Max-Plus Algebraic Setting: The Case of Fixed Communication Topologies, Proceedings of the IEEE XXII International Symposium on Information, Communication and Automation Technologies (ICAT 2009), Sarajevo, Bosnia and Herzegovina, 29–31 October 2009; pp. 1–7.
- Abrams, A.; Ghrist, R. State complexes for metamorphic robots. Int. J. Robot. Res. 2004, 23, 811–826. [Google Scholar]
- Ghrist, R.; Peterson, V. The geometry and topology of reconfiguration. Adv. Appl. Math. 2007, 38, 302–323. [Google Scholar]
- Bellachehab, A.; Jakubowicz, J. Random Pairwise Gossip on CAT (κ) Metric Spaces, 2014; arXiv preprint arXiv:1405.4190.
- Østergaard, E.H.; Kassow, K.; Beck, R.; Lund, H.H. Design of the ATRON lattice-based self-reconfigurable robot. Auton. Robots. 2006, 21, 165–183. [Google Scholar]
- Bacak, M. Convex Analysis and Optimization in Hadamard Spaces; De Gruyter Series in Nolinear Analysis and Applications; De Gruyter: Genthiner Strasse 13, Berlin, Germany, 2014; Volume 22. [Google Scholar]
- Jost, J. Nonpositive Curvature: Geometric and Analytic Aspects; Lectures in Mathematics; ETH Zurich; Springer: Basel, Switzerland, 1997. [Google Scholar]
- Ardila, F.; Owen, M.; Sullivant, S. Geodesics in CAT (0) cubical complexes. Adv. Appl. Math. 2012, 48, 142–163. [Google Scholar]
- Grohs, P. Wolfowitz’s Theorem and Convergence of Consensus Algorithms in Hadamard Spaces; Technical Report SAM Report 2012-27; ETH: Zurich, Switzerland, 2012. [Google Scholar]
- Bacak, M. Computing medians and means in Hadamard spaces. SIAM J. Optim. 2014, 24, 1542–1566. [Google Scholar]
- Bridson, M.; Haefliger, A. Metric Spaces of Non-Positive Curvature; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).