New Exact Solutions of the New Hamiltonian Amplitude-Equation and Fokas Lenells Equation
Abstract
:1. Introduction
2. The Investigation of the New Hamiltonian Amplitude Equation
2.1. ETEM for the New Hamiltonian Amplitude Equation
2.2. Generalized Kudryashov Method for the New Hamiltonian Amplitude Equation
Case 1
Case 2
Case 3
Case 4
3. The Investigation of Fokas-Lenells Equation
3.1. ETEM for Fokas-Lenells Equation
3.2. GKM for Fokas-Lenells Equation
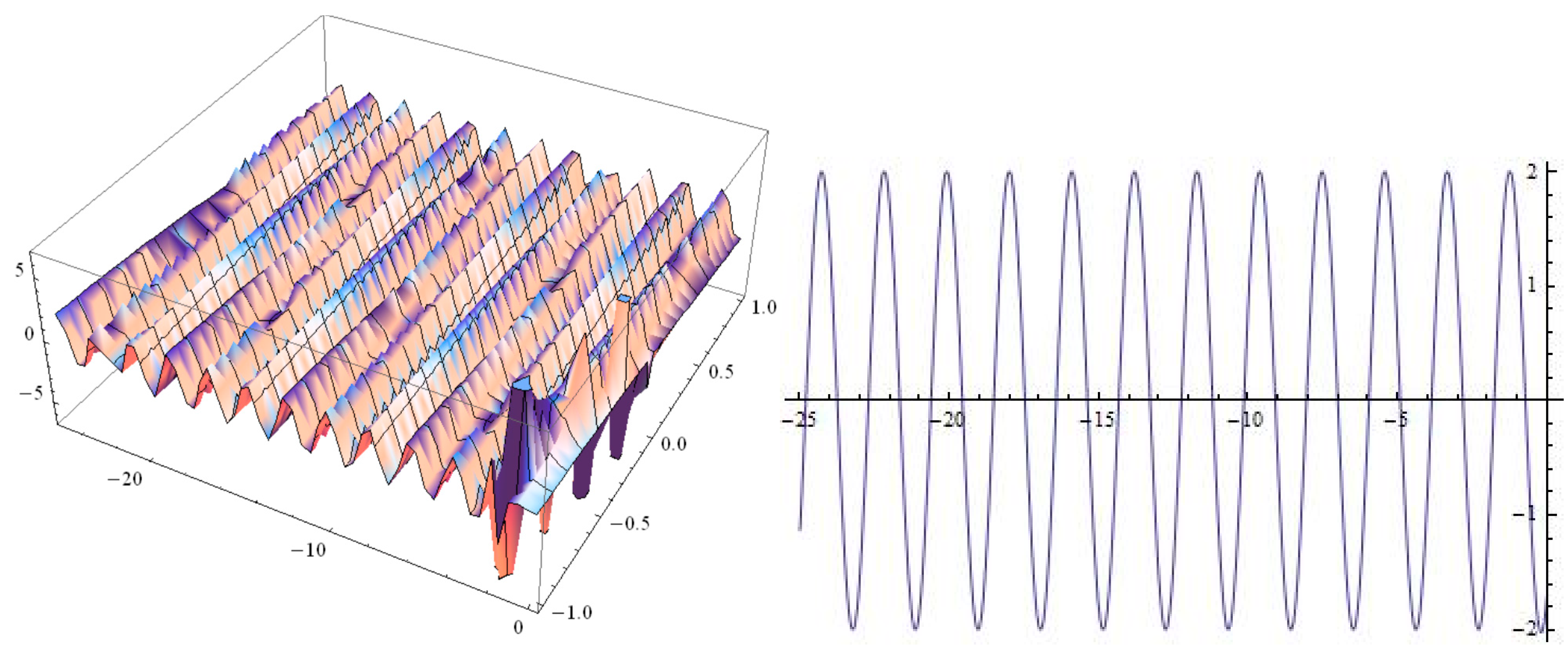




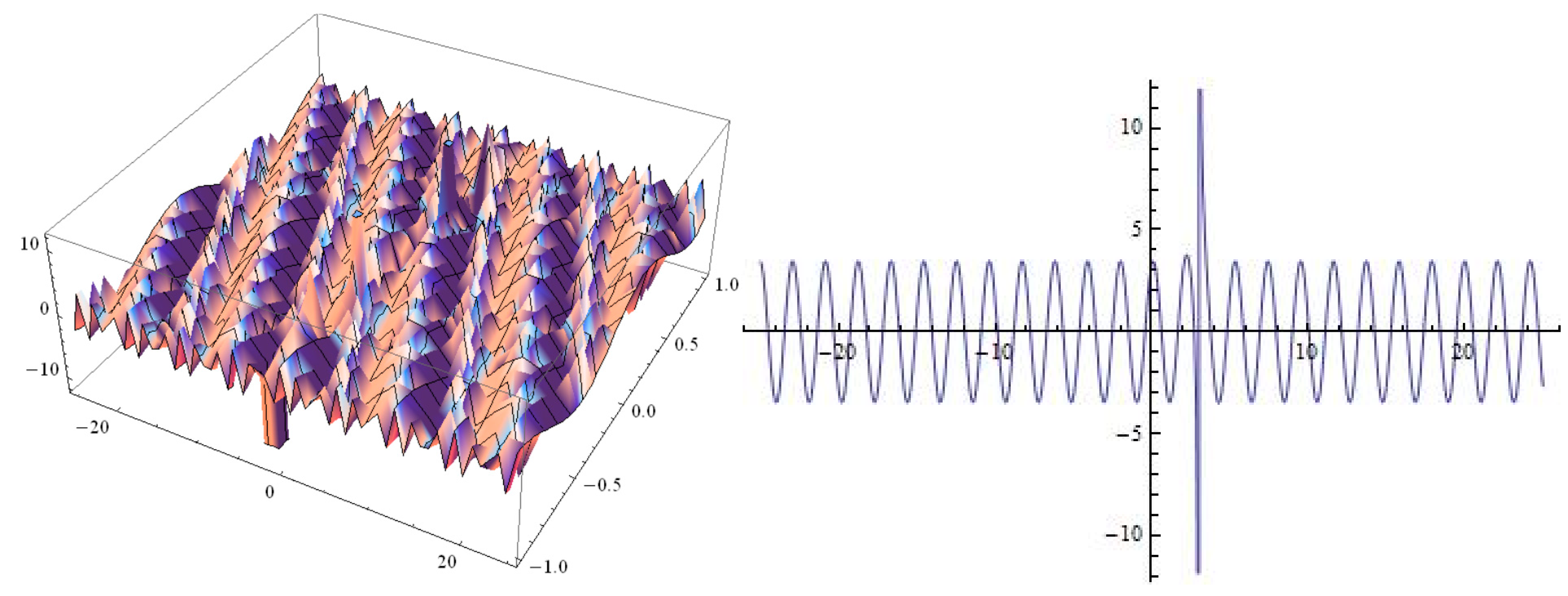




4. Conclusions
Author Contributions
Conflicts of Interest
References
- Xing, X. Physical Entropy, Information Entropy and Their Evolution Equations. Sci. China (Ser. A) 2001, 44, 1331–1339. [Google Scholar] [CrossRef]
- Carrillo, J. Entropy Solutions for Nonlinear Degenerate Problems. Arch. Ration. Mech. Anal. 1999, 147, 269–361. [Google Scholar] [CrossRef]
- Mascia, C.; Porretta, A.; Terracina, A. Nonhomogeneous Dirichlet Problems for Degenerate Parabolic-Hyperbolic Equations. Arch. Ration. Mech. Anal. 2002, 163, 87–124. [Google Scholar] [CrossRef]
- Karlsen, K.H.; Risebro, N.H. On the Uniqueness and Stability of Entropy Solutions of Nonlinear Degenerate Parabolic Equations with Rough Coefficients. Discret. Contin. Dyn. Syst. 2003, 9, 1081–1104. [Google Scholar] [CrossRef]
- Watanabe, H. Existence and Uniqueness of Entropy Solutions to Strongly Degenerate Parabolic Equations with Discontinuous Coefficients. Discret. Contin. Dyn. Syst. 2013, 2013, 781–790. [Google Scholar]
- Wang, M.; Li, X.; Zhang, J. The -Expansion Method and Travelling Wave Solutions of Nonlinear Evolution Equations in Mathematical Physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Ebadi, G.; Biswas, A. The Method and Topological Soliton Solution of the K(m,n) Equation. Commun. Nonlinear Sci. Numer. Simulat. 2011, 16, 2377–2382. [Google Scholar] [CrossRef]
- He, J.H.; Wu, X.H. Exp-function Method for Nonlinear Wave Equations Chaos. Soliton. Fract. 2006, 30, 700–708. [Google Scholar] [CrossRef]
- Fan, E. Extended Tanh-function Method and Its Applications to Nonlinear Equations. Phys. Lett. A 2000, 277, 212–218. [Google Scholar] [CrossRef]
- Tuluce Demiray, S.; Pandir, Y.; Bulut, H. Generalized Kudryashov Method for Time-Fractional Differential Equations. Abstr. Appl. Anal. 2014, 2014, 901540:1–901540:13. [Google Scholar] [CrossRef]
- Bulut, H.; Pandir, Y.; Tuluce Demiray, S. Exact Solutions of Time-Fractional KdV Equations by Using Generalized Kudryashov Method. Int. J. Modeling. Optim. 2014, 4, 315–320. [Google Scholar] [CrossRef]
- Tuluce Demiray, S.; Pandir, Y.; Bulut, H. The Investigation of Exact Solutions of Nonlinear Time-Fractional Klein-Gordon Equation by Using Generalized Kudryashov Method. AIP Conf. Proc. 2014, 1637, 283–289. [Google Scholar]
- Pandir, Y. Symmetric Fibonacci Function Solutions of Some Nonlinear Partial Differential Equations. Appl. Math. Inf. Sci. 2014, 8, 2237–2241. [Google Scholar] [CrossRef]
- Pandir, Y.; Gurefe, Y.; Kadak, U.; Misirli, E. Classification of Exact Solutions for Some Nonlinear Partial Differential Equations with Generalized Evolution. Abstr. Appl. Anal. 2012, 2012, 1–12. [Google Scholar] [CrossRef]
- Pandir, Y.; Gurefe, Y.; Misirli, E. Classification of Exact Solutions to the Generalized Kadomtsev–Petviashvili Equation. Phys. Scr. 2013, 87, 025003:1–025003:12. [Google Scholar] [CrossRef]
- Pandir, Y.; Gurefe, Y.; Misirli, E. The Extended Trial Equation Method for Some Time Fractional Differential Equations. Discret. Dyn. Nat. Soc. 2013, 2013, 491359:1–491359:13. [Google Scholar] [CrossRef]
- Pandir, Y.; Gurefe, Y. New Exact Solutions of the Generalized Fractional Zakharov-Kuznetsov Equations. Life Sci. J. 2013, 10, 2701–2705. [Google Scholar]
- Bulut, H. Classification of Exact Solutions for Generalized Form of K(m,n) Equation. Abstr. Appl. Anal. 2013, 2013, 1–11. [Google Scholar] [CrossRef]
- Bulut, H.; Pandir, Y.; Tuluce Demiray, S. Exact Solutions of Nonlinear Schrodinger’s Equation with Dual Power-Law Nonlinearity by Extended Trial Equation Method. Waves Random Complex Media 2014, 24, 439–451. [Google Scholar] [CrossRef]
- Pandir, Y. New Exact Solutions of the Generalized Zakharov–Kuznetsov Modified Equal-Width Equation. Pramana J. Phys. 2014, 82, 949–964. [Google Scholar] [CrossRef]
- Tuluce Demiray, S.; Bulut, H. Some Exact Solutions of Generalized Zakharov System. Waves Random Complex Media 2015, 25, 75–90. [Google Scholar] [CrossRef]
- Wadati, M.; Segur, H.; Ablowitz, M.J. A New Hamiltonian Amplitude Equation Governing Modulated Wave Instabilities. J. Phys. Soc. Jpn. 1992, 61, 1187–1193. [Google Scholar] [CrossRef]
- Teh, C.G.R.; Koo, W.K.; Lee, B.S. Jacobian Elliptic Wave Solutions for the Wadati–Segur–Ablowitz Equation. Int. J. Mod. Phys. B 1997, 11, 2849–2854. [Google Scholar] [CrossRef]
- Yomba, E. The General Projective Riccati Equations Method and Exact Solutions for a Class of Nonlinear Partial Differential Equations. Chin. J. Phys. 2005, 43, 991–1003. [Google Scholar]
- Krishnan, E.V.; Yan, Z.Y. Jacobian Elliptic Function Solutions Using Sinh-Gordon Equation Expansion Method. Int. J. Appl. Math. Mech. 2006, 2, 1–10. [Google Scholar]
- Feng, S.-Z.; Li, Y.-G.; Tian, L.-N.; Zhou, Y.-B. Periodic Wave Solutions for a New Hamiltonian Amplitude Equation. J. Lanzhou Univ. 2007, 43, 111–116. [Google Scholar]
- Taghizadeh, N.; Mirzazadeh, M. The First Integral Method to Some Complex Nonlinear Partial Differential Equations. J. Comput. Appl. Math. 2011, 235, 4871–4877. [Google Scholar] [CrossRef]
- Taghizadeh, N.; Najand, M. Exact Solutions of the New Hamiltonian Amplitude Equation by the -Expansion Method. Int. J. Appl. Math. Comput. 2012, 4, 390–395. [Google Scholar]
- Bekir, A.; San, S. The Functional Variable Method to Some Complex Nonlinear Evolution Equations. J. Modern Math. Front. 2012, 1, 5–9. [Google Scholar]
- Kumar, S.; Singh, K.; Gupta, R.K. Coupled Higgs Field Equation and Hamiltonian Amplitude Equation: Lie Classical Approach and -Expansion Method. Pramana J. Phys. 2012, 79, 41–60. [Google Scholar] [CrossRef]
- Eslami, M.; Mirzazadeh, M. The Simplest Equation Method for Solving Some Important Nonlinear Partial Differential Equations. Acta Univ. Apulensis 2013, 33, 117–130. [Google Scholar]
- Mirzazadeh, M. Topological and Non-topological Soliton Solutions of Hamiltonian Amplitude Equation by He’s Semi-inverse Method and Ansatz Approach. J. Egypt. Math. Soc. 2015, 23, 292–296. [Google Scholar] [CrossRef]
- Mirzazadeh, M. Modified Simple Equation Method and Its Applications to Nonlinear Partial Differential Equations. Inf. Sci. Lett. 2014, 3, 1–9. [Google Scholar] [CrossRef]
- He, J.; Xu, S.; Porsezian, K. Rogue Waves of the Fokas-Lenells Equation. J. Phys. Soc. Jpn. 2012, 81, 1–4. [Google Scholar] [CrossRef]
- Fokas, A.S. On a Class of Physically Important Integrable Equations. Physica D 1995, 87, 145–150. [Google Scholar] [CrossRef]
- Lenells, J. Exactly Solvable Model for Nonlinear Pulse Propagation in Optical Fibers. Stud. Appl. Math. 2009, 123, 215–232. [Google Scholar] [CrossRef]
- Lenells, J.; Fokas, A.S. On a Novel Integrable Generalization of the Nonlinear Schrödinger Equation. Nonlinearity 2009, 22, 11–27. [Google Scholar] [CrossRef]
- Lenells, J. Dressing for a Novel Integrable Generalization of the Nonlinear Schrödinger Equation. J. Nonlinear Sci. 2010, 20, 709–722. [Google Scholar] [CrossRef]
- Kundu, A. Two-fold Integrable Hierarchy of Nonholonomic Deformation of the Derivative Nonlinear Schrödinger and the Lenells-Fokas Equation. J. Math. Phys. 2010, 51, 1–17. [Google Scholar] [CrossRef]
- Matsuno, Y. A Direct Method of Solution for the Fokas-Lenells Derivative Nonlinear Schrödinger Equation: I. Bright Soliton Solutions. J. Phys. A. 2012, 45, 1–19. [Google Scholar] [CrossRef]
- Matsuno, Y. A Direct Method of Solution for the Fokas-Lenells Derivative Nonlinear Schrödinger Equation: II. Dark Soliton Solutions. J. Phys. A. 2012, 45, 1–31. [Google Scholar] [CrossRef]
- Vekslerchik, V.E. Lattice Representation and Dark Solitons of the Fokas-Lenells Equation. Nonlinearity 2011, 24, 1165–1175. [Google Scholar] [CrossRef]
- Xu, S.; He, J.; Cheng, Y.; Porsezian, K. The n-Order Rogue Waves of Fokas-Lenells Equation. Math. Methods Appl. Sci 2015, 38, 1106–1126. [Google Scholar] [CrossRef]
- Xu, J.; Fan, E. Leading-Order Temporal Asymptotics of the Fokas-Lenells Equation without Solitons. 2013. arXiv: 1308.0755. Available online: http://arxiv.org/pdf/1308.0755.pdf (accessed on 26 August 2015).
- Zhao, P.; Fan, E. Reality Problems for the Algebro-Geometric Solutions of Fokas-Lenell Hierarchy. 2013. arXiv: 1309.2368. Available online: http://arxiv.org/pdf/1309.2368.pdf (accessed on 26 August 2015).
- Zhao, P.; Fan, E.; Hou, Y. Algebro-Geometric Solutions and Their Reductions for the Fokas-Lenells Hierarchy. J. Nonlinear Math. Phys. 2013, 20, 355–393. [Google Scholar] [CrossRef]
- Kudryashov, N.A. One Method for Finding Exact Solutions of Nonlinear Differential Equations. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Ryabov, P.N.; Sinelshchikov, D.I.; Kochanov, M.B. Application of the Kudryashov Method for Finding Exact Solutions of the High Order Nonlinear Evolution Equations. Appl. Math. Comput. 2011, 218, 3965–3972. [Google Scholar] [CrossRef]
- Lee, J.; Sakthivel, R. Exact Travelling Wave Solutions for Some Important Nonlinear Physical Models. Pramana J. Phys. 2013, 80, 757–769. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demiray, S.T.; Bulut, H. New Exact Solutions of the New Hamiltonian Amplitude-Equation and Fokas Lenells Equation. Entropy 2015, 17, 6025-6043. https://doi.org/10.3390/e17096025
Demiray ST, Bulut H. New Exact Solutions of the New Hamiltonian Amplitude-Equation and Fokas Lenells Equation. Entropy. 2015; 17(9):6025-6043. https://doi.org/10.3390/e17096025
Chicago/Turabian StyleDemiray, Seyma Tuluce, and Hasan Bulut. 2015. "New Exact Solutions of the New Hamiltonian Amplitude-Equation and Fokas Lenells Equation" Entropy 17, no. 9: 6025-6043. https://doi.org/10.3390/e17096025
APA StyleDemiray, S. T., & Bulut, H. (2015). New Exact Solutions of the New Hamiltonian Amplitude-Equation and Fokas Lenells Equation. Entropy, 17(9), 6025-6043. https://doi.org/10.3390/e17096025




