1. Introduction
Edge-independent random graphs are random graph models with independent but (possibly) heterogeneous edge probabilities, generalizing the model with constant edge probability introduced by Erdős and Rényi [
1,
2]. Given a real symmetric matrix
with
, the edge-independent random graph model
[
3] is defined as a random graph on the vertex set
, which includes each edge
with probability
independently. Clearly, the classical Erdős-Rényi random graphs and the Chung–Lu models [
4] with given expected degrees are two special examples of
.
Edge-independent random graphs are applicable in a range of areas such as modeling of social networks, and detection of community structures [
5,
6],
etc. The number of interacting nodes is typically large in practical applications, and it is appropriate to investigate the statistical properties of parameters of interest. The Estrada index and the normalized Laplacian Estrada index of
for large
n are examined in [
7]. The problem of bounding the difference between eigenvalues of
A and those of the adjacency matrix of
, together with its Laplacian spectra version, has been studied intensively recently; see, e.g., [
3,
8,
9]. It is revealed in [
9] that large deviation from the expected spectrum is caused by vertices with extremal degrees, where abnormally high-degree and low-degree vertices are obstructions to concentration of the adjacency and the Laplacian matrices, respectively. A regularization technique is employed to address this issue.
Relative entropy [
10] is a key notion in quantum information theory, ergodic theory, and statistical mechanics. It measures the difference between two probability distributions; see e.g., [
11,
12,
13,
14,
15,
16,
17] for various applications of relative entropy on physical, chemical and engineering sciences.
Inspired by the above consideration, we in this paper study the extremal degrees of the edge-independent random graph
in the thermodynamic limit, namely, as
n tends to infinity. Our approach is based on concentration inequalities, where the notation of relative entropy plays a critical role. We first build the theory for maximum and minimum degrees for
in
Section 2, and then present an application for the random graph model
with given expected degree sequence
w and a discussion regarding possible future direction in
Section 3. Various combinatorial and geometric properties of
including the hyperbolicity and warmth have been reported; see, e.g., [
18,
19,
20].
2. Bounds for Maximum and Minimum Degrees
Recall that is a real symmetric matrix. Its eigenvalues can be ordered as . Given a graph , let and be its maximum and minimum degrees, respectively. The maximum expected degree of G is denoted by , which is equivalent to the maximum row sum of A. Let and represent the maximum and minimum elements, respectively, in A. We say that a graph property holds in asymptotically almost surely (a.a.s.) if the probability that a random graph has converges to 1 as n goes to infinity.
Theorem 1. For an edge-independent random graph G, suppose that . Then Proof. The lower bound is straightforward since
by employing Theorem 1 in [
3].
For the upper bound, we set
as the degree of vertex
i in
G. By construction,
follows the sum of
n independent Bernoulli distributions. If
, the upper bound in Equation (
1) holds true trivially. Therefore, we assume
in the sequel.
For any non-decreasing function
on the interval
, the Markov inequality [
2] implies that for
,
By choosing
, we obtain from (
3) that
where
is the so-called relative entropy [
10].
Recall the Taylor expansion of
. For any
, we have
and
Now, we choose
satisfying
. Therefore, if
as
, the above comments and the inequality (
4) yield
By assumption, we have
. We choose
. Hence, the estimate (
6) implies that
asymptotically almost surely, which concludes the proof of the upper bound. ☐
Remark 1. The lower bound in (
1) is best possible according to [
3]. The upper bound in (
1) is also essentially best possible. Indeed, suppose that there exists
satisfying
a.a.s.. Given an
, we define
for all
j. Hence,
. Using the Chernoff bound, we deduce that
, which contradicts the assumption.
Remark 2. The use of Markov’s inequality in (
3) is of course reminiscent of the Chernoff bound, which is a common tool in bounding tail probabilities [
2]. However, we mention that the relative entropy
here plays an essential role that cannot be simply replaced by the Chernoff-type bounds. The Chernoff’s inequality (see, e.g., Lem. 1 in [
4]) gives
which may produce a fit upper bound only if
. The similar comments can be applied to Theorem 2 below for the minimum degree of
.
Remark 3. Notice that . It is easy to see that the upper bound holds a.a.s. provided . In fact, it suffices to take in the above proof.
Remark 4. If
for all
i and
j, the edge-independent model
reduces to the Erdős-Rényi random graph
(with possible self-loops; however, this is not essential throughout this paper). Since
, Theorem 1 implies that for
, if
, we have
a.a.s.. However, this result is already known to be true under an even weaker condition, namely,
(see, e.g., p.72, Cor. 3.14 in [
1], [
21]). It is viable to expect that our Theorem 1 holds as long as
. Unfortunately, we do not have a proof presently.
This also lends support to the conjecture made in [
3] that Theorem 1 therein (regarding the behavior of adjacency eigenvalues of edge-independent random graphs) holds when
. A partial solution in this direction can be found in [
8].
Theorem 2. Let G be an edge-independent random graph.- (A)
If , then
- (B)
If , then
Proof. The statement (B) holds directly from Theorem 1 by noting that , where is the complement of G. Since and , the upper bound in the statement (A) follows immediately from Remark 3. It remains to prove the lower bound of the statement (A).
To show the lower bound, we address three cases separately.
Case 1. . It it clear that a.a.s. in this case.
Case 2. .
For any non-decreasing function
on the interval
, the Markov inequality indicates that for
,
By choosing
, we obtain from (
8) that
where
is the relative entropy defined in the proof of Theorem 1.
In the following, we choose
and
as
. Hence, from (
9) we obtain
where in the second inequality we have used the following estimation
By assumption we set
for some
. By choosing
, we obtain
Combining (10) and (12) we arrive at as .
Finally, by our choice of parameters, as . Hence, , which completes the proof in this case.
Case 3. .
Notice that
can be viewed as a random graph in
. Hence, the same arguments towards (
4) imply that
for any
satisfying
.
In the following, we take
. Thus, the relative entropy in (
13) can be bounded below as
where
is a constant. Combining (13) and (14) we obtain
where
is a constant. Here, in the second inequality of (
15), we have employed the assumptions
and
.
Take
in the inequality (
15). It is direct to check that
and
as
under our assumptions. Hence, we have
, and
The last equality holds since . The proof is then complete. ☐
Remark 5. Similarly as in Remark 1, the upper and lower bounds of Theorem 2 are essentially best possible.
Remark 6. When
for all
i and
j, Theorem 2 reduces to the fact for Erdős-Rényi model that
a.a.s. provided
. This result is already known (see, e.g., p.152 in [
2]) and is proved by a more sophisticated method called Stein’s method. A more or less similar approach appears in [
21].
3. An Application to Random Graphs with Given Expected Degrees
The random graph model
with given expected degree sequence
is defined by including each edge between vertex
i and
j independently with probability
, where the volume
[
4,
18]. By definition we have
,
and
, where
. Moreover, let the second-order volume and the expected second-order average degree be
and
, respectively.
An application of Theorem 1 to yields the following corollary on the maximum degree of .
Corollary 1. For a random graph , suppose that . Then Proof. The results follow immediately from Theorem 1 by noting that
(see, e.g., p.163, Lem. 8.7 in [
18]). ☐
Analogously, the following result is for the minimum degree of .
Corollary 2. Let G be a random graph in .- (A)
If , then - (B)
To illustrate the availability of the above results, we study two numerical examples.
Example 1. Consider the random graph model
with
and
. This model is more or less similar to homogeneous Erdős-Rényi random graphs. It is straightforward to check that all conditions in Corollary 1 and Corollary 2 hold. In
Table 1, we compare the theoretical bounds of maximum degrees obtained in Corollary 1 with numerical values using Matlab software. The analogous results for minimum degrees are reported in
Table 2. We observe that the simulations are in line with the theory. It turns out that the upper bound for the maximum degree and the lower bound for the minimum degree are more accurate.
Table 1.
Maximum degree of with (with half of the numbers being ). The theoretical upper and lower bounds are calculated from Corollary 1. Numerical results are based on average over 20 independent runs.
Table 1.
Maximum degree of with (with half of the numbers being ). The theoretical upper and lower bounds are calculated from Corollary 1. Numerical results are based on average over 20 independent runs.
| n | Theoretical Lower Bound | | Theoretical Upper Bound |
|---|
| | | |
| | | |
| | | |
| | | |
| | | |
Table 2.
Minimum degree of with (with half of the numbers being ). The theoretical upper and lower bounds are calculated from Corollary 2. Numerical results are based on average over 20 independent runs.
Table 2.
Minimum degree of with (with half of the numbers being ). The theoretical upper and lower bounds are calculated from Corollary 2. Numerical results are based on average over 20 independent runs.
| n | Theoretical Lower Bound | | Theoretical Upper Bound |
|---|
| | | |
| | | |
| | | |
| | | |
| | | |
Example 2. Power-law graphs, which are prevalent in real-life networks, can also be constructed based on the Chung–Lu model
[
18]. Given a scaling exponent
β, an average degree
, and
, a power-law random graph
is defined by taking
for
, where
We choose , , and . It is direct to check that the conditions in Corollary 1 and Corollary 2 hold.
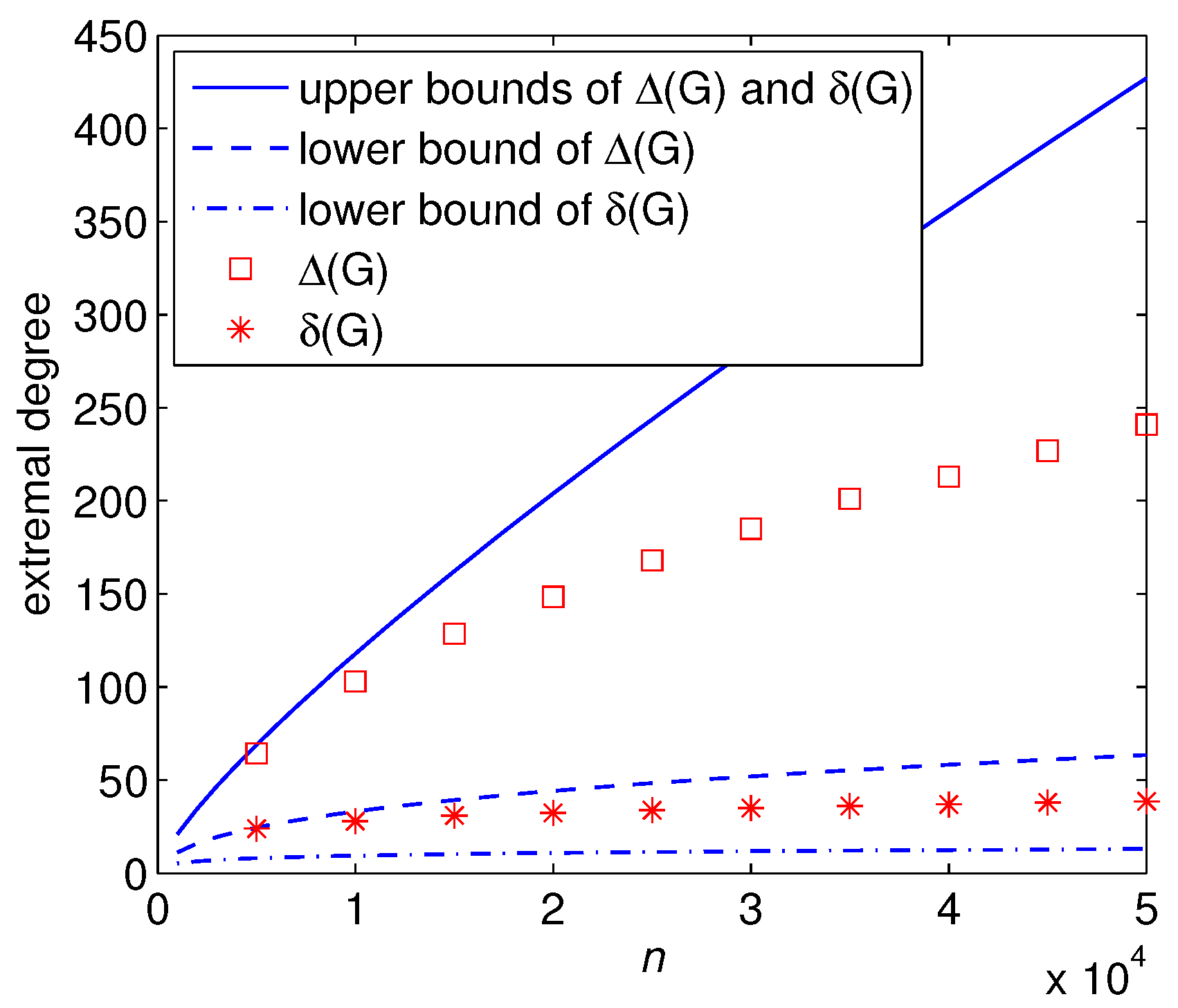
In
Figure 1 we show the maximum and minimum degrees as well as the theoretical bounds for
with different number of vertices. Note that the upper bound in (19) is worse than that in (18) for this example. We thus invoke the same upper bounds for both
and
in
Figure 1.
Figure 1.
Extremal degree versus the number of vertices n. The theoretical upper and lower bounds are from (17) and (18). Each data point is obtained by means of a mixed ensemble averaging of 30 independent runs of 10 graphs yielding a statistically ample sampling.
Figure 1.
Extremal degree versus the number of vertices n. The theoretical upper and lower bounds are from (17) and (18). Each data point is obtained by means of a mixed ensemble averaging of 30 independent runs of 10 graphs yielding a statistically ample sampling.
We observe interestingly, as in Example 1, that the upper bound for the maximum degree and the lower bound for the minimum degree seem to be more accurate. As is known that large deviation phenomena are normally associated with a global hard constraint which fights against a local soft constraint. We contend that the deviations from the expected degree sequence are due here to a fight of the constrained degree sequence with the imposed edge-independency.
Figure 2.
A depiction of the small-world graph with , , and .
Figure 2.
A depiction of the small-world graph with , , and .
As a follow up work, inspired by the above examples, it would be of interest to identify all the graphs that are close to the theoretical upper or lower bounds. As an illustrating example, we consider the small-world graph
(
) studied in [
22,
23], which can be viewed as the join of a random graph
and a ring on
n vertices, each of which has edges to precisely
k subsequent and
k previous neighbors (see, e.g.,
Figure 2). In the special case of
,
G becomes a regular graph, and we know that
, where
A is the adjacency matrix of
G. If
holds, it follows from Theorem 1 that
Clearly, the upper bound is close if
k is large, while the lower bound tends to be more accurate if
k is small. In general, when
holds, for any
it follows from Theorem 1 that
Note that the second largest eigenvalue of the adjacency matrix of
, which is a circulant matrix, is
as
. Utilizing the edge version of Cauchy’s interlacing theorem, (22) and (23), we derive the following estimation
The gap between upper and lower bounds can be quite close provided k attains it maximum, namely, .