1. Introduction
Many systems in nature and society reveal network organizations. These networks, such as biological protein networks [
1], science collaborations [
2,
3], social networks [
4] and the Internet [
5], have been found to represent some attributes, such as scale free, small world,
etc. These discoveries emerge from the science of complex networks. Recent studies have revealed that object-oriented software systems share some structural attributes with these complex networks. Specifically, the networks of software systems are characterized by a scale-free degree distribution [
6,
7,
8,
9,
10], a small-world structure (short average path length and high clustering) [
11,
12] and some other features [
13,
14,
15,
16,
17,
18]. This therefore raises the study of software networks in recent years.
Software systems consist of many interacting units at some levels of granularity, such as methods, classes and subsystems [
19]. Additionally, the collaborations of these units in a software system can be therefore extracted and defined as a software network.
Figure 1 shows a simple example of the extraction from a software system to a software network, in which the classes in the left figure are nodes and the collaborations of such nodes are edges. For the software systems with a more complex structure, the corresponding software networks are organized to be highly functional, modularized [
19] and evolvable [
15]. This therefore brings some further studies on software networks, such as community detection [
20,
21], quality assessment [
10], important unit identification [
22], bug classification [
23] and developer social collaboration [
24,
25], which are helpful to various phases in software engineering practices.
During the whole production process of a software project, the design phase is the most critical stage because the structure of the units at different levels and the collaborations of such units are explicitly described in this process. These collaborations enable the detailed functional tasks to be integrated by many reusable basic units in a modular and hierarchical fashion [
11]. However, some other crucial and persistent actions in the lifecycle of software systems, such as software maintenance, refactoring and adaptation, cannot be carried out in the task of software design, but lie in the formation of software systems. The goal of a software project is not only building up a software system to satisfy the functional requirement, but also making the software systems convenient and economical to upgrade to new versions. Thus, it makes the evolution of software networks an increasingly important issue.
However, while active research has been undertaken and many solid results have been obtained for understanding the formation mechanisms of these natural and man-made systems, the same work has been only very sparsely performed on software systems, and little has been achieved about the cause-effect relationship between software engineering practices and the structure of these systems.
From the view of software engineering, software evolution is a process of meeting the dynamical requirement changes of the users. From the view of entropy, software evolution is a process of network structural change from chaos to order. As a kind of typical open system, the structure of software systems is dynamically changing under an external driving force, and the changing reveals the status of system designing and coding [
26]. Therefore, studying how the software systems evolve can help in a number of areas, including software testing, software maintenance and program comprehension [
27] and further to evaluate the system robustness and its ability to tolerate changes [
28].
Based on various of empirical studies [
15,
29,
30,
31,
32,
33,
34,
35], a few models of software network evolution, which describe the evolutionary mechanism from different perspectives, have been proposed. The models reported in [
11,
36,
37,
38,
39] are respectively based on refactoring processes, node aging affect, weighted network and software patterns. These models perform well in some aspects of software network evolution, and the work can forecast the evolution trends based on the model [
39]. However, they do not explicitly include some important qualities of software networks, e.g., modularity and hierarchy. In reality, however, software systems are characterized by high modularity [
11,
21,
40], which corresponds to the important principle of high cohesion and low coupling in software design [
41], and the practice of software architecture design assures that software networks are hierarchical and multigranular by nature [
13,
42,
43,
44]. In addition, most of these models adopt a undirected graph, which is appropriate for some types of networks, such as the Internet and social networks, to represent software networks. However, software networks are directed because dependent relations between basic units in software systems are unidirectional, and the direction is designated when the node is added to the network [
45].
Here, we stress another salient fact about the evolution of software systems, which is missing in most of the existing models. With respect to evolution, these systems lie somewhere between natural systems, which are characterized by a bottom-up self-organizing process, and conventional engineering systems, whose upgrades are governed by a top-down central design, because the work of software design is a social work in which many designers and developers are working together to carry out the task [
24]. On the one hand, software architecture supports more autonomous attachments in comparison to other types of architecture, because objects are loosely coupled, and adding or removing non-core objects usually does not significantly affect the rest of the system. On the other hand, in enhancing software systems, some issues should be taken into consideration, such as reuse, maintenance, performance and optimization. They all call for a comprehensive viewpoint and overall design.
In view of the current situation discussed above, we aim at more accurately understanding the general mechanism that governs the evolution of software systems and exploring the cause-effect relationship between a variety of software development principles and the structure of software systems. To accomplish this goal, we have developed a multi-level model of software evolution, which represents software systems as directed networks and adopts a modular binding process for new component attachments.
The rest of this paper is structured as follows. In
Section 2, we describe the multi-level model, in terms of structure and the evolutionary mechanism.
Section 3 exhibits simulation results based on the model and compares them to empirical data. In
Section 4, we explore the implications of various software design principles for the structure of software systems.
Section 5 concludes this work and presents possible future works.
2. The Multi-Level Model of Software Evolution
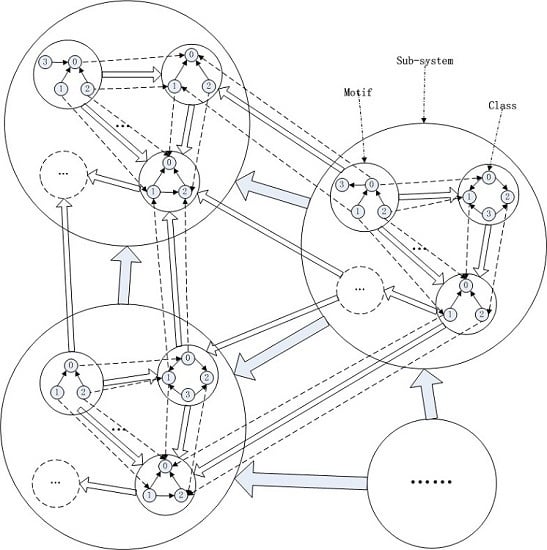
2.1. Levels of Software Systems
Software systems are multi-level systems by nature. In this work, we consider three typical levels of software systems, which are outlined in
Table 1.
We represent a software system on each level as a directed graph . Here, V is a set of elements that are termed nodes; E is a set of ordered node pairs, each of which implies that the first node depends on the second one, and this relation of dependence is depicted as an edge that leaves the first and enters the second node. The sets of elements on Levels I, II and III are denoted respectively by , , and . Therefore, the element on Level I is the i-th element of on Level II, and in turn is the j-th element of on Level III, which is the k-th element on this largest scale.
In the following part of this section, we will give more detailed descriptions of the three levels.
2.1.1. Level I
In software systems, some basic units, such as classes, encapsulate fundamental functions for constructing more complex and application-specific elements on larger scales. We term the scale corresponding to these units Level I.
Collaborations among these basic elements form the microstructure of a software system. Specifically, there are two types of dependencies between these elements: inheritance implies a relationship of “is a”, and association corresponds to “has a”. We follow the convention of software engineering in depicting a dependence: an edge is directed from Element B to Element A if B, in its definition, makes reference to (or is dependent on) A. In our analysis, repeated links are not considered.
2.1.2. Level II
In software practices, some combinations of classes or other basic units appear with much higher frequencies than would be expected by pure chance [
42], although some do not work in modern software engineering [
46]. These patterns, such as motifs, are usually composed of a few basic (Level I) elements. They are general repeatable solutions to some commonly-occurring problems in software design or have been reused over time in different systems to perform various information processing functions. Being building blocks of more complex software structures, they constitute a natural level between the basic units, such as classes, and the entire software system. We name it Level II.
In reality, Level II elements are usually composed of three or four Level I elements. An important fact is that Level II elements with few internal links appear more frequently than those with many internal connections [
42]. The high probability of these sparse graphs is caused by the software engineering principle that coupling should be minimized [
47]. The most commonly-used Level II elements are displayed in
Figure 2.
2.1.3. Level III
Component-based software engineering has become a widely-adopted reuse-oriented approach to software development, and software evolution usually involves adding new components to existing systems. In comparison with single classes that can be used only if the detailed knowledge about them is known, components are more encapsulated, abstract and easy to use.
In our model, components lie on Level III. They contain different numbers of Level II elements and eventually different numbers of Level III elements, conforming to the empirical fact that the sizes of components vary from a few objects to whole applications.
2.2. The Mechanism of Software Evolution
Empirically, software networks keep growing in response to changing conditions and new requirements, in line with the empirical studies on a large number of real software systems [
48,
49]. Consequently, new functional modules are continually added into software systems, and these elements are much more than those that are removed. The work in [
44] further reported that, in real software systems, both elements and edges tend to grow on different levels simultaneously.
There is an empirical fact that, although newly-added elements have different functions and sizes, the numbers of the edges between them and the existing elements are quite close to one another. For simplicity, we consider these numbers as equal and treat them as a constant that is denoted by . Its value can be obtained by averaging the corresponding values of the elements in different systems.
There are a few parameters in our model: reuse probability Γ, common to elements on all three levels, expresses the general degree of reuse; coupling ratio Λ is the ratio of the number of the edges that connect all of the Level II elements within the same Level III element to all of the Level II edges related to the Level III element; the total size of the whole software system at the end of the evolution , in terms of the number of Level I elements; and the minimum size and maximum size of the Level III elements, in terms of the number of Level I elements.
The mechanism of evolution can be described as the following algorithm and correspondingly depicted as
Figure 3. One should note that an edge between two Level II elements is established because two Level I elements separately belonging to the two Level II elements are connected. Likewise, an edge between two Level III elements is established because two Level II elements separately belonging to the two Level II elements are connected.
- Step 1
Determine the values of , , , Λ and Γ.
- Step 2
Create a new Level III element with a random size .
- Step 2.1
In , create a new Level II element of a random type.
- Step 2.2
Link to an existing Level II element in with directions depending on Γ. The existing element is selected by probability or .
- Step 2.3
With the determined direction, link
(see
Section 2.2.5) pairs of Level I elements between
and the existing element.
- Step 2.4
If has linked to existing Level II elements in , continue; else, go to Step 2.2.
- Step 2.5
If the number of Level III elements in reaches , go to Step 3; else, go to Step 2.1.
- Step 3
Attach to an existing Level III element with directions depending on Γ. It is selected with probability or .
- Step 3.1
Select a Level II element from , and link to an existing Level II element in the existing Level III element by probability or .
- Step 3.2
With the determined direction, link pairs of Level I elements between and the existing Level II element.
- Step 3.3
If
(see
Section 2.2.4) pairs of Level II elements have been linked between
and the existing Level III element, go to Step 4; else, go to Step 3.1.
- Step 4
If the number of Level III elements in all Level I elements reaches , go to Step 5; else, go to Step 2.
- Step 5
End the process.
In the rest of this section, we present a more detailed explanation of the mechanism.
2.2.1. Direction of Attachment
The direction of the edges is determined in the following manner: (1) it will reuse an existing module and establish an outgoing edge with reuse probability Γ; (2) it depends on an existing module and receives an incoming edge with probability . Γ is positively related to the general degree of reuse. We adopt a great value for Γ on account of the fact that, in the software development practice, there is a strong inclination to reuse.
2.2.2. Probability of Attachment
In software engineering practices, the elements with high incoming dependencies usually have a simple structure and perform some fundamental functions. These elements could be reused for a greater probability to be reused and receive incoming links. In contrast, the elements with more outgoing dependencies, such as modules of user interfaces, usually represent a more complex structure within the elements. They are more likely to depend on other elements and establish outgoing links. Due to their complexity, it is dangerous for the system if these elements are dependent on other elements.
Consequently, elements with larger in-degrees are more likely to receive incoming edges, while those with larger out-degrees are more likely to link to other elements with outgoing edges [
45]. Therefore, we can consider that the probability that an element receives an incoming edge
is proportional to its in-degree
, and that with which elements establish an outgoing edge
is proportional to its out-degree
,
i.e.,
and:
2.2.3. Level III
We assume that Level I elements will be added to the existing network. New Level III elements with a random number of Level I elements will be generated and added, one by one, to the existing network, until the total number of Level I elements of the whole system reaches . The size of each Level III element is between and , and there are edges that connect this element to other existing Level III elements.
2.2.4. Level II
The edges of each Level II element are of two types: internal edges connecting it to other elements in the same Level III element and edges that link to elements in other Level III elements. We use the parameter named coupling ratio Λ for the proportion of the second type of edges. A high (low) value of Λ therefore corresponds to high coupling and low cohesion (low coupling and high cohesion).
In the evolutionary process, when a new Level II element is added into a Level III element , internal edges form between and other Level II elements in . Since contains Level II elements, there will be internal edges and edges connecting different Level II elements within .
When an edge is added between the new Level III element and an existing Level III element, pairs of Level II elements between the two Level III elements are linked through Level II edges and with the same direction as the Level III edge. The probabilities for each pair of Level II elements to get an incoming edge and an outgoing edge are and , respectively.
2.2.5. Level I
Empirically, a Level II element is composed of three or four Level I elements of 14 types (see
Figure 2). When a Level II element is generated, the number of internal Level I edges depends on the type of the Level II element. For simplicity, we assume that the 14 types of Level I elements appear in every Level II element with an equal probability. Consequently, we can get the average number of Level I elements
and the average number of Level I edges
.
We assume that there are
Level II elements in the current Level III element, and
Level I level interacting edges are added when a Level II level edge is added. The total number of Level I edges is equal to the sum of the total number of internal edges and the total number of interacting edges:
then we have:
We can therefore simply consider that each Level II element contains Level II elements and Level II edges. When an edge is added between the new Level II element and an existing Level II element, pairs of edges between the two elements are linked by Level I level edges and with the same direction as that of the Level II level edge. The selected probabilities for each pair of elements to get the incoming edge and the outgoing edge are and , respectively.
3. Simulation Results
In this section, some essential results of simulations based on our multi-level model are displayed. The simulations were undertaken with respect to the structural properties of our simulated software network. We explored the influences of four parameters: coupling ratio Λ, reuse probability Γ and the minimum size and the maximum size of the Level III elements. The values for and are adopted as, respectively, the average values of their corresponding empirical observations.
For validating our modeling, the simulation results are compared to data presented in some real-world software systems, such as Blender, Doxygen, Eclipse, etc. More importantly, these simulations enable more comprehensive understanding of the evolutionary mechanisms under study.
3.1. Degree Distributions
The degree of an element, , is the number of edges attached to it. Correspondingly, the in-degree and the out-degree are respectively the number of links that enter it and the number of links that exit it.
In this study, the measurements of the
p-value and
are used to measure the goodness-of-fit for degree distributions [
50] (the code can be found from [
51]). The first metric,
p-value, represents the mathematical “distance” between the power-law distribution and the distribution of the actual network. The previous study reports that the power-law distribution of the current data can be believable, if
p-value
; conversely, it cannot be authentic [
50]. moreover, the degree distribution has some non-power-law behavior at the lower end; thus, we use the metric of
to control the part of the degree distribution that represents power-law behavior. It is reported that the power-law distribution is more plausible if the value of
is smaller [
50].
Figure 4 shows the simulated distribution of the degrees of the Level I elements, and the corresponding correlation coefficients,
p-value,
can be found in
Table 2. For comparison, in the same figure, we also plotted the degree distribution of the real software systems. It can be seen that both of and simulations and real software networks represent a power-law feature, and the degree distributions of the simulations are close to those of real software networks because the values of the exponents
γ are close to the values of real software networks.
The power-law degree distribution is an important network feature in complex networks. It indicates that the degrees of most of the nodes are small while a small amount of nodes have large degrees [
52]. In software networks, the elements with a small degree can be benefit fromthe function decomposition [
53]. In contrast, the nodes with a large degree are crucial to achieve complex tasks and frequently interact and exchange data with other nodes. Therefore, the possible failures of these nodes with a large degree could greatly affect the system.
On the other hand, we know that software networks are directed; thus, the in-degree and out-degree distributions can also represent the interaction characteristics of the nodes.
Figure 5 and
Table 3 show the simulated distribution of the in-degrees of the Level I elements, with the comparison of the in-degree distribution of the real software systems. Similar to the degree distributions, the in-degree distributions of the simulations and real software networks express the power-law, and the differences between them are small according to the exponents
γ and fitting goodness
p-value. Additionally,
Figure 6 and
Table 4 show the out-degree distributions of these networks. Though the distributions are also close between the simulations and real software networks, the fitting goodness of the power-law is not good enough for some networks. Therefore, only some software networks follow a power-law.
3.2. Correlation between In-Degree and Out-Degree
In comparison with some other complex networks, software networks display an important characteristic: in-degrees and out-degrees of elements are negatively correlated [
11].
Figure 7 is a scatter plot of the simulated Level I in-degrees against corresponding out-degrees of all Level I elements. For comparison, in the same figure, we also plotted the same types of data obtained from the real software systems. This figure expresses that the results generated by our model are in line with empirical data.
We can see that the elements with larger in-degrees have smaller out-degrees, while the nodes with large out-degrees have smaller in-degrees. Therefore, we use correlation coefficient
for measuring the correlation between in-degree and out-degree distributions. The correlation coefficients of the in-degree set and the out-degree set (respectively for all nodes and the elements with
or
) for simulations of the multi-level model and real software networks are shown in
Table 5. It can be seen that most of the coefficients for simulations (
) between in-degrees and out-degrees are close to the real software networks (
), though the negative correlations are not obvious. However, the correlation coefficients for simulations (
) between in-degrees and out-degrees are also close to the real software networks (
) and negatively correlated.
This negative correlation can be accounted for by some principles of software development. In a software system, elements with a large in-degree usually perform fundamental or commonly-used functions. These elements are therefore more likely to be reused. Conversely, elements with a large out-degree usually accomplish specific tasks. Therefore, they are less likely to be aggregated by other elements.
As shown in
Figure 7, our model also reproduced another feature of real software systems,
i.e., the largest out-degrees of the nodes are always much smaller than the largest in-degrees. In contrast, the BAmodel is unable to generate this attribute.
The reason for this feature is that elements that have a larger probability to be reused tend to have a higher in-degree; while existing elements are not easy to aggregate intonew elements. Additionally, a new element is more likely to reuse an element with many incoming links than a complex element with many outgoing links. The software engineering practice encourages reuse, which leads to large in-degrees. Conversely, it is not encouraged for an element to have too many out-degrees, because this will lead to highly complicated structures and hinder maintenance.
3.3. Level of Clustering and Modularity
In software design, the cohesion and coupling reflect the interactions between modules of software systems. Cohesion is a property of a single module and represents the degree to which the related units within the module, while coupling is a property of a pair of modules and represents the degree of relationships between such modules [
41]. It is well known that the modularized software systems are much easier to develop and maintain, and a well-modularized software system usually represents a high degree of cohesion and a low degree of coupling [
19,
20].
According to the previous studies, the metrics of the clustering coefficient and modularity are used to represent the degree of cohesion and coupling for software networks [
11,
21]. The clustering coefficient of the entire network is a measure of the degree to which nodes in the network tend to cluster together, and it represents the tendency of the nodes’ neighbors to be their common neighbors in a network [
11]. The modularity is an attribute of how good a network is divided into modules, and a good division is more edges within modules and fewer edges between them [
54]. Comparatively speaking, the clustering coefficient tends to describe the clustering of the node and its neighbors, while the modularity emphasizes the goodness of module division.
The measurement of clustering coefficient
C is the average of the clustering coefficients of all of the nodes [
55]. The equation of the clustering coefficient is:
in which
is the number of nearest neighbors of node
and
is the number of connections between them. If the value of
C is larger, the network tends to have a higher degree of cohesion and a lower degree of coupling.
Real software systems are modular, and the clusters represent some units that collaborate together to carry out the same task [
56]. Then, we choose the sample software systems, such as Blender (written in C++) and Eclipse (written in Java), respectively, to generate 10 simulated networks for comparisons, and the results are shown in
Table 6 and
Table 7.
Table 6 shows that the
C value from our model is close to the value of the real-world software system. The reason is that the networks generated by the model are modular and have high cohesion.
The work in [
21] proves that software networks show the feature of community structure by empirical studies, and thus, it is verified that software networks are modularized and that each consists of a network of interdependent parts [
57]. Therefore, we use the metric of modularity
Q, which is defined as the fraction of the edges within the divided groups minus the expected fraction of such edges in the network formed in a random way [
54], to measure the modularity of software networks. The mathematical definition for modularity
Q [
58] is:
where
denotes the weight of an edge between a node
and a node
(the weight is one in this case) in the graph,
is the sum of the weights of the edges attached to the node
,
is the community to which the node
is assigned, the function
is one if
and zero otherwise and
. The lager the value of
Q, the higher the degree of cohesion for a network.
The examples of Blender and Eclipse are also used here to study the modularity of the simulations, and the results can be found in
Table 7. We can see that the values of modularity are close between the real software networks and simulations. Moreover, the results also demonstrate that the model can produce software networks following the principle of high cohesion and low coupling.
5. Conclusions
The main contribution of this paper is that a multi-level model for software network evolution is proposed. In this model, three levels of elements, including class level, design pattern level and framework level, are used to describe the organization of the software systems. Through the comparisons with the real software networks from different aspects, the model has been proven to be inherently close to describing the formation process of real software systems. Furthermore, with the help of this model, we discuss some principles in software engineering practices, such as the relation of cohesion and coupling, the code reuse and modularity and the influence of motifs on software structure. This model could help us to understand the formation of the complex software systems and potentially to forecast the changes of the software structure.
However, some limitations may shorten the usage of the model. The parameters used in this model are obtained from the history data of the source codes. This means that the model may not correctly describe the structural changes due to the dramatic changes in the software architecture modifications. In addition, empirical studies tell us that the number of nodes and edges usually keeps increasing in most software projects, but it cannot avoid the sudden reduction of the nodes and edges in some projects for some unpredictable reasons. Besides, some large-scale software systems may not organize by three levels, but four levels or more, so how to dynamically describe the levels of the software network structure is also an open question.
Thus, some further studies still need to be done in the future. Firstly, more software projects should be investigated, especially the software systems written in the C language. Secondly, many projects have been terminated because of different reasons; thus, the studies of the structural changes of these software systems may make sense, then the model may be improved due to the further studies. Finally, the model may potentially be used to describe the formation of some other complex systems (such as the Internet, social networks, biology systems), and thus, it is worth updating the model to be universal for multi-level complex systems.