MoNbTaV Medium-Entropy Alloy
Abstract
:1. Introduction
2. Computational Methodologies and Experimental Procedures
3. Results
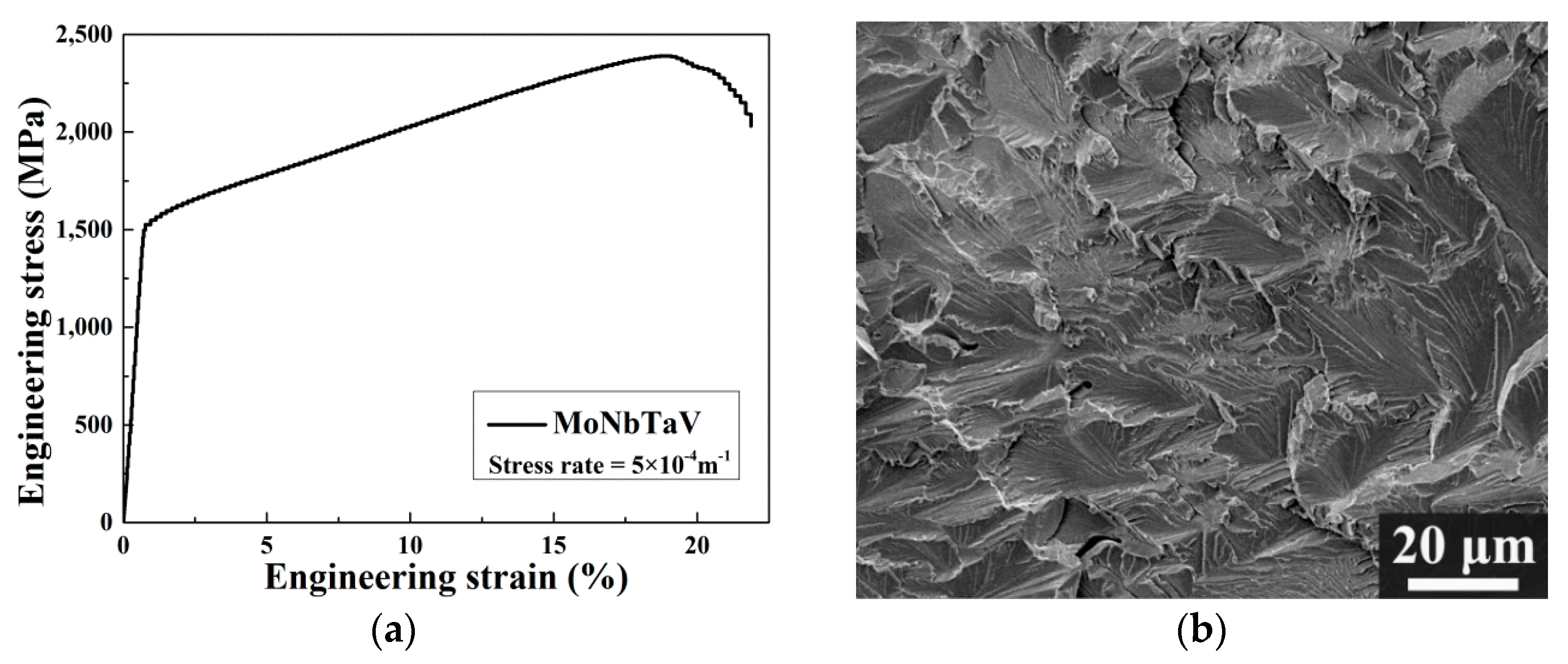
3.1. Microstructure
3.2. CALPHAD Modeling
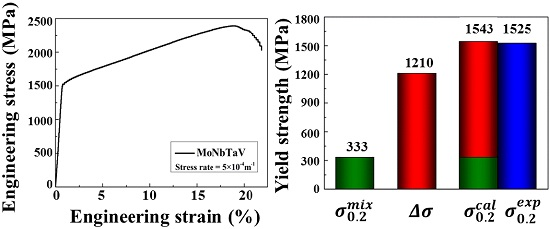
3.3. Mechanical Properties
4. Discussion
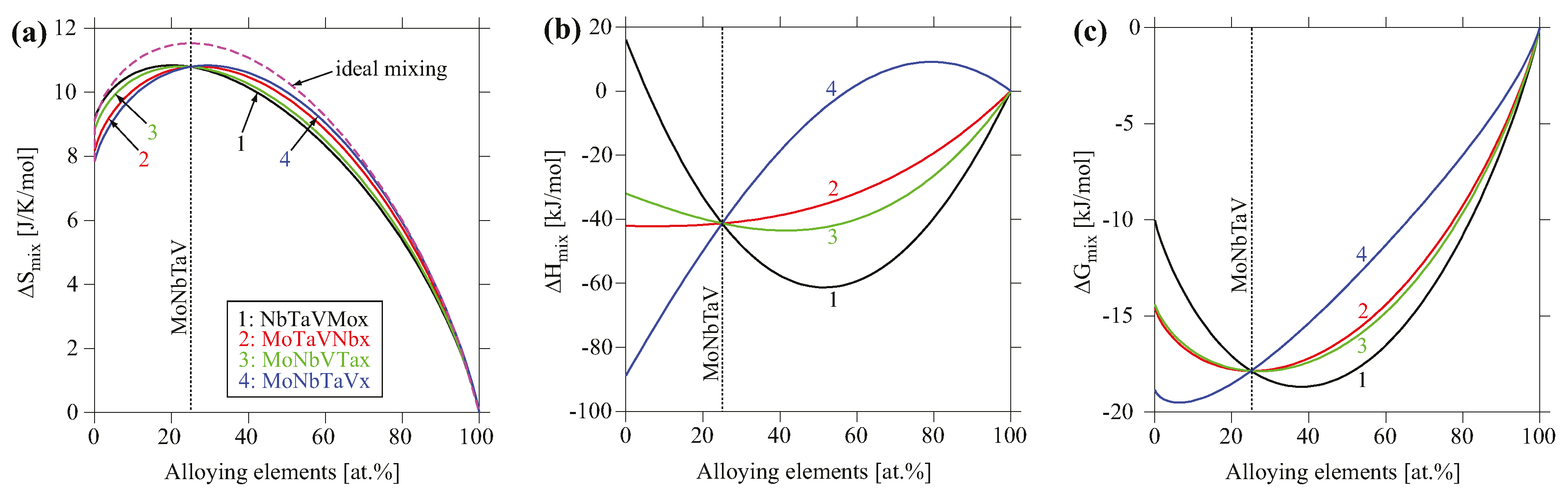
4.1. Phase Formation
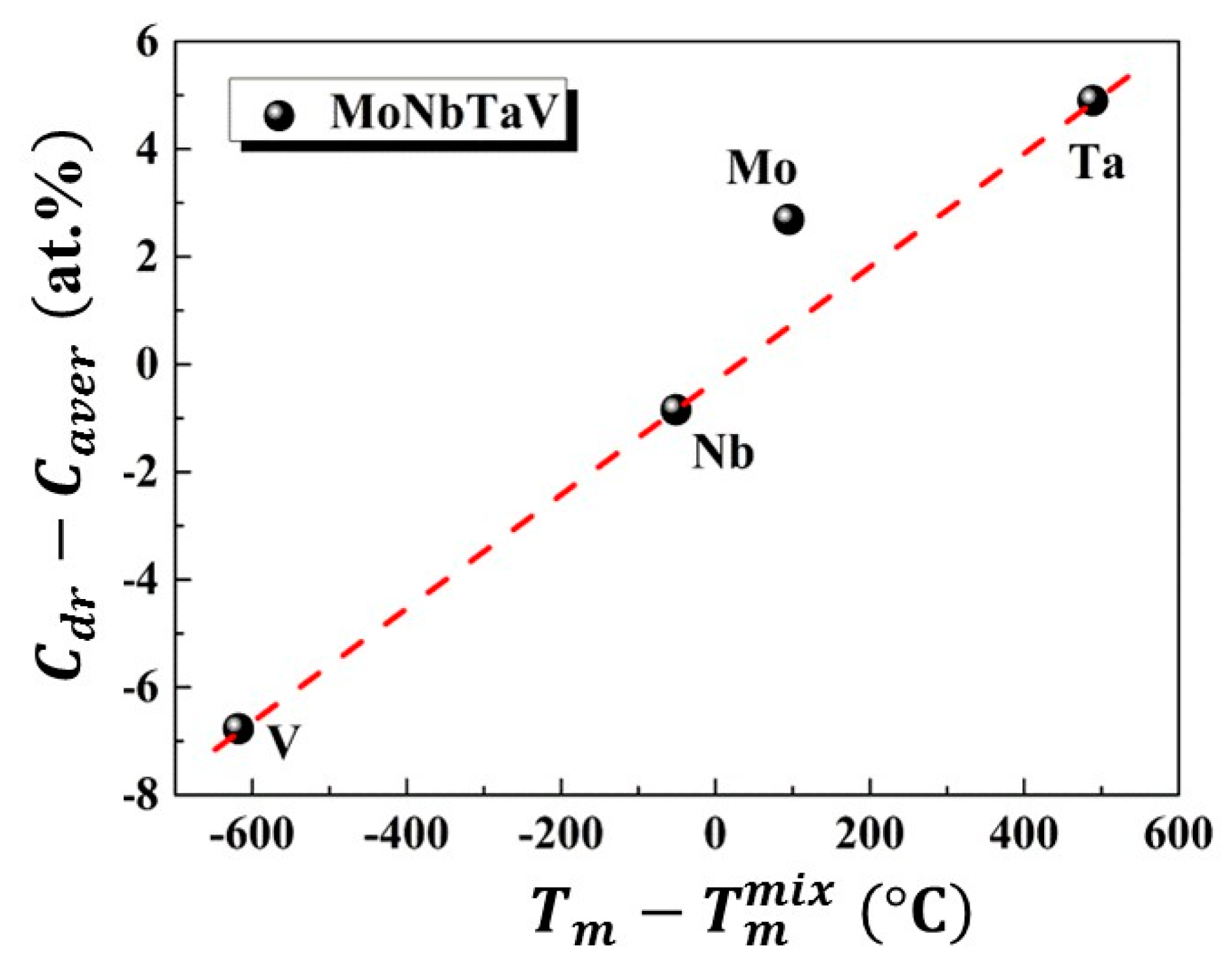
4.2. Thermodynamic Properties Analyses
4.3. Solid Solution Strengthening (SSS)
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Donachie, M.J.; Donachie, S.J. Superalloys: A Technical Guide; ASM International: Materials Park, OH, USA, 2002. [Google Scholar]
- Pollock, T.M.; Tin, S. Nickel-based superalloys for advanced turbine engines: Chemistry, microstructure and properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar]
- Yeh, J.-W.; Chen, S.-K.; Lin, S.-J.; Gan, J.-Y.; Chin, T.-S.; Shun, T.-T.; Tsau, C.-H.; Chang, S.-Y. Nanostructured High-Entropy Alloys with Multiple Principal Elements: Novel Alloy Design Concepts and Outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid—Solution phase formation rules for multi-component alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Ye, Y.F.; Wang, Q.; Lu, J.; Liu, C.T.; Yang, Y. High-entropy alloy: Challenges and prospects. Mater. Today 2015, in press. [Google Scholar] [CrossRef]
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375, 213–218. [Google Scholar] [CrossRef]
- Senkov, O.N.; Wilks, G.B.; Miracle, D.B.; Chuang, C.P.; Liaw, P.K. Refractory high-entropy alloys. Intermetallics 2010, 18, 1758–1765. [Google Scholar] [CrossRef]
- Takeuchi, A.; Amiya, K.; Wada, T.; Yubuta, K.; Zhang, W. High-entropy alloys with a hexagonal close-packed structure designed by equi-atomic alloy strategy and binary phase diagrams. JOM 2014, 66, 1984–1992. [Google Scholar] [CrossRef]
- Gao, M.C.; Zhang, B.; Guo, S.M.; Qiao, J.W.; Hawk, J.A. High-entropy alloys in hexagonal close-packed structure. Metall. Mater. Trans. A 2016. [Google Scholar] [CrossRef]
- Zhao, Y.J.; Qiao, J.W.; Ma, S.G.; Gao, M.C.; Yang, H.J.; Chen, M.W.; Zhang, Y. A hexagonal close-packed high-entropy alloy: The effect of entropy. Mater. Des. 2016, 96, 10–15. [Google Scholar] [CrossRef]
- Gao, M.C. Design of High-Entropy Alloys. In High-Entropy Alloys: Fundamentals and Applications; Gao, M.C., Yeh, J.W., Liaw, P.K., Zhang, Y., Eds.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Yeh, J.W. Recent progress in high entropy alloys. Ann. Chim. Sci. Mat. 2006, 31, 633–648. [Google Scholar] [CrossRef]
- Zhang, Y.; Zuo, T.T.; Tang, Z.; Gao, M.C.; Dahmen, K.A.; Liaw, P.K.; Lu, Z.P. Microstructures and properties of high-entropy alloys. Prog. Mater. Sci. 2014, 61, 1–93. [Google Scholar] [CrossRef]
- Murty, B.S.; Yeh, J.W.; Ranganathan, S. High Entropy Alloys; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef] [PubMed]
- Qiao, J.W.; Jia, H.L.; Liaw, P.K. Metallic glass matrix composites. Mater. Sci. Eng. R. 2016, 100, 1–69. [Google Scholar] [CrossRef]
- Senkov, O.N.; Scott, J.M.; Senkova, S.V.; Miracle, D.B.; Woodward, C.F. Microstructure and room temperature properties of a high-entropy TaNbHfZrTi alloy. J. Alloys Compd. 2011, 509, 6043–6048. [Google Scholar] [CrossRef]
- Tian, F.Y.; Varga, L.K.; Chen, N.X.; Shen, J.; Vitos, L. Ab initio design of elastically isotropic TiZrNbMoVx high-entropy alloys. J. Alloys Compd. 2014, 599, 19–25. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, Y.; Liaw, P.K. Microstructure and compressive properties of NbTiVTaAlx high entropy alloys. Procedia Eng. 2012, 36, 292–298. [Google Scholar] [CrossRef]
- Gao, M.C.; Carney, C.S.; Doğan, Ö.N.; Jablonksi, P.D.; Hawk, J.A.; Alman, D.E. Design of Refractory High-Entropy Alloys. JOM 2015, 67, 2653–2669. [Google Scholar] [CrossRef]
- Gao, M.C.; Zhang, B.; Yang, S.; Guo, S.M. Senary Refractory High-Entropy Alloy HfNbTaTiVZr. Metall. Mater. Trans. A 2016. [Google Scholar] [CrossRef]
- Senkov, O.N.; Wilks, G.B.; Scott, J.M.; Miracle, D.B. Mechanical properties of Nb25Mo25Ta25W25 and V20Nb20Mo20Ta20W20 refractory high entropy alloys. Intermetallics 2011, 19, 698–706. [Google Scholar] [CrossRef]
- Gao, M.C.; Doğan, Ö.N.; King, P.; Rollett, A.D.; Widom, M. The first-principles design of ductile refractory alloys. JOM 2008, 60, 61–65. [Google Scholar] [CrossRef]
- Gao, M.C.; Suzuki, Y.; Schweiger, H.; Doğan, Ö.N.; Hawk, J.; Widom, M. Phase Stability and Elastic Properties of Cr-V Alloys. J. Phys. Condens. Matter 2013, 25, 075402. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow. Available online: http://www.goodfellow.com (accessed on 17 May 2016).
- Sundman, B.; Jansson, B.; Andersson, J.O. The thermo-calc databank system. Calphad 1985, 9, 153–190. [Google Scholar] [CrossRef]
- Zhang, B.; Gao, M.C.; Zhang, Y.; Yang, S.; Guo, S.M. Senary Refractory High-Entropy Alloy MoNbTaTiVW. Mater. Sci. Technol. 2015, 31, 1207–1213. [Google Scholar] [CrossRef]
- Zhang, B.; Gao, M.C.; Zhang, Y.; Guo, S.M. Senary Refractory High-Entropy Alloy CrxMoNbTaVW. Calphad 2015, 51, 193–201. [Google Scholar] [CrossRef]
- Zhang, C.; Gao, M.C. CALPHAD Modeling of High-Entropy Alloys. In High-Entropy Alloys: Fundamentals and Applications; Gao, M.C., Yeh, J.W., Liaw, P.K., Zhang, Y., Eds.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Yao, H.W.; Qiao, J.W.; Gao, M.C.; Hawk, J.A.; Ma, S.G.; Zhou, H.F.; Zhang, Y. NbTaV-(Ti, W) Refractory High Entropy Alloys. Mater. Sci. Eng. A 2016. submitted. [Google Scholar]
- Zhang, C.; Zhang, F.; Chen, S.; Cao, W. Computational thermodynamics aided high-entropy alloy design. JOM 2012, 64, 839–845. [Google Scholar] [CrossRef]
- Gao, M.C.; Alman, D.E. Searching for next single-phase high-entropy alloy compositions. Entropy 2013, 15, 4504–4519. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, C.; Chen, S.L.; Zhu, J.; Cao, W.S.; Kattner, U.R. An understanding of high entropy alloys from phase diagram calculations. Calphad 2014, 45, 1–10. [Google Scholar] [CrossRef]
- Vegard, L. Die konstitution der mischkristalle und die raumfüllung der atome. Z. Phys. A Hadron. Nucl. 1921, 5, 17–26. (In German) [Google Scholar]
- Gulliver, G.H. The quantitative effect of rapid cooling upon the constitution of binary alloys. J. Inst. Met. 1913, 9, 120–157. [Google Scholar]
- Scheil, E. Comments on the layer crystal formation. Z. Metallkd. 1942, 34, 70–72. (In German) [Google Scholar]
- Yang, X.; Zhang, Y. Prediction of high-entropy stabilized solid-solution in multi-component alloys. Mater. Chem. Phys. 2012, 132, 233–238. [Google Scholar] [CrossRef]
- Martienssen, W.; Warlimont, H. Springer Handbook of Condensed Matter and Materials Data; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Takeuchi, A.; Inoue, A. Classification of bulk metallic glasses by atomic size difference, heat of mixing and period of constituent elements and its application to characterization of the main alloying element. Mater. Trans. 2005, 46, 2817–2829. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, X.; Liaw, P.K. Alloy design and properties optimization of high-entropy alloys. JOM 2012, 64, 830–838. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, Z.P.; Ma, S.G.; Liaw, P.K.; Tang, Z.; Cheng, Y.Q.; Gao, M.C. Guidelines in predicting phase formation of high-entropy alloys. MRS Commun. 2014, 4, 57–62. [Google Scholar] [CrossRef]
- Guo, S.; Ng, C.; Lu, J.; Liu, C.T. Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys. J. Appl. Phys. 2011, 109, 103505. [Google Scholar] [CrossRef]
- Guo, S.; Liu, C.T. Phase stability in high entropy alloys: Formation of solid-solution phase or amorphous phase. Prog. Nat. Sci. 2011, 21, 433–446. [Google Scholar] [CrossRef]
- Dong, Y.; Lu, Y.; Jiang, L.; Wang, T.; Li, T. Effects of electro-negativity on the stability of topologically close-packed phase in high entropy alloys. Intermetallics 2014, 52, 105–109. [Google Scholar] [CrossRef]
- Gao, M.C.; Niu, C.; Jiang, C.; Irving, D.L. Applications of Special Quasi-Random Structures to High-Entropy Alloys. In High-Entropy Alloys: Fundamentals and Applications; Gao, M.C., Yeh, J.W., Liaw, P.K., Zhang, Y., Eds.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Labusch, R. A statistical theory of solid solution hardening. Phys. Status Solidi B 1970, 41, 659–669. [Google Scholar] [CrossRef]
- Toda-Caraballo, I.; Rivera-Díaz-del-Castillo, P.E. Modelling solid solution hardening in high entropy alloys. Acta Mater. 2015, 85, 14–23. [Google Scholar] [CrossRef]
- Gypen, L.A.; Deruyttere, A. Multi-component solid solution hardening. J. Mater. Sci. 1977, 12, 1028–1033. [Google Scholar] [CrossRef]







| Metal | Mo | Nb | Ta | V | MoNbTaV (Calc/Exp) |
|---|---|---|---|---|---|
| (Å) | 3.1468 | 3.301 | 3.303 | 3.039 | 3.2036/3.208 |
| (Å) | 1.4 | 1.47 | 1.47 | 1.35 | – |
| (°C) | 2623 | 2477 | 3017 | 1910 | 2528/– |
| (MPa) | 1530 | 1320 | 873 | 628 | 1097/4947 |
| (MPa) | 438 | 240 | 345 | 310 | 333/1525 |
| 6 | 5 | 5 | 5 | – | |
| ∆χ | 2.16 | 1.6 | 1.5 | 1.63 | – |
| G (GPa) | 123 | 59.5 | 64.7 | 46.6 | 73.78/– |
| Alloy | Concentrations (at.%) | Mo | Nb | Ta | V |
|---|---|---|---|---|---|
| MoNbTaV | 24.9 | 25.8 | 26.6 | 22.7 | |
| 27.6 | 25.0 | 31.5 | 15.9 | ||
| 19.6 | 27.5 | 19.0 | 33.9 |
| Alloy | (%) | (kJ/mol) | (JK−1·mol−1) | ∆χ | ||
|---|---|---|---|---|---|---|
| MoNbTaV | 3.59 | −3.25 | 11.53 | 9.86 | 5.25 | 0.26 |
| Mo | Nb | Ta | V | |
|---|---|---|---|---|
| Mo | 0 | −0.049/0.696 | −0.049/0.621 | 0.036/0.901 |
| Nb | 0.049/−0.696 | 0 | 0/−0.084 | 0.085/0.243 |
| Ta | 0.049/−0.621 | 0/0.084 | 0 | 0.085/0.325 |
| V | −0.036/−0.901 | −0.085/−0.243 | −0.085/−0.325 | 0 |
| Parameters | Mo | Nb | Ta | V |
|---|---|---|---|---|
| −0.019 | 0.035 | 0.035 | −0.058 | |
| 0.618 | −0.158 | −0.067 | −0.41 | |
| (MPa) | 647 | 302 | 273 | 631 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, H.; Qiao, J.-W.; Gao, M.C.; Hawk, J.A.; Ma, S.-G.; Zhou, H. MoNbTaV Medium-Entropy Alloy. Entropy 2016, 18, 189. https://doi.org/10.3390/e18050189
Yao H, Qiao J-W, Gao MC, Hawk JA, Ma S-G, Zhou H. MoNbTaV Medium-Entropy Alloy. Entropy. 2016; 18(5):189. https://doi.org/10.3390/e18050189
Chicago/Turabian StyleYao, Hongwei, Jun-Wei Qiao, Michael C. Gao, Jeffrey A. Hawk, Sheng-Guo Ma, and Hefeng Zhou. 2016. "MoNbTaV Medium-Entropy Alloy" Entropy 18, no. 5: 189. https://doi.org/10.3390/e18050189
APA StyleYao, H., Qiao, J.-W., Gao, M. C., Hawk, J. A., Ma, S.-G., & Zhou, H. (2016). MoNbTaV Medium-Entropy Alloy. Entropy, 18(5), 189. https://doi.org/10.3390/e18050189