Robust Estimation for the Single Index Model Using Pseudodistances
Abstract
:1. Introduction
2. The Single Index Model
3. Robust Estimators for the Single Index Model and Robust Portfolios
3.1. Definitions of the Estimators
3.2. Asymptotic Properties
3.2.1. Consistency
3.2.2. Asymptotic Normality
3.3. Influence Functions
3.4. Equivariance of the Regression Coefficients’ Estimators
3.5. Robust Portfolios Using Minimum Pseudodistance Estimators
4. Applications
4.1. Comparisons of the Minimum Pseudodistance Estimators with Other Robust Estimators for the Linear Regression Model
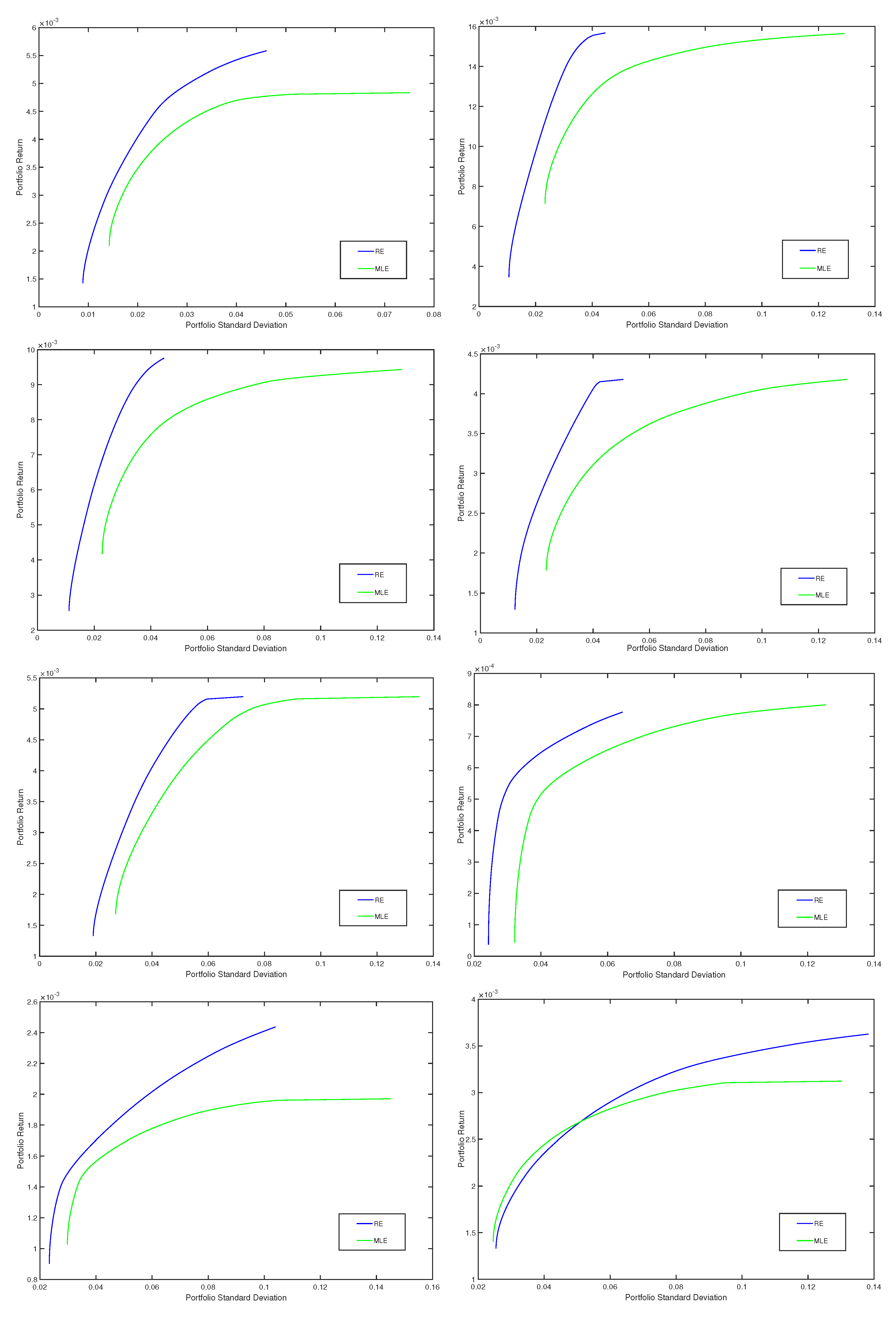
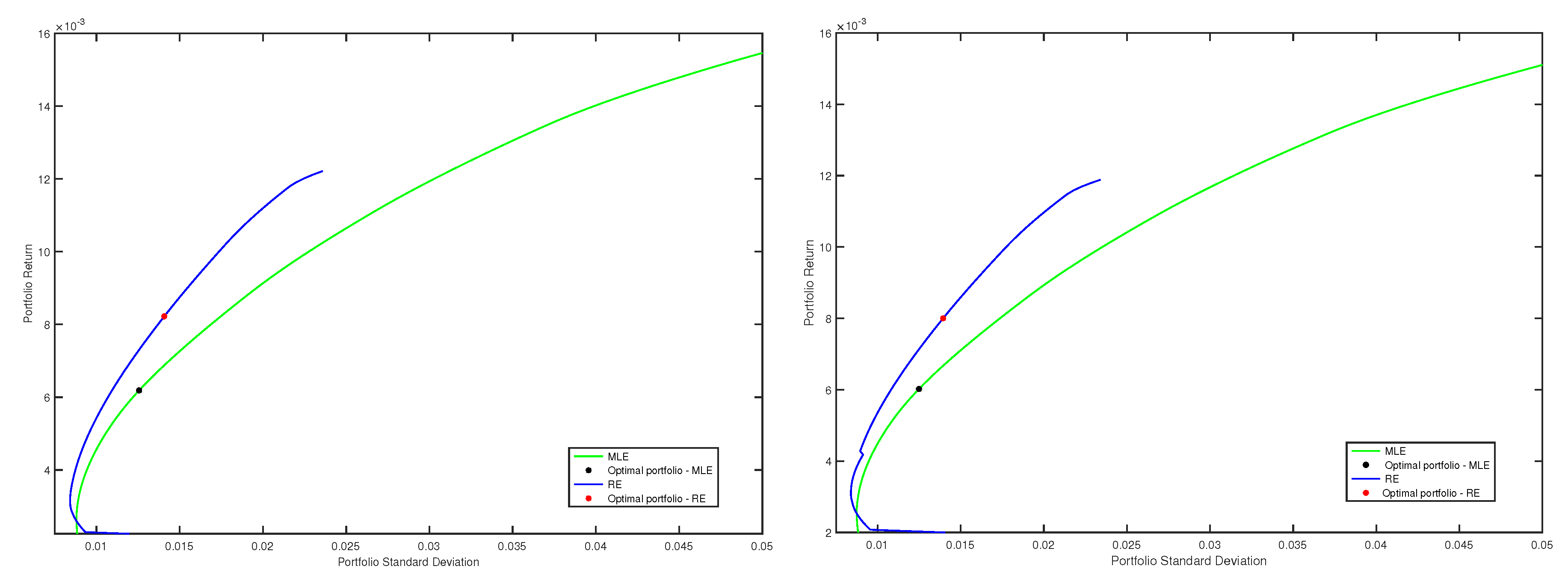
4.2. Robust Portfolios Using Minimum Pseudodistance Estimators
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Appendix A. Proof of the Results
Appendix B. The 50 Stocks and Their Abbreviations
- Asbury Automotive Group, Inc. (ABG)
- Arctic Cat Inc. (ACAT)
- American Eagle Outfitters, Inc. (AEO)
- AK Steel Holding Corporation (AKS)
- Albany Molecular Research, Inc. (AMRI)
- The Andersons, Inc. (ANDE)
- ARMOUR Residential REIT, Inc. (ARR)
- BJ’s Restaurants, Inc. (BJRI)
- Brooks Automation, Inc. (BRKS)
- Caleres, Inc. (CAL)
- Cincinnati Bell Inc. (CBB)
- Calgon Carbon Corporation (CCC)
- Coeur Mining, Inc. (CDE)
- Cohen & Steers, Inc. (CNS)
- Cray Inc. (CRAY)
- Cirrus Logic, Inc. (CRUS)
- Covenant Transportation Group, Inc. (CVTI)
- EarthLink Holdings Corp. (ELNK)
- Gray Television, Inc. (GTN)
- Triple-S Management Corporation (GTS)
- Getty Realty Corp. (GTY)
- Hecla Mining Company (HL)
- Harmonic Inc. (HLIT)
- Ligand Pharmaceuticals Incorporated (LGND)
- Louisiana-Pacific Corporation (LPX)
- Lattice Semiconductor Corporation (LSCC)
- ManTech International Corporation (MANT)
- MiMedx Group, Inc. (MDXG)
- Medifast, Inc. (MED)
- Mentor Graphics Corporation (MENT)
- Mistras Group, Inc. (MG)
- Mesa Laboratories, Inc. (MLAB)
- Meritor, Inc. (MTOR)
- Monster Worldwide, Inc. (MWW)
- Nektar Therapeutics (NKTR)
- Osiris Therapeutics, Inc. (OSIR)
- PennyMac Mortgage Investment Trust (PMT)
- Paratek Pharmaceuticals, Inc. (PRTK)
- Repligen Corporation (RGEN)
- Rigel Pharmaceuticals, Inc. (RIGL)
- Schnitzer Steel Industries, Inc. (SCHN)
- comScore, Inc. (SCOR)
- Safeguard Scientifics, Inc. (SFE)
- Silicon Graphics International (SGI)
- Sagent Pharmaceuticals, Inc. (SGNT)
- Semtech Corporation (SMTC)
- Sapiens International Corporation N.V. (SPNS)
- Sarepta Therapeutics, Inc. (SRPT)
- Take-Two Interactive Software, Inc. (TTWO)
- Park Sterling Corporation (PSTB)
References
- Sharpe, W.F. A simplified model to portfolio analysis. Manag. Sci. 1963, 9, 277–293. [Google Scholar] [CrossRef]
- Alexander, G.J.; Sharpe, W.F.; Bailey, J.V. Fundamentals of Investments; Prentice-Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Pardo, L. Statistical Inference Based on Divergence Measures; Chapman & Hall: Boca Raton, FL, USA, 2006. [Google Scholar]
- Basu, A.; Shioya, H.; Park, C. Statistical Inference: the Minimum Pseudodistance Approach; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Basu, A.; Harris, I.R.; Hjort, N.L.; Jones, M.C. Robust and efficient estimation by minimizing a density power divergence. Biometrika 1998, 85, 549–559. [Google Scholar] [CrossRef]
- Jones, M.C.; Hjort, N.L.; Harris, I.R.; Basu, A. A comparison of related density-based minimum divergence estimators. Biometrika 2001, 88, 865–873. [Google Scholar] [CrossRef]
- Broniatowski, M.; Keziou, A. Parametric estimation and tests through divergences and the duality technique. J. Multivar. Anal. 2009, 100, 16–36. [Google Scholar] [CrossRef]
- Toma, A.; Leoni-Aubin, S. Robust tests based on dual divergence estimators and saddlepoint approximations. J. Multivar. Anal. 2010, 101, 1143–1155. [Google Scholar] [CrossRef]
- Toma, A.; Broniatowski, M. Dual divergence estimators and tests: Robustness results. J. Multivar. Anal. 2011, 102, 20–36. [Google Scholar] [CrossRef]
- Fujisawa, H.; Eguchi, S. Robust parameter estimation with a small bias against heavy contamination. J. Multivar. Anal. 2008, 99, 2053–2081. [Google Scholar] [CrossRef]
- Broniatowski, M.; Vajda, I. Several applications of divergence criteria in continuous families. Kybernetica 2012, 48, 600–636. [Google Scholar]
- Broniatowski, M.; Toma, A.; Vajda, I. Decomposable pseudodistances and applications in statistical estimation. J. Stat. Plan. Inference 2012, 142, 2574–2585. [Google Scholar] [CrossRef]
- Markowitz, H.M. Mean-variance analysis in portfolio choice and capital markets. J. Finance 1952, 7, 77–91. [Google Scholar]
- Fabozzi, F.J.; Huang, D.; Zhou, G. Robust portfolios: contributions from operations research and finance. Ann. Oper. Res. 2010, 176, 191–220. [Google Scholar] [CrossRef]
- Vaz-de Melo, B.; Camara, R.P. Robust multivariate modeling in finance. Int. J. Manag. Finance 2005, 4, 12–23. [Google Scholar] [CrossRef]
- Perret-Gentil, C.; Victoria-Feser, M.P. Robust Mean-Variance Portfolio Selection. FAME Research Paper, No. 140. 2005. Available online: papers.ssrn.com/sol3/papers.cfm?abstract_id=721509 (accessed on 28 February 2018).
- Welsch, R.E.; Zhou, X. Application of robust statistics to asset allocation models. Revstat. Stat. J. 2007, 5, 97–114. [Google Scholar]
- DeMiguel, V.; Nogales, F.J. Portfolio selection with robust estimation. Oper. Res. 2009, 57, 560–577. [Google Scholar] [CrossRef]
- Toma, A.; Leoni-Aubin, S. Robust portfolio optimization using pseudodistances. PLoS ONE 2015, 10, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Toma, A.; Leoni-Aubin, S. Optimal robust M-estimators using Renyi pseudodistances. J. Multivar. Anal. 2013, 115, 359–373. [Google Scholar] [CrossRef]
- Van der Vaart, A. Asymptotic Statistics; Cambridge University Press: New York, NY, USA, 1998. [Google Scholar]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Andersen, R. Modern Methods for Robust Regression; SAGE Publications, Inc.: Los Angeles, CA, USA, 2008. [Google Scholar]
- Rousseeuw, P.J.; Yohai, V. Robust regression by means of S-estimators. In Robust and Nonlinear Time Series Analysis; Franke, J., Hardle, W., Martin, D., Eds.; Springer: New York, NY, USA, 1984; pp. 256–272. ISBN 978-0-387-96102-6. [Google Scholar]
- Ghosh, A.; Basu, A. Robust estimations for independent, non-homogeneous observations using density power divergence with applications to linear regression. Electron. J. Stat. 2013, 7, 2420–2456. [Google Scholar] [CrossRef]
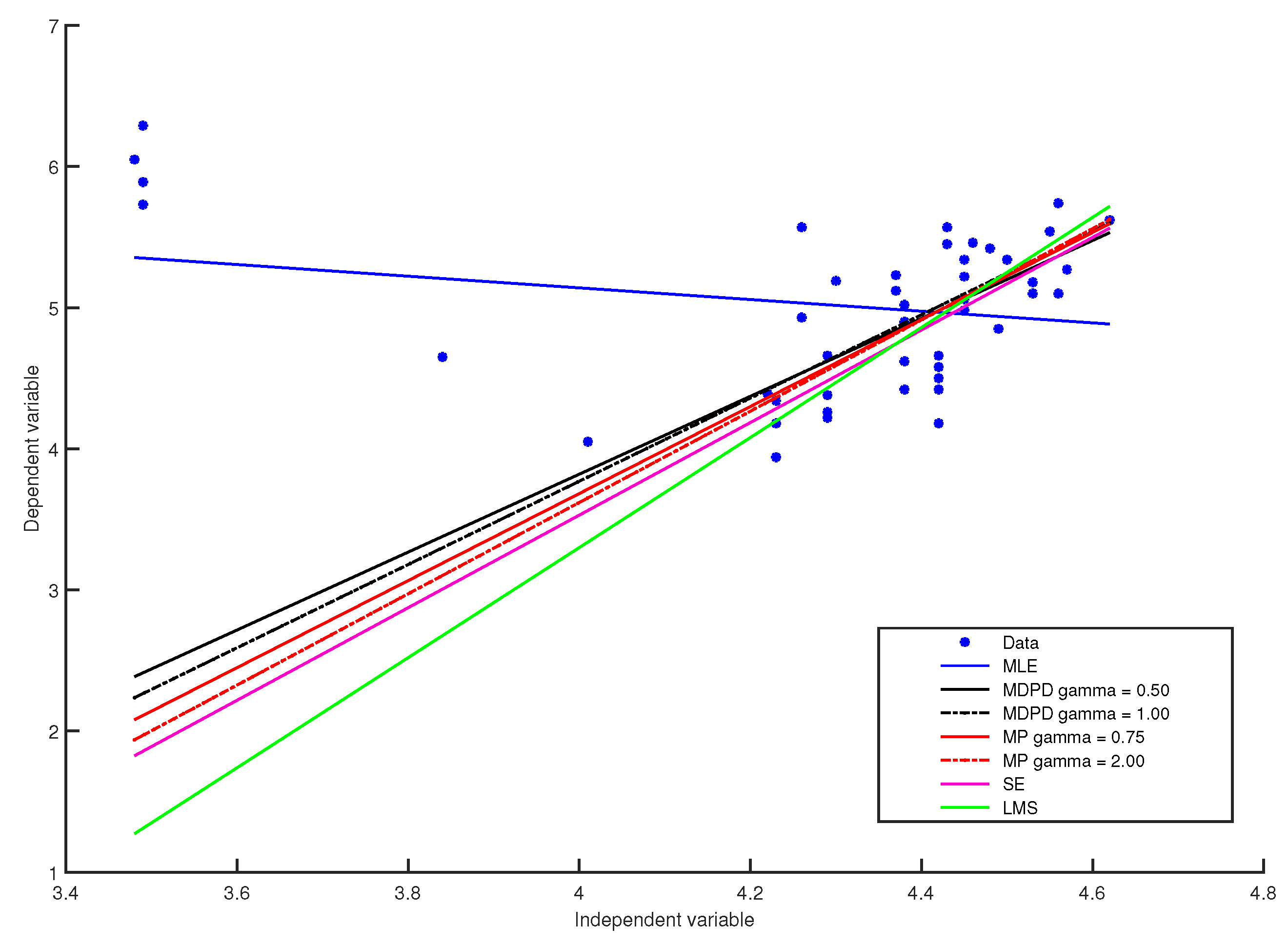
| MLE Estimates | |||
| 6.79 | −0.41 | 0.55 | |
| MP Estimates | |||
| 1 | |||
| 2 | |||
| MDPD Estimates | |||
| 1 | |||
| S-Estimates | |||
| − | |||
| LMS Estimates | |||
| − | |||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toma, A.; Fulga, C. Robust Estimation for the Single Index Model Using Pseudodistances. Entropy 2018, 20, 374. https://doi.org/10.3390/e20050374
Toma A, Fulga C. Robust Estimation for the Single Index Model Using Pseudodistances. Entropy. 2018; 20(5):374. https://doi.org/10.3390/e20050374
Chicago/Turabian StyleToma, Aida, and Cristinca Fulga. 2018. "Robust Estimation for the Single Index Model Using Pseudodistances" Entropy 20, no. 5: 374. https://doi.org/10.3390/e20050374
APA StyleToma, A., & Fulga, C. (2018). Robust Estimation for the Single Index Model Using Pseudodistances. Entropy, 20(5), 374. https://doi.org/10.3390/e20050374





