1. Introduction
Modern urbanization renders gas turbines to be a vital entity for power generation, aviation, and naval industries. Attributes including high efficiency, compact size, greater emissions compliance, wider fuel variability, flexibility in quicker ramp-up and shutdown, and cost-effectiveness help gas turbines to penetrate today’s market. On the other hand, the pursuit of higher reliability, availability, and sustainability demands modern gas turbines to incorporate advanced features [
1]. Among such features is the variable geometry in compressor and turbines that includes variable inlet guide vane (VIGV), variable stator vanes (VSVs), variable bleed valve (VBV), and variable area nozzle (VAN) [
2]. Variable guide vanes (VIGVs and VSVs) are made to function when the engine faces a speed fluctuation during startup, shutdown, and load change since they are scheduled as a function of spool speed [
3]. Often at low speed, during startup and shutdown, the engine may experience surging and stalling that can be harmful to the engine’s overall health and performance [
4]. Hence, the VIGVs and bleed control mechanism ensure stability and improve performance by alleviating surge in the axial compressor. In addition, the new generation of gas turbines face highly significant performance decline (deterioration) due to nonlinear and complex dynamics. Deterioration may also be triggered by some other factors such as malfunctions induced in the variable geometry mechanism, fouling in the axial compressor, and increased ambient temperature [
5].
The VIGVs are controlled by an actuating mechanism via different linkages connected to guide vanes [
6]. The VIVGs may encounter some malfunctions such as drifting of VIGVs away from the normal operational envelope. These malfunctions and faults lead to surging and choking in the compressor stages and eventually cause an accidental shutdown. Ishak and Ahmad [
7] categorized the common phenomena responsible for VIGV drift as (i) high-speed stop, (ii) low-speed stop, (iii) hydraulic ram leakage, and (iv) Rotary variable displacement transducer (RVDT) misalignment. Similarly, Tsalavoutas et al. [
8] stated that VIGVs are drifted outside from their normal schedule due to some other reasons: Wearing of actuation mechanism linkages and mispositioning/stacking of vanes due to loosed bolts. In order to avoid the occurrence of these faults, there is a need to continuously monitor and ensure that the movement and position of the actuation mechanism are synchronized with the actual design schedule. This approach; however, seems quite impractical as it is very hard to monitor the position of an actuation mechanism for a multiple numbers of vanes (in the case of vane stacking/loose bolt). Hence, Tsalavoutas et al. [
8] developed an adaptive performance model, initially suggested by Stamatis et al. [
9], to detect malfunctions in VIGVs. A few researchers have put forth efforts to observe the effect of VIGV drift on the performance of gas turbine by implanting some deliberate faults. Recently, Cruz-Manzo et al. [
10] developed a MATLAB Simulink-based performance model to examine the effect of implanted VIGV offset position angle on the performance of the compressor. The VIGV faults were indicated by a comparison of the offset between the VIGV position demanded and position given by the control system during operation. Similarly, Ishak and Ahmad [
7] developed a virtual sensor to predict the failure or malfunction of VIGVs. The fault was identified by comparing the deviation of the VIGV position given by the virtual sensor with the actual guide vane position from the control panel. Moreover, Razak et al. [
11] discussed the importance of the condition monitoring system to detect the VIGV malfunctions. Although a few researchers have analyzed the effect of VIGV drift on the performance of gas turbine through implanting deliberate faults, there has not been a study that simulates the real VIGV drift that engine faces during operation.
Gas turbines also face performance deterioration due to compressor fouling and increased inlet air temperature. Compressor fouling happens when sticky particulate matters get deposited on the compressor’s annulus passage including rotors and stators [
12]. Details on the effect of fouling on gas turbine performance can be found in [
13,
14,
15]. Adaptive performance models and simulations were conducted to predict the fouling rate with the passage of operating time to avoid severe performance deterioration. Qingcai et al. [
16] developed a genetic algorithm (GA)-based steady-state simulation model to analyse the effect of changing fouling parameters, mass flow, and isentropic efficiency on full- and part-load performance of a three-shaft industrial gas turbine. Similarly, Mohammadi and Montazteri-Gh [
17] developed a fault simulation model by implanting some faults signatures through changing compressor and turbine characteristics curves. Although many researchers have worked on the fouling, no study was reported in the literature related to fouling severity for a variable geometry gas turbine. High inlet air temperature also leads to performance deterioration in the gas turbine. Normally, hot climates face a temperature augmentation of around 10 °C above the design condition temperature (i.e., 15 °C) that leads to a power deterioration by around 7% [
18]. To avoid this power deterioration, inlet air cooling (IAC) is a commercially employed technique that reduces the temperature of the intake air to the compressor [
19]. A variety of techniques were employed in the literature for IAC for industrial gas turbines, as discussed by Bakeem et al. [
20]. Although a variety of pertinent literature exists in [
21,
22,
23,
24,
25] regarding the IAC technique, to the authors’ knowledge, there is no evidence of any investigation of the effect of IAC on the performance and performance degradation characteristics of variable geometry industrial gas turbines.
The VIGV drift and fouling generally depict similar behavior by reducing the annular flow passage of the compressor, consequently, causing the overall performance deterioration and compressor failure due to surging. Hence, it is a hard task to identify the root cause of the performance degradation and surging, which can be either VIGV drift or fouling. After a detailed study of the literature, it has become evident that the VIGV drift has remained barely studied. Although some researchers [
8] have worked on it, their work focused on implanted VIGV drift faults. Besides, the effect of the real time VIGV drift that an engine faces during operation (i.e., incorporating the minimum and maximum limits of drift offset ranging from −6.5° to +6.5°, respectively) has not been simulated. Moreover, fouling and IAC have not been studied for a variable geometry gas turbine. The combined effect of VIGV drift, fouling, and IAC has also remained unexplored.
In the present study, the combined effect of VIGV drift, compressor fouling, and increased ambient temperature on gas turbine performance were investigated. A steady-state simulation model for a three-shaft gas turbine (GE LM1600) was developed using a commercial software, GasTurb 12. Firstly, the effect of VIGV drift was simulated by running the off-design steady-state model on three different variable geometry schedules: (i) up-drift schedule (off-set of +6.5° from Muir [
26]), (ii) normal schedule (Muir schedule [
26]), and (iii) down-drift schedule (off-set of −6.5° from Muir [
26]). Secondly, a parametric study was conducted to simulate the effect of increased ambient temperature on the performance of the targeted engine. IAC was envisaged by a designated temperature (T = 265 K). Finally, the effect of compressor fouling on the performance of the gas turbine was simulated by using the modifier module available in the gas turbine.
2. Thermodynamic Model
2.1. Model Inputs and Physical Properties
The focus for the present paper was a three-shaft industrial gas turbine. Accordingly, we selected LM1600 engine since it involves variable geometry inlet guide vanes and its design is similar to other gas turbines like Rolls-Royce RB211 and MT30 engines. General Electric LM1600 engine is featured by ISO power rating of 13.7 MW with 50 Hz generator frequency, a low pressure (LP) spool, a concentric high pressure (HP) spool, and an aerodynamically coupled power turbine. The VIGV is installed at the low pressure compressor. The engine is typically utilized for power generation and mechanical drive applications in the oil and gas industry. The basic technical data needed for modeling the gas turbine are listed in
Table 1.
In most cases, the thermodynamic processes involved in a gas turbine, such as compression, combustion, and expansion, are assumed to be ideal and the working fluid properties (specific heat
Cp and isentropic index γ) are also considered constant. However, practically, these assumptions are not valid as the specific heat of the working fluid (i.e., air) varies with respect to temperature in the real process [
27]. In addition, during combustion, air is converted into gaseous products having different composition that can affect the
Cp and γ. Hence, GasTurb 12 considers the working fluid as a semi-ideal gas and the specific heats of air and the gaseous products to vary with temperature as given in Equations (1) and (2) [
27,
28].
where
,
,
and
are the specific heat values estimated from Equation (1) using the values of the coefficients
A,
B, and
C from
Table 2.
2.2. Design Point Calculations
Design point calculation is a basic step during the performance evaluation of any gas turbine, because it helps in finding the unknown design parameters using thermodynamic and compatibility equations. This calculation requires the inherent design characteristics of a specific engine to be re-established. However, due to the scarcity of data and very limited information made public through literature or via product brochures, some empirical assumptions and engineering judgments were required, as given in
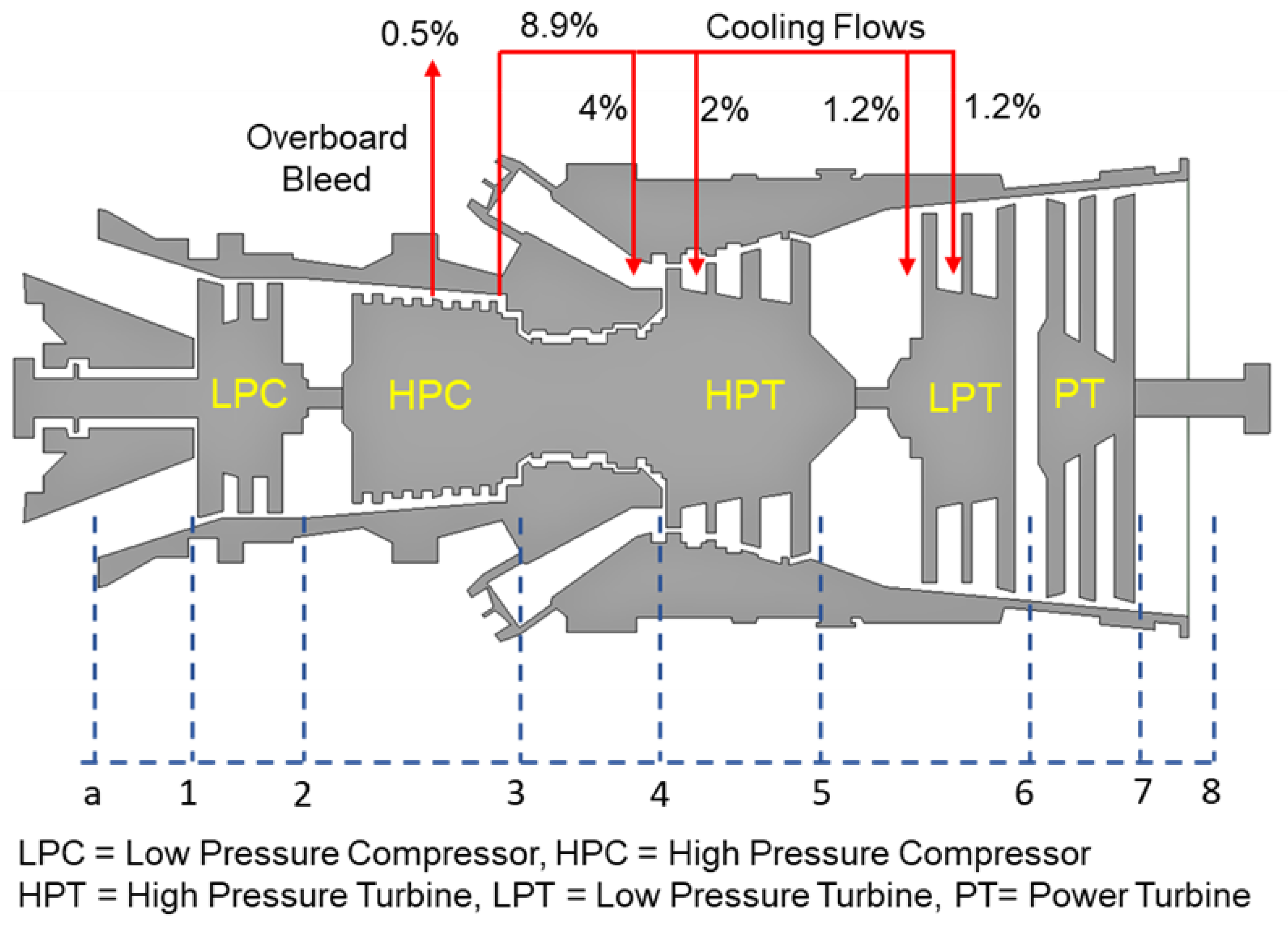
Table 3. The power rating and spool speeds are in accordance with the information in the gas turbine product catalog and the ambient conditions data are based on the international organization for standardization (ISO) design point standards. The overall thermodynamic modeling of a gas turbine is often established through individual component-based modeling. GasTurb 12 also works on the same principle of component-based modeling. Generally, a three-shaft gas turbine is comprised of eight major components: Inlet duct, low-pressure compressor (LPC), high-pressure compressor (HPC), combustor, high-pressure turbine (HPT), low-pressure turbine (LPT), free power turbine (FPT), and an exhaust duct at the end. These components were; thus, modeled exclusively during design point by utilizing input parameters values that were provided by the manufacturer and some assumed values. In addition, GasTurb 12 also requires secondary air flows data: turbine cooling bleed and overboard bleed flow data [
29]. In the present study; however, the HPT and LPT were cooled with bleed extracted from downstream of HPC, as shown in
Figure 1.
The individual gas turbine components are generally modeled using physical- and thermodynamic-based equations. In addition, component characteristics maps are utilized to find the values of the mass flow, pressure ratio, and efficiency of the compressor and turbine. Once the inlet conditions (ma, Ta, Pa) and fuel flow are known, the unknown parameters can be found at every station using thermodynamic equations. The component-wise thermodynamic equations needed for modeling are discussed below.
For inlet duct, the pressure loss is accounted as follows:
For the LP compressor, with known inlet conditions (
T1,
P1) and a given compressor map, the exit conditions (
T2, P2, Wc, m2) can be easily estimated. The outlet temperature (
T2) is calculated using the specific entropy correlation in Equation (4) to account for the effect of temperature on the specific heat of the working fluid.
The compressor power consumption can be estimated by the following expressions:
where the values of
ηlpc and
PRlpc can be determined from the specific compressor map at a certain shaft speed
N. Similarly, for HPC, the modeling equations are as follows:
Th combustion chamber is modeled using the simplified energy balance equation and pressure loss expression. Assuming the value of combustion efficiency, the temperature
T4 can be estimated as follows:
The HPT can also be modeled in the same fashion as the compressor:
For the free power turbine, the same steps are repeated as follows:
These design point calculations results were compared with results from a previous research conducted by Zhu and Saravanamuttoo [
30] and data from the gas turbine product catalog. As far as credibility goes, the product catalog data is considered more reliable. Hence, both simulations results (i.e., from Zhu and Saravanamuttoo [
30] and from the GasTurb 12 in the present study) were validated against the product catalogue data. As presented in
Table 4, the percent error in estimated power output and exhaust temperature from the Zhu and Saravanamuttoo study showed significantly high deviation from the catalog data. On the contrary, the percent errors calculated for the results from GasTurb 12 in the present study showed only a very minute deviation from the catalogue data. Therefore, it was concluded that design point results generated through GasTurb 12 simulation are considered more reliable because they are meeting the actual design norms by showing less deviation.
Once the cycle design point calculations were accurately estimated in GasTurb 12, suitable compressor and turbine performance maps were then selected. Following that, a parametric study on the effect of the ambient inlet air temperature (Tamb) was performed in the range 265–315 K with an interval of 5 K. The temperature range was segregated into three scenarios: (i) Inlet air cooled temperature (Tamb = 265 K), (ii) near design point temperature (Tamb = 290 K), and (iii) hot day temperature (Tamb = 315 K). After setting these temperature ranges as an input to the simulation program, the off-design performance simulations were tracked.
2.3. Off-Design Simulations
During off-design simulations, the GasTurb 12 performs two major tasks: (i) Adaptation of the design point of the target engine with already known compressor and turbine maps using scaling method; and (ii) component matching by guaranteeing the compatibility of mass flow and work using Newton-Raphson iterative algorithm [
29,
31]. For compressor map adaptations, a suitable characteristics map with design point data was selected and then it was digitized in a form of a lookup table and finally exit calculations were performed. Auxiliary coordinate,
β, was incorporated in the compressor map digitization process to avoid discrepancy as suggested by Kurzke [
32]. After the inclusion of
β coordinates, compressor characteristics were embodied as the following functions,
where,
Neverthless, due to unavailability of compressor maps in the literature, scaling was performed to make the design point of the desired engine to be in accordance with the design of the original compressor. GasTurb 12 utilizes the same scaling factors introduced by Sellers and Deniel [
33], as given in Equations (32)–(34).
Component matching of all the components of a gas turbine is indispensable because it helps in estimating an optimized overall performance of the system at a specified ambient condition. In GasTurb 12, the components are matched by ensuring the compatibility of flow and work between the interconnected individual components. Hence, to develop a steady-state off-design operating line, the Newton-Raphson iterative algorithm was employed due to its inherent efficiency in numerical solution and ease of applicability to non-linear systems [
29]. In the present study, seven iteration variables (
βLPC, βHPC, TIT, βHPT, βLPT, βFPT, %NFPT) and seven errors were used to carry out the off-design calculation. The schematic diagram for component matching using Newton-Raphson method is shown in
Figure 2. Mass flow and work compatibility equations are given in Equations (35)–(41).
The combustor section,
The HP turbine section,
The LP turbine section,
Apart from this, work compatibility between the components were ensured as follows:
For HP spool,
The LP spool,
The power turbine spool,
2.4. Variable Inlet Guide Vane Drift Simulations
In general, faults associated with the variable geometry mechanism of the compressor are hard to detect during real-time system operation. As an alternative, some faults were implanted deliberately in order to observe the effects of these unforeseen faults on the severity of overall gas turbine’s performance deterioration. To investigate the effect of VIGV drift, a VIGV schedule suggested by Muir et al. [
26] was considered as the benchmark and standard schedule for the present study. Drift in the variable geometry mechanism occurs typically when one or more of the guide vanes are not moving according to the schedule provided by the gas turbine control system, as shown in
Figure 3. Occasionally, failure in some bolts or wearing of the links in the VIGV mechanism can also lead to a drift. That is the reason why the guide vanes that do not follow the control schedule are termed as mis-scheduled or drifted outside the normal schedule.
In GasTurb 12, the variable guide vane drift were simulated by incorporating the VIGV schedule as an input command during the off-design simulation phase. These simulations were carried out for three different VIGV schedules: (i) down-drift schedule, (ii) normal schedule, and (iii) up-drift schedule. The schedules were established by featuring a ± 6.5° angle offset margin from the optimum schedule of Muir et al. [
26]. The offset margin of
θVIGV = −6.5° was termed as the down-drift schedule, while
θVIGV = +6.5° was named as up-drift from the Muir’s schedule. The reason for developing these two offset margins in the VIGV schedule was due to the fact that during real-time operation the gas turbine may approach these two limits: the maximum limit (+6.5°) and the minimum limit (−6.5°). The three variable guide vane schedules as a function of percent spool speed are shown in
Figure 4.
Design point calculations in GasTurb 12 assumes a fixed geometry (
θVIGV = 0°) compressor. To establish the off-design steady-state simulations, a VIGV schedule needs to be selected according to the configuration of the engine. The VIGV feature in GasTurb 12 is activated by assuming some suitable values for the correction factors,
,
, and
, as given in Equations (41)–(44). Every 1° change in VIGV angle results in a 1% variation in the mass flow and pressure ratio. So an appropriate value of
is always needed [
28].
The correction factor required for efficiency in GasTurb 12 is done by changing the
factor in the equation given below (Equation (45)). It became evident from a number of simulations that efficiency decreases by fraction of 0.01 for every ±10° modulation in
setting, whereas a ±15° variation in the angle reduces efficiency by 0.0225 [
28]. Hence, the assumed values
= = 1 and
= 0.01 are kept constant as an input wherever more information about the compressor is not available, and this assumption also avoids excessive efficiency loss [
28,
29].
In the present study, the variable guide vanes were considered for low pressure compressor as per the available specifications for LM1600 engine. The effect of performance deterioration was evident from compressor characteristics maps, as discussed in the following sections.
2.5. Effect of Inlet Air Temperature
The effect of inlet air cooling was also accounted in the parametric study by designating a temperature of T = 265 K as the temperature after integrating the gas turbine system with inlet air cooling mechanism. However, there was no such physical or thermodynamic connection of IAC system with the studied gas turbine, rather IAC was visualized by setting a temperature of 265 K as the inlet cooled temperature in the parametric study. The details of the study are mentioned in the following sections.
2.6. Simulating the Effect of Fouling
Other phenomena that may lead to performance deterioration in a gas turbine include fouling, erosion, corrosion, and foreign object damage (FOD) in the compressor and turbine sections. In this study, fouling in the compressor was taken into consideration. Compressor fouling takes place when some contaminated particles adhere to the surface of the blades and the annulus flow passage. The aerodynamic behavior may change due to the decreased flow passage owing to the particulate deposits. Compressor fouling can lead to (i) mass flow reduction, (ii) loss of pressure ratio and efficiency, (iii) increased heat rate, (iv) increased specific fuel consumption, and (v) reduced surge margin.
Compressor fouling was simulated in the GasTurb 12 using the
Modifier option available in the software. Physical faults in the gas turbine were quantified by the change in the various independent parameters (i.e., isentropic efficiency, flow capacity, NGV area, and combustion efficiency etc.) that describe component performance. This change in the independent parameters then leads to deviation in the dependent parameters such as temperature, pressure, power output, and fuel flow. In the present study, change in the compressor isentropic efficiency
(∆ηc) and flow capacity
(∆Γ
c) (independent parameters) were considered to quantify the fouling phenomena in the compressor. Escher et al. [
34] developed some correlations between the physical faults and the independent parameters. According to these correlations, for every 1% decrease in the compressor isentropic efficiency, the mass flow decreases by 3%. It is worth mentioning that the maximum interval limits for efficiency variation are 0% and −2.5%, while for compressor flow capacity it is 0% and −7.5%, maintaining a ratio of 1:3. To simulate the deterioration model, component characteristics maps need to be updated to accommodate for the deterioration. However, the maps already stored in the simulation program are for a clean engine. Thus, for a deteriorated engine the scaling factors of the compressor map need to be updated according to the variation of the independent parameters. The scaling factors for mass flow, isentropic efficiency, and pressure ratio as suggested by Qingcai et al. [
16] are given below.
2.7. Effect of Fouling and VIGV Drift on Physical Parameters
Incipient faults in a gas turbine are generally traced using carefully selected indicators, which are based on the variations in the values of the dependent parameters. Dependent parameters are those that are measurable with the help of sensors at specific stations in the gas turbine. Pressure, temperature, fuel flow, and power output are considered dependent parameters. In case of any physical faults such as fouling, erosion and corrosion, or any malfunction (e.g., VIGV drift), these physical parameters are altered. A detailed comparison of all the physical parameters at every stage in the gas turbine is shown in
Table 5. Fouling displayed a significant effect and hence it was quantified at two different severity levels: 0% and 100%. In addition, fouling was evaluated at three different schedules. With the increase in the fouling severity level, the mass flow and pressure showed a significant decrease at every station, while the temperature increased. The percent variation of pressure between the clean condition and fully deteriorated condition at the down-drift schedule was comparatively lower than the other two schedules. Similarly, the percent deviations for temperature at Muir’s schedule and the up-drift schedule were comparatively higher than at the down-drift schedule. It was inferred from this comparison that the Muir’s and the up-drift schedules were more vulnerable to fouling as compared to the down-drift schedule. The comparison in the table suggests that in the case of simultaneous fouling and VIGV drift, the probability of failure would be more at the VIGV up-drift and Muir’s schedule. Hence, the VIGV down drift was proved to be a good schedule in order to avoid failure due to fouling and VIGV drift. Moreover, this analysis of physical parameters at each station can be used for effective fault detection and diagnostics during the combined failure mode.
4. Conclusions
In the present study, modeling and steady-state off-design simulation were performed for a three-shaft industrial gas turbine (aeroderivative gas turbine, GE LM1600) to investigate the combined effect of VIGV drift, fouling, and inlet air cooling on the overall performance of the engine. The simulation model was developed with the help of a commercially available software GasTurb 12. VIGV drift was simulated by considering two different schedules deviating from the normal schedule that was adopted from Muir study. Apart from this, fouling was simulated by running the simulation model of 11 different fouling severity levels from 0% to 100%. These fouling severity levels were incorporated by two independent health parameters (i.e., change in compressor flow capacity and change in compressor isentropic efficiency). With increasing levels of fouling severity, the performance parameters showed a significant deterioration. However, combining the VIGV down-drift schedule resulted in increased power output, thermal efficiency, and surge margin by 14.53%, 5.55%, and 32.08%, respectively. Similarly, SFC was also decreased by 5.23% at VIGV down-drift schedule. In addition, a parametric study was conducted in order to see the effect of increased inlet air temperature on the performance. During parametric study, three temperature settings were defined to indicate different ambient condition. It became evident that, with increased temperature (T = 315 K) and increased fouling severity level, the overall performance deteriorated rigorously. Consequently, the down-drift schedule helped in managing the performance to an improved level. A temperature of T = 265 K was considered as inlet air cooled temperature, obtained right after the integration of gas turbine inlet with an inlet air cooling mechanism. The integration of the inlet air cooling technique helped to improve the power output, thermal efficiency, surge margin, and SFC by 29.67%, 7.38%, 32.84%, and 6.88%, respectively. The simulation results revealed that the VIGV down-drift can compensate the effect of performance deterioration and compressor surge due to fouling and helps in improving the performance.
The results from the developed model can serve as a basis for acquiring insights related to gas turbine fault detection and diagnostics (FDDs). Moreover, it also help in troubleshooting the root cause of the performance degradation and compressor surge in an engine faced with a VIGV drift and fouling simultaneously.