An Entropy-Based Neighborhood Rough Set and PSO-SVRM Model for Fatigue Life Prediction of Titanium Alloy Welded Joints
Abstract
:1. Introduction
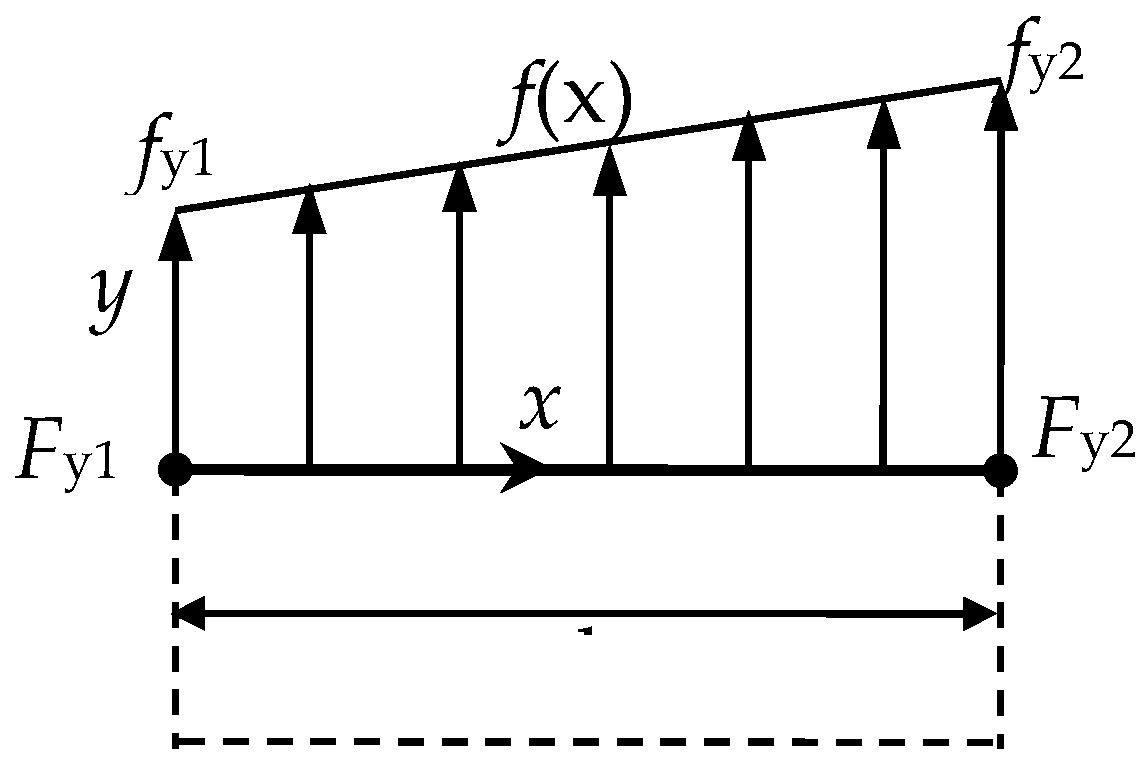
2. Nodal Force Based Structural Stress Principle
3. Entropy Based Neighborhood Rough Set Model
3.1. Basic Concept
- (1)
- ;
- (2)
- , if and only ifx = y;
- (3)
- ;
- (4)
- .
3.2. Entropy-Based Neighborhood Reduction Algorithm
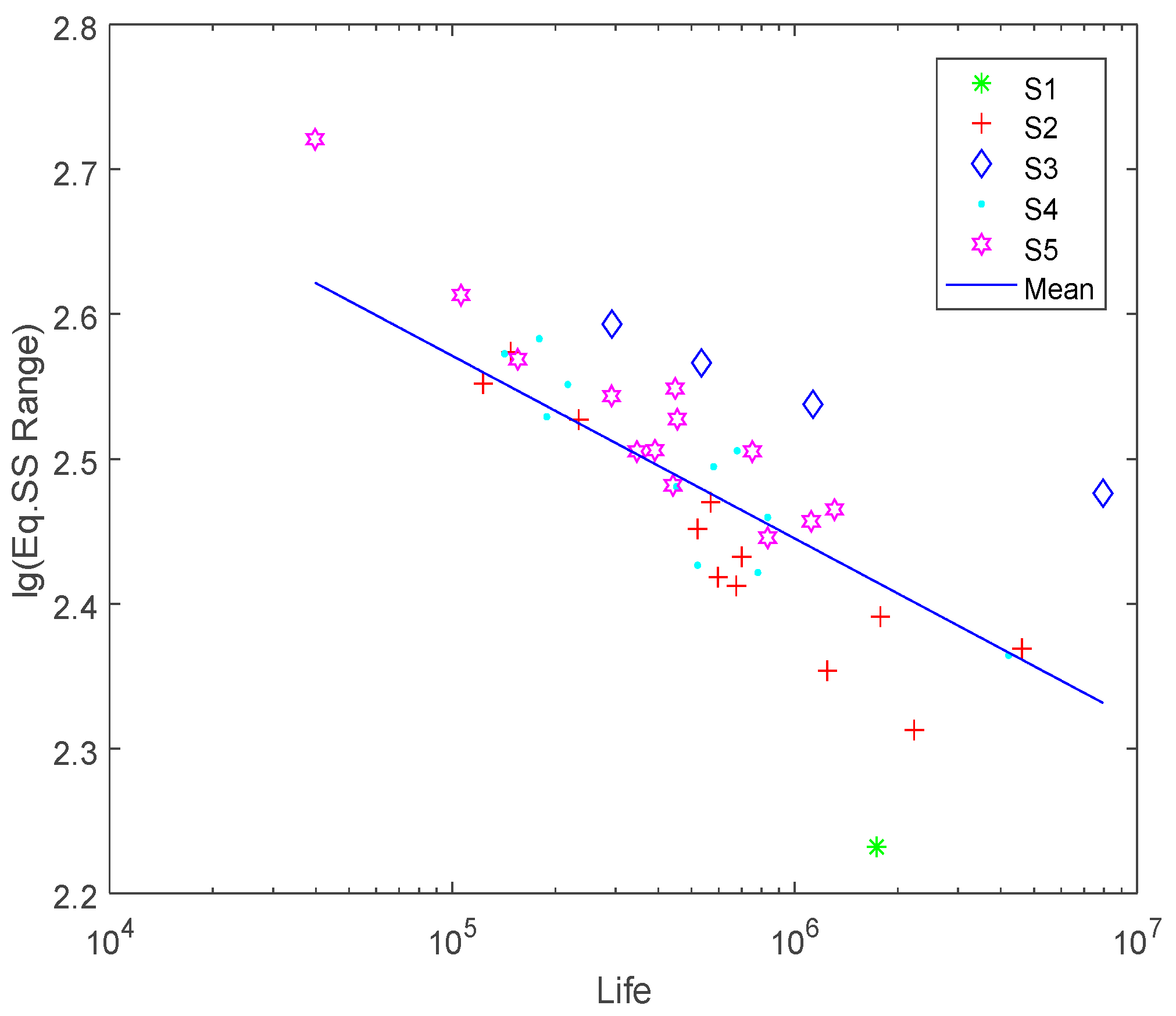
3.3. Fatigue Characteristic Domain Determination
4. PSO-SVRM Model for Fatigue Life Prediction of Titanium Alloy Welded Joints
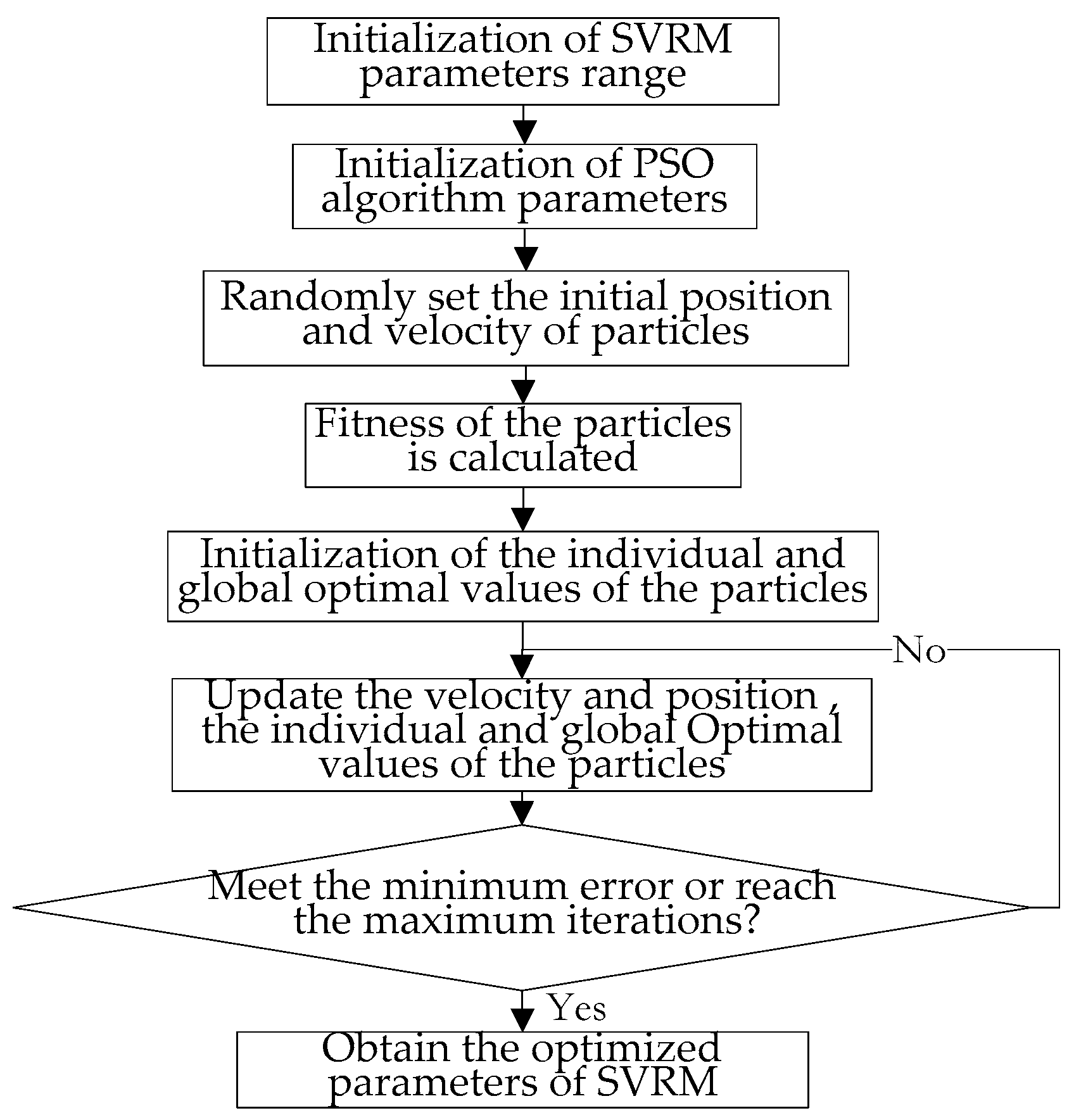
4.1. PSO Algorithm
4.2. SVRM Principle
4.3. PSO-SVRM Model
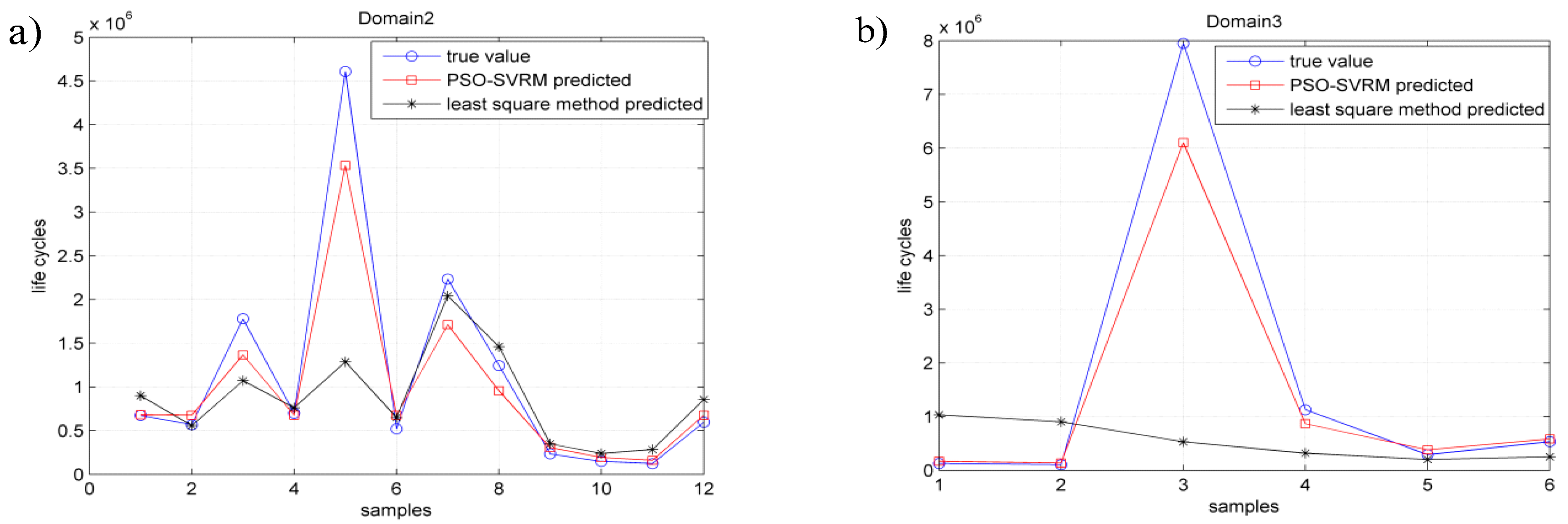
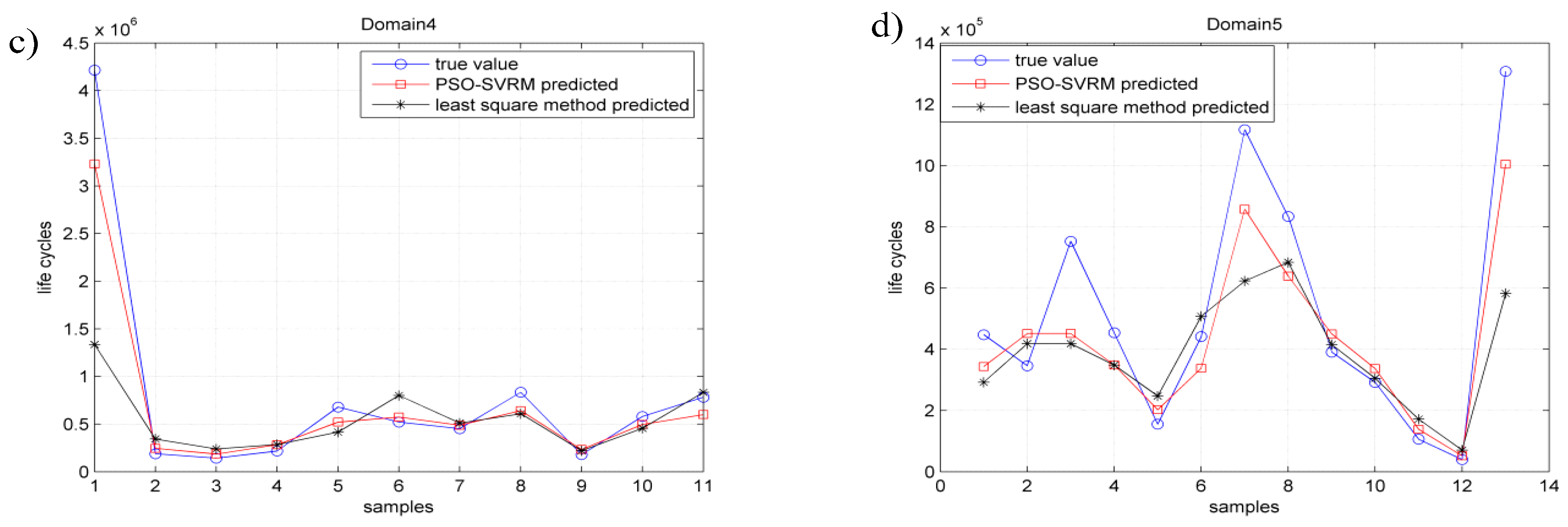
5. Results and Discussions
6. Conclusions
- (1)
- The reduction results show that besides the equivalent structural stress range, the joint type influencing factors also play a very important role in determining the fatigue life of titanium alloy welded joints.
- (2)
- The fatigue characteristic domain could be determined according to the reduction results of the entropy-based neighborhood rough set theory.
- (3)
- A PSO-SVRM model for fatigue life prediction of titanium alloy welded joints is established in the determined fatigue characteristic domain. Experimental results indicate that compared with the traditional least squares method, the proposed PSO-SVRM model could better predict the fatigue life of the titanium alloy welded joints.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Appendix A.1. Entropy-Based Neighborhood Reduction Algorithm Consists of five Main Steps
Appendix A.2. The PSO-SVRM Model for Fatigue Life Prediction of Welded Joints Within the Defined Fatigue Characteristics Domains Includes
References
- Hobbacher, A. Recommendations for Fatigue Design of Welded Joints and Components, 2nd ed.; Springer: Cham, Switzerland, 2016; pp. 91–105. ISBN 978-3-319-23756-5. [Google Scholar]
- Fricke, W. Fatigue analysis of welded joints state of development. Mar. Struct. 2003, 16, 185–200. [Google Scholar] [CrossRef]
- Niemi, E. On the Determination of Hot Spot Stresses in the Vicinity of Edge Gussets; Department of Mechanical Engineering, Lappeenranta University of Technology: Lappeenranta, Finland, 1994; Volume 18. [Google Scholar]
- Niemi, E.; Tanskanen, P. Hot spot stress determination for welded edge gussets. Weld. World 2000, 44, 31–37. [Google Scholar]
- Dong, P. A structural stress definition and numerical implementation for fatigue analysis of welded joints. Int. J. Fatigue 2001, 23, 865–876. [Google Scholar] [CrossRef]
- Dong, P.; Hong, J.K. The Master S-N curve approach to fatigue of piping and vessel welds. Weld. World 2004, 48, 28–36. [Google Scholar] [CrossRef]
- Dong, P.; Prager, M. The Design Master S-N Curve in ASME Div 2 Rewrite and its Validations. Weld. World 2007, 51, 53–63. [Google Scholar] [CrossRef]
- Basaran, C.; Yan, C.Y. A Thermodynamic Framework for Damage Mechanics of Solder Joints. Trans. ASME J. Electron. Packag. 1998, 20, 379–384. [Google Scholar] [CrossRef]
- Basaran, C.; Nie, S. An Irreversible Thermodynamic Theory for Damage Mechanics of Solids. Int. J. Damage Mech. 2004, 13, 205–224. [Google Scholar] [CrossRef]
- Leonid, S.; Sergei, S. Mechanothermodynamic Entropy and Analysis of Damage State of Complex Systems. Entropy 2016, 18, 268. [Google Scholar] [CrossRef]
- Zhang, M.; Shen, X.; He, L.; Zhang, K. Application of Differential Entropy in Characterizing the Deformation Inhomogeneity and Life Prediction of Low-Cycle Fatigue of Metals. Materials 2018, 11, 1917. [Google Scholar] [CrossRef] [PubMed]
- Basaran, C.; Tang, H. Implementation of a Thermodynamic Framework for Damage Mechanics of Solder Interconnects in Microelectronic Packaging. Int. J. Damage Mech. 2002, 11, 87–108. [Google Scholar] [CrossRef]
- Gomez, J.; Basaran, C. A Thermodynamics Based Damage Mechanics Constitutive Model for Low Cycle Fatigue Analysis of Microelectronics Solder Joints Incorporating Size Effect. Int. J. Solids Struct. 2005, 42, 3744–3772. [Google Scholar] [CrossRef]
- Naberi, M.; Amiri, M.; Khonsari, M. On the thermodynamic entropy of fatigue fracture. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2009, 466, 423–438. [Google Scholar] [CrossRef]
- Naberi, M.; Khonsari, M. Real-time fatigue life monitoring based on thermodynamic entropy. Struct. Health Monit. 2011, 10, 189–197. [Google Scholar] [CrossRef]
- Liu, Y.; Zou, L.; Sun, Y.; Yang, X. Evaluation Model of Aluminum Alloy Welded Joint Low-Cycle Fatigue Data Based on Information Entropy. Entropy 2017, 19, 37. [Google Scholar] [CrossRef]
- ASME. 2007 ASME Boiler and Pressure Vessel Code Section VIII Division 2 Part 5: Design by Analysis Requirement; The American Society of Mechanical Engineers: New York, NY, USA, 2007. [Google Scholar]
- Pawlak, Z. Roughclassification. Int. J. Man-Mach. Stud. 1984, 51, 469–483. [Google Scholar] [CrossRef]
- Lin, T.Y. Granular computing on binary relations. In Proceedings of the 3rd International Conference, Rough Sets and Current Trends in Computing, Malvern, PA, USA, 14–16 October 2002; pp. 296–299. [Google Scholar]
- Hu, Q.; Yu, D. Neighborhood rough set based heterogeneous feature subset selection. Inf. Sci. 2008, 178, 3577–3594. [Google Scholar] [CrossRef]
- Chen, Y.M.; Xue, Y.; Ma, Y.; Xu, F.F. Measures of uncertainty for neighborhood rough set. Knowl. Based Syst. 2017, 120, 226–235. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, K.; Chen, X. An entropy based uncertainty measurement approach in neighborhood rough set theory. Inf. Sci. 2014, 279, 239–250. [Google Scholar] [CrossRef]
- Dai, J.H.; Huang, D.B.; Su, H.S.; Tian, H.W.; Yang, T. Uncertainty measurement for covering rough sets. Int. J. Uncertain. Fuzz. Knowl. Based Syst. 2014, 22, 217–233. [Google Scholar] [CrossRef]
- Huang, B.; Guo, C.X.; Li, H.X.; Feng, G.F.; Zhou, X.Z. An intuitionistic fuzzy graded covering rough set. Knowl. Based Syst. 2016, 107, 155–178. [Google Scholar] [CrossRef]
- Iwata, T.; Matsuoka, K. Fatigue strength of CP Grade 2 Titanium fillet welded joint for ship structure. Weld. World 2004, 48, 40–47. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the 1995 IEEE International Conference, Neural Networks, Perth, Australia, 27 November 2011; pp. 1942–1948. [Google Scholar]
- Chan, F.; Tiwari, M. Swarm Intelligence: Focus on Ant and Particle Swarm Optimization. I-Tech Educ. Publ. 2007, 1, 114–115. [Google Scholar]
- Clerc, M.; Kennedy, J. The particle swarm: Explosion, stability, and convergence in a multi-dimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
- Vapnik, V. SVM method of estimating density, conditional probability, and conditional density. ISCAS 2000, 2, 749–752. [Google Scholar]
- Yan, M.; Wang, J. Classification Algorithm of Regression Support Vector Machine and its Application to Environment Monitoring in Water Culture Plants. Appl. Mech. Mater. 2013, 427–429, 1121–1127. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Q. An Improved Extension Method of EMD Based on SVRM. Appl. Mech. Mater. 2014, 543–547, 2697–2701. [Google Scholar] [CrossRef]
- Deng, W.; Yao, R.; Zhao, H.; Yang, X.; Li, G. A novel intelligent diagnosis method using optimal LS-SVM with improved PSO algorithm. Soft Comput. 2017. [Google Scholar] [CrossRef]
- Deng, W.; Zhao, H.; Yang, X.; Xiong, J.; Sun, M.; Li, B. Study on an improved adaptive PSO algorithm for solving multi-objective gate assignment. Appl. Soft. Comput. 2017, 59, 288–302. [Google Scholar] [CrossRef]
- LIBSVM—A Library for Support Vector Machines. Available online: https://www.csie.ntu.edu.tw/~cjlin/libsvm/ (accessed on 7 December 2017).


| U | J | t (mm) | r | M | N (Cycles) | |
|---|---|---|---|---|---|---|
| x1 | LB | 2 | 0 | JIS H4600 | 170.61 | 1734430 |
| x2 | LT | 2 | 0 | JIS H4600 | 258.4 | 675006 |
| x3 | CB | 2 | 0 | JIS H4600 | 248.51 | 129860 |
| x4 | LL | 2 | 0 | JIS H4600 | 353.73 | 447552 |
| x5 | LT | 10 | 0 | JIS H4600 | 205.54 | 2233310 |
| x6 | CB | 10 | 0 | JIS H4600 | 299.43 | 7946640 |
| x7 | CT | 10 | 0 | JIS H4600 | 288.15 | 833690 |
| x8 | LL | 10 | 0 | JIS H4600 | 278.98 | 833690 |
| ...... | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, L.; Sun, Y.; Yang, X. An Entropy-Based Neighborhood Rough Set and PSO-SVRM Model for Fatigue Life Prediction of Titanium Alloy Welded Joints. Entropy 2019, 21, 117. https://doi.org/10.3390/e21020117
Zou L, Sun Y, Yang X. An Entropy-Based Neighborhood Rough Set and PSO-SVRM Model for Fatigue Life Prediction of Titanium Alloy Welded Joints. Entropy. 2019; 21(2):117. https://doi.org/10.3390/e21020117
Chicago/Turabian StyleZou, Li, Yibo Sun, and Xinhua Yang. 2019. "An Entropy-Based Neighborhood Rough Set and PSO-SVRM Model for Fatigue Life Prediction of Titanium Alloy Welded Joints" Entropy 21, no. 2: 117. https://doi.org/10.3390/e21020117
APA StyleZou, L., Sun, Y., & Yang, X. (2019). An Entropy-Based Neighborhood Rough Set and PSO-SVRM Model for Fatigue Life Prediction of Titanium Alloy Welded Joints. Entropy, 21(2), 117. https://doi.org/10.3390/e21020117




