Complex Dynamics in a Memcapacitor-Based Circuit
Abstract
:1. Introduction
2. The Memcapacitor Model and Its Emulator
3. Memcapacitor-Based Chaotic Oscillator and Its Dynamics
3.1. Memcapacitor-Based Chaotic Oscillator
3.2. Equilibrium Points
3.3. Parameters Region
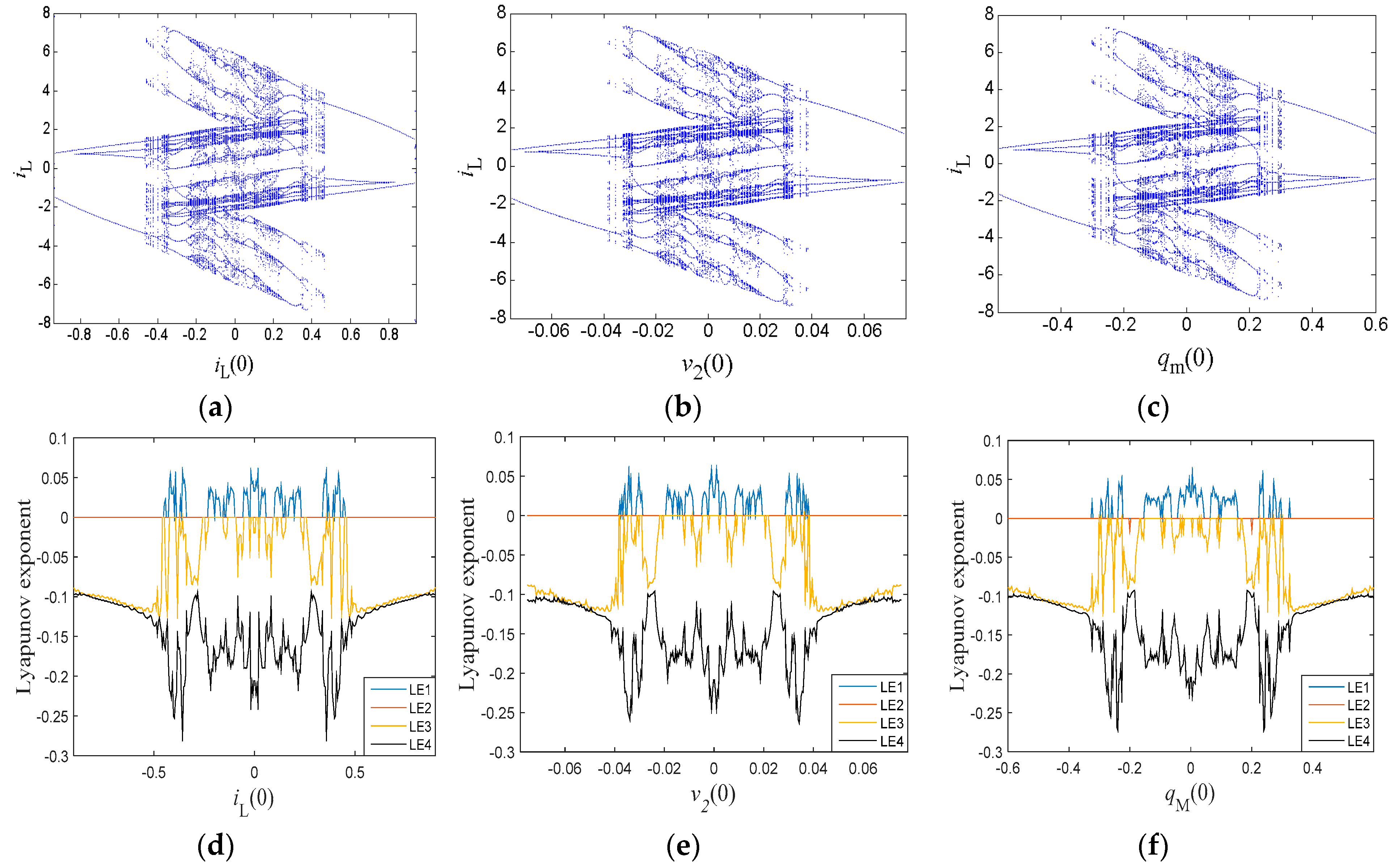
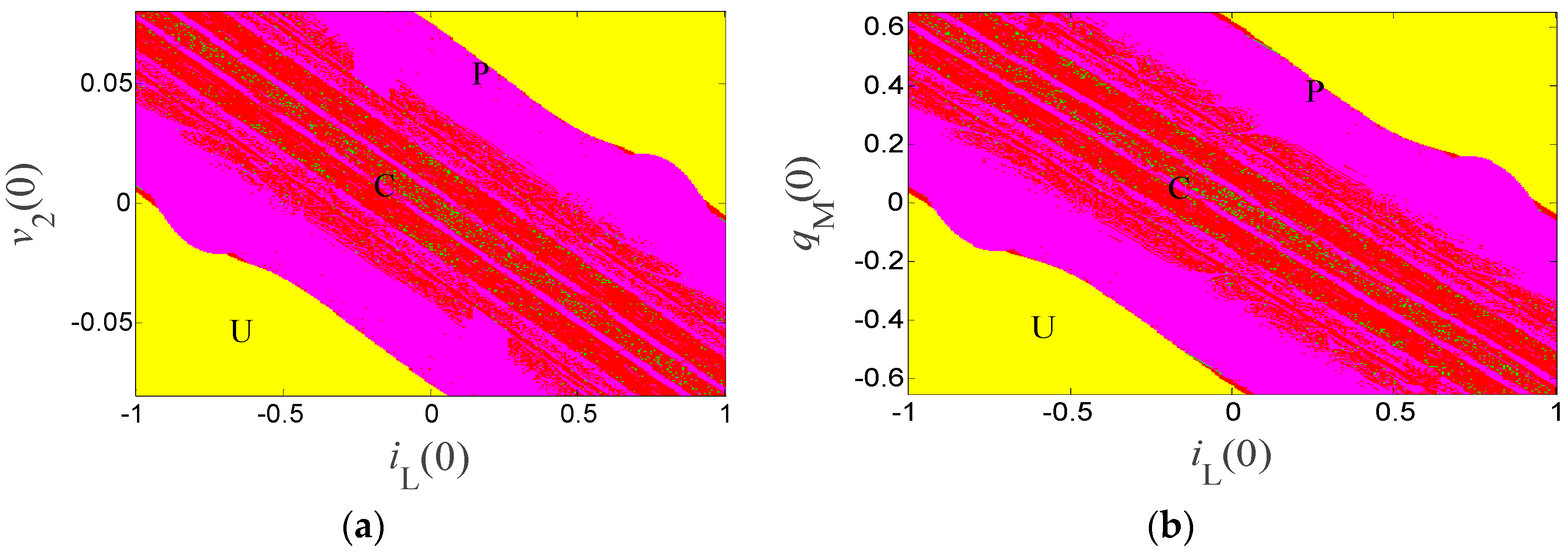
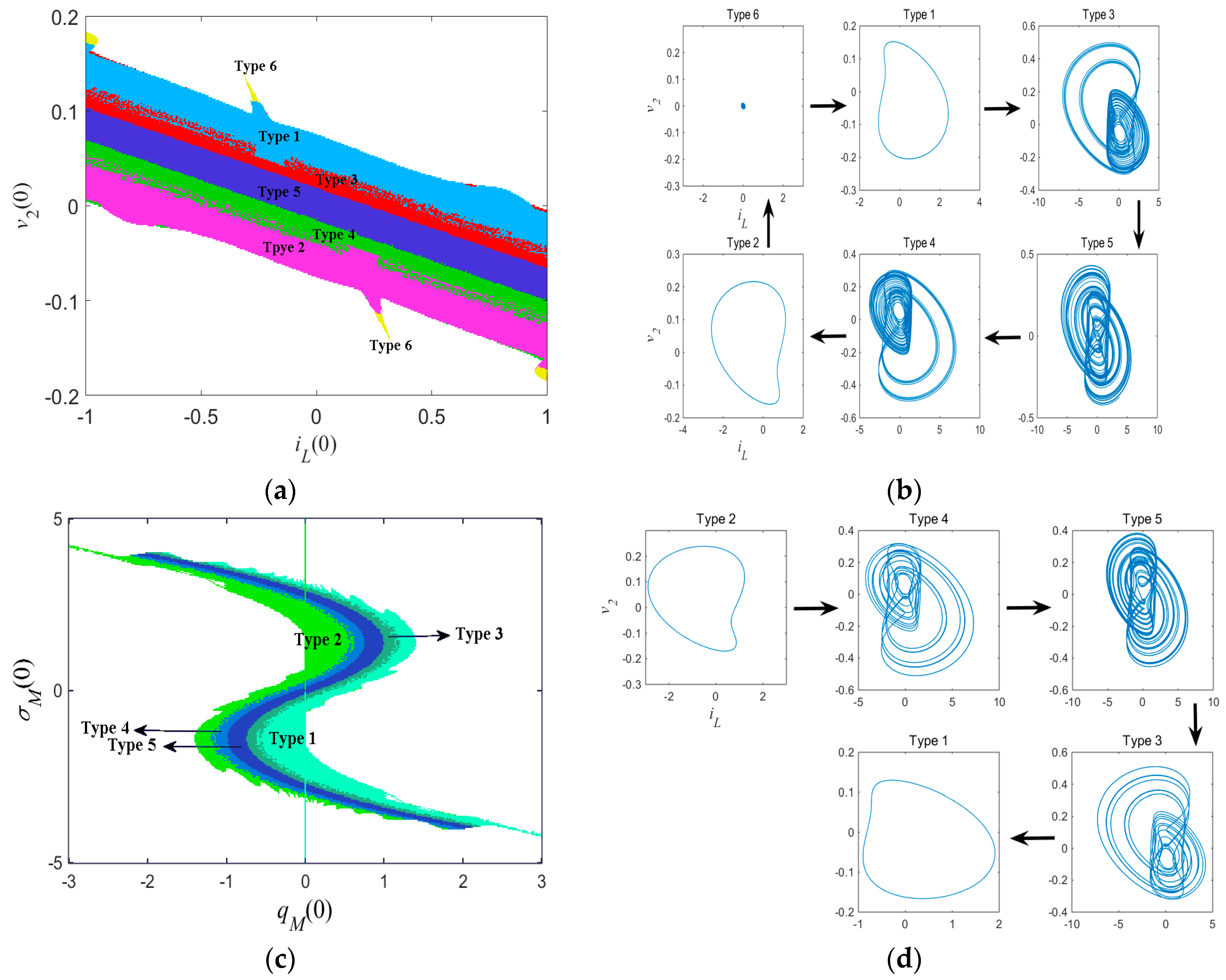
3.4. Similar Bifurcation Structures with Initial Conditions
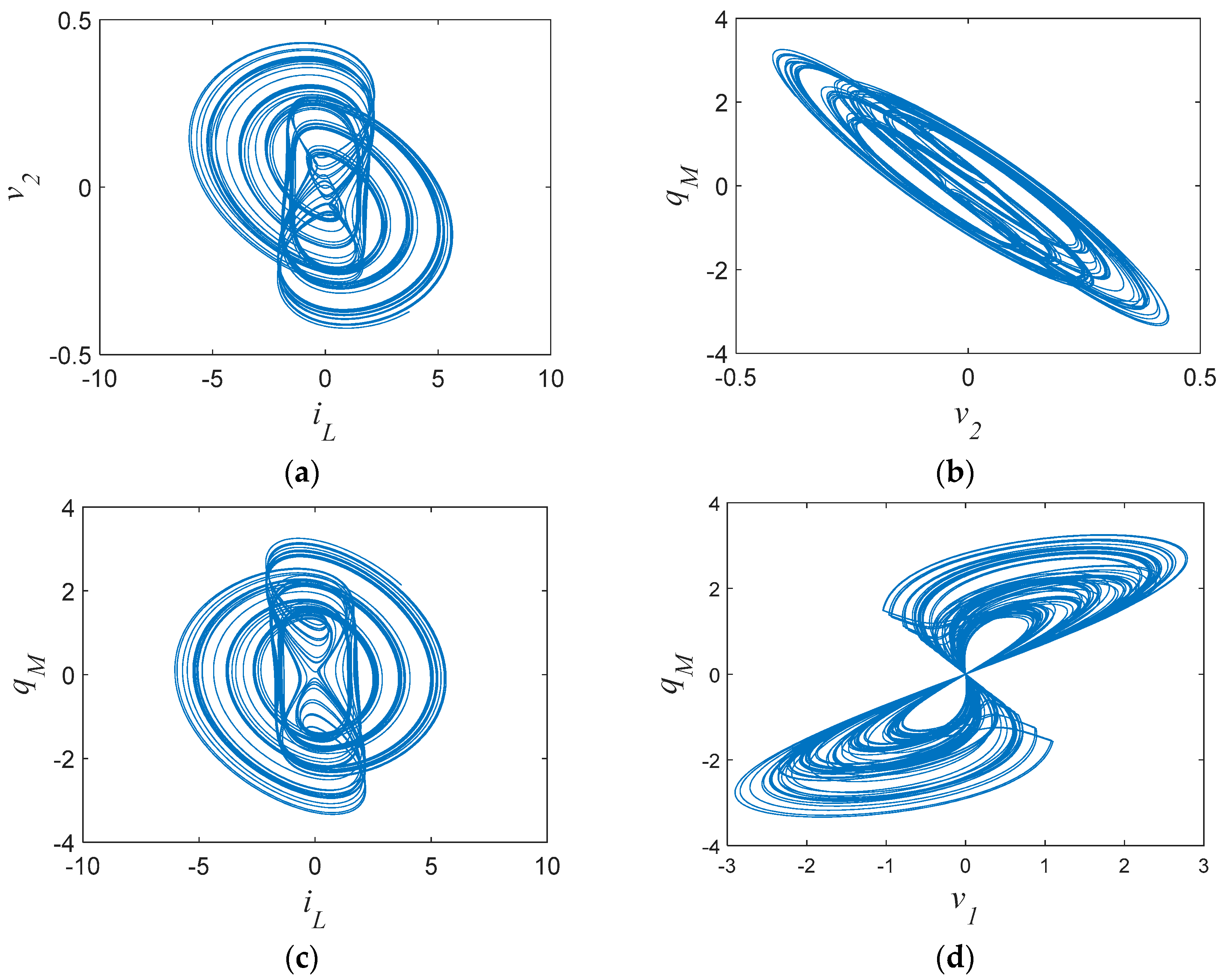
3.5. Extreme Multistability and Coexisting Attractors
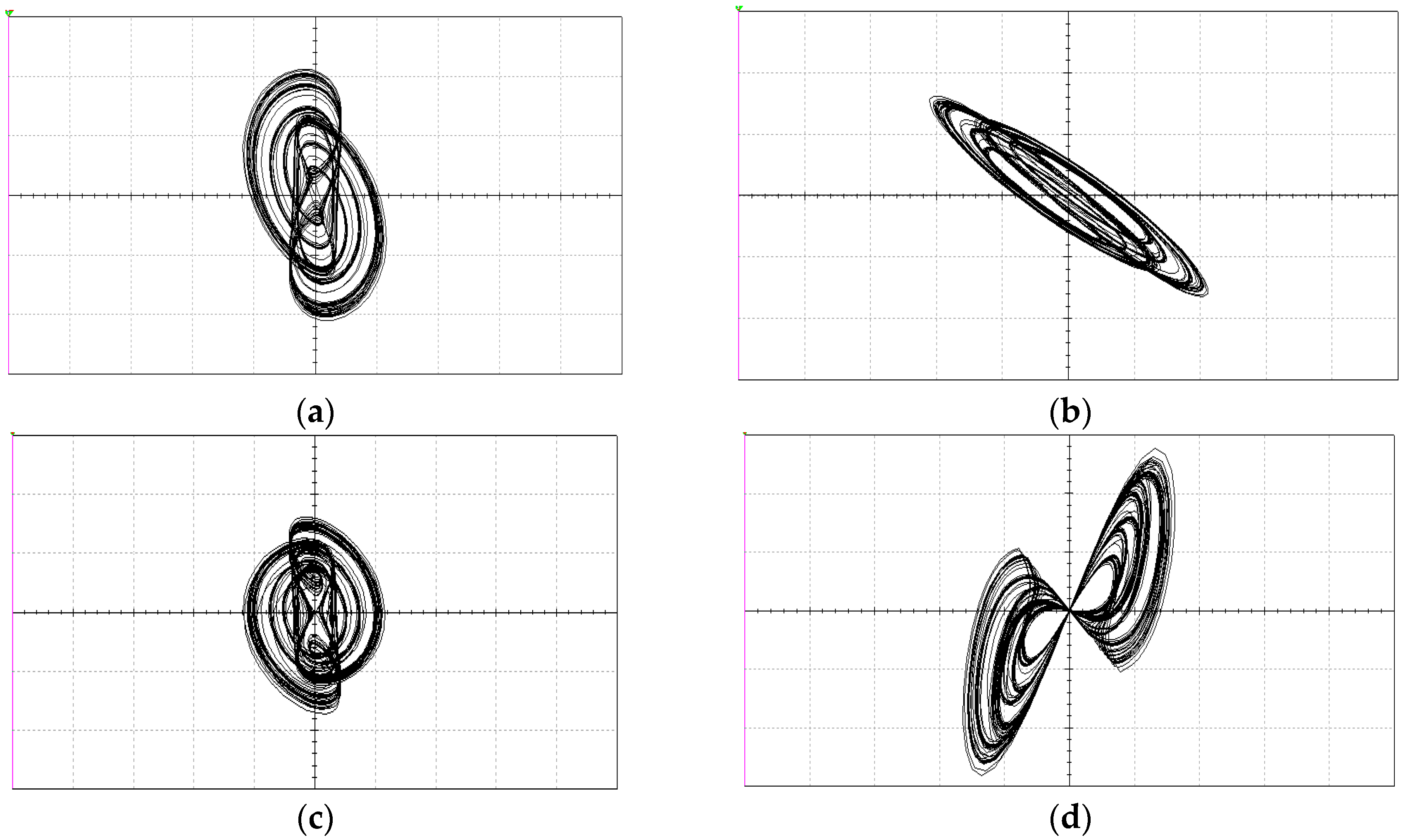
4. Experimental Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Ventra, M.D.; Pershin, Y.V.; Chua, L.O. Circuit elements with memory: Memristors, memcapacitors and meminductors. Proc. IEEE 2009, 97, 1717–1724. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Rincon, J.; Pershin, Y.V. Bistable non-volatile elastic membrane memcapacitor exhibiting chaotic behavior. IEEE Trans. Electron Dev. 2011, 58, 1809–1812. [Google Scholar] [CrossRef]
- Lai, Q.; Zhang, L.; Li, Z.; Stickle, W.F.; Williams, R.S.; Chen, Y. Analog memory capacitor based on field-configurable ion-doped polymers. Appl. Phys. Lett. 2009, 95, 213503. [Google Scholar] [CrossRef]
- Guo, M.; Xue, Y.B.; Gao, Z.H.; Zhang, Y.M.; Dou, G.; Li, Y.X. Dynamic analysis of a physical SBT memristor-based chaotic circuit. Int. J. Bifurc. Chaos 2017, 27, 1730047. [Google Scholar] [CrossRef]
- Wang, S.B.; Wang, X.Y.; Zhou, Y.F. A memristor-based complex lorenz system and its modified projective synchronization. Entropy 2015, 17, 7628–7644. [Google Scholar] [CrossRef]
- Wang, S.B.; Wang, X.Y.; Zhou, Y.F.; Han, B. A memristor-based hyperchaotic complex Lu system and its adaptive complex generalized synchronization. Entropy 2016, 18, 58. [Google Scholar] [CrossRef]
- Xi, H.L.; Li, Y.X.; Huang, X. Generation and nonlinear dynamical analyses of fractional-order memristor-based Lorenz systems. Entropy 2014, 16, 6240–6253. [Google Scholar] [CrossRef]
- Chen, M.; Yu, J.J.; Yu, Q.; Li, C.D.; Bao, B.C. A memristive diode bridge-based canonical chua’s circuit. Entropy 2014, 16, 6464–6476. [Google Scholar] [CrossRef]
- Martinez-Rincon, J.; Di Ventra, M.; Pershin, Y.V. Solid-state memcapacitive system with negative and diverging capacitance. Phys. Rev. B 2010, 81, 195430. [Google Scholar] [CrossRef]
- Biolek, D.; Biolek, Z.; Biolkova, V. Behavioral modeling of memcapacitor. Radioengineering 2011, 20, 228–233. [Google Scholar]
- Biolek, D.; Biolek, Z.; Biolkova, V. Spice modeling of memcapacitor. Electron. Lett. 2010, 46, 520–521. [Google Scholar] [CrossRef]
- Fouda, M.E.; Radwan, A.G. Memcapacitor response under step and sinusoidal voltage excitations. Microelectron. J. 2014, 45, 1372–1379. [Google Scholar] [CrossRef]
- Biolek, D.; Biolkova, V. Mutator for transforming memristor into memcapacitor. Electron. Lett. 2010, 46, 1428–1429. [Google Scholar] [CrossRef]
- Fouda, M.E.; Radwan, A.G. Boundary dynamics of memcapacitor in voltage-excited circuits and relaxation oscillators. Circuits Syst. Signal Process. 2015, 34, 2765–2783. [Google Scholar] [CrossRef]
- Wang, G.Y.; Shi, C.B.; Wang, X.W.; Yuan, F. Coexisting oscillation and extreme multistability for a memcapacitor-based circuit. Math. Probl. Eng. 2017, 2017, 6504969. [Google Scholar] [CrossRef]
- Yu, D.S.; Zhou, Z.; Iu, H.H.C.; Fernando, T.; Hu, Y.H. A coupled memcapacitor emulator-based relaxation oscillator. IEEE Trans. Circuits Syst. II-Express Briefs 2016, 63, 1101–1105. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, G.Y.; Shen, Y.R.; Wang, X.Y. Coexisting attractors in a memcapacitor-based chaotic oscillator. Nonlinear Dyn. 2016, 86, 37–50. [Google Scholar] [CrossRef]
- Wang, G.Y.; Zang, S.C.; Wang, X.Y.; Yuan, F.; Iu, H.H.C. Memcapacitor model and its application in chaotic oscillator with memristor. Chaos 2017, 27, 013110. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, G.Y.; Wang, X.W. Chaotic oscillator containing memcapacitor and meminductor and its dimensionality reduction analysis. Chaos 2017, 27, 033103. [Google Scholar] [CrossRef]
- Rajagopal, K.; Akgul, A.; Jafari, S.; Aricioglu, B. A chaotic memcapacitor oscillator with two unstable equilibriums and its fractional form with engineering applications. Nonlinear Dyn. 2018, 91, 957–974. [Google Scholar] [CrossRef]
- Yamaletdinov, R.D.; Ivakhnenko, O.V.; Sedelnikova, O.V.; Shevchenko, S.N.; Pershin, Y.V. Snap-through transition of buckled graphene membranes for memcapacitor applications. Sci. Rep. 2018, 8, 3566. [Google Scholar] [CrossRef] [PubMed]
- Lassoued, A.; Boubaker, O. On new chaotic and hyperchaotic systems: A literature survey. Nonlinear Anal. Model. Control 2017, 21, 770–789. [Google Scholar] [CrossRef]
- Feudel, U. Complex dynamics in multistable systems. Int. J. Bifurc. Chaos 2008, 18, 1607–1626. [Google Scholar] [CrossRef]
- Ngonghala, C.; Feudel, U.; Showalter, K. Extreme multistability in a chemical model system. Phys. Rev. E 2011, 83, 056206. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Sun, M.X.; Bao, B.C.; Wu, H.G.; Xu, Q.; Wang, J. Controlling extreme multistability of memristor emulator-based dynamical circuit in flux-charge domain. Nonlinear Dyn. 2018, 91, 1395–1412. [Google Scholar] [CrossRef]
- Bao, H.; Jiang, T.; Chu, K.B.; Chen, M.; Xu, Q.; Bao, B.C. Memristor-based canonical Chua’s circuit: Extreme multistability in voltage-current domain and its controllability in flux-charge domain. Complexity 2018, 2018, 5935637. [Google Scholar] [CrossRef]
- Boubaker, O.; Jafari, S. Recent Advances in Chaotic Systems and Synchronization: From Theory to Real World Applications, 1st ed.; Elsevier Academic Press: London, UK, 2018. [Google Scholar]
- Rajagopal, K.; Jafari, S.; Karthikeyan, A.; Srinivasan, A.; Ayele, B. Hyperchaotic memcapacitor oscillator with infinite equilibria and coexisting attractors. Circuits Syst. Signal Process. 2018, 37, 3702–3724. [Google Scholar] [CrossRef]











| Parameters | Meanings | Values |
|---|---|---|
| L | Inductance | 0.3 mH |
| C1 | Capacitor | 7.8 nF |
| G1 | Conductance | 0.42 mS |
| G2 | Conductance | 2.2 mS |
| a | Variable | −0.7 |
| b | Variable | 0.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, F.; Li, Y.; Wang, G.; Dou, G.; Chen, G. Complex Dynamics in a Memcapacitor-Based Circuit. Entropy 2019, 21, 188. https://doi.org/10.3390/e21020188
Yuan F, Li Y, Wang G, Dou G, Chen G. Complex Dynamics in a Memcapacitor-Based Circuit. Entropy. 2019; 21(2):188. https://doi.org/10.3390/e21020188
Chicago/Turabian StyleYuan, Fang, Yuxia Li, Guangyi Wang, Gang Dou, and Guanrong Chen. 2019. "Complex Dynamics in a Memcapacitor-Based Circuit" Entropy 21, no. 2: 188. https://doi.org/10.3390/e21020188
APA StyleYuan, F., Li, Y., Wang, G., Dou, G., & Chen, G. (2019). Complex Dynamics in a Memcapacitor-Based Circuit. Entropy, 21(2), 188. https://doi.org/10.3390/e21020188





