A New Technique Based on Voronoi Tessellation to Assess the Space-Dependence of Categorical Variables
Abstract
:1. Introduction
2. Formal Problem Statement
3. Assessing the Relationship between and Y
3.1. Transforming Y into a Real Variable Z. Spatial Autocorrelation
Spatial Autocorrelation
3.2. Quantizing . Mutual Information Based Index
3.3. Herrera’s Index
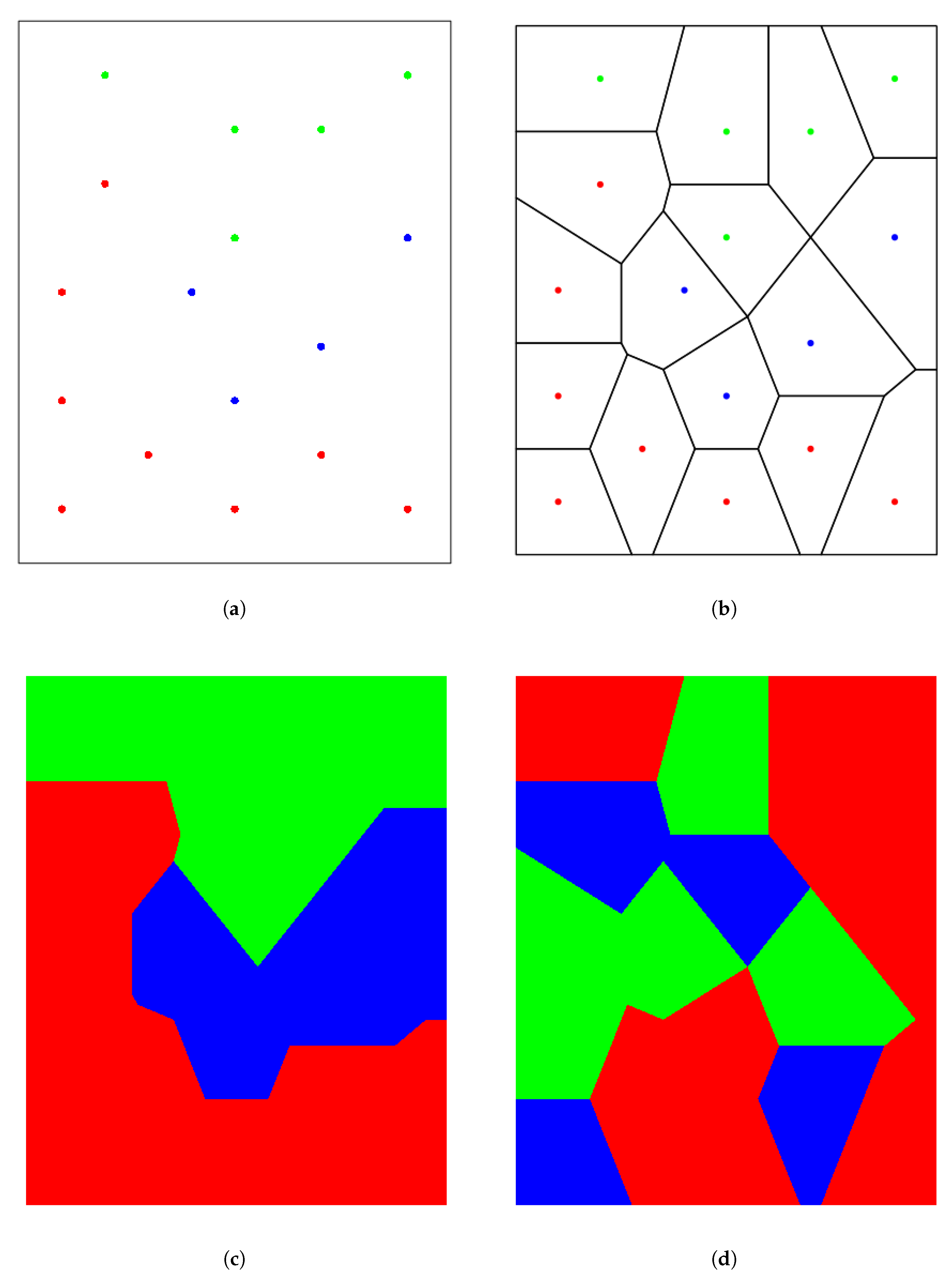
3.4. Voronoi Tessellation Based Index
4. Comparative Evaluation of Indexes
4.1. Simulation Examples
4.1.1. Detailed Analysis for
4.1.2. Influence of the Value of Parameter a
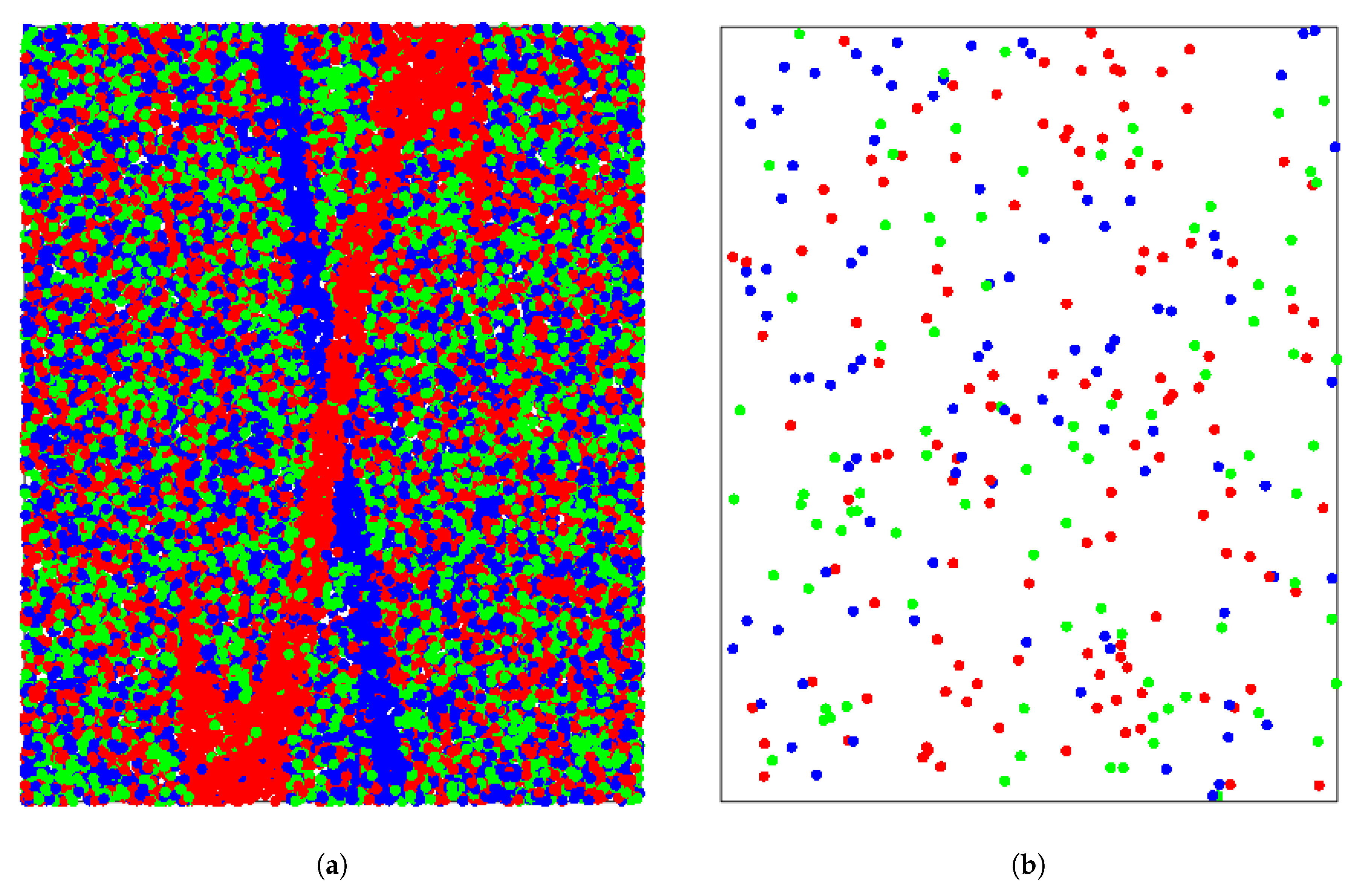
4.2. Telephone Social Network Community Distribution in Cities
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CDRs | Call Detail Records |
| ANOVA | Analysis of variance |
| MANOVA | Multivariate Analysis of Variance |
References
- Diggle, P.J. Statistical Analysis of Spatial Point Patterns; Academic Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Cressie, N. Statistics for spatial data. Terra Nova 1992, 4, 613–617. [Google Scholar] [CrossRef]
- Davis, J.C.; Sampson, R.J. Statistics and Data Analysis in Geology; Wiley: New York, NY, USA, 1986; Volume 646. [Google Scholar]
- White, M.J. The measurement of spatial segregation. Am. J. Sociol. 1983, 88, 1008–1018. [Google Scholar] [CrossRef]
- Morisita, M. Measuring of the dispersion of individuals and analysis of the distributional patterns. Mem. Fac. Sci. Kyushu Univ. Ser. E 1959, 2, 5–23. [Google Scholar]
- Clark, P.J.; Evans, F.C. Distance to nearest neighbor as a measure of spatial relationships in populations. Ecology 1954, 35, 445–453. [Google Scholar] [CrossRef]
- Moran, P.A. The interpretation of statistical maps. J. R. Stat. Soc. Ser. B 1948, 10, 243–251. [Google Scholar] [CrossRef]
- Geary, R.C. The contiguity ratio and statistical mapping. Inc. Stat. 1954, 5, 115–146. [Google Scholar] [CrossRef]
- Ripley, B.D. The second-order analysis of stationary point processes. J. Appl. Probab. 1976, 13, 255–266. [Google Scholar] [CrossRef] [Green Version]
- Candia, J.; González, M.C.; Wang, P.; Schoenharl, T.; Madey, G.; Barabási, A.L. Uncovering individual and collective human dynamics from mobile phone records. J. Phys. A Math. Theor. 2008, 41, 224015. [Google Scholar] [CrossRef]
- Zufiria, P.J.; Pastor-Escuredo, D.; Úbeda-Medina, L.; Hernandez-Medina, M.A.; Barriales-Valbuena, I.; Morales, A.J.; Jacques, D.C.; Nkwambi, W.; Diop, M.B.; Quinn, J.; et al. Identifying seasonal mobility profiles from anonymized and aggregated mobile phone data. Application in food security. PLoS ONE 2018, 13, e0195714. [Google Scholar] [CrossRef] [PubMed]
- Beraldi, P.; Bruni, M.E. A probabilistic model applied to emergency service vehicle location. Eur. J. Oper. Res. 2009, 196, 323–331. [Google Scholar] [CrossRef]
- Alvaro-Hermana, R.; Fraile-Ardanuy, J.; Zufiria, P.J.; Knapen, L.; Janssens, D. Peer to peer energy trading with electric vehicles. IEEE Intell. Transp. Syst. Mag. 2016, 8, 33–44. [Google Scholar] [CrossRef]
- Bin, S.; Yuan, L.; Xiaoyi, W. Research on data mining models for the internet of things. In Proceedings of the Image Analysis and Signal Processing (IASP), Zhejiang, China, 9–11 April 2010; pp. 127–132. [Google Scholar]
- Luong, N.C.; Hoang, D.T.; Wang, P.; Niyato, D.; Kim, D.I.; Han, Z. Data collection and wireless communication in Internet of Things (IoT) using economic analysis and pricing models: A survey. IEEE Commun. Surv. Tutor. 2016, 18, 2546–2590. [Google Scholar] [CrossRef]
- Chen, C.P.; Zhang, C.Y. Data-intensive applications, challenges, techniques and technologies: A survey on Big Data. Inf. Sci. 2014, 275, 314–347. [Google Scholar] [CrossRef]
- Blondel, V.D.; Guillaume, J.L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef] [Green Version]
- Herrera, C. Socio Geographical Patterns Inferred From Mobile Phone Records. Ph.D. Thesis, Universidad Politécnica de Madrid, Madrid, Spain, 2017. [Google Scholar]
- McDonald, J.H. Handbook of Biological Statistics; Sparky House Publishing: Baltimore, MD, USA, 2009; Volume 2. [Google Scholar]
- Pearson, K.X. On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1900, 50, 157–175. [Google Scholar] [CrossRef]
- Gretton, A.; GyĂśrfi, L. Consistent nonparametric tests of independence. J. Mach. Learn. Res. 2010, 11, 1391–1423. [Google Scholar]
- Kraskov, A.; Stögbauer, H.; Grassberger, P. Estimating mutual information. Phys. Rev. E 2004, 69, 066138. [Google Scholar] [CrossRef] [PubMed]
- Pál, D.; Póczos, B.; Szepesvári, C. Estimation of Rényi entropy and mutual information based on generalized nearest-neighbor graphs. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 6–9 December 2010; pp. 1849–1857. [Google Scholar]
- Sricharan, K.; Raich, R.; Hero, A.O. Estimation of nonlinear functionals of densities with confidence. IEEE Trans. Inf. Theory 2012, 58, 4135–4159. [Google Scholar] [CrossRef]
- Sricharan, K.; Raich, R.; Hero III, A.O. Empirical estimation of entropy functionals with confidence. arXiv 2010, arXiv:1012.4188. [Google Scholar]
- Gretton, A.; Bousquet, O.; Smola, A.; Schölkopf, B. Measuring statistical dependence with Hilbert-Schmidt norms. In Proceedings of the International Conference on Algorithmic Learning Theory, Singapore, 8–11 October 2005; pp. 63–77. [Google Scholar]
- Sejdinovic, D.; Sriperumbudur, B.; Gretton, A.; Fukumizu, K. Equivalence of distance-based and RKHS-based statistics in hypothesis testing. Ann. Stat. 2013, 41, 2263–2291. [Google Scholar] [CrossRef]
- Székely, G.J.; Rizzo, M.L.; Bakirov, N.K. Measuring and testing dependence by correlation of distances. Ann. Stat. 2007, 35, 2769–2794. [Google Scholar] [CrossRef]
- García, J.E.; González-López, V.A. Independence tests for continuous random variables based on the longest increasing subsequence. J. Multivar. Anal. 2014, 127, 126–146. [Google Scholar] [CrossRef]
- Ross, B.C. Mutual information between discrete and continuous data sets. PLoS ONE 2014, 9, e87357. [Google Scholar] [CrossRef] [PubMed]
- Zufiria, P.J.; Hernandez-Medina, M.A. Characterizing the Spatial Distribution of Geolocated Categorical Values. Int. J. Appl. Phys. Math. 2019, 9, 47–53. [Google Scholar] [CrossRef]
- Garson, G.D. Testing Statistical Assumptions; Statistical Associates Publishing: Asheboro, NC, USA, 2012. [Google Scholar]
- Light, R.J.; Margolin, B.H. An analysis of variance for categorical data. J. Am. Stat. Assoc. 1971, 66, 534–544. [Google Scholar] [CrossRef]
- Leibovici, D.G.; Bastin, L.; Jackson, M. Higher-order co-occurrences for exploratory point pattern analysis and decision tree clustering on spatial data. Comput. Geosci. 2011, 37, 382–389. [Google Scholar] [CrossRef]
- Cliff, A.D.; Ord, K. Spatial autocorrelation: A review of existing and new measures with applications. Econ. Geogr. 1970, 46, 269–292. [Google Scholar] [CrossRef]
- Burridge, P. On the Cliff-Ord test for spatial correlation. J. R. Stat. Soc. Ser. 1980, 42, 107–108. [Google Scholar] [CrossRef]
- Claramunt, C. A spatial form of diversity. In Proceedings of the International Conference on Spatial Information Theory, Ellicottville, NY, USA, 14–18 September 2005; pp. 218–231. [Google Scholar]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S.N. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams; John Wiley & Sons: New York, NY, USA, 2009; Volume 501. [Google Scholar]



| Min | 1st Q. | Median | 3rd Q. | Max | Mean | Std | |
|---|---|---|---|---|---|---|---|
| Moran I () | 0 | 0.03 | 0.135 | 0.37 | 0.98 | 0.237 | 0.262242 |
| Moran I () | 0 | 0.01 | 0.07 | 0.23 | 0.99 | 0.18735 | 0.261614 |
| Geary C () | 0 | 0.02 | 0.13 | 0.3925 | 0.97 | 0.2405 | 0.267861 |
| Geary C () | 0 | 0.03 | 0.15 | 0.43 | 0.99 | 0.2764 | 0.292252 |
| Mut. Inf. M | 0 | 0.02 | 0.135 | 0.305 | 0.975 | 0.207925 | 0.237545 |
| Herrera D | 0 | 0.05375 | 0.1835 | 0.3825 | 0.935 | 0.239050 | 0.224115 |
| Voronoi E | 0 | 0.0150 | 0.06 | 0.18 | 0.815 | 0.128475 | 0.172679 |
| Paris | Lisbon | Madrid | |
|---|---|---|---|
| Moran I | 0.34 | 0.002 | |
| Geary C | 0.37 | 0.0016 | |
| Mut. Inf. M | 0.0007 | 0.046 | |
| Herrera D | 0.0036 | ||
| Voronoi E | 0.0045 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zufiria, P.J.; Hernández-Medina, M.Á. A New Technique Based on Voronoi Tessellation to Assess the Space-Dependence of Categorical Variables. Entropy 2019, 21, 774. https://doi.org/10.3390/e21080774
Zufiria PJ, Hernández-Medina MÁ. A New Technique Based on Voronoi Tessellation to Assess the Space-Dependence of Categorical Variables. Entropy. 2019; 21(8):774. https://doi.org/10.3390/e21080774
Chicago/Turabian StyleZufiria, Pedro J., and Miguel Á. Hernández-Medina. 2019. "A New Technique Based on Voronoi Tessellation to Assess the Space-Dependence of Categorical Variables" Entropy 21, no. 8: 774. https://doi.org/10.3390/e21080774
APA StyleZufiria, P. J., & Hernández-Medina, M. Á. (2019). A New Technique Based on Voronoi Tessellation to Assess the Space-Dependence of Categorical Variables. Entropy, 21(8), 774. https://doi.org/10.3390/e21080774





