1. Introduction
Space stations have become an indispensable experimental platform for human beings to operate long-term advanced scientific experiments upon in the frontier of space, which has a microgravity environment. The International Space Station (ISS) is humanity’s largest foothold in space [
1]. From 2000, when the first astronauts boarded the ISS, to now, more than 2600 unique experiments have been conducted on the ISS during the past 18 years of continuous research [
2]. The diversity of research means a diversity in the experiments’ environment control requirements and the difficulty of integration. At present, developing standard interface racks (SIRs) [
3] is the best solution.
Standard interface racks are designed around the concept of providing a set of common interfaces for modular experiments [
4]. Expedite the Processing of Experiments to Space Station (EXPRESS) racks are the most widely used SIR, and provide accommodation and facilitates operations for microgravity-based research payloads on the ISS [
5]. There have been many space experiments conducted in EXPRESS racks and similar racks, such as the European Drawer Rack (EDR), which aids with biological experiments, human physiology and adaptation experiments, and physical science experiments [
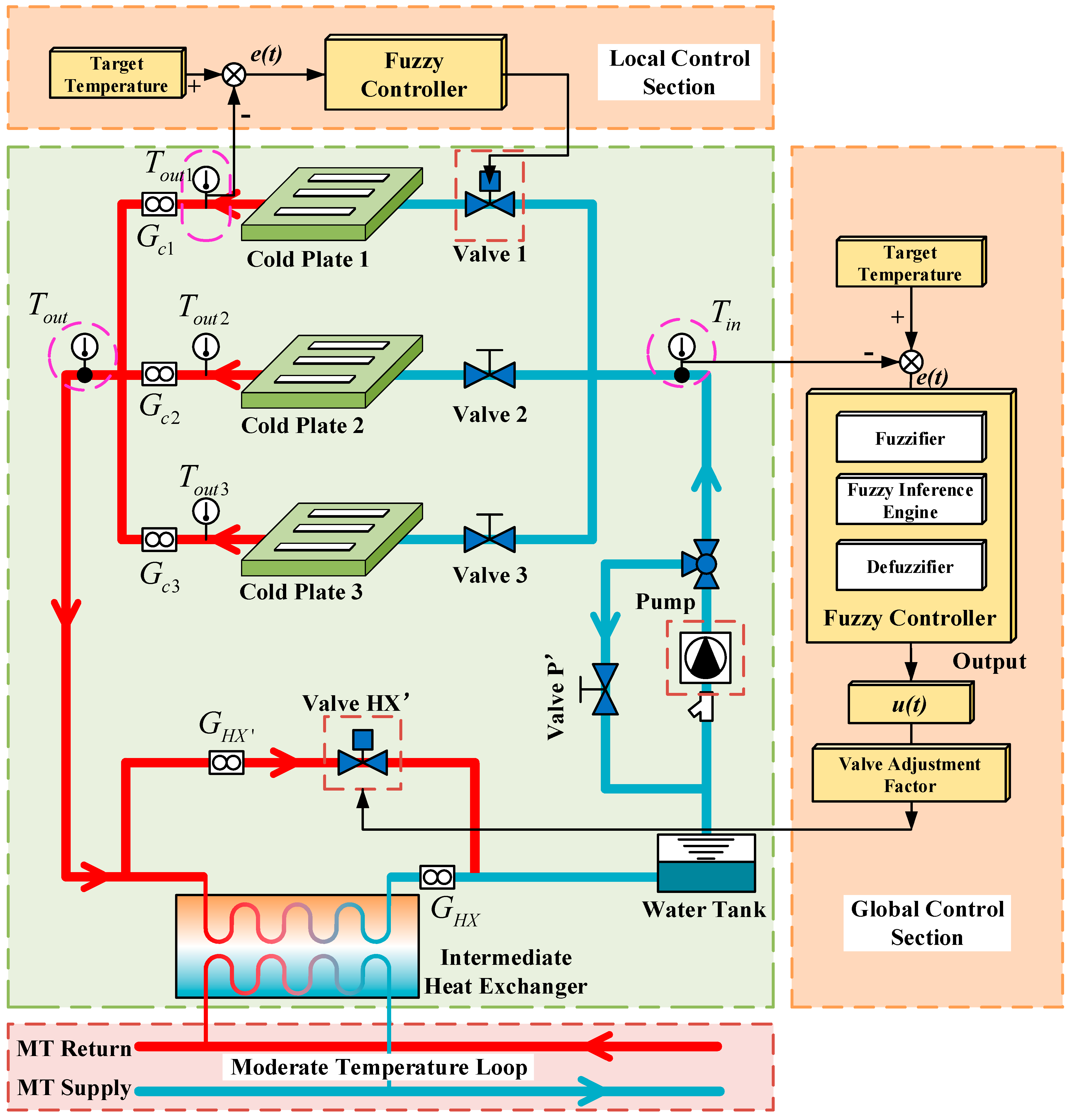
1]. The EXPRESS rack can accommodate eight single middeck lockers and two international subrack interface standard drawers, and in order to realize the thermal control of payloads, a defined Active Thermal Control System (ATCS) Kit has been developed. The ATCS consists of a set of cold plates, some with a heat exchanger, and it provides a mechanism for transporting the heat load generated by the experiments to Internal Thermal Control System (ITCS) loops [
6]. The payloads are in parallel or series connection in the thermal control fluid loop system. Each payload rack is connected to the ITCS, which can supply cooling fluid at 15.6 to 18.3 °C [
7] via a permanently installed kit by flex hose assemblies [
6], and the racks are in parallel connection with each other. Generally, the coolant flow of the ITCS loops flows into the payloads in the rack directly, and the flowrate is regulated by a Rack Flow Control Assembly (RFCA), which includes a modulating valve, a flow sensor, and a temperature sensor. The RFCA is located on the outlet line of the payload rack to maintain either a specific flow rate or a specific outlet temperature as determined by the user [
7], which can realize the thermal control of the rack overall. Owing to the fact that the RFCA cannot control the flowrate of the cold plate branches, the temperature control of experimental payloads requires other accessories, including thermoelectric coolers (TECs), heaters, and fans, etc. In a few applications a heat exchanger is mounted within the experiment facility rack. Each side of the heat exchanger accommodates only one single loop flow, with the ITCS side being designated the cold side and the experiment rack the hot side [
6,
8].
Research on the control strategy of thermal control systems in space stations has focused on ITCS loops, which consist of system flow control assemblies, three-way mixing valves (TWMV), rack flow control assemblies (RFCA), cold plates, pressure sensors, temperature sensors, pump bypass assemblies (PBA), and heat exchangers [
9]. The control algorithm used in thermal control systems in space stations is mainly a traditional PID control algorithm [
10,
11,
12,
13,
14]. In the Columbus module there are two pairs of mixing valves in the water loop cooling system which are controlled by PID regulators to hold temperature set points. Paper [
15] has verified the stability of a control system based on control theory using the thermal software tool ESATAN/FHTS. Valenzano et al. have taken the gain of a control algorithm as a parameter to verify the stability of the control system of Node 2 and 3, with the dangerous conditions of space stations being predicted [
16]. De Palo S et al. have analyzed the stability of the thermal and hydraulic control loop of the Columbus in the ISS by using the theory of automatic control. The stability of the PID algorithm and the system stability when the control parameters change were verified by comparison with ground experiment, simulation, and flight data [
17]. The thermal control system in the Human Research Facility (HRF) experiment rack, which was developed by NASA, has three internal flowrate controllers that use a modulated solenoid valve, flow meter, and a dedicated PID controller [
4].
Compared with the traditional thermal control fluid loop system described above, there are many novel thermal control designs that can be learned despite some of them not being targeted for space stations. Wei Guo et al. have proposed an adaptive thermal control cold plate module (TCCM) which can be used in scientific experimental racks. The TCCM could provide flow rate and temperature co-adjustments by using a Shape-Memory-Alloy (SMA) assembly, which possesses self-driven abilities [
18]. S.H. Lee et al. have proposed a Hybrid Thermal Control System (H-TCS) in which different operational modes are considered, namely, single phase, two-phase, basic heat pump and heat pump with liquid-side, and suction-side heat exchanger. This thermal control system would satisfy the diverse thermal requirements of different space missions [
19]. A novel hardware component called the Sublimator Driven Coldplate (SDC) has been developed under NASA’s Constellation Program. It targets equipment which has a low heat load, short transport distance, and short mission duration requirements, and which has the potential to replace an entire thermal control system with one hardware component [
20]. Kim et al. have suggested a new spacecraft thermal control hardware system composed of two parallel channels working for a heat pipe (HP) and a solid–liquid phase change material (PCM) for a high heat dissipating component which works intermittently with short duty [
21]. As can be seen, related thermal control designs focus on the application of new materials and two-phase systems, which need a great deal of verification for use the spacecraft.
Intelligent control has not been widely used in thermal control systems in space stations and relative studies are scarce. Expert control is simply used to coordinate multiple thermal control subsystems and manage the whole system under some special conditions in the ISS. However, there are studies which have addressed the thermal control of spacecraft, electronic equipment, and so on. Yingnan Cui et al. have proposed an adaptive fuzzy controller for thermal management of microprocessors and have conducted an experiment which demonstrates that the adaptive fuzzy controller maintains control quality when faced with severe variations of the thermal model [
22]. Trevor Hocksun Kwan et al. have proposed a fuzzy logic controller (FLC) which aims at temperature control of fuel cell stacks. Their FLC integrates both a combined Thermoelectric Generator-Thermoelectric Cooler (TEG-TEC) control method and variable coolant rate techniques to achieve both active temperature control (in TEC mode) and energy harvesting capability (in TEG mode) of the thermoelectric device [
23]. Yun-Ze Li et al. have presented a fuzzy coordination control strategy used in a microchannel-heat-exchanger (MHE) space cooling network for future spacecraft, and demonstrated that it has better performance than single-input PID controllers [
24].
In order to achieve more efficient and stable thermal control of scientific experimental racks in space stations, an indirect coupling thermal control fluid loop system is proposed here which has an isolated fluid loop in the rack. Compared with the fluid loop system which connects the cooling fluid of the ITCS directly by flex hose assemblies, it adds an intermediate heat exchanger, a pump assembly, and a number of regulating valves. There are several advantages to the proposed system: (1) it allows the thermal control system in the rack to be designed without having to meet all requirements of the ITCS loops, which have many limitations; (2) any contamination originating in the experiment components or leakage from the secondary cooling loop will be confined at rack level and will not affect other racks; and (3) the temperature of the experimental payloads in the rack can be controlled precisely. A dynamic model of the thermal control system is also built using the software tool AMESim. Then, three intelligent control strategies for the thermal control system which employ two fuzzy incremental controllers are presented, and the difference among these is the input and output of the controller. Finally, a simulation of the three control strategies is performed. In addition, the results of the simulation are compared and analyzed in detail.
3. Results and Discussion
In order to verify the effectiveness of the fuzzy incremental controller and reflect on its advantages, the fuzzy incremental controller is first compared with the PID. The two controllers are, respectively, employed in case 1, in which the controlled variable is the outlet temperature of the cold plate branch
and the control variable is the pump speed
. The other simulation parameters are shown in
Table 6.
The controlled variables of the local controller and global controller, as well as the outlet temperature of the cold plate 1
and the outlet temperature of the cold branch
, are illustrated in
Figure 7. The overshoots and settling times of
and
with the two controllers are shown in
Table 8. As can be seen, the overshoots of the outlet temperature of cold plate 1
are almost the same as for the two controllers, but its settling times in the two stages with the fuzzy incremental controller are shorter than with the PID controller. As for the outlet temperature of the cold branch
, the overshoots in stage one are, respectively, 1.7 °C and 2.4 °C with the fuzzy incremental controller and the PID controller, and, in stage two, 0.8 °C and 1.1 °C. The settling times of the outlet temperature of the cold branch
in the two stages with the fuzzy incremental controller are shorter than those with the PID controller, too. Taken together, the overshoots are smaller and the settling times are shorter for the controlled variables with the fuzzy incremental controller. In other words, the control effect of the fuzzy incremental controller is better than the PID controller in the thermal control system.
3.1. Case 1: The Controlled Variable Is and the Control Variable Is Pump Speed
In case 1, the bypass valve opening of the intermediate heat exchanger is constant. The controlled variable is the outlet temperature of the cold plate branch , the setting temperature is 28 °C, and the control variable is the pump speed .
The inlet and the outlet temperature of the cold branch and the outlet temperature of the cold plates are the main concerns, and are shown in
Figure 8a. To be clear, owing to the fact that cold plate 2 and cold plate 3 are subjected to the same working conditions, only the relevant temperatures of cold plate 2 are shown in the figure. In stage one, all of the temperatures rise rapidly and tend towards stability after about 600 s under the action of the controller. The maximum value of the outlet temperature of the cold plate branch, which is the controlled variable in the global controller, is 30.2 °C, which means that the overshoot is 2.2 °C and the settling time is about 600 s. The maximum value of the outlet temperature of the two cold plates is 30.8 °C and 31.6 °C, respectively. However, it is obvious that the settling time of the outlet temperature of cold plate 1 is shorter, being about 300 s. The inlet temperature of the cold plate branch increases and stabilizes at 22 °C after 600 s. In stage two, the heating power of cold plate 1 jumps from 250 W to 500 W, which causes the outlet temperature of cold plate 1 to rise rapidly; its maximum is 29 °C, which means that the overshoot is 1 °C. The outlet temperature of cold plate 2 and the cold plate branch are increased, and the maxima are, respectively, 28.8 °C and 28.7 °C, which implies that the overshoots are within 1 °C. In addition, there is a slight increase in the inlet temperature of the cold plate branch, which is maintained at about 22 °C after 600 s.
Figure 8b illustrates the variation in cold plate temperature in case 1. In stage one, the highest temperatures of cold plate 1 and cold plate 2 are 40.3 °C and 43.9 °C, respectively. The temperature of cold plate 1 is stable after 350 s, but cold plate 2 reaches a stable temperature range after 500 s. The temperatures of the two cold plates are basically the same, being about 38.5 °C, in the steady state. In stage two, the temperature of cold plate 1 rises rapidly and finally stabilizes at 44.3 °C, while there is a slight rise in the temperature of cold plate 2.
Main causes for the occurrence of the said phenomena can be explained by the variations in pump speed, the valve openings of cold plate branches, and the flowrate, which are shown in
Figure 9. In stage one, the pump speed rapidly increases, which leads to an increase in the total flowrate of the loop. The valve opening of the cold plate 1 branch also rapidly increases, and with the effect of these two aspects, the flowrate of the cold plate 1 branch increases much faster than that of the cold plate 2 branch. As can be seen from
Figure 9c, the flowrate of the cold plate 1 branch reaches a stable range after 200 s, but the cold plate 2 branch takes about 400 s to do so. Accordingly, the responses of cold plate 1’s relevant temperatures are faster than those of cold plate 2. In stage two, the valve opening of the cold plate 1 branch rapidly increases, resulting in a sharp increase in the flowrate of the cold plate 1 branch, which also leads to a decrease in the flowrate of the cold plate 2 branch. As a result, the temperature of cold plate 1 overshoots over a period of time.
3.2. Case 2: The Controlled Variable Is and the Control Variable Is
In case 2, the pump speed is constant and is set as 1000 rev/min. The controlled variable is the outlet temperature of the cold plate branch, the setting temperature is 28 °C, and the control variable is the bypass valve opening of the intermediate heat exchanger.
The inlet and the outlet temperature of the cold plate branch and the outlet temperature of the cold plates are the main concerns of case 2, as is shown in
Figure 10a. In stage one, all the temperatures rise rapidly and tend towards stability after about 2000 s under the action of the controller. The maximum value of the outlet temperature of the cold plate branch, which is the controlled variable in the global controller, is 28.5 °C, which means that the overshoot is tiny and is merely around 0.5 °C. The maximum values of the outlet temperature of the two cold plates are 28.5 °C and 28.7 °C, respectively. However, it is obvious that the settling time of the outlet temperature of cold plate 1 is shorter, being about 200 s. By contrast, cold plate 2, which is without the local controller, takes about 2000 s to get the same state. The inlet temperature of the cold plate branch is maintained at about 22.5 °C after 2000 s. In stage two, the heating power of cold plate 1 jumps from 250 W to 500 W, which causes the outlet temperature of cold plate 1 to rise rapidly; its maximum is 29.7 °C, which means its overshoot is 1.7 °C. The settling time is 1500 s. The outlet temperature of cold plate 2 and the cold plate branch increase and reach stability after 1500 s. Their maxima are, respectively, 30 °C and 29.6 °C. In addition, there is a decrease in the inlet temperature of the cold plate branch, which is maintained at about 20.7 °C after 1500 s.
Figure 10b illustrates the variation in the cold plate temperature in case 2. In stage one, the highest temperatures of cold plate 1 are 39.5 °C and 39 °C, respectively. The temperatures of the two cold plates are basically the same, being about 38.3 °C, in the stable state. In stage two, the temperature of cold plate 1 rises rapidly and is finally stabilized at 45.7 °C, and attains a stable state soon after. The highest temperature of cold plate 1 is 41.4 °C, and the temperature stabilizes at 39.4 °C after 1500 s.
The main causes for the occurrence of the said phenomena in case 2 can be explained by the variations of the bypass valve opening of the intermediate heat exchanger, the valve openings of the cold plate branches, and the flowrate, which are shown in
Figure 11. In stage one, the bypass valve opening of the heat exchanger increases because the outlet temperature of the cold plate branch is temporarily lower than the set temperature, which leads to a decrease in the flowrate through the hot side of the heat exchanger. The valve opening of the cold plate 1 branch increases, which leads to the flowrate of cold plate 1 branch increasing and for the flowrate of cold plate 2 branch to experience a relatively small decrease. That is to say, the change trends of the flowrate of the two plate branches are the opposite of one another. Hence, the outlet temperature of cold plate 1 and its temperature respond faster because the flowrate of the branch is small at the beginning. The flowrates of the two cold plate branches are, respectively, 38.7 kg/h and 39.4 kg/h after reaching a stable state result in the outlet temperature of the two cold plate branches, and the two cold plate temperatures are almost the same. In stage two, the valve opening of the cold plate 1 branch rapidly increases, resulting in a sharp increase in the flowrate of the cold plate 1 branch, which also leads to a decrease in the flowrate of the cold plate 2 branch. As a result, the temperature of the two cold plates are increased. Additionally, the bypass valve opening of the heat exchanger is decreased, rapidly bringing about an increase in the flowrate through the hot side of the heat exchanger, increasing the heat exchange between the SWL and the PWL.
3.3. Case 3: The Controlled Variable Is and the Control Variable Is
In case 3, the parameter settings are the same as in case 2, except for the fact that the controlled variable is the inlet temperature of the cold plate branch and that the setting temperature is 21 °C.
The inlet and the outlet temperature of the cold plate branch and the outlet temperature of the cold plates are the main concerns of case 3, as is shown in
Figure 12a. In stage one, all of the temperatures rise rapidly and tend towards stability after about 1000 s under the action of the controller. The maximum value of the inlet temperature of the cold plate branch, which is the controlled variable in the global controller, is 21.3 °C, which means that the overshoot is tiny, being merely around 0.3 °C. The maximum values of the outlet temperature of the two cold plates are 28.5 °C and 26.9 °C, respectively. However, it is obvious that the settling time of the outlet temperature of cold plate 1 is shorter, being about 300 s. Cold plate 2, which is the local controller, takes 1000 s to get the same state. Additionally, the outlet temperatures of cold plate 1 and cold plate 2 are, respectively, 28 °C and 26.1 °C, and there is a temperature difference of about 2 °C. In addition, there is an increase in the outlet temperature of the cold plate branch which is maintained at about 26.6 °C after about 1000 s. In stage two, the heating power of cold plate 1 jumps from 250 W to 500 W, which causes the outlet temperature of cold plate 1 to rise rapidly, and its maximumt is 29.3 °C. After 1000 s, it is maintained at about 27.9 °C. The outlet temperatures of cold plate 2 and the cold plate branch increase, and are, respectively, 28.4 and 28.2 °C in the stable state.
Figure 12b illustrates the variation in the cold plate temperature in case 3. In stage one, the temperature of cold plate 1 is stable after 200 s, but cold plate 2 reaches a stable temperature range after 750 s. The temperatures of the two cold plates are 39.3 °C and 36.3 °C, respectively, in the steady state. In stage two, the temperature of cold plate 1 rises rapidly and finally stabilizes at 45.5 °C, while the temperature of cold plate 2 finally stabilizes at 40 °C.
The variations in the bypass valve opening of the intermediate heat exchanger, the valve openings of the cold plate branches, and the flowrate in case 3 are shown in
Figure 13a. In stage one, the trend of the bypass valve opening of the heat exchanger and the valve opening of the cold plate 1 branch is as same as in case 1, but it is more responsive in case 3. The flowrates of the two cold plate branches are, respectively, 30 kg/h and 41 kg/h; after reaching the stable state this results in the outlet temperature of the cold plate 1 branch and the cold plate 1 temperature being higher than cold plate 2. In stage two, the trends are also the same as in case 2, except for the different response speed and the values of the valve opening in the stable state. A comparison is given in the following section.
3.4. Comparison of the Three Cases
The control strategy at the local level for cold plate 1 in the three cases shows no difference; the control variable is the valve opening of cold plate 1 and the controlled variable is the outlet temperature of the cold plate. The difference is seen within the control strategy at the global level, and, therefore, the focal point of the comparison is the impact of the global control strategy on the system.
The outlet temperature of cold plate 1 is shown in
Figure 14a. In stage one, the overshoot of case 1 is the biggest, while it kept within 1 °C in case 2 and case 3, and is 30.8 °C. However, the temperature is controlled within 1 °C in about 100 s and reaches the stable state in 400 s in case 1. In stage two, case 1 has the smallest overshoot and the shortest time to obtain a stable state, but with case 2 it is the opposite.
Figure 14b illustrates the variation in cold plate 1’s temperature in the three cases. In stage one, the temperature of cold plate 1 is both 38.5 ± 0.8 °C in the three cases, and in stage two it is both 45.5 ± 0.8 °C, which is the smallest difference observed. In all cases, the temperature of cold plate 1 does not exceed 50 °C, which meets the requirements. However, when comparing the stable temperature of the two stages, the temperature differences of the two stages in the three cases are 5.5 °C, 7.4 °C, and 6.3 °C, respectively. In terms of stable time, case 2 takes the longest.
Figure 14c illustrates the variation in cold plate 2’s temperature in the three cases. In stage one, the maximum value of the temperature is 43.8 °C at first in case 1, and the temperature reaches a stable state after 600 s. In the stable state, the temperatures are about 38 °C in both case 1 and case 2, while in case 3 the temperature 36.3 °C, which is the smallest stable temperature. In stage one, the temperatures are similar to one another, being 39 ± 0.8 °C. As for the temperature differences of the two stages in the stable state, in the three cases these are 0.2 °C, 1.3 °C, and 3.3 °C, respectively. It is obvious that the change in cold plate 2’s temperature is the biggest in case 3.
Taken together, without considering pump loss, case 1, in which the controlled variable is and the control variable is the pump speed, is the best choice. However, there are still situations in which the pump is not adjustable to reduced wear, and to prolong the service life of it, case 2, in which the controlled variable is and the control variable is , can be used. However, there is no denying that the response of the control strategy is slower than in case 1. Case 3, in which the controlled variable is and the control variable is , may not be considered because the regulation of the cold plate 1 branch has a big impact on the stability of cold plate 2’s temperature, although the heating power of cold plate 2 is constant all the time.