Exergy Analysis of Advanced Adsorption Cooling Cycles
Abstract
:1. Introduction
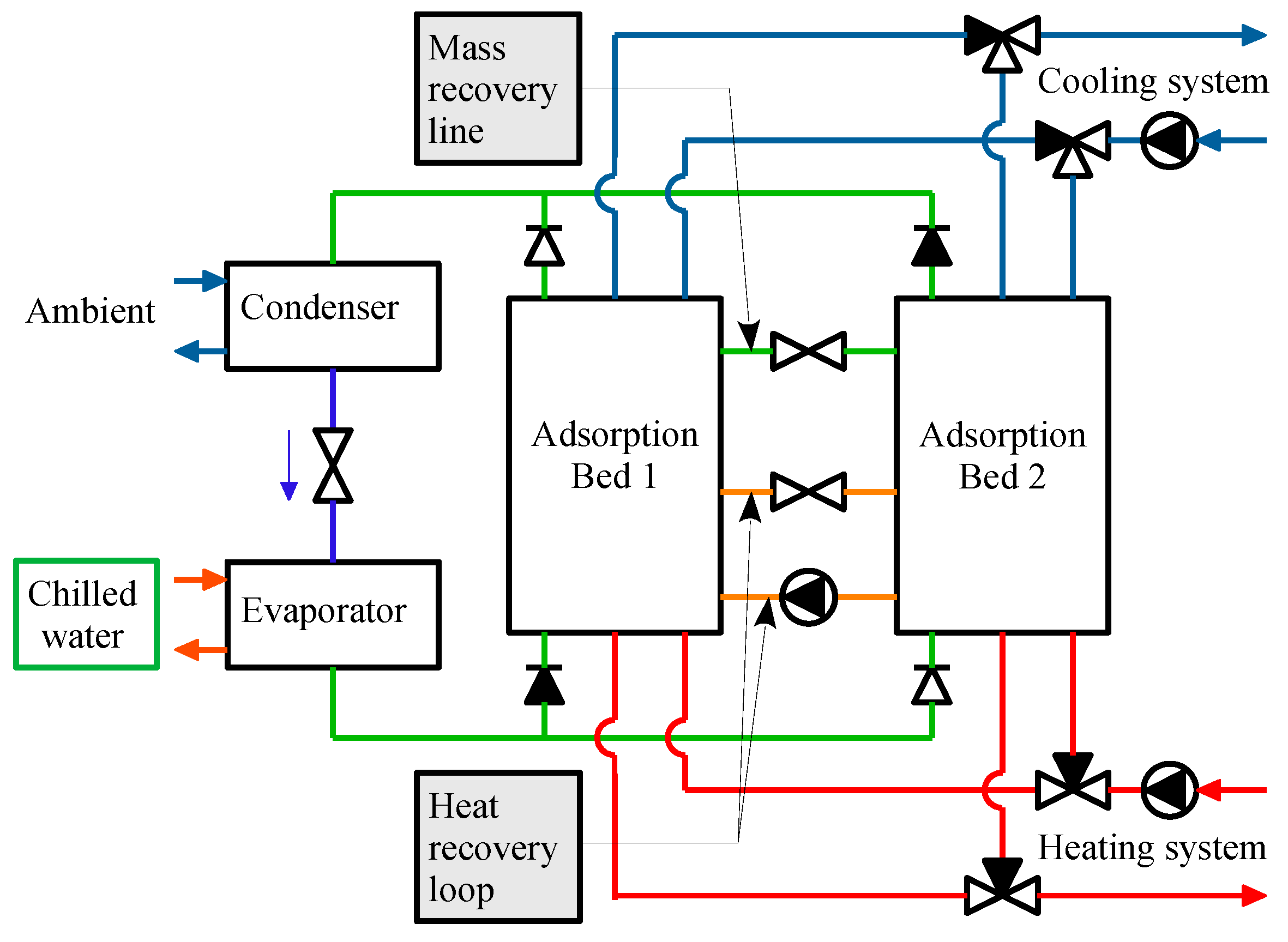
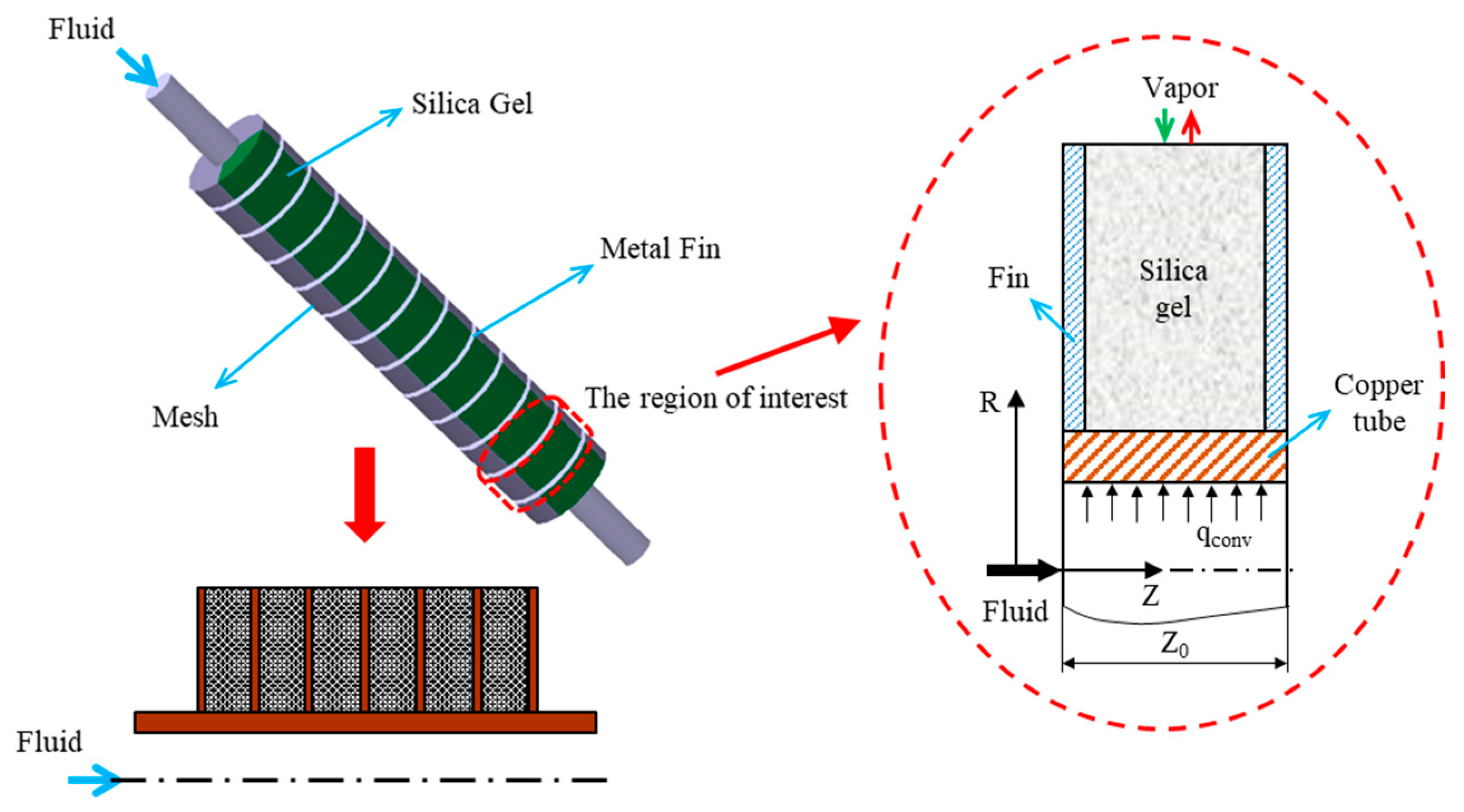
2. Numerical Analysis
2.1. Assumptions
- The adsorbent particles are all spherical with uniform size and porosity.
- The refrigerant vapor is an ideal gas while the adsorbed phase is a liquid.
- The thermo-physical properties of materials are constant except for the density of the refrigerant gas.
- The adsorbed and vapor phases are in local thermal equilibrium.
- The flow in the adsorption bed is axisymmetric.
- There is no heat loss through the chamber wall to the environment.
- The condenser and evaporator are idealised with a constant pressure and temperature during all processes.
- The thermochemical, kinematic and potential exergy are neglected.
- Neglecting the heat losses in the ducts and valves.
- The refrigerant is not to be sub-cooled in the condenser and not to be super-heated in the evaporator.
- The exergy destroyed in the metallic parts of the condenser/evaporator and in the secondary heat transfer fluids are negligible.
- The process in the expansion valve is considered to be isenthalpic.
2.2. Energy Analysis
2.3. Exergy Analysis
2.4. Performance Indices
3. Results and Discussion
3.1. Effect of Recovery Strategy
3.1.1. Basic Cycle
3.1.2. Mass Recovery Cycle
3.1.3. Heat Recovery Cycle
3.1.4. Combined Heat and Mass Recovery Cycle
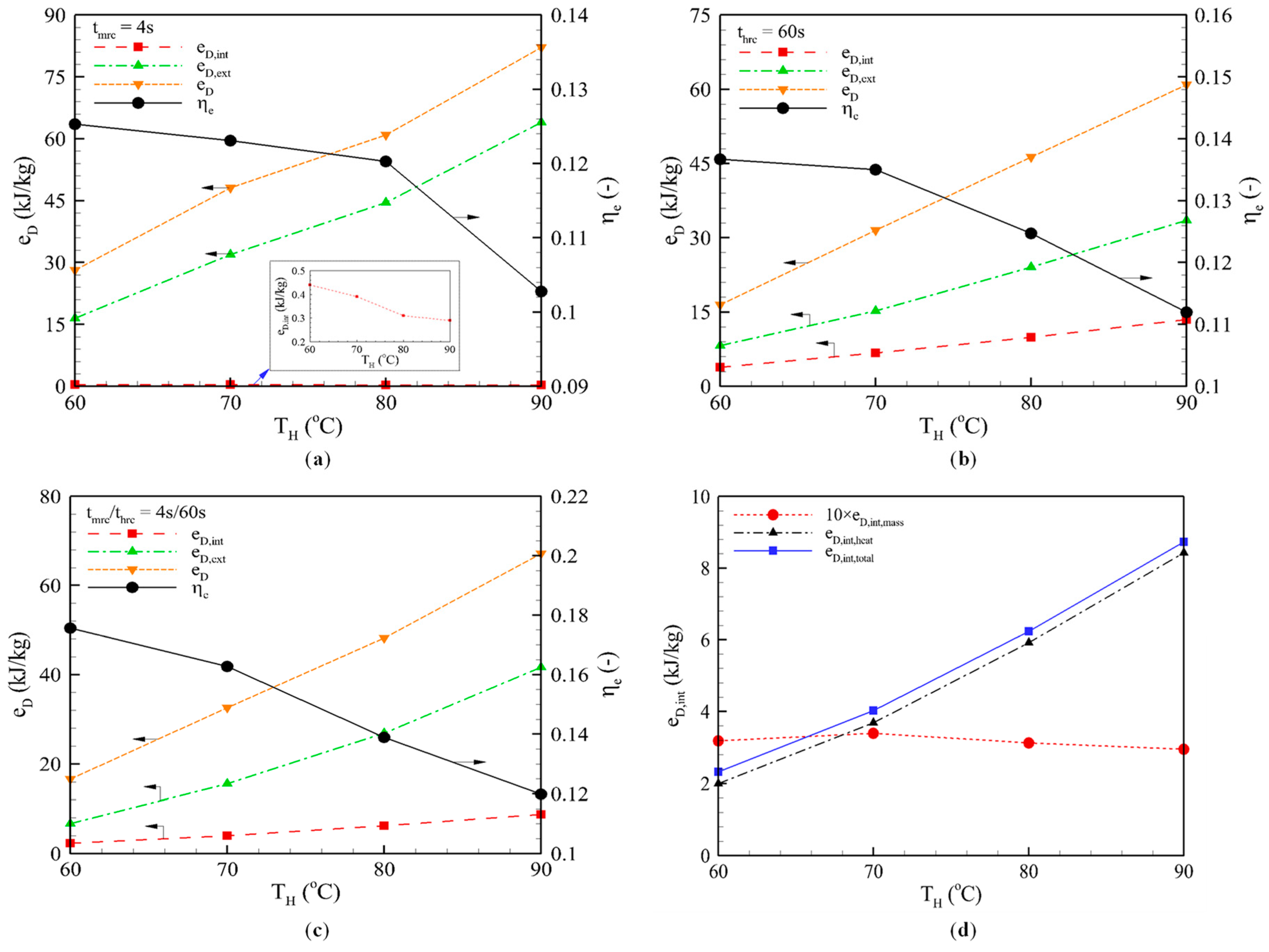
3.2. Effect of Heating Temperature
3.2.1. Mass Recovery Cycle
3.2.2. Heat Recovery Cycle
3.2.3. Combined Heat and Mass Recovery Cycle
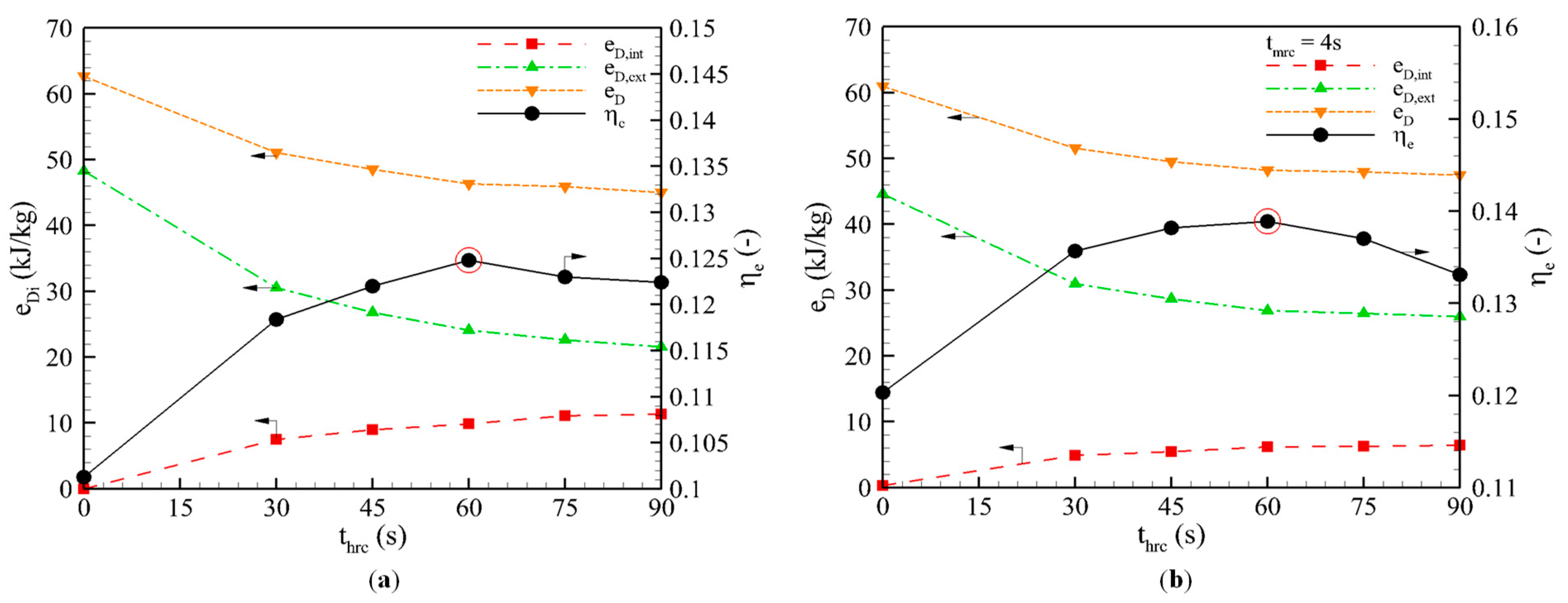
3.3. Effect of Heat Recovery Time
3.3.1. Heat Recovery Cycle
3.3.2. Combined Heat and Mass Recovery Cycle
4. Conclusions
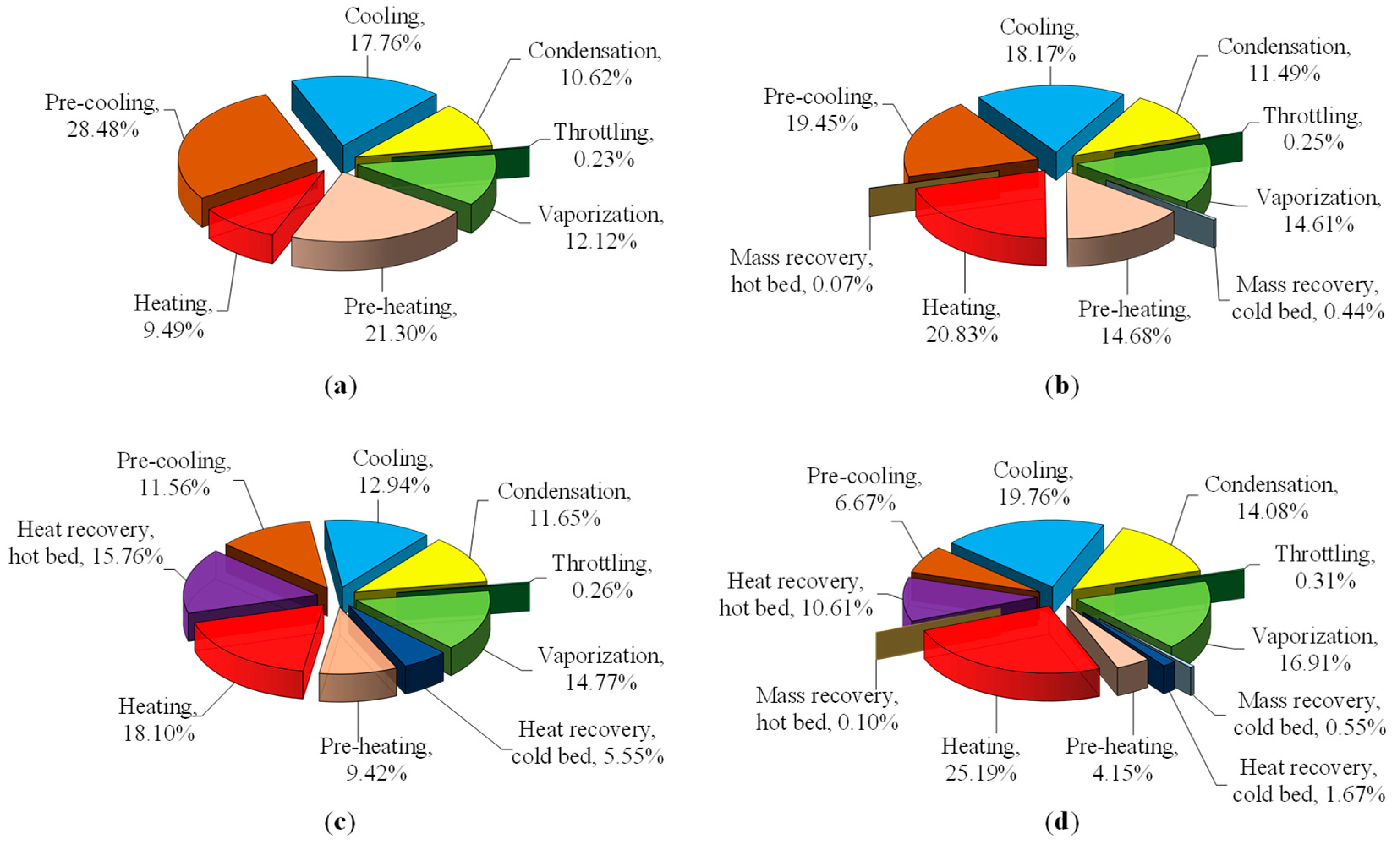
- Mass recovery cycle: The shorter pre-heating and pre-cooling phases, and the larger amount of circulating refrigerant, reduced the external exergy losses to 44.57 kJ/kg, but increased eD,other to 16.06 kJ/kg, which corresponds to −7.68% and +11.53%, respectively, compared to the basic cycle. Overall, the total exergy losses decreased to 60.95 kJ/kg (−2.76%). As the temperature increased, the total exergy loss increased and thus, ηe deceased. This explains why the mass recovery is less influential at low heating temperatures.
- Heat recovery cycle: The external loss (eD,ext = 24.09 kJ/kg) was reduced to half of the basic cycle (48.28 kJ/kg) and the internal loss, eD,int = 9.87 kJ/kg, was about half of the external loss. The total exergy losses, eD = 46.31 kJ/kg, were equal to one-third of the basic cycle. As a consequence, the ηe was significantly enhanced, to 23.20%. The ηe showed an optimum value of 0.1248 at thrc = 60 s, and both the internal and external exergy losses increased as the heating temperature increased.
- Combined heat and mass recovery cycle: The increase in external exergy losses was compensated by the decrease in internal exergy losses, and thus, the total loss was slightly higher than the heat recovery cycle. However, the useful exergy had a remarkable improvement (17.8%, from 6.60 to 7.77 kJ/kg), which resulted in 11.30% enhancement of ηe = 0.1389 compared to the heat recovery cycle (ηe = 0.1248). The enhancement is much clearer when compared to the basic.
- cycle (ηe = 0.1013) with 37.12%. The dependency on heat recovery time and heating temperature was similar to the observation of the individual mass recovery and heat recovery cycles.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |
| cp | Specific heat (J/kg K) |
| dp | Particle diameter (μm) |
| D | Diameter (mm) |
| E | Exergy (J) |
| e | Specific exergy (kJ/kg) |
| ΔH | Heat of adsorption (J/kg) |
| h | Heat transfer coefficient (W/m2 K) |
| k | Thermal conductivity (W/m K) |
| Lo | Length (mm) |
| ṁ | Mass flow rate (kg/s) |
| P | Pressure (Pa) |
| Q | Heat (J) |
| q | Water uptake (kg/kg) |
| S | Entropy (J/K) |
| T | Temperature (K) |
| U | Internal energy (J) |
| V | Volume (m3) |
| t | Time (s) |
| u | Velocity (m/s) |
| Zo | Fin pitch (mm) |
| Greek symbols | |
| δ | Fin thickness (mm) |
| ε | Porosity (-) |
| η | Exergy efficiency (-) |
| ρ | Density (kg/m3) |
| ψ | Mass exergy (J) |
| Subscripts | |
| a | Adsorbed vapor |
| bed | Adsorbent bed |
| con | Condenser |
| cool | Cooling process |
| cycle | Cycle |
| D | Destruction |
| ext | External |
| eva | Evaporator |
| H | Heating fluid |
| heat | Heating |
| hrc | Heat recovery |
| i | Inner tube diameter |
| in | Inlet |
| int | Internal |
| L | Cooling fluid |
| l | Liquid phase |
| m | Metallic metal |
| mrc | Mass recovery |
| o | Outer tube diameter |
| other | Other |
| out | Outlet |
| prec | Pre-cooling |
| preh | Pre-heating |
| s | Solid adsorbent |
| v | Vapor |
| val | Valve |
References
- Pons, M.; Poyelle, F. Adsorptive machines with advanced cycles for heat pumping or cooling applications. Int. J. Refrig. 1999, 22, 27–37. [Google Scholar] [CrossRef]
- Pan, Q.W.; Wang, R.Z.; Wang, L.W. Comparison of different kinds of heat recoveries applied in adsorption refrigeration system. Int. J. Refrig. 2015, 55, 37–48. [Google Scholar] [CrossRef]
- Chekirou, W.; Boukheit, N.; Karaali, A. Heat recovery process in an adsorption refrigeration machine. Int. J. Hydrogen Energy 2016, 41, 7146–7157. [Google Scholar] [CrossRef]
- Wang, R.Z. Performance improvement of adsorption cooling by heat and mass recovery operation. Int. J. Refrig. 2001, 24, 602–611. [Google Scholar] [CrossRef]
- Akahira, A.; Alam, K.C.A.; Hamamoto, Y.; Akisawa, A.; Kashiwagi, T. Mass recovery adsorption refrigeration cycle—Improving cooling capacity. Int. J. Refrig. 2004, 27, 225–234. [Google Scholar] [CrossRef]
- Pan, Q.; Wang, R.; Lu, Z.; Wang, L. Thermodynamic analysis and performance simulation of different kinds of mass recovery processes applied in adsorption refrigeration system. HVAC R. Res. 2014, 20, 311–319. [Google Scholar] [CrossRef]
- Ghilen, N.; Gabsi, S.; Benelmir, R.; Ganaoui, M.E. Performance Simulation of Two-Bed Adsorption Refrigeration Chiller with Mass Recovery. JFREA 2017, 7, 2. [Google Scholar] [CrossRef]
- Qu, T.F.; Wang, R.Z.; Wang, W. Study on heat and mass recovery in adsorption refrigeration cycles. Appl. Therm. Eng. 2001, 21, 439–452. [Google Scholar] [CrossRef]
- Leong, K.C.; Liu, Y. Numerical study of a combined heat and mass recovery adsorption cooling cycle. Int. J. Heat Mass Transf. 2004, 47, 4761–4770. [Google Scholar] [CrossRef]
- Chen, C.J.; Wang, R.Z.; Xia, Z.Z.; Kiplagat, J.K.; Lu, Z.S. Study on a compact silica gel–water adsorption chiller without vacuum valves: Design and experimental study. Appl. Energy 2010, 87, 2673–2681. [Google Scholar] [CrossRef]
- Duong, X.Q.; Cao, N.V.; Chung, J.D. Heat Recovery Time of Adsorption Cooling System. IJACR 2018, 26, 1850014. [Google Scholar] [CrossRef]
- Duong, X.Q.; Cao, N.V.; Hong, S.W.; Ahn, S.H.; Chung, J.D. Numerical Study on the Combined Heat and Mass Recovery Adsorption Cooling Cycle. Energy Technol. 2018, 6, 296–305. [Google Scholar] [CrossRef]
- Meunier, F.; Kaushik, S.C.; Neveu, P.; Poyelle, F. A comparative thermodynamic study of sorption systems: Second law analysis. Int. J. Refrig. 1996, 19, 414–421. [Google Scholar] [CrossRef]
- Meunier, F.; Poyelle, F.; LeVan, M.D. Second-law analysis of adsorptive refrigeration cycles: The role of thermal coupling entropy production. Appl. Therm. Eng. 1997, 17, 43–55. [Google Scholar] [CrossRef]
- Ogueke, N.; Ndeke, C. Exergy based performance analysis of a solid adsorption solar refrigerator. Int. J. Renew. Energy Res. 2014, 4, 363–370. [Google Scholar]
- Dincer, I.; Rosen, M.A. Exergy Analysis of Heating, Refrigerating and Air Conditioning: Methods and Applications; Elsevier Science: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Vasilescu, E.E.; Boussehain, R.; Feidt, M.L. Exergy analysis of an adsorption refrigeration machine. Int. J. Exergy 2007, 4. [Google Scholar] [CrossRef]
- Baiju, V.; Muraleedharan, C. Energy and exergy analysis of solar hybrid adsorption refrigeration system. Int. J. Sustain. Eng. 2013, 6, 289–300. [Google Scholar] [CrossRef]
- Sharifzadeh, M.; Ghazikhani, M.; Niazmand, H. Temporal exergy analysis of adsorption cooling system by developing non-flow exergy function. Appl. Therm. Eng. 2018, 139, 409–418. [Google Scholar] [CrossRef]
- Cao, N.V.; Chung, J.D. Exergy Analysis of Adsorption Cooling Systems Based on Numerical Simulation. Energy Technol. 2019, 7, 153–166. [Google Scholar] [CrossRef]
- Baker, D.K. Thermodynamic limits to thermal regeneration in adsorption cooling cycles. Int. J. Refrig. 2008, 31, 55–64. [Google Scholar] [CrossRef]
- Hong, S.W.; Kwon, O.K.; Chung, J.D. Effect of the switching time on the performance of an adsorption chiller. J. Mech. Sci. Technol. 2016, 30, 2387–2395. [Google Scholar] [CrossRef]
- Khan, M.Z.I.; Saha, B.B.; Alam, K.C.A.; Akisawa, A.; Kashiwagi, T. Study on solar/waste heat driven multi-bed adsorption chiller with mass recovery. Renew. Energy 2007, 32, 365–381. [Google Scholar] [CrossRef]
| Parameter | Symbol | Values |
|---|---|---|
| Fin Pitch | Zo | 3 mm |
| Fin Height | Lo | 10 mm |
| Fin Thickness | δ | 0.4 mm |
| Inner Diameter of Metal Tube | Di | 10 mm |
| Outer Diameter of Metal Tube | Do | 12 mm |
| Particle Diameter | dp | 200 μm |
| Evaporator Temperature | Teva | 15 °C |
| Condenser Temperature | Tcon | 30 °C |
| Cooling Temperature | TL | 30 °C |
| Heating Temperature | TH | 60 °C~90 °C |
| Average Fluid Velocity | uf | 1 m/s |
| Density of Adsorbent | ρb | 761 kg/m3 |
| Specific Heat of Adsorbent | Cp.b | 920 J/kgK |
| Thermal Conductivity of Adsorbent | kb | 0.198 W/mK |
| Heat of Adsorption | ΔH | 2.76 × 106 J/kg |
| Porosity of the Particle | εp | 0.43 |
| Porosity of the Bed | εb | 0.36 |
| Cycle Time | tcycle | 840 s |
| Mass Recovery Time | tmrc | 4 s |
| Heat Recovery Time | thrc | ≤ 90 s |
| Cycle | thrc (s) | tmrc (s) | Specific Exergy (kJ/kg) | ηe (−) | ||||
|---|---|---|---|---|---|---|---|---|
| eD,int | eD,ext | eD,other | eD | eeva | ||||
| Basic Cycle | 0 | 0 | 0.00 | 48.28 | 14.40 | 62.68 | 7.06 | 0.1013 |
| Mass Recovery Cycle | 0 | 4 | 0.31 | 44.57 | 16.06 | 60.95 | 8.33 | 0.1203 |
| Heat Recovery Cycle | 60 | 0 | 9.87 | 24.09 | 12.35 | 46.31 | 6.60 | 0.1248 |
| Combined Heat and Mass Recovery Cycle | 60 | 4 | 6.23 | 26.88 | 15.09 | 48.19 | 7.77 | 0.1389 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, N.V.; Duong, X.Q.; Lee, W.S.; Park, M.Y.; Lee, S.S.; Chung, J.D. Exergy Analysis of Advanced Adsorption Cooling Cycles. Entropy 2020, 22, 1082. https://doi.org/10.3390/e22101082
Cao NV, Duong XQ, Lee WS, Park MY, Lee SS, Chung JD. Exergy Analysis of Advanced Adsorption Cooling Cycles. Entropy. 2020; 22(10):1082. https://doi.org/10.3390/e22101082
Chicago/Turabian StyleCao, Ngoc Vi, Xuan Quang Duong, Woo Su Lee, Moon Yong Park, Seung Soo Lee, and Jae Dong Chung. 2020. "Exergy Analysis of Advanced Adsorption Cooling Cycles" Entropy 22, no. 10: 1082. https://doi.org/10.3390/e22101082
APA StyleCao, N. V., Duong, X. Q., Lee, W. S., Park, M. Y., Lee, S. S., & Chung, J. D. (2020). Exergy Analysis of Advanced Adsorption Cooling Cycles. Entropy, 22(10), 1082. https://doi.org/10.3390/e22101082





