Open-Destination Measurement-Device-Independent Quantum Key Distribution Network
Abstract
1. Introduction
2. Open-Destination MDI-QKD Network
2.1. Protocol
- Step. 1
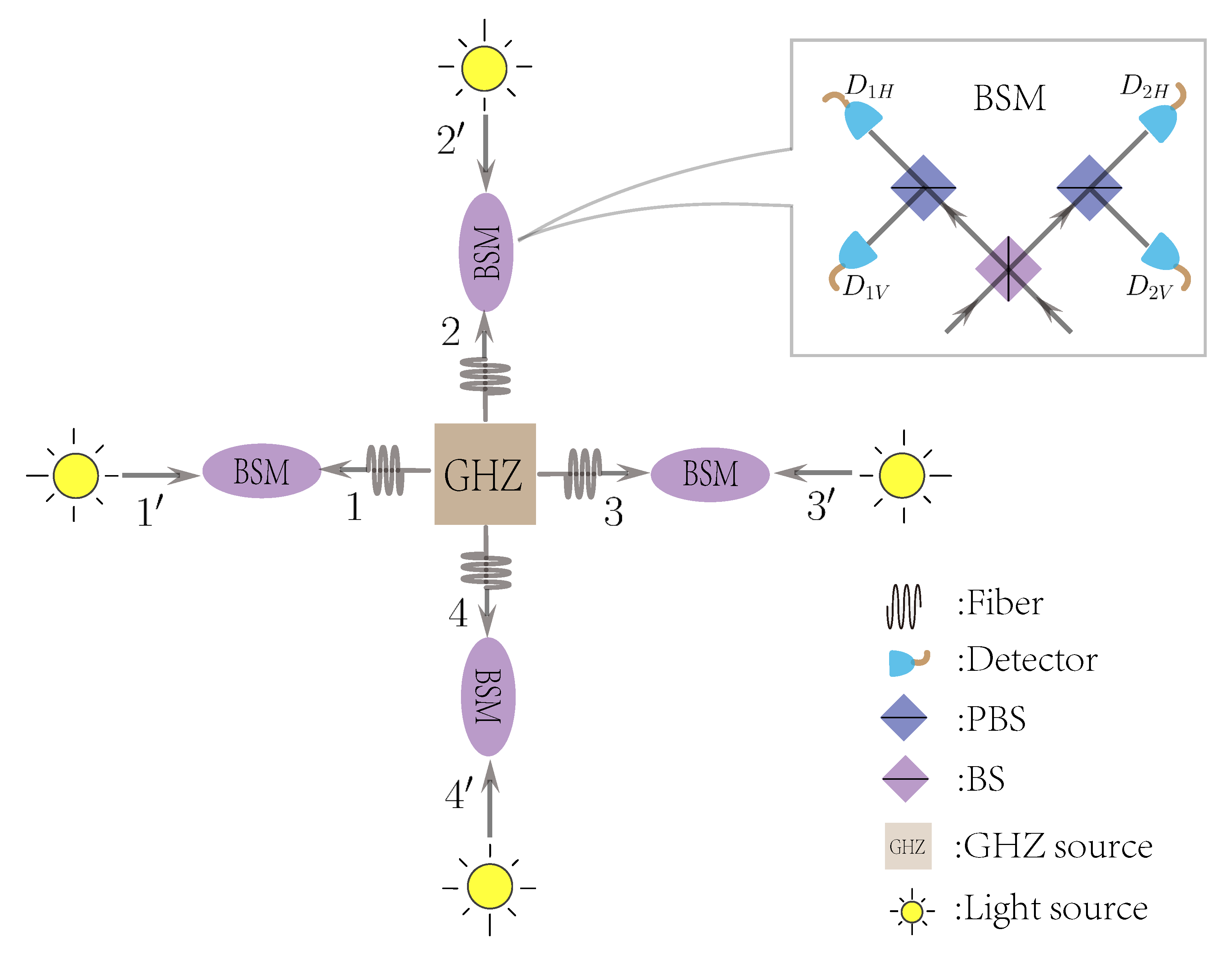
- Preparation: A third party, which may be untrusted, prepares N-partite GHZ statewhere and denote two eigenstates of the computational basis Z. All users prepare BB84 polarization states, i.e., , , , and with being the two eigenstates of the basis X. The third party and all users distribute the prepared quantum states to their relays, which may also be untrusted.
- Step. 2
- Measurement: The relays perform Bell state measurements (BSMs). When using linear optical setups, only two outcomes related to projections on can be distinguished.
- Step. 3
- Announcement: All relays announce their successful BSM results among a public classical authenticated channel. The two communication users announce their photons bases, and other users announce their states prepared in the X basis.
- Step. 4
- Sifting: The two communication user keep the strings where all the relays get successful BSM results and other users use X bases. Then, they discard the strings where different preparation bases are used. To guarantee their strings to be correctly correlated, one of the two users flip or not flip his/her bit according to the corresponding BSM results and other users’ prepared states (see Appendix A for details). Then, the two users obtain the raw key bits.
- Step. 5
- Post-processing: The two communication users estimate the quantum phase error and quantum bit error rate (QBER) in Z and X bases, according to which they further perform error correction and privacy amplification to extract correct and secure keys.
2.2. Correctness and Security Analysis
2.3. Key Generation Rate
2.4. Comparison with the Standard MDI-QKD
3. Numerical Simulation
4. Generalization to the (N,C) Case
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Sifting Procedure of the (4,2) Case

| State of System | BSM Result on Systems | POVM on System k |
|---|---|---|
| Bell | BSM Result 1 | BSM Result 2 | BSM |
|---|---|---|---|
| Basis | ||
|---|---|---|
| Z-basis | No Flip | No Flip |
| X-basis | No Flip | Flip |
Appendix B. Detector Analysis

| f | ||||
|---|---|---|---|---|
Appendix C. Simulation for (4,2)-Scenario

References
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computer System and Signal Processing; IEEE: New York, NY, USA, 1984; p. 175. [Google Scholar]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661–663. [Google Scholar] [CrossRef] [PubMed]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- Elliott, C. The DARPA quantum network. In Quantum Communications and Cryptography; CRC Press: Boca Raton, FL, USA, 2005; pp. 83–102. [Google Scholar]
- Peev, M.; Pacher, C.; Alléaume, R.; Barreiro, C.; Bouda, J.; Boxleitner, W.; Debuisschert, T.; Diamanti, E.; Dianati, M.; Dynes, J.; et al. The SECOQC quantum key distribution network in Vienna. New J. Phys. 2009, 11, 075001. [Google Scholar] [CrossRef]
- Chen, T.Y.; Wang, J.; Liang, H.; Liu, W.Y.; Liu, Y.; Jiang, X.; Wang, Y.; Wan, X.; Cai, W.Q.; Ju, L.; et al. Metropolitan all-pass and inter-city quantum communication network. Opt. Express 2010, 18, 27217–27225. [Google Scholar] [CrossRef]
- Sasaki, M.; Fujiwara, M.; Ishizuka, H.; Klaus, W.; Wakui, K.; Takeoka, M.; Miki, S.; Yamashita, T.; Wang, Z.; Tanaka, A.; et al. Field test of quantum key distribution in the Tokyo QKD Network. Opt. Express 2011, 19, 10387–10409. [Google Scholar] [CrossRef]
- Fröhlich, B.; Dynes, J.F.; Lucamarini, M.; Sharpe, A.W.; Yuan, Z.; Shields, A.J. A quantum access network. Nature 2013, 501, 69. [Google Scholar] [CrossRef]
- Qiu, J. Quantum communications leap out of the lab. Nature (London) 2014, 508, 441. [Google Scholar] [CrossRef]
- Liao, S.K.; Cai, W.Q.; Handsteiner, J.; Liu, B.; Yin, J.; Zhang, L.; Rauch, D.; Fink, M.; Ren, J.G.; Liu, W.Y.; et al. Satellite-Relayed Intercontinental Quantum Network. Phys. Rev. Lett. 2018, 120, 030501. [Google Scholar] [CrossRef]
- Qi, B.; Fung, C.H.F.; Lo, H.K.; Ma, X. Time-shift Attack in Practical Quantum Cryptosystems. Quantum Inf. Comput. 2007, 7, 073. [Google Scholar]
- Zhao, Y.; Fung, C.H.F.; Qi, B.; Chen, C.; Lo, H.K. Quantum hacking: Experimental demonstration of time-shift attack against practical quantum-key-distribution systems. Phys. Rev. A 2008, 78, 042333. [Google Scholar] [CrossRef]
- Lydersen, L.; Wiechers, C.; Wittmann, C.; Elser, D.; Skaar, J.; Makarov, V. Hacking commercial quantum cryptography systems by tailored bright illumination. Nat. Photonics 2010, 4, 686–689. [Google Scholar] [CrossRef]
- Gerhardt, I.; Liu, Q.; Lamas-Linares, A.; Skaar, J.; Kurtsiefer, C.; Makarov, V. Full-field implementation of a perfect eavesdropper on a quantum cryptography system. Nat. Commun. 2011, 2, 349. [Google Scholar] [CrossRef] [PubMed]
- Weier, H.; Krauss, H.; Rau, M.; Fürst, M.; Nauerth, S.; Weinfurter, H. Quantum eavesdropping without interception: An attack exploiting the dead time of single-photon detectors. New J. Phys. 2011, 13, 073024. [Google Scholar] [CrossRef]
- Lo, H.K.; Curty, M.; Qi, B. Measurement-Device-Independent Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130503. [Google Scholar] [CrossRef]
- Braunstein, S.L.; Pirandola, S. Side-Channel-Free Quantum Key Distribution. Phys. Rev. Lett. 2012, 108, 130502. [Google Scholar] [CrossRef]
- Xu, F.; Curty, M.; Qi, B.; Qian, L.; Lo, H.K. Discrete and continuous variables for measurement-device-independent quantum cryptography. Nat. Photonics 2015, 9, 772. [Google Scholar] [CrossRef]
- Pirandola, S.; Ottaviani, C.; Spedalieri, G.; Weedbrook, C.; Braunstein, S.L.; Lloyd, S.; Gehring, T.; Jacobsen, C.S.; Andersen, U.L. Reply to Discrete and continuous variables for measurement-device-independent quantum cryptography. Nat. Photonics 2015, 9, 773. [Google Scholar] [CrossRef]
- Tang, Z.; Wei, K.; Bedroya, O.; Qian, L.; Lo, H.K. Experimental measurement-device-independent quantum key distribution with imperfect sources. Phys. Rev. A 2016, 93, 042308. [Google Scholar] [CrossRef]
- Epping, M.; Kampermann, H.; Macchiavello, C.; Bruß, D. Multi-partite entanglement can speed up quantum key distribution in networks. New J. Phys. 2017, 19, 093012. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, Y.A.; Zhang, A.N.; Yang, T.; Briegel, H.J.; Pan, J.W. Experimental demonstration of five-photon entanglement and open-destination teleportation. Nature 2004, 430, 54–58. [Google Scholar] [CrossRef] [PubMed]
- Bose, S.; Vedral, V.; Knight, P.L. Multiparticle generalization of entanglement swapping. Phys. Rev. A 1998, 57, 822–829. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- Hwang, W.Y. Quantum Key Distribution with High Loss: Toward Global Secure Communication. Phys. Rev. Lett. 2003, 91, 057901. [Google Scholar] [CrossRef]
- Lo, H.K.; Ma, X.; Chen, K. Decoy State Quantum Key Distribution. Phys. Rev. Lett. 2005, 94, 230504. [Google Scholar] [CrossRef]
- Wang, X.B. Beating the Photon-Number-Splitting Attack in Practical Quantum Cryptography. Phys. Rev. Lett. 2005, 94, 230503. [Google Scholar] [CrossRef]
- Xu, F.; Qi, B.; Liao, Z.; Lo, H.K. Long distance measurement-device-independent quantum key distribution with entangled photon sources. Appl. Phys. Lett. 2013, 103, 061101. [Google Scholar] [CrossRef]
- Koashi, M.; Winter, A. Monogamy of quantum entanglement and other correlations. Phys. Rev. A 2004, 69, 022309. [Google Scholar] [CrossRef]
- Osborne, T.J.; Verstraete, F. General Monogamy Inequality for Bipartite Qubit Entanglement. Phys. Rev. Lett. 2006, 96, 220503. [Google Scholar] [CrossRef]
- Ou, Y.C.; Fan, H.; Fei, S.M. Proper monogamy inequality for arbitrary pure quantum states. Phys. Rev. A 2008, 78, 012311. [Google Scholar] [CrossRef]
- Gottesman, D.; Lo, H.K.; Lütkenhaus, N.; Preskill, J. Security of quantum key distribution with imperfect devices. Quantum Inf. Comput. 2004, 4, 325. [Google Scholar]
- Chen, K.; Lo, H.K. Multi-partite quantum cryptographic protocols with noisy GHZ states. Quantum Inf. Comput. 2007, 7, 689. [Google Scholar]
- Tang, Y.L.; Yin, H.L.; Chen, S.J.; Liu, Y.; Zhang, W.J.; Jiang, X.; Zhang, L.; Wang, J.; You, L.X.; Guan, J.Y.; et al. Measurement-Device-Independent Quantum Key Distribution over 200 km. Phys. Rev. Lett. 2014, 113, 190501. [Google Scholar] [CrossRef] [PubMed]
- Curty, M.; Xu, F.; Cui, W.; Lim, C.C.W.; Tamaki, K.; Lo, H.K. Finite-key analysis for measurement-device- independent quantum key distribution. Nat. Commun. 2014, 5, 3732. [Google Scholar] [CrossRef]
- Xu, F.; Xu, H.; Lo, H.K. Protocol choice and parameter optimization in decoy-state measurement-device- independent quantum key distribution. Phys. Rev. A 2014, 89, 052333. [Google Scholar] [CrossRef]
- Chen, K.; Lo, H.K. Conference key agreement and quantum sharing of classical secrets with noisy GHZ states. In Proceedings of the International Symposium on Information Theory (ISIT 2005), Adelaide, SA, Australia, 4–9 September 2005; pp. 1607–1611. [Google Scholar] [CrossRef]
- Fu, Y.; Yin, H.L.; Chen, T.Y.; Chen, Z.B. Long-Distance Measurement-Device-Independent Multiparty Quantum Communication. Phys. Rev. Lett. 2015, 114, 090501. [Google Scholar] [CrossRef]
- Zhao, S.; Zeng, P.; Cao, W.F.; Xu, X.Y.; Zhen, Y.Z.; Ma, X.; Li, L.; Liu, N.L.; Chen, K. Phase-Matching Quantum Cryptographic Conferencing. Phys. Rev. Appl. 2020, 14, 024010. [Google Scholar] [CrossRef]
- Hillery, M.; Bužek, V.; Berthiaume, A. Quantum secret sharing. Phys. Rev. A 1999, 59, 1829–1834. [Google Scholar] [CrossRef]
- Cleve, R.; Gottesman, D.; Lo, H.K. How to Share a Quantum Secret. Phys. Rev. Lett. 1999, 83, 648–651. [Google Scholar] [CrossRef]
- Chen, Y.A.; Zhang, A.N.; Zhao, Z.; Zhou, X.Q.; Lu, C.Y.; Peng, C.Z.; Yang, T.; Pan, J.W. Experimental Quantum Secret Sharing and Third-Man Quantum Cryptography. Phys. Rev. Lett. 2005, 95, 200502. [Google Scholar] [CrossRef]
- Lo, H.K.; Chau, H.F. Unconditional security of quantum key distribution over arbitrarily long distances. Science 1999, 283, 2050–2056. [Google Scholar] [CrossRef] [PubMed]
- Shor, P.W.; Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 2000, 85, 441. [Google Scholar] [CrossRef] [PubMed]
- Maneva, E.N.; Smolin, J.A. Improved two-party and multi-party purification protocols. Contemp. Math. 2002, 305, 203–212. [Google Scholar]
- Wang, W.; Xu, F.; Lo, H.K. Asymmetric Protocols for Scalable High-Rate Measurement-Device-Independent Quantum Key Distribution Networks. Phys. Rev. X 2019, 9, 041012. [Google Scholar] [CrossRef]

| GHZ | BSM Result 1 | BSM Result 2 | BSM Result 3 | GHZ Analyzer |
|---|---|---|---|---|
| () | () | |||
| () | () | |||
| () | () | |||
| () | () | |||
| () | () | |||
| () | () | |||
| () | () | |||
| () | () |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.-F.; Zhen, Y.-Z.; Zheng, Y.-L.; Zhao, S.; Xu, F.; Li, L.; Chen, Z.-B.; Liu, N.-L.; Chen, K. Open-Destination Measurement-Device-Independent Quantum Key Distribution Network. Entropy 2020, 22, 1083. https://doi.org/10.3390/e22101083
Cao W-F, Zhen Y-Z, Zheng Y-L, Zhao S, Xu F, Li L, Chen Z-B, Liu N-L, Chen K. Open-Destination Measurement-Device-Independent Quantum Key Distribution Network. Entropy. 2020; 22(10):1083. https://doi.org/10.3390/e22101083
Chicago/Turabian StyleCao, Wen-Fei, Yi-Zheng Zhen, Yu-Lin Zheng, Shuai Zhao, Feihu Xu, Li Li, Zeng-Bing Chen, Nai-Le Liu, and Kai Chen. 2020. "Open-Destination Measurement-Device-Independent Quantum Key Distribution Network" Entropy 22, no. 10: 1083. https://doi.org/10.3390/e22101083
APA StyleCao, W.-F., Zhen, Y.-Z., Zheng, Y.-L., Zhao, S., Xu, F., Li, L., Chen, Z.-B., Liu, N.-L., & Chen, K. (2020). Open-Destination Measurement-Device-Independent Quantum Key Distribution Network. Entropy, 22(10), 1083. https://doi.org/10.3390/e22101083






