1. Introduction
It is known that, in certain approximations, Einstein equations can be written in the form of Maxwell equations. In linearized gravity, for instance, the Riemann tensor is
which, except for the presence of second order derivatives instead of those of first order, bears a similarity to the electromagnetic field tensor
The algebraic and differential identities that these tensors satisfy are also similar. For the electromagnetic field we have
while for the Riemann tensor we find
The last equation of (
4) goes under the name of Bianchi identities. The tensors
and
also appear in the field equations and characterize the fields completely [
1]. By separating the “electric” and “magnetic” components according to
and
and using (
3) and (
4), we can write the field equations
in the form of Maxwell equations [
1]
In addition, the wave equations and are also satisfied.
The formal similarities just outlined refer to a vacuum. Other similarities and versions of “gravitoelectromagnetism” (GEM) do, however, appear when the interaction of, say, a scalar particle with gravity is considered. In the minimal coupling approximation, a scalar particle of mass
m obeys the covariant Klein–Gordon equation
which, in the weak field approximation
where
is the Minkowski metric, and on applying the Lanczos–DeDonder condition
becomes
Units
are used and the notation is as in [
2]. In particular, partial derivatives with respect to a variable
are interchangeably indicated by
, or by a comma followed by
.
is a covariant derivative. Indices are lowered and raised by means of the metric tensor
,
and gravitational contributions are kept only up to
.
Equation (
11) has the exact solution [
3,
4,
5]
where
is a plane wave solution of the free Klein–Gordon equation,
P is some fixed base event that may be omitted for simplicity in what follows and
Two-point functions such as (
14) belong to the family of world-functions introduced into Riemannian geometry by Ruse [
6] and Synge [
7] and are used in general relativity to study the curvature structure of space-time. Here they also introduce elements of the topology of space-time, as can be seen by taking the derivatives with respect to
z of the function
defined by
which coincides with (
14). One obtains
where
is the linearized Riemann tensor (
1). It follows from (
16) that
is not single-valued, and that after a gauge transformation,
satisfies the equations
that
identically, and that
because of (
17), while the equation
holds everywhere. Therefore,
is regular everywhere, but
is singular because the double derivatives of
do not commute. From (
16) one gets
that can be solved to yield
. Notice also that
and that again
. Equations (
19) and (
20) are Maxwell-type equations, and (
18) is similar to the equation satisfied by the vector potential in electromagnetism. In essence, the scalar particle of mass
m “sees” a gravitational field that, under the circumstances discussed in
Section 6, is vectorial, rather than tensorial, and acquires a generalized momentum that generates the correct geometrical optics and index of refraction, as shown below. The new quantities
contain the original particle momentum
. They therefore acquire, upon quantization, the characteristics of “quasiparticles”. This alternate procedure also brings to the fore the elusive “electromagnetic” character of gravity and the “electromagnetic” properties so acquired persist at higher order in
. In fact, to any order
n of
, the solution of (
9) can be written as
where
is the operator obtained from (
13) by replacing
with
. In what follows, the approximations are always carried out to
for simplicity.
The fundamental reason for the appearance of gravitational quasiparticles resides in (
12) and (
13) and has a geometrical explanation. Equations (
12) and (
13) represent a space-time transformation of the vacuum that makes the ground state degenerate, breaks the continuous symmetry of the system and leads to the phenomenon of condensation. This follows from the well-known fact that the original, rotation-invariant system
, transported along a closed path
bounding a small surface
, changes, because of the curvature of space-time, by
where
is the angular momentum operator and
Equation (
22) can be obtained by applying Stokes’ theorem to (
12) and (
13). The rotational invariant system
therefore acquires a privileged direction (that of rotation), on being translated along the closed path
in curved space-time. The direction of rotation due to
breaks the original symmetry. The new space-time-dependent ground state (
12) reflects the lack of symmetry under rotation. Thus the topological singularity that appears in
is supplied by the geometry of space-time itself.
It is possible to construct more complex solutions of (
11), such as a closed rectangular loop, or ring, by combining two vortex-type solutions (
12) and (
13) with opposite directions, and in general, by linear superposition of the solution found. In short, the curvature of space-time breaks the original symmetry by introducing preferred directions.
There are consequences for the scalar particle and the gravitational field. Notwithstanding the use of a quantum wave equation for
, the fields
and
are classical. The transformation (
12) and (
13) does not affect only the field
, but the other fields as well, as shown in
Section 2,
Section 3,
Section 4 and
Section 5 where dispersion relations, geometrical optics, particle motion and the appearance of quasiparticles are discussed. Initially the fields are represented by
which is classical, and by the field
, which satisfies a quantum equation and has rotational symmetry. Finally, the gravitational field is represented by
which is classical and contains a topological singularity generated by the curvature of space-time, while
, which satisfies a quantum equation, is no longer rotational invariant. This transformation is discussed at length in the following sections together with various aspects of the interaction of
with matter. In
Section 6 we introduce a simple model Lagrangian that illustrates how condensation affects the quantum system considered.
Section 7 and
Section 8 are concerned with statistical aspects of an ensemble of scalar particles in a gravitational background and the origin of a correlation length and alignment per particle, together with analogues of Curie and Bloch laws and spin waves in the ensemble. A summary and conclusions are contained in
Section 9.
Solutions similar to (
12) and (
13) have also been found for particles with spin-2 [
8], spin-1 [
9] and spin-
[
3]. We refer to the original papers for their derivations and discussions regarding minimal coupling terms. The common feature of the solutions given in [
3,
4,
5,
6,
7,
8,
10] is the presence of the term (
23) due to curved space-time.
We report, in particular, the results for spin-2 particles in the following section when discussing geometrical optics.
2. Dispersion Relations, Geometrical Optics and Particle Motion
By using Schroedinger’s logarithmic transformation [
11]
we can pass from the KG Equation (
9) to the quantum Hamilton–Jacobi equation. We find to first order in
where
It is well-known that the Hamilton–Jacobi equation is equivalent to Fresnel’s wave equation in the limit of large frequencies [
11]. However, at smaller or moderate frequencies the complete Equation (
24) should be used. We follow this path. By substituting (
12) into the first term of (
24), we obtain
on account of (
10). This part of (
24) is usually neglected in the limit
. Here it vanishes as a consequence of solution (
12). The remaining terms of (
24) yield the classical Hamilton–Jacobi equation
because
. Equation (
12) is therefore a solution of the more general quantum Equation (
24). It also follows that the particle acquires the generalized “momentum”
that satisfies the dispersion relation
The integral in (
29) vanishes because
is contracted on the antisymmetric tensor in round brackets. The effective mass
is not in general constant. In this connection too we can speak of quasiparticles. The medium in which the scalar particles propagate is here represented by space-time.
By differentiating with respect to
and
where
are the Christoffel symbols, and by differentiating (
28) we obtain the covariant derivative of
This result is independent of any choice of field equations for
. We see from (
32) that, if
follows a geodesic, then
and
. The classical equations of motion are therefore contained in (
32), but it would require the particle described by (
9) to just choose a geodesic, among all the paths allowed to a quantum particle.
We also obtain, from (
24),
, which, in the absence of gravity, gives
, as expected. Remarkably, (
28) is an exact integral of (
32) which can itself be integrated exactly to give the particle’s motion
Higher order approximations to the solution of (
9) can be obtained by using (
21), which plays a dynamical role akin to Feynman’s path integral formula [
10]. In (
21), however, it is the solution itself that is varied by successive approximations, rather than the particle’s path.
In order to gain some insight into the formalism, we derive the geometrical optics approximation for a spin-2 particle. The covariant wave equation for spin-2 particles is
The first order in
, (
34) can be written in the form
where
is the linearized Ricci tensor of the background metric and
is the corresponding Christoffel symbol of the first kind. The solution is
where
From
one constructs the rotation matrices
that satisfy the commutation relations
. The spin-gravity interaction is therefore contained in the term
The solution (
36) is invariant under the gauge transformations
, where
are small quantities of the first order. If, in fact, we choose a closed integration path
, Stokes’ theorem transforms the first three integrals of (
36) into
, where
is the surface bound by
,
is the total angular momentum of the particle and
is the linearized Riemann tensor (
1). For the same path
the integral involving
in (
36) behaves like a gauge term and may therefore be dropped. For the same closed paths, (
36) gives
which obviously is covariant and gauge invariant, and where
satisfies the field-free equation.
Neglecting spin effects [
12,
13], we get from (
36)
The general relativistic deflection of a spin-2 particle in a gravitational field follows immediately from
. By assuming, for simplicity, that the spin-2 particles are massless and propagate along the
z-direction, so that
, and
or
, using plane waves for
and writing
the particle momentum is
It then follows from (
42) that
satisfies the eikonal equation
.
The calculation of the deflection angle is particularly simple to do if the background metric is
where
and
, which is frequently used in gravitational lensing. For this metric,
is given by
The space components of the momentum are therefore
We find
where
is the component of the momentum orthogonal to the direction of propagation of the particles.
Since only phase differences are physical, it is convenient to choose the space-time path by placing the particle source at a distance very large relative to the dimensions of
M, while the generic point is located at
z along the
z direction and
. Equations (
45)–(47) simplify to
where
. By defining the deflection angle as
one finds
which, in the limit
, yields the Einsteinian result
The index of refraction can be derived from the known equation
. By choosing the direction of propagation of the particle along the
axis, and using (
42), one finds
and, again, for
, or for vanishing
m,
In the case of the metric (
43), one gets the result
3. The Gravitational WKB Problem
We now study the propagation of a scalar field in a gravitational background. We know, from standard quantum mechanics [
14], that
S of (
25) develops an imaginary part when the particle tunnels through a potential. This imaginary contribution is interpreted as the transition amplitude across the classically forbidden region, which is therefore given by [
15]
To
, (
58) becomes
for a space-time path traversing the gravitational background from
to
and back as it must in order to make (
59) invariant. Assuming a Boltzmann distribution for the particles
, where
T is the temperature, we find, in general coordinates,
The intended application here is to the propagation problem in Rindler space given by
with a horizon at
, where
is the constant proper acceleration measured in the rest frame of the Rindler observer. We note that, a priori, our approach is ill-suited to treat this problem which is frequently tackled in the literature starting from exact or highly symmetric solutions of the KG equation [
16]. In fact, the weak field approximation
may become inadequate close to the horizon, from where the imaginary part of
comes, for some systems of coordinates. This requires attention, as discussed below. Nonetheless, the approximation has interesting features, such as the presence of
in (
60) and manifest covariance and invariance under canonical transformations.
It is convenient, for our purposes, to use the Schwarzschild-like form for (
61) using the transformation [
17]
for
and the same transformation with the hyperbolic functions interchanged for
. The resulting metric is
for which the horizon is at
. From (
63) we find
. If
and
represent corrections to the Minkowski metric, we must have
for any
. The approximation therefore remains valid for
. This is sufficient for our calculation. We now write the terms
A and
B, defined in (
25), for the metric (
63) explicitly. We find
and, by taking the reference point
,
The explicit expressions for
A and
B confirm the fact that
receives contributions from both time and space parts of
S, as pointed out in [
17]. On the other hand, this is expected of a fully covariant approach.
The first integrals in
A and
B cancel each other. The second integral in
A can be calculated by contour integration by writing
. The result
yields a vanishing contribution because
reverses its sign on the return trip. The last integral in
B is real. The term
in (
25) contributes the amount
because for a round trip the horizon is crossed twice and each time
because of (
62). The remaining term of (
60) gives
. The final result is therefore
which is independent of
and coincides with the usual Unruh temperature [
18,
19]. This result, with the replacement
, where
is the maximal acceleration, also confirms a recent calculation [
20] regarding particles whose accelerations has an upper limit. Equation (
66) comes in fact from the term
that does not contain derivatives of
. The difference from [
20] and from [
17], is, however, represented by the form of (
59) of the decay rate [
15], which carries a factor 2 in the exponential, as required by our invariant approach.
Despite its limitations, the approximation already reproduces (
66) at
. Additional terms of (
58) are expected to contain corrections to (
66). We note, however, that for a closed space-time path the last integral in (
59) and (
60) becomes
, where
is the surface bounded by the path [
3], and has an imaginary part if
has singularities. This eventuality may call for a complete quantum theory of gravity [
21].
4. “Gravitomagnetic” and “Gravitoelectric” Charges. in Interaction
i. Charge densities. From (
20) and (
6) we obtain
on account of (
4). There are therefore no “magnetic charges” in this version of GEM.
From (
18), the definition of
in (
23) and the Einstein equations
, we find
, which, integrated over all space, is the work done by the field to displace the particle by
in a time
. The charge density is
and
as expected.
ii. Poynting vector. The question we now ask is whether GEM plays a role in radiation problems. Using
, we can construct, for instance, a “Poynting” vector. Assuming, for simplicity, that
in (
19), using known vector identities, by integrating over a finite volume we obtain from (
19) and (
20) the conservation equation
where
is the surface bounding
V and
is the gravitational Poynting vector. Both sides of (
67) acquire, in fact, the dimensions of an energy flux after multiplication by
. We can now calculate the flux of
at the particle assuming that the momentum of the free particle is
and that the source in
V emits a plane gravitational wave in the
x-direction. In this case the wave is determined by the components
and
, and we find
,
,
,
,
and
. It also follows that
and
. The action of
on the quantum particle is directed along the axis of propagation of the wave and results in a combination of oscillations and rotations about the point
with angular momentum given by
,
and
. A similar motion also occurs in the case of Zitterbewegung [
22]. Reverting to normal units, the energy flux associated with this process is
and increases rapidly with the wave frequency
and the particle’s angular momentum.
iii. Electromagnetic radiation. Let us assume that a spinless particle has a charge
q. Acceleration, whatever its cause, makes the particle radiate electromagnetic waves. The four-momentum radiated away by the particle, while passing through the driving gravitational field
, is given by the formula
which can be easily expressed in terms of the external fields (
6) using the equation of motion of the charge in the accelerating field [
23]. At this level of approximation the particle can distinguish uniform acceleration, which gives
, where
g is a constant, from a non-local gravitational field, and it radiates accordingly. This is explained by the presence of
in (
6) and is a direct consequence of our use of the equation of geodesic deviation in (
69).
When the accelerating field is the wave discussed above, the incoming gravitational wave and the emitted electromagnetic wave have the same frequency and the efficiency of the gravity induced production of photons increases as .
iv. Flux quantization. Flux quantization is the typical manifestation of processes in which the wave function is non-integrable. Of interest is here the presence of the free particle momentum in .
Let us consider for simplicity the case of a rotating superfluid. Then
,
and the remaining metric components vanish. The angular velocity
is assumed to be constant in time and
. Without loss of generality, we can also choose the reference point
. We find
and
By integrating over a loop of superfluid, the condition that the superfluid wave function be single-valued gives the quantization condition
where
n is an integer,
and
. The time integrating factor
, extended to
N loops, becomes
, where
and
. The superfluid quantum of circulation satisfies the condition
If the superfluid is charged, then the wave function is single-valued if the total phase satisfies the relation
which, for
and zero external magnetic field, leads to
. In this case, therefore, rotation generates a magnetic flux through
and, obviously, a current in the
N superconducting loops. No fundamental difference is noticed from DeWitt’s original treatment of the problem [
24,
25,
26,
27].
5. Vortices
The vector
is non-vanishing only on surfaces
that satisfy (
19) and (
20) and represent the vortical structures generated by
. At a point
along the path
and
There may then be closed paths embracing the singularities along which the particle wave function must be made single-valued by means of appropriate quantization conditions [
28]. It also follows from (
75) that
is a vortex along which the scalar particles are dragged with acceleration
and relative acceleration
in agreement with the equation of geodesic deviation [
28]. Notice that in (
76) the vorticity is entirely due to
and that
when the motion is irrotational. This also applies when
, in which case the vortices do not develop. Similarly, vortices do not form if
. Each gravitational field produces a distinct vortex whose equations are (
19) and (
20); the vortex dynamics are given by (
76) and (
77); and the topology of the object is supplied by
. Though we started from a quantum wave equation, the vortices generated are purely classical because
and
are classical and the particles interact with gravity as classical particles do. In addition,
and
coexist with the vortices generated by
in the ground state. The field
emerges as a property of gravitation when this interacts with particles described by quantum wave equations. Its range is that of
.
vanishes on the line
along which
can also be eliminated by a gauge transformation. In this case we can say that the line is entirely occupied by
. Obviously
on the nodal lines of
where it loses its meaning. Notice that the right hand side of (
16) can also be replaced by its dual. This is equivalent to interchanging the “magnetic” with the “electric” components of
and the corresponding vortex types.
We finally stress that it is the transformation (
12) that induces the macroscopic phenomena governed by the classical Equations (
19) and (
20). The same transformation thus provides a mechanism by which a classical theory of gravity can be connected with quantum theory.
6. A Minimal Lagrangian
The coordinate x that refers to the total displacement along the path in the local coordinate system has no role in what follows and can be dispensed with.
The simplest possible Lagrangian in which the features discussed in the previous sections can be accommodated is [
29]
where
. The second term of
contains the first order gravitational interaction
met above. By varying
with respect to
and by applying a gauge transformation to
, we find, to
,
and
has now been changed into
because the Goldstone boson has disappeared; the remaining boson is real and so must be its mass [
29]. Equation (
79) is identical to (
9) and its solution is still represented by the boson transformation (
12). However, a variation of
with respect to
now gives
from which, on using (
12) and a gauge transformation, we obtain the field equation
that shows that
has acquired a mass. By expanding
, we find that the mass of
is
v and its range
. Any metrical theory of gravity selected remains valid at distances greater than
, but not so near or below
. The screening current in (
81) determines a situation analogous to that of vortices of normal electrons inside type-II superconductors where the electron normal phase is surrounded by the condensed, superconducting phase. The fundamental difference from the approach followed in the first two sections is represented by (
81) that now becomes a constraint on
. It can be satisfied by requiring that
. No other changes are necessary. On the other hand this condition can be applied directly in
Section 1 and
Section 2 without making use of
.
again vanishes when
, which indicates that the line
can only be occupied by the normal phase. As before, the field
is classical and emerges as a property of gravitation when it interacts with quantum matter. The range of interaction can obviously be very short if
v is large.
7. The One-Dimensional Model
A lattice gas model can be used to calculate the alignment per particle and correlation length that follow from gravity induced condensation. The properties of a many-particle system satisfying (
12) follow from
which strongly resembles the energy function of the Ising model. A difference is represented here by the vectors
(or
) that replace the Ising spin variables
, which are numbers that can take the values
. It is, however, known that a lattice gas model [
30], equivalent to the Ising model, can be set up in which the particles are restricted to lie only on the
N sites of a fine lattice, instead of being allowed to occupy any position in space-time. Then one can associate with each site
i a variable
which takes the value 1 if the site is occupied by a vector
and the value 0 if it is empty. Any distribution of the particles can be indicated by the set of their site occupation numbers
. By replacing
in
H with their average
over the angles in Minkowski space and restricting the interaction to couples of nearest sites, one obtains
where
. By imposing periodic conditions
along the hypercylinder with axis parallel to the time-axis, the partition function becomes
where
and
contains the gravitational contribution due to
. This one-dimensional Ising model can be solved exactly [
30]. Equation (
83) can be rewritten as
and the eigenvalues of
are
and
. As
,
makes a larger contribution than
,
and the Helmholtz free energy per site is
. The alignment per particle for large values of
N is
which yields the gravitational correction contained in
. It also follows from (
84) that there is no spontaneous momentum alignment (
when
) and that complete alignment
is possible only for
. In fact
in the limit
for completely aligned momenta and one can say that there is a phase transition at
, but none for
. It follows from (
84) that the value of
depends on the gravitational contribution
. It also follows that there is no alignment (
) for
(for any
and
m), or for
(no gravity and any
T). According to (
84), complete alignment
can be achieved only at
, which, as shown below, is not, however, a critical temperature in the model.
The correlation length per unit of lattice spacing is
which gives
at
and
at
where thermal agitation can effectively disjoin neighboring sites.
One can also define a gravitational susceptibility as
. One finds
always. It follows that when
,
, and
which is reminiscent of Curie’s law.
Interesting aspects of the problem are revealed by calculating the value of
T for which
has an extremum. The derivative of
with respect to
T vanishes when
which gives
. The temperature at the extremum is
and the corresponding value of the susceptibility is
which is independent of
m. All materials therefore respond to changes in gravity in a universal way that depends only on the source, rather than on the material itself.
Table 1 lists the values of
for some relevant astrophysical objects. In
, the nucleon mass
GeV has been used for simplicity. In general, even a small value of
is sufficient to saturate the alignment of momenta over a range of temperatures, which is narrow because of the sharpness of
. At
, the correlation length is only
which is rather small. This is expected because the values
and
correspond respectively to states of low and high thermal agitation in which the system changes from a high to a small correlation. It is therefore necessary to consider the value of
at a particular temperature.
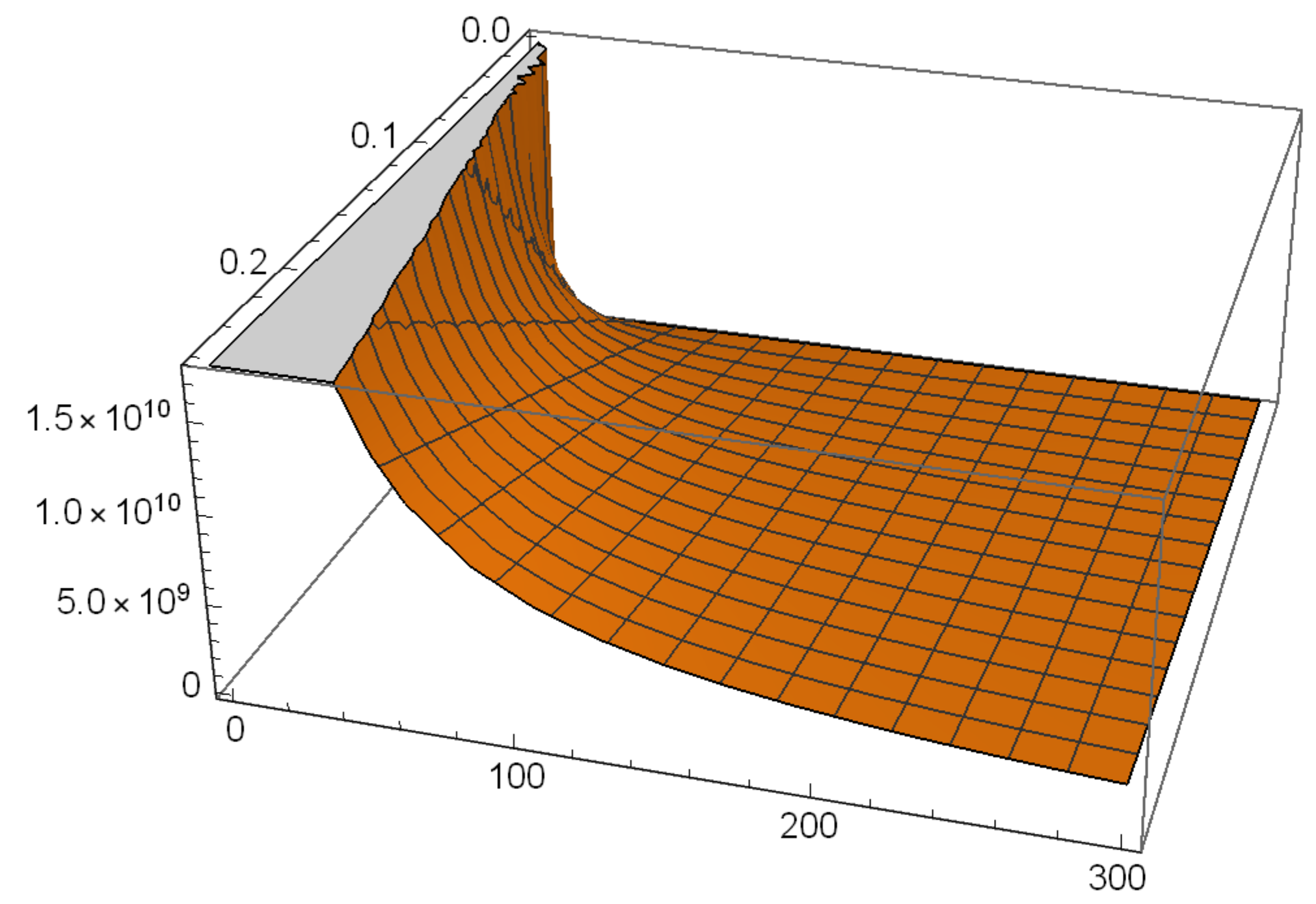
In all cases where , one finds and . This is the high T case. If , then and . For Earth, K yields and .
It follows from
Table 1 and from
Figure 1 and
Figure 2, that condensation effects can be large even though
is small, provided
retains a reasonable value. This is an unusual occurrence in gravitation. The effect should be observable by comparing
at
for different materials.
The oscillations of
are similar to spin waves and obey the dispersion relation [
28,
31]
where
s is the spin magnitude at a site,
is the spin-wave momentum and
a is the lattice spacing. Upon quantization, spin waves give rise to quasiparticles that, by analogy with magnons, shall be called “gravons”. For oscillations of small amplitude and on using (
90), one obtains
, where
is taken as the gravon’s effective mass. If the lattice subdivision is very fine so that
, then
can become large for small
and the oscillation frequency of these waves is very low. Magnons can, of course, be created in laboratory experiments by scattering neutrons against an ordered magnetic structure. The analogous gravon experiment in Earth or near space laboratories, seems to be precluded by the high values of
for small
. It would be useful, for astrophysical purposes, to derive a gravon’s spectrum and distribution. For sufficiently small changes of
, the energy of a mode of energy
and
gravons is that of a harmonic oscillator and the gravon distribution is that of Planck. When
, the number of gravons per unit volume is
also reminiscent of Bloch
law for magnetism. As indicated by
Figure 2, the approach to the Curie point is less sharp than in magnetism. This is due to the mitigating action that a small
has on
in
as
. Curie’s law and (
91) suggest
as a critical temperature. It is shown in the next section that this choice is, however, inappropriate.
Finally, the radiation spectrum of gravons produced by a proton a distance
b from a star of mass
M can be calculated from the power radiated in the process of
using the expression
where
and
represents the gravon. The process is similar to that of magnon production by neutron scattering by a magnetic structure. The quantum mechanical power spectrum of
is
where
is the momentum of the incoming nucleon and
to satisfy the requirement
, where
is the emission angle. Results (
90) and (
94) agree for
.
If
, the total number of gravons can be written in the form
where
and
is the typical size of the system. From
, one gets
which can be satisfied for sufficiently large
L.
8. A Two-Dimensional Model
Not all ordered phases can exist, because the number of space dimensions plays a role in phase changes. Changes to ordered phases can survive only if they are stable against long wavelength fluctuations. Consider, for instance, a system of particles that is invariant under translations in a space V of d dimensions. Representing the deviation of the particles from the equilibrium position by , where i indicates the normal modes and k extends up to some value, the normal modes energy is by the theorem of equipartition of energy. Then for , . If the continuous symmetry has been broken spontaneously, the excitations whose frequencies , vanish as and give the low frequency limit <q> which diverges for . Hence the lowest critical dimension is , below which order is destroyed by long wavelength fluctuations.
Consider, therefore, the case
d = 2. The quickest way to obtain the relevant expressions for a two-dimensional model is to restart from (
82) and replace the vectors
with classical vectors constrained to lie in the
–plane. Then
and
and
if
i and
j are neighbors;
otherwise. If the neighboring angles are close in value, then by neglecting an irrelevant constant,
, where
is the nearest neighbor of
. When replacing the finite differences with derivatives one gets
These excitations are vortices for which
and
n is an integer. The energy of an isolated vortex is
, where
L is the linear dimension of the vortex. The entropy associated with a single vortex is
and the change in free energy due to the formation of a vortex is
which is positive for
Isolated vortices do not therefore form for . At low temperatures the state of the system consists of an equilibrium density of bound vortices. At the vortices become unbound and the condensed phase is destroyed.
The condition
gives in two dimensions
which can be satisfied for
provided
.
Given the important role of space dimensionality in critical phenomena, one may wonder about the behavior of in dimensions higher than two. In three dimensions the condition can be satisfied at all T for sufficiently high values of .
9. Summary and Conclusions
A rotationally-invariant quantum system acquires a privileged direction in the course of its evolution in curved space-time. This symmetry breaking takes the form of a space-time-dependent ground state (
12) and of a topological singularity in (
13) that leads to the phenomenon of condensation in an ensemble of like particles. In the re-distribution of degrees of freedom that follows symmetry breaking, the gravitational field is represented by the two-point potential
. The tensor
satisfies Maxwell-type equations and depends on the metric tensor. The potential
suggests the introduction of the notion of the quasiparticle, because gravity affects, in general, the dispersion relations of the particles with which it interacts, as shown by (
29), and because it carries with itself information about matter through
.
A simple Lagrangian was introduced to illustrate how acquires a mass v and a range . Above the gravitational interaction is conveyed by , but below this range, when interacting with matter, the gravitational action is carried by . The screening current associated with a massive resembles what occurs with vortices of normal electrons in type-II superconductors where the electron normal phase is surrounded by the condensed superconducting phase. The normal phase remains shielded from the external gravitational field, a situation that is of interest in dark matter studies. The field is classical and emerges as a property of gravitation when the latter interacts with quantum matter.
Some applications of GEM have been examined in some detail.
The equations obeyed by
do not contemplate the presence of “gravitomagnetic” charges. This follows immediately from (
20) and (
4).
The “gravitoelectric” charge density follows from when , and after integration over space, can be interpreted as the amount of work done by the gravitational field to deflect the particle by an amount in a time .
Some particular aspects of the behavior of have been examined. We have found that when , scale invariance assures that a gas of gravitons satisfies Planck’s radiation law, but that this is no longer so, in principle, for non-pure gravitational fields.
also determines the equations of motion of a particle through (
30)–(
32) and (
21). We have found that the motion follows a geodesic only if the quantum particle chooses, among all available paths, that for which
. Along this particular path the principle of equivalence is satisfied. We have then shown that the particle motion is contained in the solution (
12) of the covariant KG equation.
We have also studied quantum mechanical tunneling through a horizon and derived a covariant and canonical invariant expression for the transition amplitude. Though the approximation looks ill-suited to deal with regions of space-time close to a gravitational horizon, the approximation reproduces the Unruh temperature exactly in the case of the Rindler metric. No corrections of and no effects due to
have been found for the standard result of
. Higher order approximations can be calculated by applying (
60).
As
satisfies Maxwell-like equations, it is also possible to define a Poynting vector and a flux of energy and angular momentum at the particle so that the particle’s motion can be understood as a sequence of oscillations and rotations similar to what is found in the case of Zitterbewegung [
22].
Use of
in problems where gravity accelerates a charged particle and electromagnetic radiation is produced offers a rather immediate relationship between the loss of energy-momentum by the quantum particle and the driving gravitational field. These processes could give sizable contributions for extremely high values of
. Astrophysical processes like photoproduction [
32] and synchrotron radiation [
33] have been discussed in the literature and are worthy of re-consideration in view of the present results. An advantage from the point of view of detecting high frequency gravitational radiation, for which detection schemes are in general difficult to conceive, is represented by the efficiency of the graviton–photon conversion rate and by the high coupling afforded by a radio receiver over, for instance, a mechanical one. This would enable, in principle, a spectroscopic analysis of the signal.
In the last problem considered, we have calculated the flux of
in the typical quantum case of a non-integrable wave function. Here too, it is possible to isolate quantities of physical interest, such as magnetic flux or circulation, despite the non-intuitive character of
. Unlike [
24], our procedure and results are fully relativistic. They can be applied directly to boson condensates in boson stars [
34].
Covariant wave equations have solutions (
12) and (
21) that are space-time-dependent transformations of the vacuum. The resulting degeneracy of the ground states produces Nambu-Goldstone excitations which break the rotational symmetry of the system. The quasiparticles generated, or gravons, are oscillations that obey the dispersion relation (
90) and have an effective mass.
In the one-dimensional Ising model considered, the order parameter is the generalized momentum
, along which the particle momenta tend to align. The motion of the particles in the direction of
is along geodesics. Off them, along the variable
z,
is topologically singular and length scales change. The phase singularities of
give rise to quantized vortices [
35], and the particle motion along the hypersurfaces
satisfies the equation of deviation. Phase singularities give rise to strings of silence in acoustics; lines of magnetic flux in magnetism; and vortices in optics, in superfluids and superconductors [
35]. The multivalued nature of
leads to the loss of a standard of length in the region of critical phenomena. For space-time loops linking the regions of singularity, one must have
where
is a surface bound by
. Outside the critical region the change in length still vanishes around paths
that do not link any singularity. The field
vanishes on the line
which is entirely occupied by the normal phase. In addition, the choice
in (
18), would give a Meissner-type effect for
. The result is here analogous to that of superconducting strings. It is also remarkable that a singularity in a quantum mechanical wave function produces a field
that is entirely classical.
The effect of gravity on some parameters that characterize the critical behavior of a quantum system of scalar particles can be calculated. For instance, the gravitational susceptibility
is always positive and obeys a Curie-type law. The susceptibility can be understood as a measure of the reaction of the system to a gravitational field and is analogous to the magnetic susceptibility. There are, of course, no gravitational dipoles in an ensemble of quantum particles because Einstein’s gravity is always attractive. There are only the particle momentum vectors in the lattice gas model considered. Therefore,
indicates only how the momentum alignment per particle changes when the gravitational parameter
changes. Since
always satisfies (
86), the response to changes in
can be termed “paragravitational”. The increase is larger as
because at lower temperatures thermal agitation subsides and correlation is preserved.
The number of quantized spin-waves, or gravons, per unit volume, follows a law; the emission cross-section is low; and the gravon spectrum depends linearly on the momentum ℓ, both classically and quantum mechanically, if .
In the one-dimensional case one cannot say that
is the critical temperature of the model. The lowest critical dimension is 2 and the simplest two-dimensional system is the
-model. A critical temperature is in fact given by (
99), below which isolated vortices do not exist; only bound vortices do. Symmetry breaking has a topological origin also in the
-model. Due to the important developments that have recently taken place in the field of condensed matter physics, such as block spin models and renormalization, the prospects of extending the results to dimensions greater than one look promising and are under consideration.
Summarizing, the solution (
12) and its extension (
21) introduce topological singularities and induce condensation. This gives rise to the classical and quantum aspects of GEM discussed above when gravity interacts with quantum matter.