A New Validity Index Based on Fuzzy Energy and Fuzzy Entropy Measures in Fuzzy Clustering Problems
Abstract
:1. Introduction
2. Preliminaries
2.1. Fuzzy Energy and Entropy Measures
- (1)
- e(0) = 0
- (2)
- e(1) = 1
- (3)
- e is monotonically increasing.
- (4)
- h(1) = 0
- (5)
- h(u) = h(1 − u)
- (6)
- h is monotonically increasing in [0, ½]
- (7)
- h is monotonically decreasing in [½, 1].
2.2. Fuzzy C-Means Algorithm
| Algorithm 1:FCM |
| Input: Dataset X = {x1, …, xN} Output: Cluster centers V = {v1, …, vC}; Partition matrix U Arguments: number of clusters C; fuzzifier p; stop iteration threshold ε
|
3. The Proposed FCM Algorithm Based on a Fuzzy Energy and Entropy Validity Index
| Algorithm 2:PEHFCM. |
| Input: Dataset X = {x1, …, xN} Output: Cluster centers V = {v1, …, vC}; Partition matrix U, optimal number of clusters C* Arguments: max num of clusters, Cmax; max num of random selections of the initial cluster centers, Smax, fuzzifier p; stop iteration threshold ε
|
| Algorithm 3:FCMV |
| Input: Dataset X = {x1, …, xN} Initial cluster centers V0 = {v10, …, vC0} Output: Cluster centers V = {v1, …, vC}; Partition matrix U Arguments: Initial cluster centers V0 = {v10, …, vC0}; number of clusters C; fuzzifier p; stop iteration threshold ε
|
4. Results
- -
- The mean percent of gain (or loss) of running time. If TC is a running time calculated by running a FCM-based method and TCPEH is the one calculated with PEHFCM, this index is given by the average of the percentage of (TCPEH − TC)/TCPEH. This value is equal to 0 for PEHFCM.
- -
- The mean percentage gain (or loss) of a classification index. If IC is a classification index value obtained by running a FCM-based method and ICPEH is the one obtained with PEHFCM, this index is given by the average of the percentage of (IC − ICPEH)/ICPEH. This value is equal to 0 for PEHFCM.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bezdek, J.C. Pattern Recognition with Fuzzy Objective Function Algorithms; Kluwer Academic Publishers: Norwell, MA, USA, 1981. [Google Scholar]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Chen, J.; Qin, Z.; Jia, J. A Weighted Mean Subtractive Clustering Algorithm. Inf. Technol. J. 2008, 7, 356–360. [Google Scholar] [CrossRef] [Green Version]
- Yang, Q.; Zhang, D.; Tian, F. A initialization method for Fuzzy C-means algorithm using Subtractive Clustering. In Proceedings of the Third International Conference on Intelligent Networks and Intelligent Systems, Shenyang, China, 1–3 November 2010; Volume 10, pp. 393–396. [Google Scholar]
- Campello, R.J.G.B.; Hruschka, E.R. A fuzzy extension of the silhouette width criterion for cluster analysis. Fuzzy Sets Syst. 2006, 157, 2858–2875. [Google Scholar] [CrossRef]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis, 5th ed.; Arnold: Paris, France, 2011; p. 343. ISBN 978-0-470-74991-3. [Google Scholar]
- Gath, I.; Geva, A.B. Unsupervised optimal fuzzy clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 773–781. [Google Scholar] [CrossRef]
- Xie, X.L.; Beni, I.G. A validity measure for fuzzy clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 841–847. [Google Scholar] [CrossRef]
- Zou, K.-Q.; Wang, Z.-P.; Pei, S.-J.; Hu, M. A New Initialization Method for Fuzzy c-Means Algorithm Based on Density. In Advances in Multimedia, Software Engineering and Computing Vol.2; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2009; Volume 54, pp. 547–553. [Google Scholar]
- Hayet, D.; Hamza, C.; Mostefa, B.; Nadjette, D.H. Initialization Methods for K-means and Fuzzy Cmeans Clustering Algorithm. In Proceedings of the International Conference on Automatic, Télécommunication, and Signals, Annaba, Algeria, 16–18 November 2015. [Google Scholar] [CrossRef]
- Trauvert, E. On the meaning of Dunn’s partition coefficient for fuzzy clusters. Fuzzy Sets Syst. 1988, 25, 217–242. [Google Scholar] [CrossRef]
- Bezdek, J.C. Cluster validity with fuzzy sets. J. Cybern. 1973, 3, 58–73. [Google Scholar] [CrossRef]
- Ding, Y.; Fu, X. Kernel-based fuzzy c-means clustering algorithm based on genetic algorithm. Neurocomputing 2016, 188, 233–238. [Google Scholar] [CrossRef]
- Li, D.; Han, Z.; Zhao, J. A Novel Level Set Method with Improved Fuzzy C-Means Based on Genetic Algorithm for Image Segmentation. In Proceedings of the 2017 3rd International Conference on Big Data Computing and Communications (BIGCOM), Chengdu, China, 10–11 August 2017; pp. 151–157. [Google Scholar]
- Siringoringo, R.; Jamaluddin, J. Initializing the Fuzzy C-Means Cluster Center with Particle Swarm Optimization for Sentiment Clustering. In Proceedings 1st International Conference of SNIKOM 2018; IOP Publishing: Bristol, UK, 2019; Volume 1361, p. 012002. [Google Scholar]
- Franco, D.G.D.B.; Steiner, M.T.A. Clustering of solar energy facilities using a hybrid fuzzy c-means algorithm initialized by metaheuristics. J. Clean. Prod. 2018, 191, 445–457. [Google Scholar] [CrossRef]
- De Luca, A.; Termini, S. Entropy and energy measures of fuzzy sets. In Advances in Fuzzy Set Theory and Applications; Gupta, M.M., Ragade, R.K., Yager, R.R., Eds.; North-Holland: Amsterdam, The Netherlands, 1979; pp. 321–338. [Google Scholar]
- De Luca, A.; Termini, S. A definition of non-probabilistic entropy in the setting of fuzzy sets theory. Inf. Control 1972, 20, 301–312. [Google Scholar] [CrossRef] [Green Version]
- Cardone, B.; Di Martino, F. A Novel Fuzzy Entropy-Based Method to Improve the Performance of the Fuzzy C-Means Algorithm. Electronics 2020, 9, 554. [Google Scholar] [CrossRef] [Green Version]
- Fukuyama, Y.; Sugeno, M. A new method of choosing the number of clusters for the fuzzy C-means method. In Proceedings of the Fifth Fuzzy Systems Symposium, Kobe, Japan, 2–3 June 1989; pp. 247–250. [Google Scholar]
- Wu, K.L.; Yang, M.S. A fuzzy validity index for fuzzy clustering. Pattern Recognit. Lett. 2005, 26, 1275–1291. [Google Scholar] [CrossRef]
- Ming, T.K. Encyclopedia of Machine Learning; Sammut, C., Webb, G.I., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; ISBN 978-0-387-30164-8. [Google Scholar]
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2018, 13. [Google Scholar] [CrossRef]
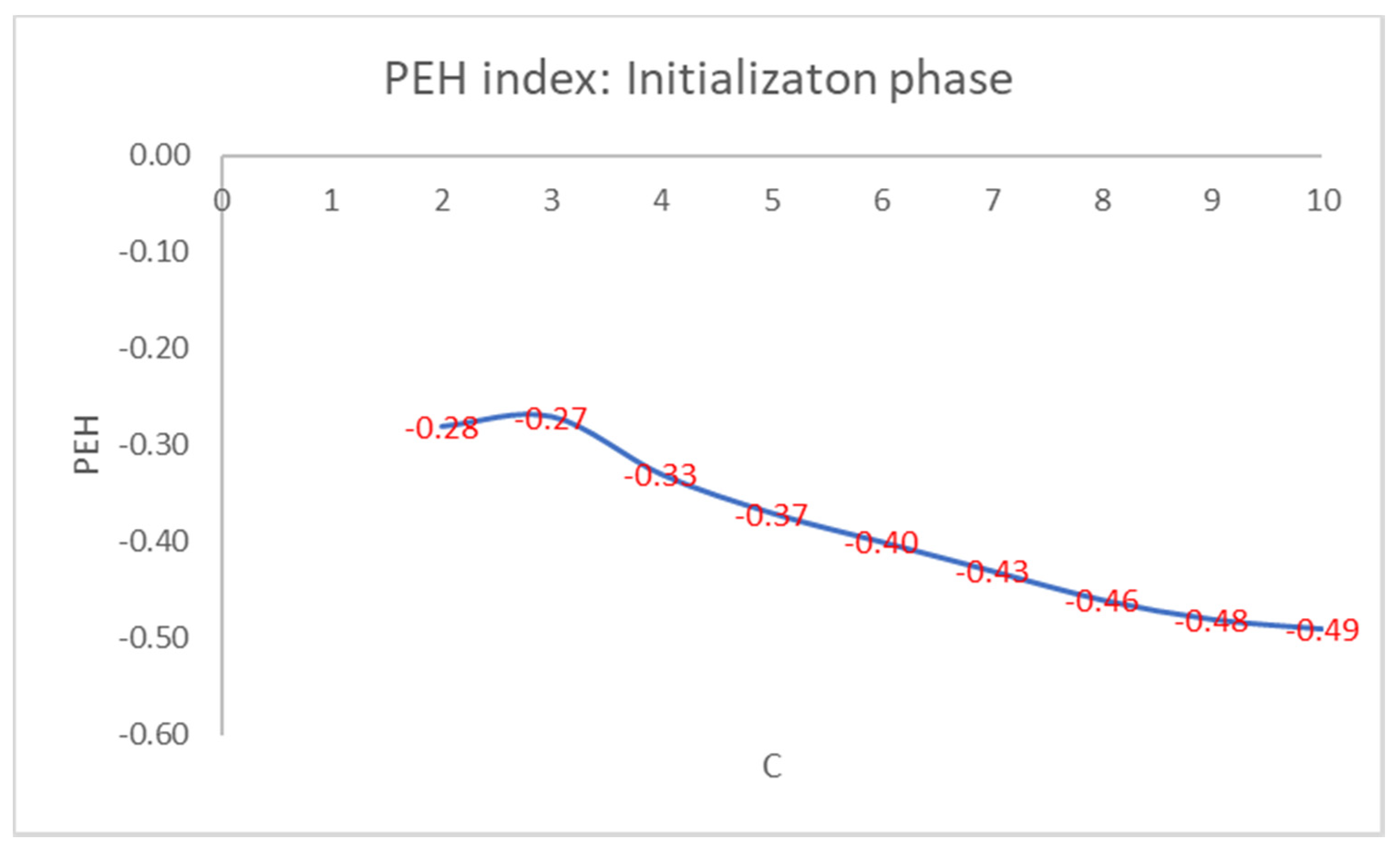



| Method | Number of Clusters | Iterations | Running Time (s) |
|---|---|---|---|
| FCM + PC | 2 | 15 | 0.158 |
| FCM + PE | 2 | 15 | 0.157 |
| FCM + FS | 3 | 13 | 0.138 |
| FCM + XB | 3 | 13 | 0.135 |
| FCM + PCAES | 3 | 13 | 0.133 |
| PEHFCM | 3 | 11 | 0.103 |
| Index | FCM + FS | FCM + XB | FCM + PCAES | PEHFCM | EwFCM | PSOFCM |
|---|---|---|---|---|---|---|
| Running time (s) | 0.138 | 0.135 | 0.139 | 0.103 | 0.112 | 0.134 |
| Accuracy | 94.22% | 94.67% | 94.67% | 96.00% | 96.44% | 96.44% |
| Precision | 91.33% | 92.00% | 92.22% | 94.00% | 94.67% | 94.67% |
| Recall | 91.34% | 92.00% | 92.21% | 94.01% | 94.66% | 94.67% |
| F1 Score | 91.33% | 92.00% | 92.21% | 94.00% | 94.66% | 94.67% |
| Method | Number of Clusters | Iterations | Running Time (s) |
|---|---|---|---|
| FCM + PC | 2 | 17 | 0.166 |
| FCM + PE | 2 | 17 | 0.168 |
| FCM + FS | 3 | 16 | 0.152 |
| FCM + XB | 3 | 16 | 0.151 |
| FCM + PCAES | 3 | 16 | 0.146 |
| PEHFCM | 3 | 12 | 0.116 |
| Index | FCM + FS | FCM + XB | FCM + PCAES | PEHFCM | EwFCM | PSOFCM |
|---|---|---|---|---|---|---|
| Running time (s) | 0.152 | 0.151 | 0.154 | 0.116 | 0.137 | 0.145 |
| Accuracy | 90.16% | 90.34% | 90.45% | 92.91% | 93.50% | 93.81% |
| Precision | 85.89% | 86.03% | 86.06% | 88.67% | 90.04% | 90.61% |
| Recall | 86.09% | 86.18% | 86.21% | 88.61% | 90.48% | 90.84% |
| F1 Score | 85.99% | 86.10% | 86.13% | 88.64% | 90.26% | 90.72% |
| Dataset | Features | Data Points | Parameter | FCM + FS | FCM + XB | FCM + PCAES | PEHFCM | EwFCM | PSOFCM |
|---|---|---|---|---|---|---|---|---|---|
| Breast cancer | 32 | 569 | Number of clusters Accuracy | 2 | 2 | 2 | 2 | 2 | 2 |
| 84.41% | 84.29% | 84.37 | 94.75% | 95.32% | 95.68% | ||||
| Glass | 9 | 214 | Number of clusters Accuracy | 6 | 6 | 6 | 6 | 6 | 6 |
| 88.70% | 88.72% | 88.78% | 89.68% | 89.45% | 89.70% | ||||
| Iris | 4 | 150 | Number of clusters Accuracy | 3 | 3 | 3 | 3 | 3 | 3 |
| 94.22% | 94.67% | 94.67% | 96.00% | 96.44% | 96.44% | ||||
| Seeds | 7 | 210 | Number of clusters Accuracy | 3 | 3 | 3 | 3 | 3 | 3 |
| 89.48% | 89.42% | 89.55% | 90.64% | 90.75% | 90.81% | ||||
| Sonar | 60 | 208 | Number of clusters Accuracy | 2 | 2 | 2 | 2 | 2 | 2 |
| 72.18% | 72.27% | 72.27% | 78.41% | 78.83% | 78.76% | ||||
| Vehicle | 19 | 846 | Number of clusters Accuracy | 4 | 4 | 4 | 4 | 4 | 4 |
| 63.21% | 63.10% | 63.15% | 65.64% | 65.90% | 66.08% | ||||
| Wine | 13 | 178 | Number of clusters Accuracy | 3 | 3 | 3 | 3 | 3 | 3 |
| 90.16% | 90.34% | 90.45% | 92.91% | 93.50% | 93.81% |
| Index | FCM + FS | FCM + XB | FCM + PCAES | PEHFCM | EwFCM | PSO FCM |
|---|---|---|---|---|---|---|
| Percentage gain of running time | −39.16% | −39.01% | −38.94% | 0.00% | −28.06% | −31.57% |
| Percentage gain of accuracy | −3.14% | −3.11% | −3.06% | 0.00% | +0.91% | +0.93% |
| Percentage gain of precision | −3.28% | −3.25% | −3.19% | 0.00% | +1.74% | +1.77% |
| Percentage gain of recall | −3.22% | −3.26% | −3.18% | 0.00% | +1.71% | +1.74% |
| Percentage gain of F1 Score | −3.25% | −3.25% | −3.19% | 0.00% | +1.72% | +1.76% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martino, F.D.; Sessa, S. A New Validity Index Based on Fuzzy Energy and Fuzzy Entropy Measures in Fuzzy Clustering Problems. Entropy 2020, 22, 1200. https://doi.org/10.3390/e22111200
Martino FD, Sessa S. A New Validity Index Based on Fuzzy Energy and Fuzzy Entropy Measures in Fuzzy Clustering Problems. Entropy. 2020; 22(11):1200. https://doi.org/10.3390/e22111200
Chicago/Turabian StyleMartino, Ferdinando Di, and Salvatore Sessa. 2020. "A New Validity Index Based on Fuzzy Energy and Fuzzy Entropy Measures in Fuzzy Clustering Problems" Entropy 22, no. 11: 1200. https://doi.org/10.3390/e22111200
APA StyleMartino, F. D., & Sessa, S. (2020). A New Validity Index Based on Fuzzy Energy and Fuzzy Entropy Measures in Fuzzy Clustering Problems. Entropy, 22(11), 1200. https://doi.org/10.3390/e22111200






