Dynamics of Coordinate Ascent Variational Inference: A Case Study in 2D Ising Models
Abstract
1. Introduction
2. Mean-Field Variational Inference and the Coordinate Ascent Algorithm
| Algorithm 1 Coordinate ascent variational inference (CAVI). |
 |
3. CAVI in Ising Model
Mean Field Variational Inference in Ising Model
4. Why the Ising Model: A Summary of Our Contributions
Statistical Significance of Our Results
5. Main Results
5.1. Sigmoid Function Dynamics
- 1.
- For , the system has a single hyperbolic fixed point which is a global attractor and there are no p-periodic points for .
- 2.
- For , the system has one repelling hyperbolic fixed point and two hyperbolic stable fixed points , , with , and stable sets , . There are no p-periodic points for .
- 3.
- For , the system has one unstable hyperbolic fixed point , and a stable 2-cycle with stable set , with . There are no p-periodic points for .
- 4.
- For , the system has one non-hyperbolic fixed point at which is asymptotically stable and attracting.
- 1.
- For , the system has a single hyperbolic fixed point which is a global attractor and there are no p-periodic points for .
- 2.
- For , the system has one repelling hyperbolic fixed point and two hyperbolic stable fixed points , , with , and stable sets , .
- 3.
- For , the system has one non-hyperbolic fixed point at which is asymptotically stable and attracting.
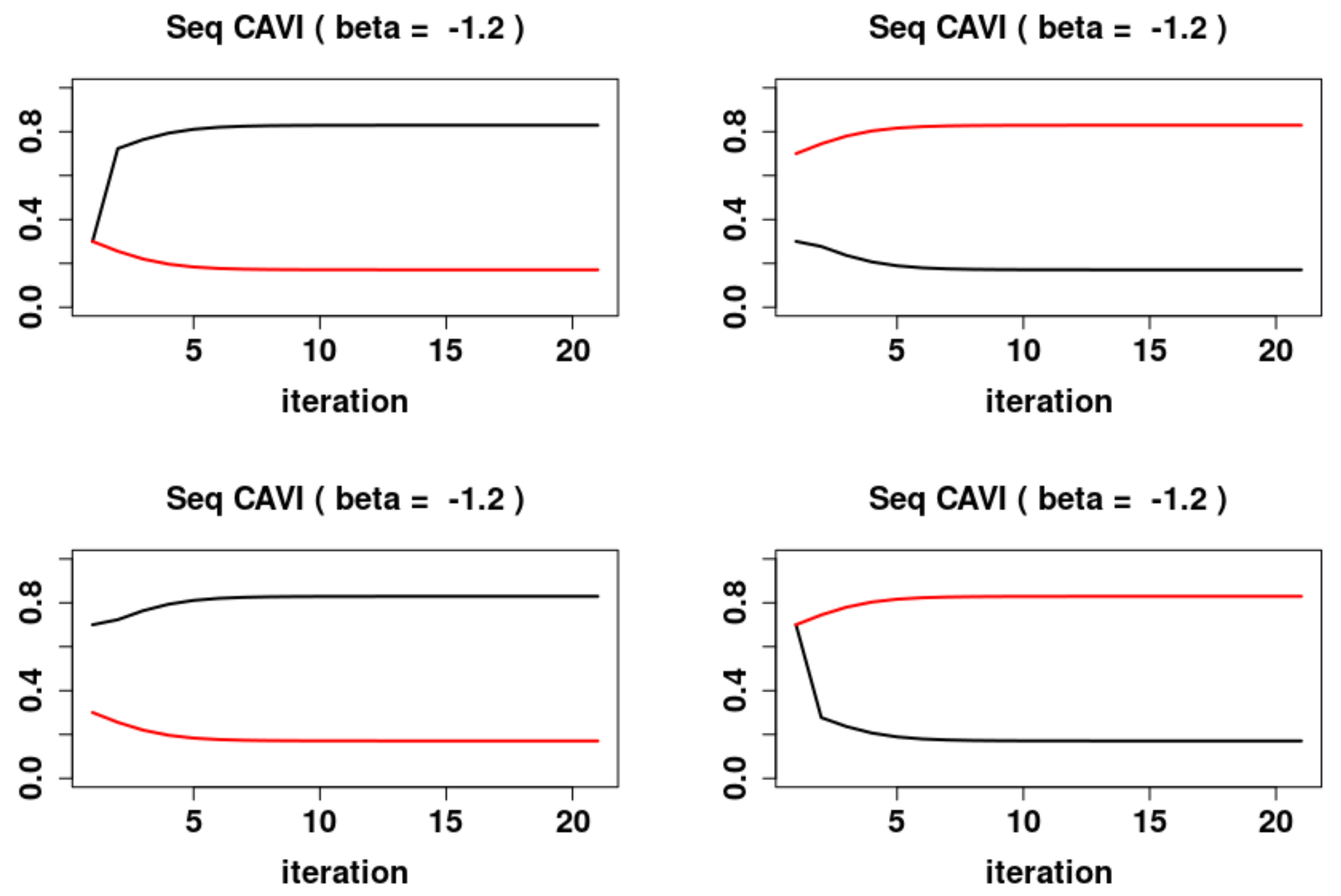
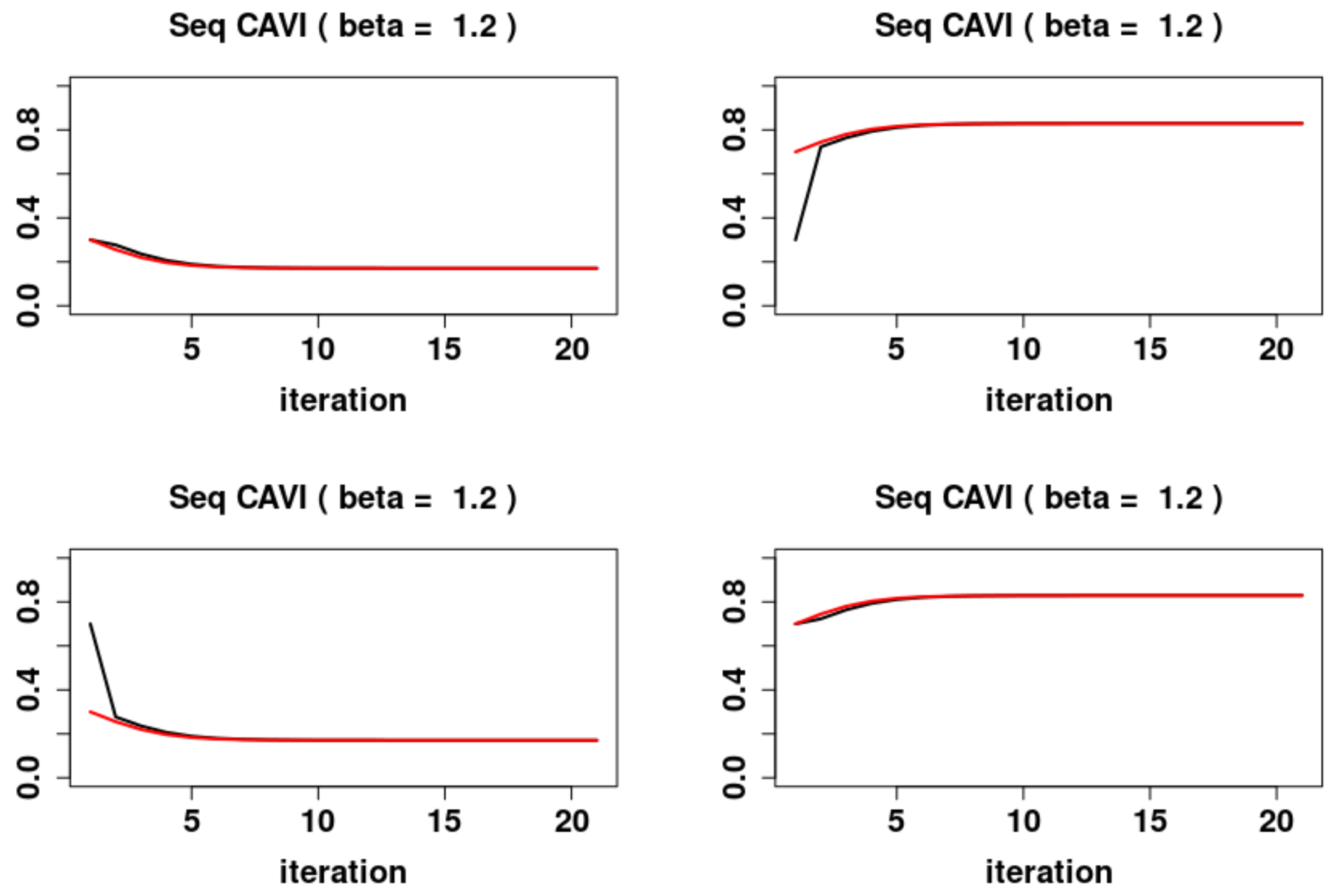
5.2. Sequential Dynamics

- 1.
- For , the system has the system has one locally asymptotically unstable fixed point and two locally asymptotically stable fixed points and , with stable sets and respectively.
- 2.
- For , the system has a global asymptotically stable fixed point .
- 3.
- For the system has the system has one locally asymptotically unstable fixed point and two locally asymptotically stable fixed points and , with domains of attraction and respectively.
5.3. Parallel Updates

- 1.
- For , the system has two locally asymptotically stable fixed points and , and one locally asymptotically unstable fixed point , where and are the fixed points of (11). Furthermore the system exhibits periodic behavior in the form of 2-cycles. The asymptotically stable 2-cycle, and asymptotically unstable 2-cycles,The stable sets are
- 2.
- For , the system has a global attracting fixed point .
- 3.
- For , the system has two locally asymptotically stable fixed points and , and one locally asymptotically unstable fixed point , where and are the fixed points of (11). Furthermore the system exhibits periodic behavior in the form of 2-cycles. The asymptotically stable 2-cycle, and asymptotically unstable 2-cycles, and . The stable sets are
5.4. A Comparison of the Dynamics


6. Edward–Sokal Coupling
6.1. Random Cluster Model
6.2. VI Objective Function
6.3. VI Updates
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. An Overview of One Dimensional Dynamical Systems
Appendix A.1. Notation
Appendix A.2. Dynamical Systems

- 1.
- If then is semi-asymptotically stable from the left if and semi-asymptotically stable from the right if ;
- 2.
- if and then is asymptotically stable;
- 3.
- if and then is unstable.
- 1.
- If , then is asymptotically stable;
- 2.
- If , then is unstable.
Appendix A.3. Codimension 1 Bifurcations
- 1.
- 2.


References
- Bishop, C. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: Berlin/Heidelberger, Germany, 2006. [Google Scholar]
- MacKay, D.J.; Mac Kay, D.J. Information Theory, Inference and Learning Algorithms; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational Inference: A Review for Statisticians. J. Am. Stat. Assoc. 2017, 112, 859–877. [Google Scholar] [CrossRef]
- Zhang, C.; Bütepage, J.; Kjellström, H.; Mandt, S. Advances in variational inference. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2008–2026. [Google Scholar] [CrossRef] [PubMed]
- Parisi, G. Statistical Field Theory; Frontiers in Physics; Addison-Wesley: Boston, MA, USA, 1988. [Google Scholar]
- Opper, M.; Saad, D. Advanced Mean Field Methods: Theory and Practice; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Gabrié, M. Mean-field inference methods for neural networks. J. Phys. A Math. Theor. 2020, 53, 223002. [Google Scholar] [CrossRef]
- Alquier, P.; Ridgway, J.; Chopin, N. On the properties of variational approximations of Gibbs posteriors. J. Mach. Learn. Res. 2016, 17, 1–41. [Google Scholar]
- Pati, D.; Bhattacharya, A.; Yang, Y. On statistical optimality of variational Bayes. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Canary Islands, Spain, 9–11 April 2018; pp. 1579–1588. [Google Scholar]
- Yang, Y.; Pati, D.; Bhattacharya, A. α-Variational inference with statistical guarantees. Ann. Stat. 2020, 48, 886–905. [Google Scholar] [CrossRef]
- Chérief-Abdellatif, B.E.; Alquier, P. Consistency of variational Bayes inference for estimation and model selection in mixtures. Electron. J. Stat. 2018, 12, 2995–3035. [Google Scholar] [CrossRef]
- Wang, Y.; Blei, D.M. Frequentist consistency of variational Bayes. J. Am. Stat. Assoc. 2019, 114, 1147–1161. [Google Scholar] [CrossRef]
- Wang, Y.; Blei, D.M. Variational Bayes under Model Misspecification. arXiv 2019, arXiv:1905.10859. [Google Scholar]
- Wang, B.; Titterington, D. Inadequacy of Interval Estimates Corresponding to Variational Bayesian Approximations; AISTATS; Citeseer: Princeton, NJ, USA, 2005. [Google Scholar]
- Wang, B.; Titterington, D. Convergence properties of a general algorithm for calculating variational Bayesian estimates for a normal mixture model. Bayesian Anal. 2006, 1, 625–650. [Google Scholar] [CrossRef]
- Zhang, A.Y.; Zhou, H.H. Theoretical and Computational Guarantees of Mean Field Variational Inference for Community Detection. arXiv 2017, arXiv:math.ST/1710.11268. [Google Scholar]
- Mukherjee, S.S.; Sarkar, P.; Wang, Y.R.; Yan, B. Mean field for the stochastic blockmodel: Optimization landscape and convergence issues. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2018; pp. 10694–10704. [Google Scholar]
- Sarkar, P.; Wang, Y.; Mukherjee, S.S. When random initializations help: A study of variational inference for community detection. arXiv 2019, arXiv:1905.06661. [Google Scholar]
- Yin, M.; Wang, Y.X.R.; Sarkar, P. A Theoretical Case Study of Structured Variational Inference for Community Detection. Proc. Mach. Learn. Res. 2020, 108, 3750–3761. [Google Scholar]
- Ghorbani, B.; Javadi, H.; Montanari, A. An Instability in Variational Inference for Topic Models. arXiv 2018, arXiv:stat.ML/1802.00568. [Google Scholar]
- Jain, V.; Koehler, F.; Mossel, E. The Mean-Field Approximation: Information Inequalities, Algorithms, and Complexity. arXiv 2018, arXiv:cs.LG/1802.06126. [Google Scholar]
- Koehler, F. Fast Convergence of Belief Propagation to Global Optima: Beyond Correlation Decay. arXiv 2019, arXiv:cs.LG/1905.09992. [Google Scholar]
- Kuznetsov, Y. Elements of Applied Bifurcation Theory; Applied Mathematical Sciences; Springer: New York, NY, USA, 2008. [Google Scholar]
- Kuznetsov, Y.; Meijer, H. Numerical Bifurcation Analysis of Maps; Cambridge Monographs on Applied and Computational Mathematics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Wiggins, S. Introduction to Applied Nonlinear Dynamical Systems and Chaos; Texts in Applied Mathematics; Springer: New York, NY, USA, 2003. [Google Scholar]
- Friedli, S.; Velenik, Y. Statistical Mechanics of Lattice Systems: A Concrete Mathematical Introduction; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Ising, E. Beitrag zur theorie des ferromagnetismus. Zeitschrift für Physik 1925, 31, 253–258. [Google Scholar] [CrossRef]
- Onsager, L. Crystal Statistics. I. A Two-Dimensional Model with an Order-Disorder Transition. Phys. Rev. 1944, 65, 117–149. [Google Scholar] [CrossRef]
- Toda, M.; Toda, M.; Saito, N.; Kubo, R.; Saito, N. Statistical Physics I: Equilibrium Statistical Mechanics; Springer Series in Solid-State Sciences; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Moessner, R.; Ramirez, A.P. Geometrical frustration. Phys. Today 2006, 59, 24. [Google Scholar] [CrossRef]
- Basak, A.; Mukherjee, S. Universality of the mean-field for the Potts model. Probab. Theory Relat. Fields 2017, 168, 557–600. [Google Scholar] [CrossRef]
- Blanca, A.; Chen, Z.; Vigoda, E. Swendsen-Wang dynamics for general graphs in the tree uniqueness region. Random Struct. Algorithms 2019, 56, 373–400. [Google Scholar] [CrossRef]
- Guo, H.; Jerrum, M. Random cluster dynamics for the Ising model is rapidly mixing. Ann. Appl. Probab. 2018, 28, 1292–1313. [Google Scholar] [CrossRef]
- Oostwal, E.; Straat, M.; Biehl, M. Hidden Unit Specialization in Layered Neural Networks: ReLU vs. Sigmoidal Activation. arXiv 2019, arXiv:1910.07476. [Google Scholar]
- Çakmak, B.; Opper, M. A Dynamical Mean-Field Theory for Learning in Restricted Boltzmann Machines. arXiv 2020, arXiv:2005.01560. [Google Scholar] [CrossRef]
- Blum, E.; Wang, X. Stability of fixed points and periodic orbits and bifurcations in analog neural networks. Neural Netw. 1992, 5, 577–587. [Google Scholar] [CrossRef]
- Grimmett, G. The Random-Cluster Model; Grundlehren der Mathematischen Wissenschaften; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Elaydi, S. Discrete Chaos: With Applications in Science and Engineering; CRC Press: New York, NY, USA, 2007. [Google Scholar]














Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plummer, S.; Pati, D.; Bhattacharya, A. Dynamics of Coordinate Ascent Variational Inference: A Case Study in 2D Ising Models. Entropy 2020, 22, 1263. https://doi.org/10.3390/e22111263
Plummer S, Pati D, Bhattacharya A. Dynamics of Coordinate Ascent Variational Inference: A Case Study in 2D Ising Models. Entropy. 2020; 22(11):1263. https://doi.org/10.3390/e22111263
Chicago/Turabian StylePlummer, Sean, Debdeep Pati, and Anirban Bhattacharya. 2020. "Dynamics of Coordinate Ascent Variational Inference: A Case Study in 2D Ising Models" Entropy 22, no. 11: 1263. https://doi.org/10.3390/e22111263
APA StylePlummer, S., Pati, D., & Bhattacharya, A. (2020). Dynamics of Coordinate Ascent Variational Inference: A Case Study in 2D Ising Models. Entropy, 22(11), 1263. https://doi.org/10.3390/e22111263




