The Effect of Catalogue Lead Time on Medium-Term Earthquake Forecasting with Application to New Zealand Data
Abstract
1. Introduction
2. Method and Data
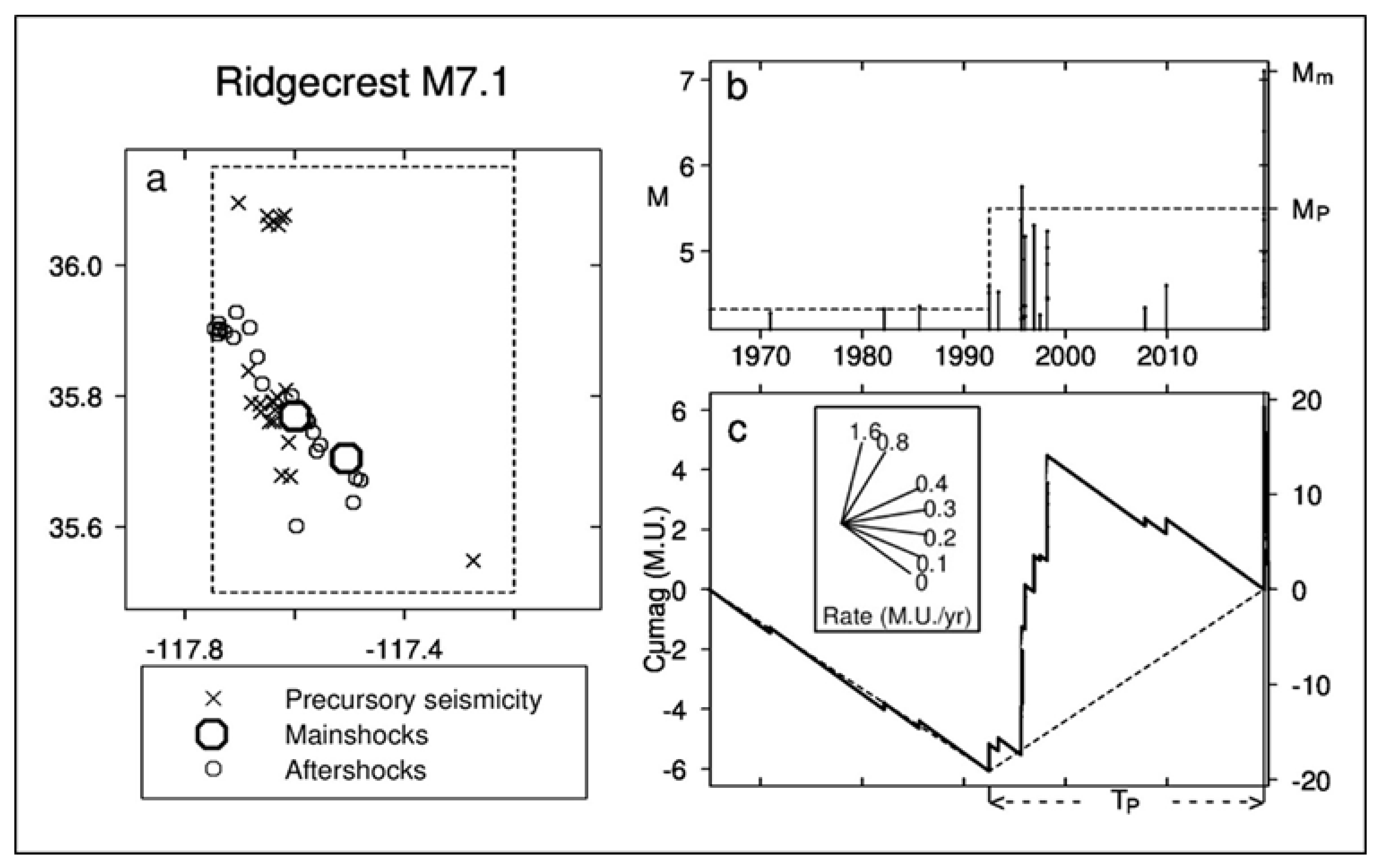
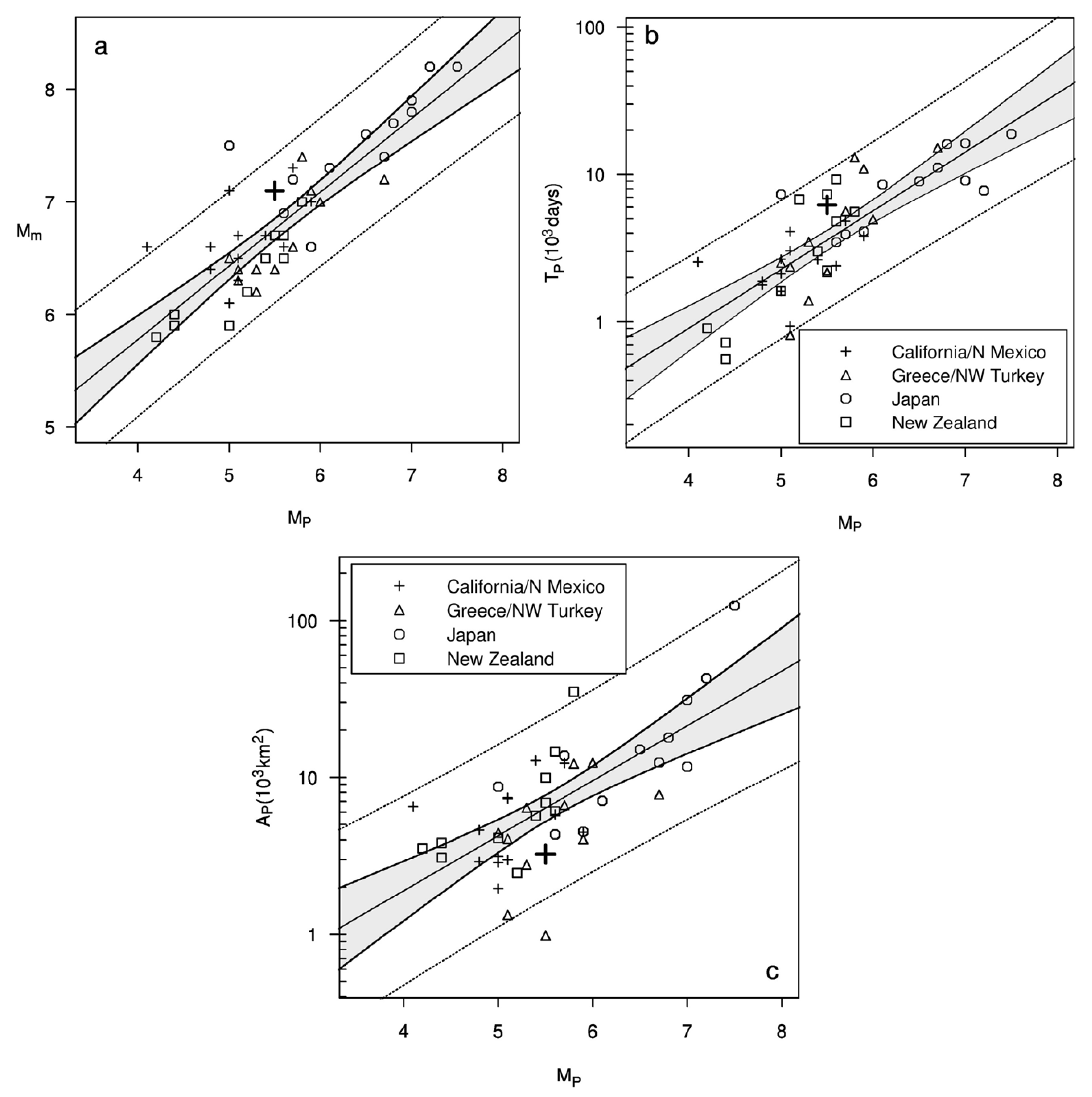
2.1. EEPAS Model Rate Density
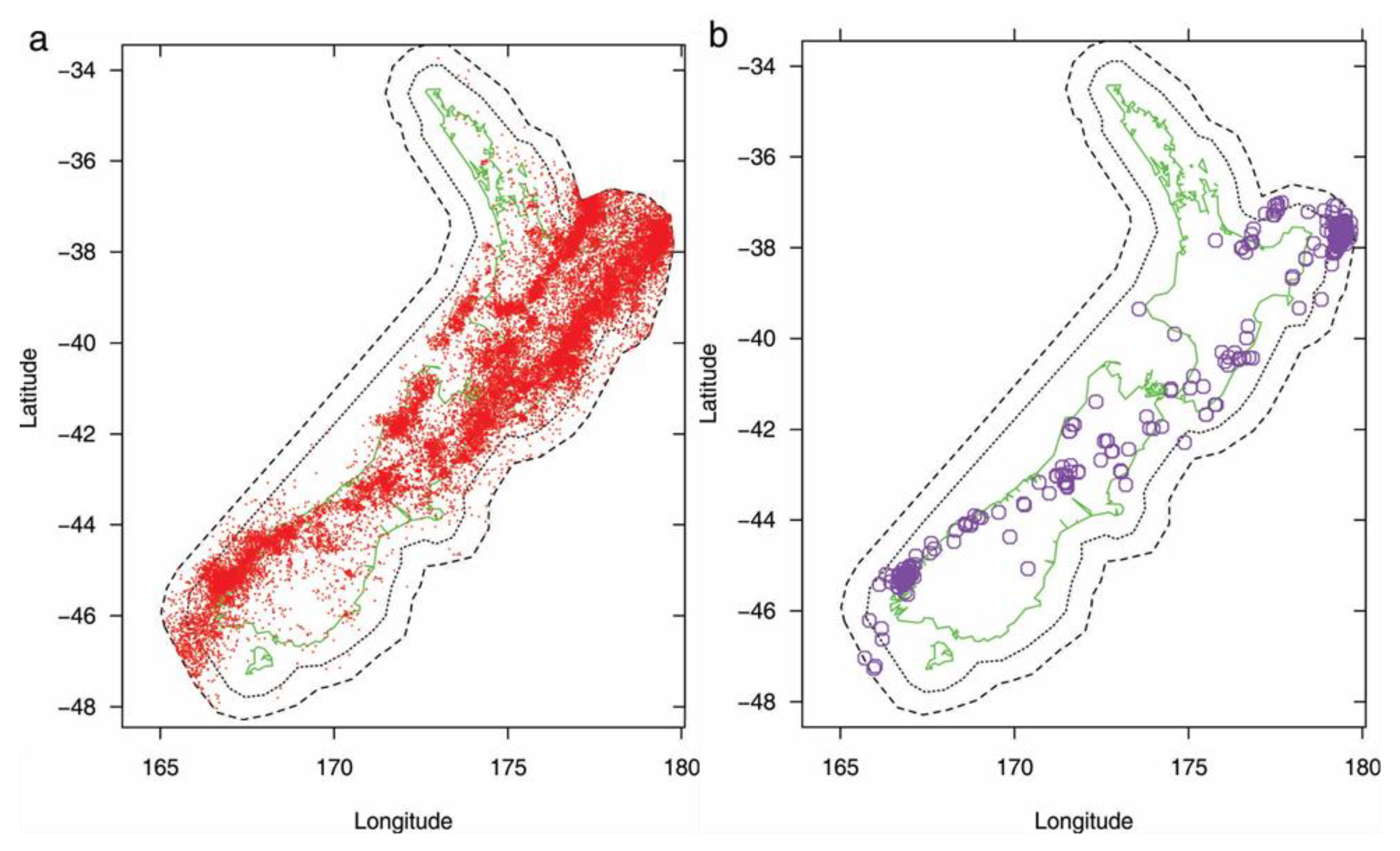
2.2. Data
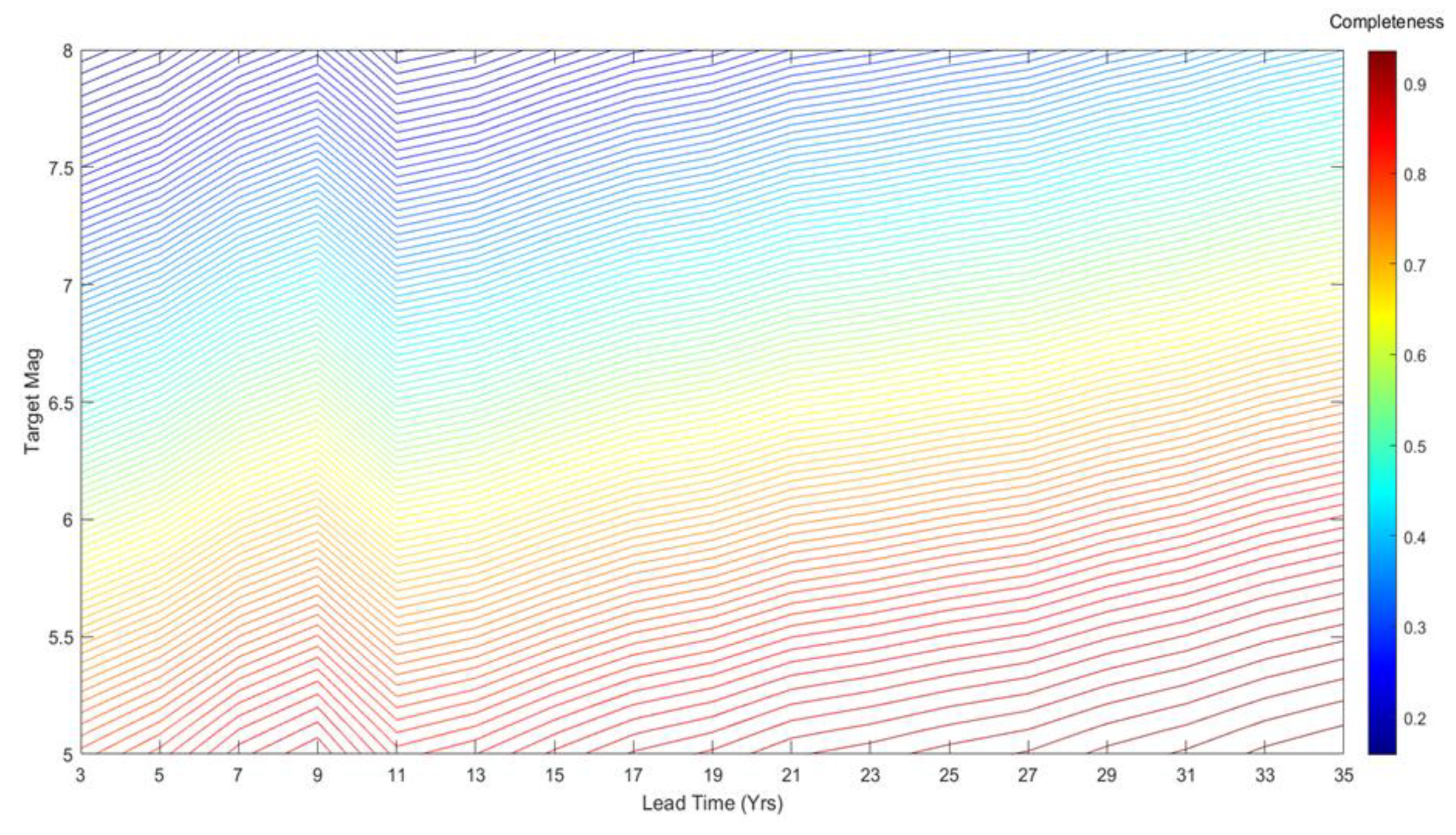
2.3. Completeness of Precursory Earthquake Contributions
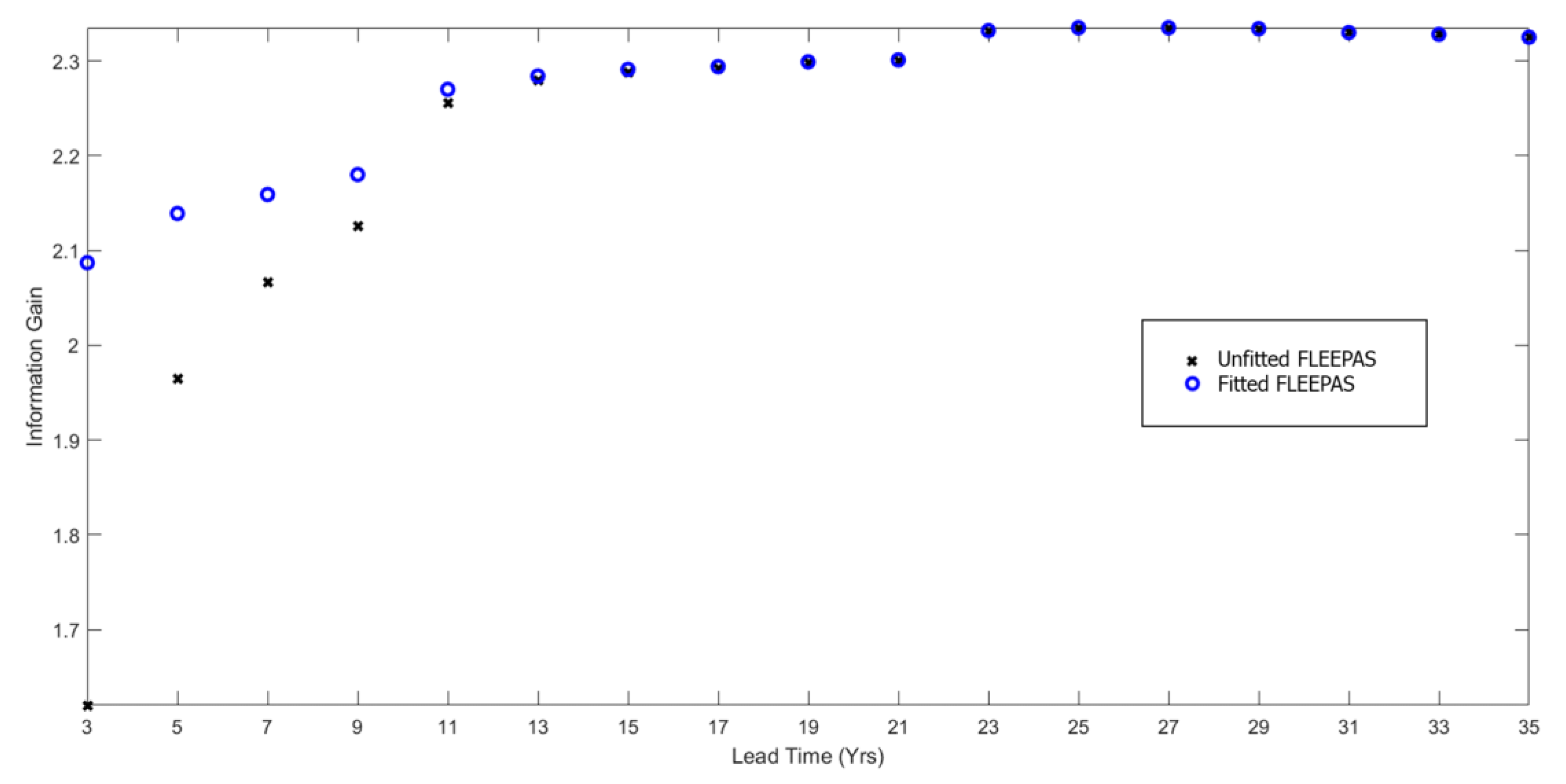
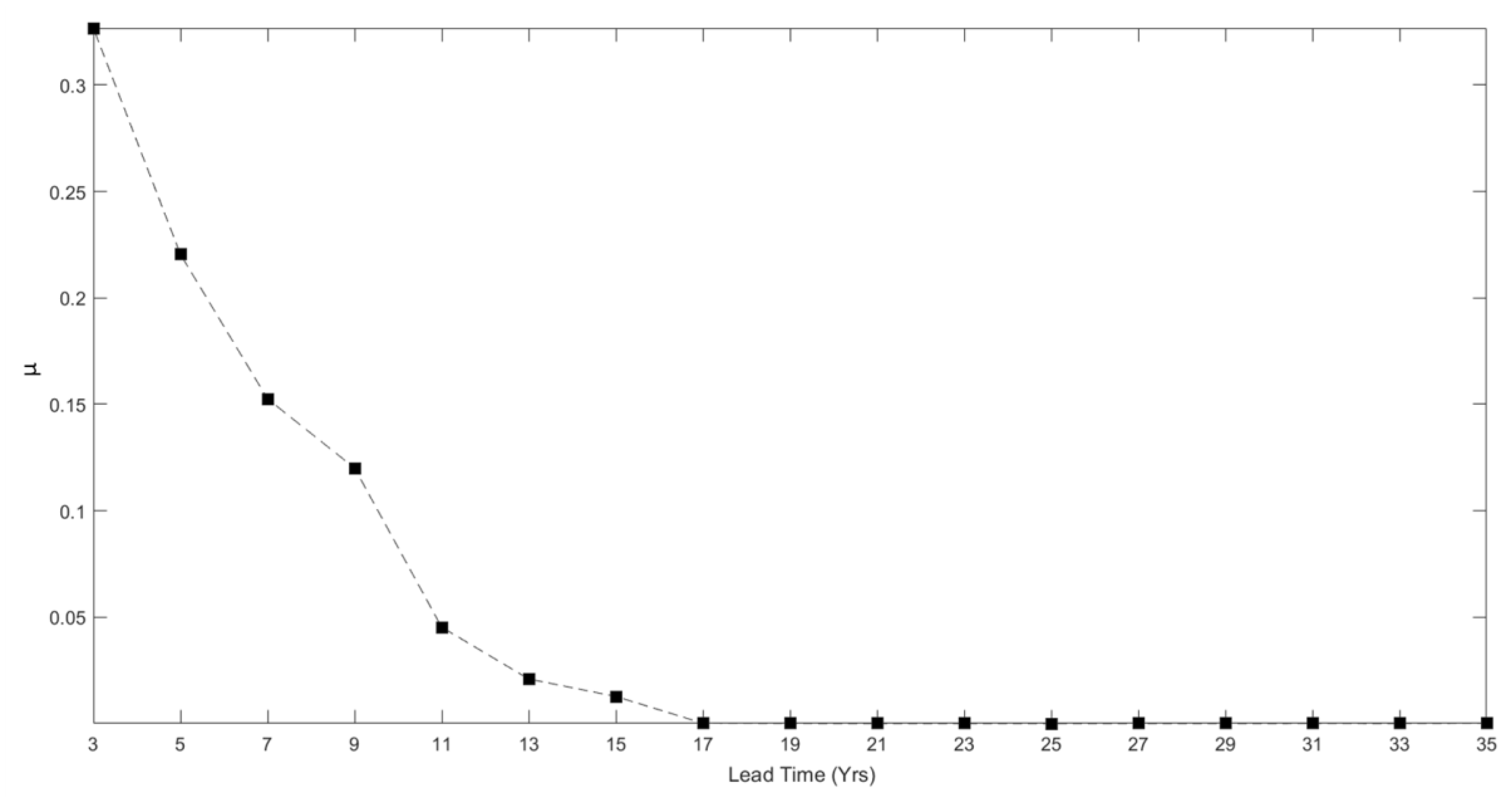
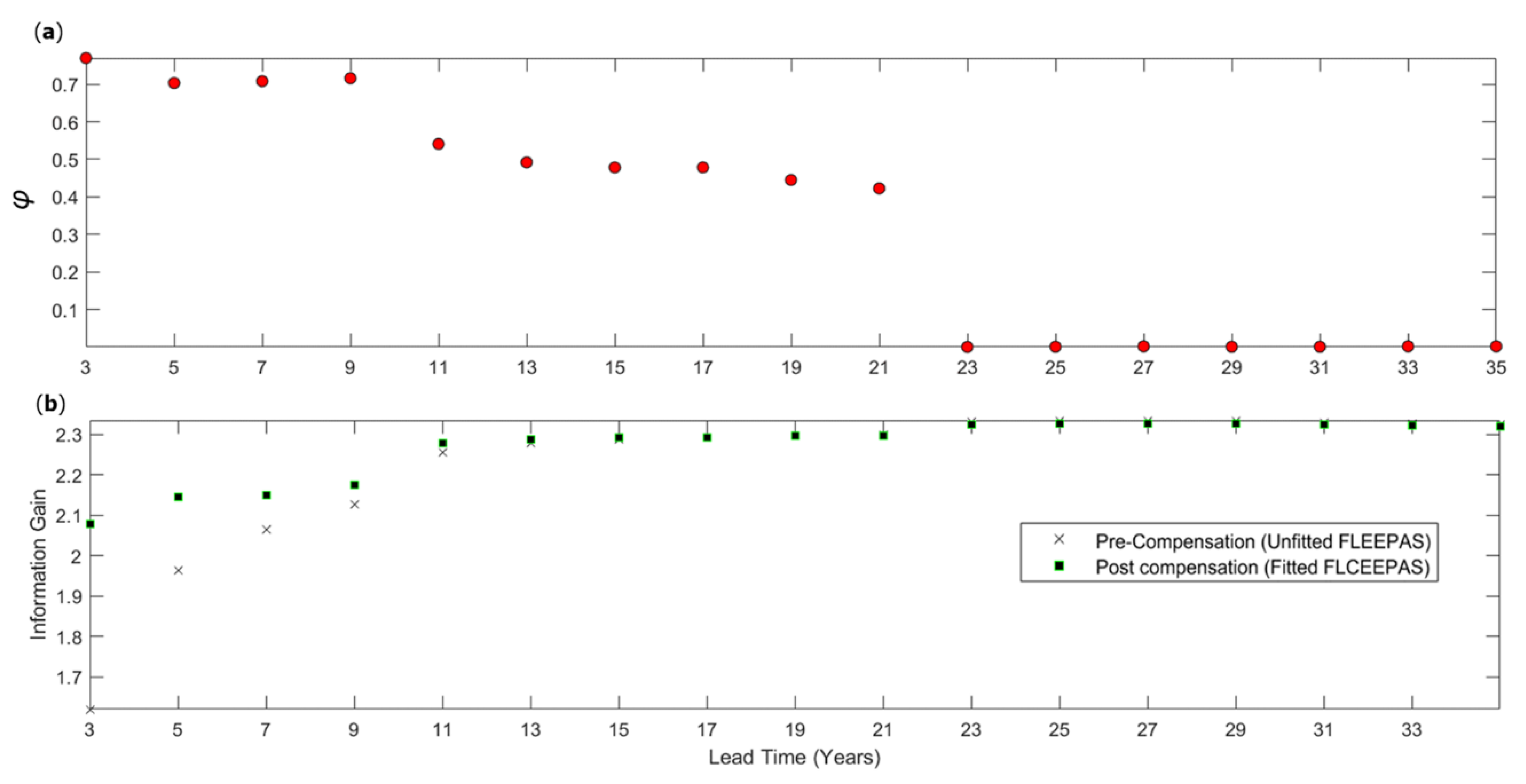
2.4. Compensating EEPAS for Incompleteness
2.4.1. Theory
2.4.2. Fixed Lead Time Compensated EEPAS Model
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rikitake, T. Classification of Earthquake Precursors. Tectonophysics 1979, 54, 293–309. [Google Scholar] [CrossRef]
- Ogata, Y. Statistical Models for Earthquake Occurrences and Residual Analysis for Point Processes. J. Am. Stat. Assoc. 1988, 83, 9–27. [Google Scholar] [CrossRef]
- Ogata, Y. Space-Time Point-Process Models for Earthquake Occurrences. Ann. Inst. Stat. Math. 1998, 50, 379–402. [Google Scholar] [CrossRef]
- Console, R.; Murru, M. A Simple and Testable Model for Earthquake Clustering. J. Geophys. Res. Space Phys. 2001, 106, 8699–8711. [Google Scholar] [CrossRef]
- Gerstenberger, M.C.; Wiemer, S.; Jones, L.M.; Reasenberg, P.A. Real-Time Forecasts of tomorrow’s Earthquakes in California. Nat. Cell Biol. 2005, 435, 328–331. [Google Scholar] [CrossRef] [PubMed]
- Ende, M.V.D.; Ampuero, J. On the Statistical Significance of Foreshock Sequences in Southern California. Geophys. Res. Lett. 2020, 47, 2019–086224. [Google Scholar] [CrossRef]
- Reasenberg, P.A. Foreshock Occurrence before Large Earthquakes. J. Geophys. Res. Space Phys. 1999, 104, 4755–4768. [Google Scholar] [CrossRef]
- Keilis-Borok, V.; Kossobokov, V. Premonitory Activation of Earthquake Flow: Algorithm M8. Phys. Earth Planet. Inter. 1990, 61, 73–83. [Google Scholar] [CrossRef]
- Kossobokov, V.G.; Keilis-Borok, V.I.; Smith, S.W. Localization of Intermediate-Term Earthquake Prediction. J. Geophys. Res. Space Phys. 1990, 95, 19763–19772. [Google Scholar] [CrossRef]
- Sobolev, G. Precursory Phases, Seismicity Precursors, and Earthquake Prediction in Kamchatka. Volcanol. Seismol. 1999, 20, 615–627. [Google Scholar]
- Jaume, S.C.; Sykes, L.R. Evolving Towards a Critical Point: A Review of Accelerating Seismic Moment/Energy Release Prior to Large and Great Earthquakes. Pure Appl. Geophys. PAGEOPH 1999, 155, 279–305. [Google Scholar] [CrossRef]
- Nanjo, K.; Rundle, J.B.; Holliday, J.; Turcotte, D.L. Pattern Informatics and Its Application for Optimal Forecasting of Large Earthquakes in Japan. Pure Appl. Geophys. PAGEOPH 2006, 163, 2417–2432. [Google Scholar] [CrossRef]
- Wyss, M.; Sobolev, G.; Clippard, J.D. Seismic Quiescence Precursors to Two M7 Earthquakes on Sakhalin Island, Measured by Two Methods. Earth Planets Space 2004, 56, 725–740. [Google Scholar] [CrossRef]
- Evison, F.; Rhoades, D. Precursory Scale Increase and Long-Term Seismogenesis in California and Northern Mexico. Ann. Geophys. 2002, 45, 479–495. [Google Scholar]
- Evison, F. The Precursory Earthquake Swarm. Phys. Earth Planet. Inter. 1977, 15, 19–23. [Google Scholar] [CrossRef]
- Evison, F. Generalised Precursory Swarm Hypothesis. J. Phys. Earth 1982, 30, 155–170. [Google Scholar] [CrossRef]
- Evison, F.F.; Rhoades, D. Demarcation and Scaling of Long-Term Seismogenesis. Pure Appl. Geophys. PAGEOPH 2004, 161, 21–45. [Google Scholar] [CrossRef]
- Ross, Z.E.; Idini, B.; Jia, Z.; Stephenson, O.L.; Zhong, M.; Wang, X.; Zhan, Z.; Simons, M.; Fielding, E.J.; Yun, S.-H.; et al. Hierarchical Interlocked Orthogonal Faulting in the 2019 Ridgecrest Earthquake Sequence. Science 2019, 366, 346–351. [Google Scholar] [CrossRef]
- Rhoades, D.; Evison, F.F. Long-Range Earthquake Forecasting With Every Earthquake a Precursor According to Scale. Pure Appl. Geophys. PAGEOPH 2004, 161, 47–72. [Google Scholar] [CrossRef]
- Rhoades, D.; Evison, F. The EEPAS Forecasting Model and the Probability of Moderate-to-Large Earthquakes in Central Japan. Tectonophysics 2006, 417, 119–130. [Google Scholar] [CrossRef]
- Rhoades, D.; Evison, F.F. Test of the EEPAS Forecasting Model on the Japan Earthquake Catalogue. Pure Appl. Geophys. PAGEOPH 2005, 162, 1271–1290. [Google Scholar] [CrossRef]
- Rhoades, D. Application of the EEPAS Model to Forecasting Earthquakes of Moderate Magnitude in Southern California. Seism. Res. Lett. 2007, 78, 110–115. [Google Scholar] [CrossRef]
- Console, R.; Rhoades, D.; Murru, M.; Evison, F.F.; Papadimitriou, E.; Karakostas, V.G. Comparative Performance of Time-Invariant, Long-Range and Short-Range Forecasting Models on the Earthquake Catalogue of Greece. J. Geophys. Res. Solid Earth 2006, 111, B09304. [Google Scholar] [CrossRef]
- Zechar, J.D.; Schorlemmer, D.; Liukis, M.; Yu, J.; Euchner, F.; Maechling, P.; Jordan, T.H. The Collaboratory for the Study of Earthquake Predictability Perspective on Computational Earthquake Science. Concurr. Comput. Pr. Exp. 2009, 22, 1836–1847. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Werner, M.J.; Marzocchi, W.; Jordan, T.H.; Ogata, Y.; Jackson, D.D.; Mak, S.; Rhoades, D.; Gerstenberger, M.C.; Hirata, N.; et al. The Collaboratory for the Study of Earthquake Predictability: Achievements and Priorities. Seism. Res. Lett. 2018, 89, 1305–1313. [Google Scholar] [CrossRef]
- Rhoades, D.; Christophersen, A.; Gerstenberger, M.C.; Liukis, M.; Silva, F.; Marzocchi, W.; Werner, M.J.; Jordan, T.H. Highlights from the First Ten Years of the New Zealand Earthquake Forecast Testing Center. Seism. Res. Lett. 2018, 89, 1229–1237. [Google Scholar] [CrossRef]
- Gerstenberger, M.C.; Rhoades, D.A.; McVerry, G.H. A Hybrid. Time-Dependent Probabilistic Seismic-Hazard. Model. For Canterbury, New Zealand. Seismol. Res. Lett. 2016, 87, 1311–1318. [Google Scholar] [CrossRef]
- Rhoades, D.; Christophersen, A. Time-Varying Probabilities of Earthquake Occurrence in Central New Zealand Based on the EEPAS Model Compensated for Time-Lag. Geophys. J. Int. 2019, 219, 417–429. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar]
- Gerstenberger, M.C.; Rhoades, D. New Zealand Earthquake Forecast Testing Centre. Pure Appl. Geophys. PAGEOPH 2010, 167, 877–892. [Google Scholar] [CrossRef]
- Rhoades, D. Mixture Models for Improved Earthquake Forecasting With Short-to-Medium Time Horizons. Bull. Seism. Soc. Am. 2013, 103, 2203–2215. [Google Scholar] [CrossRef]
- GeoNet. Earthquake Forecasts. Available online: https://www.geonet.org.nz/earthquake/Forecast/ (accessed on 14 September 2020).
- Harte, D.; Vere-Jones, D. The Entropy Score and Its Uses in Earthquake Forecasting. Pure Appl. Geophys. PAGEOPH 2005, 162, 1229–1253. [Google Scholar] [CrossRef]
- Rhoades, D.A.; Schorlemmer, D.; Gerstenberger, M.C.; Christophersen, A.; Zechar, J.D.; Imoto, M. Efficient Testing of Earthquake Forecasting Models. Acta Geophys. 2011, 59, 728–747. [Google Scholar] [CrossRef]
- Christophersen, A.; Rhoades, D.A.; Colella, H.V. Precursory Seismicity in Regions of Low Strain Rate: Insights from a Physics-Based Earthquake Simulator. Geophys. J. Int. 2017, 209, 1513–1525. [Google Scholar] [CrossRef]
- Marzocchi, W.; Zechar, J.D.; Jordan, T. Bayesian Forecast Evaluation and Ensemble Earthquake Forecasting. Bull. Seism. Soc. Am. 2012, 102, 2574–2584. [Google Scholar] [CrossRef]
- Imoto, M.; Rhoades, D. Seismicity Models of Moderate Earthquakes in Kanto, Japan Utilizing Multiple Predictive Parameters. Pure Appl. Geophys. PAGEOPH 2010, 167, 831–843. [Google Scholar] [CrossRef]
- Rhoades, D.; Gerstenberger, M.C.; Christophersen, A.; Zechar, J.D.; Schorlemmer, D.; Werner, M.J.; Jordan, T. Regional Earthquake Likelihood Models II: Information Gains of Multiplicative Hybrids. Bull. Seism. Soc. Am. 2014, 104, 3072–3083. [Google Scholar] [CrossRef]
- Bird, P.; Jackson, D.D.; Kagan, Y.Y.; Kreemer, C.; Stein, R.S. GEAR1: A Global Earthquake Activity Rate Model Constructed from Geodetic Strain Rates and Smoothed Seismicity. Bull. Seism. Soc. Am. 2015, 105, 2538–2554. [Google Scholar] [CrossRef]
- Rhoades, D.; Liukis, M.; Christophersen, A.; Gerstenberger, M.C. Retrospective Tests of Hybrid Operational Earthquake Forecasting Models for Canterbury. Geophys. J. Int. 2015, 204, 440–456. [Google Scholar] [CrossRef]


| Parameter | Details | EEPAS-0F |
|---|---|---|
| m0 | Minimum precursor magnitude | 2.95 * |
| mc | Minimum target magnitude | 4.95 * |
| mu | Maximum target magnitude | 8.05 * |
| bGR | Gutenberg–Richter b-value | 1.16 † |
| aM | Equation (5) | 1.10 † |
| bM | Equation (5) | 1.0 † |
| σM | Equation (5) | 0.39 † |
| aT | Equation (6) | 1.73 |
| bT | Equation (6) | 0.39 † |
| σT | Equation (6) | 0.60 † |
| bA | Equation (7) | 0.36 † |
| σA | Equation (7) | 1.53 |
| μ | Equation (8) | 3.6 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rhoades, D.A.; J. Rastin, S.; Christophersen, A. The Effect of Catalogue Lead Time on Medium-Term Earthquake Forecasting with Application to New Zealand Data. Entropy 2020, 22, 1264. https://doi.org/10.3390/e22111264
Rhoades DA, J. Rastin S, Christophersen A. The Effect of Catalogue Lead Time on Medium-Term Earthquake Forecasting with Application to New Zealand Data. Entropy. 2020; 22(11):1264. https://doi.org/10.3390/e22111264
Chicago/Turabian StyleRhoades, David A., Sepideh J. Rastin, and Annemarie Christophersen. 2020. "The Effect of Catalogue Lead Time on Medium-Term Earthquake Forecasting with Application to New Zealand Data" Entropy 22, no. 11: 1264. https://doi.org/10.3390/e22111264
APA StyleRhoades, D. A., J. Rastin, S., & Christophersen, A. (2020). The Effect of Catalogue Lead Time on Medium-Term Earthquake Forecasting with Application to New Zealand Data. Entropy, 22(11), 1264. https://doi.org/10.3390/e22111264







