Testing of Multifractional Brownian Motion
Abstract
1. Introduction
2. Model and Methods
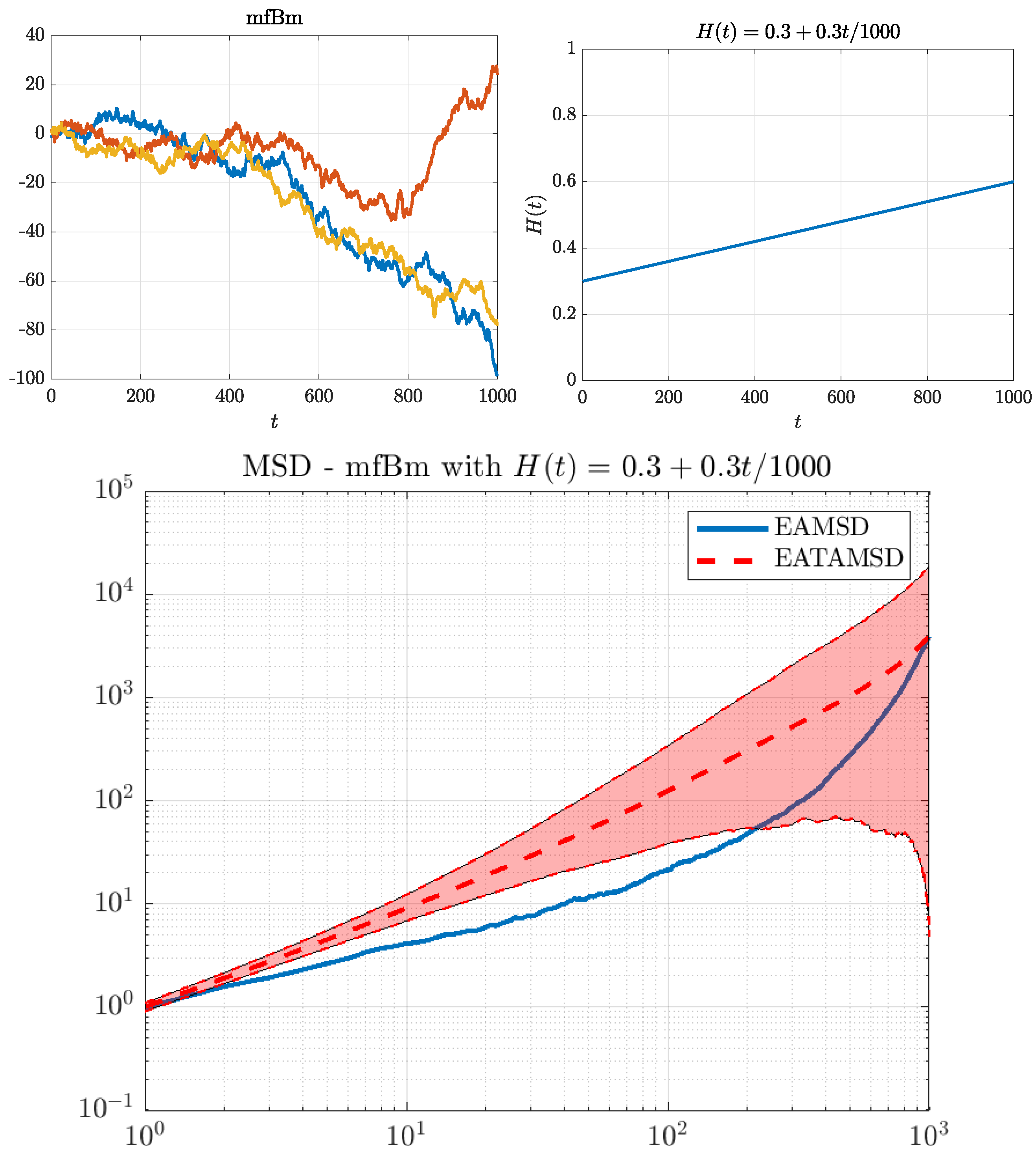
2.1. Mean-Squared Displacement
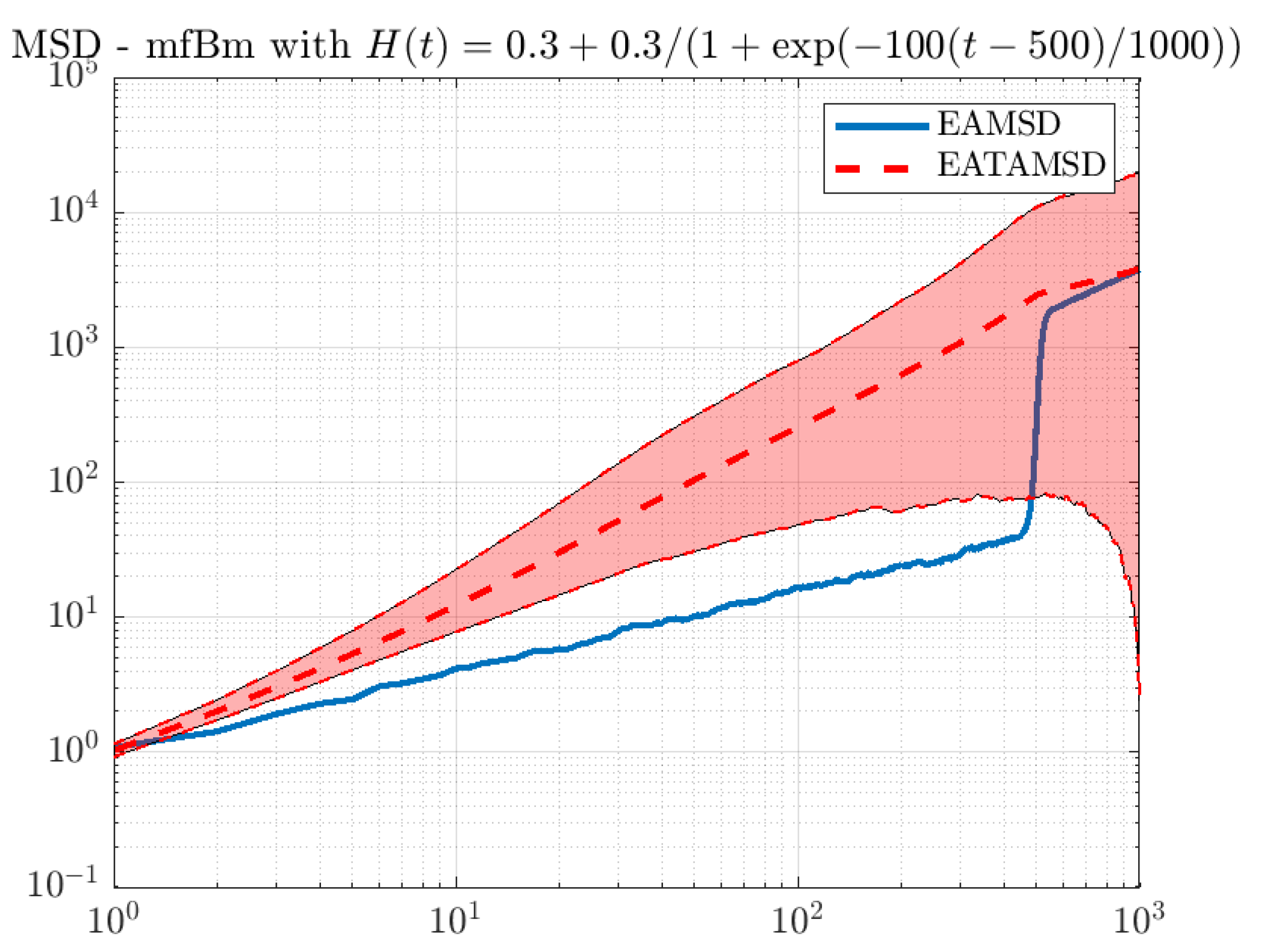
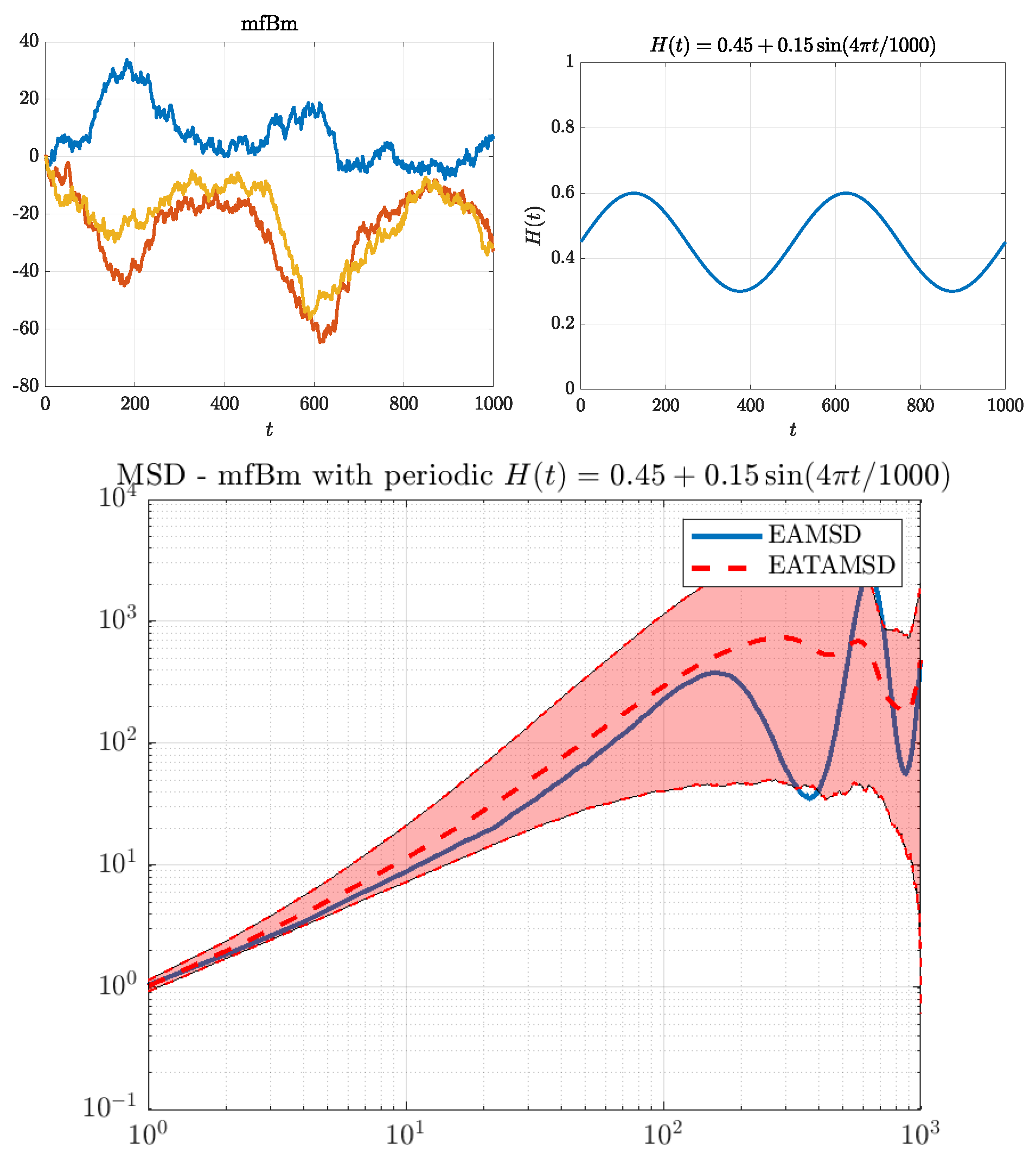
2.2. Three Cases of the Hurst Exponent Function
3. Results
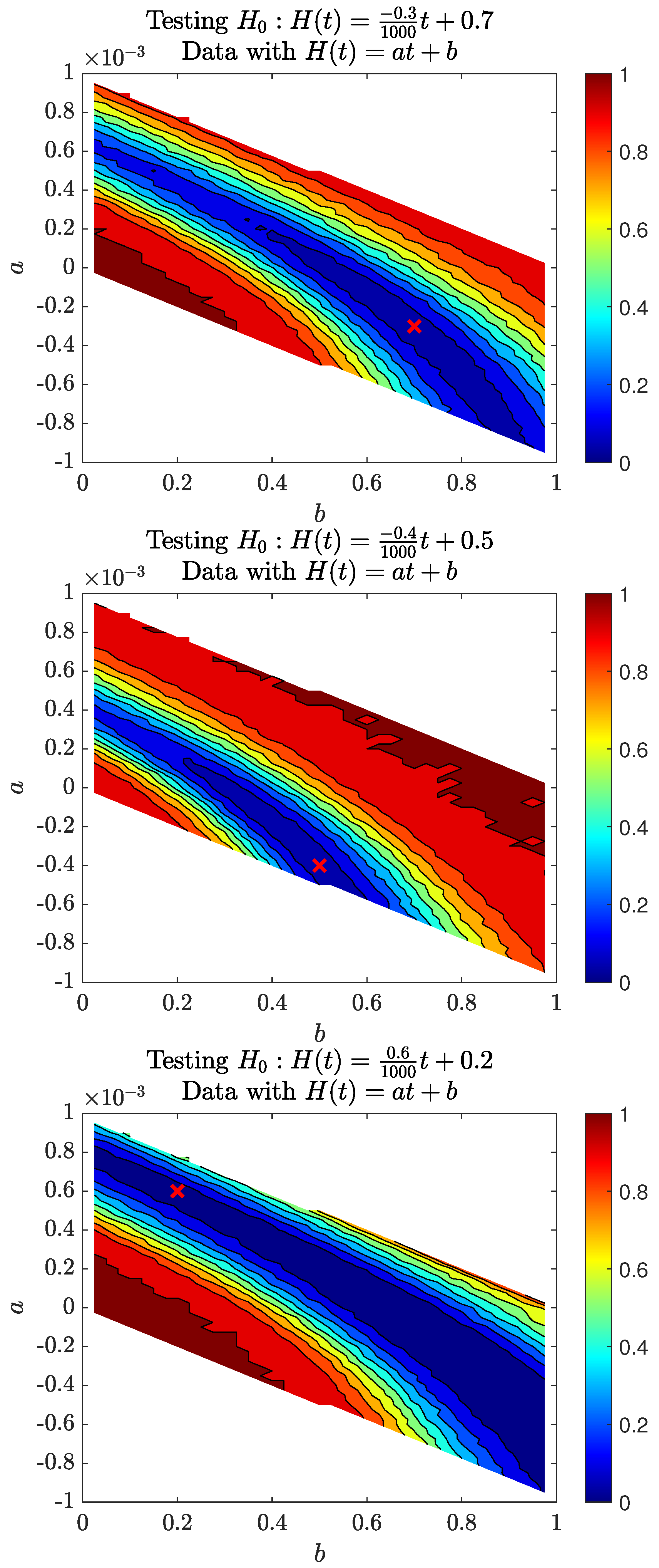
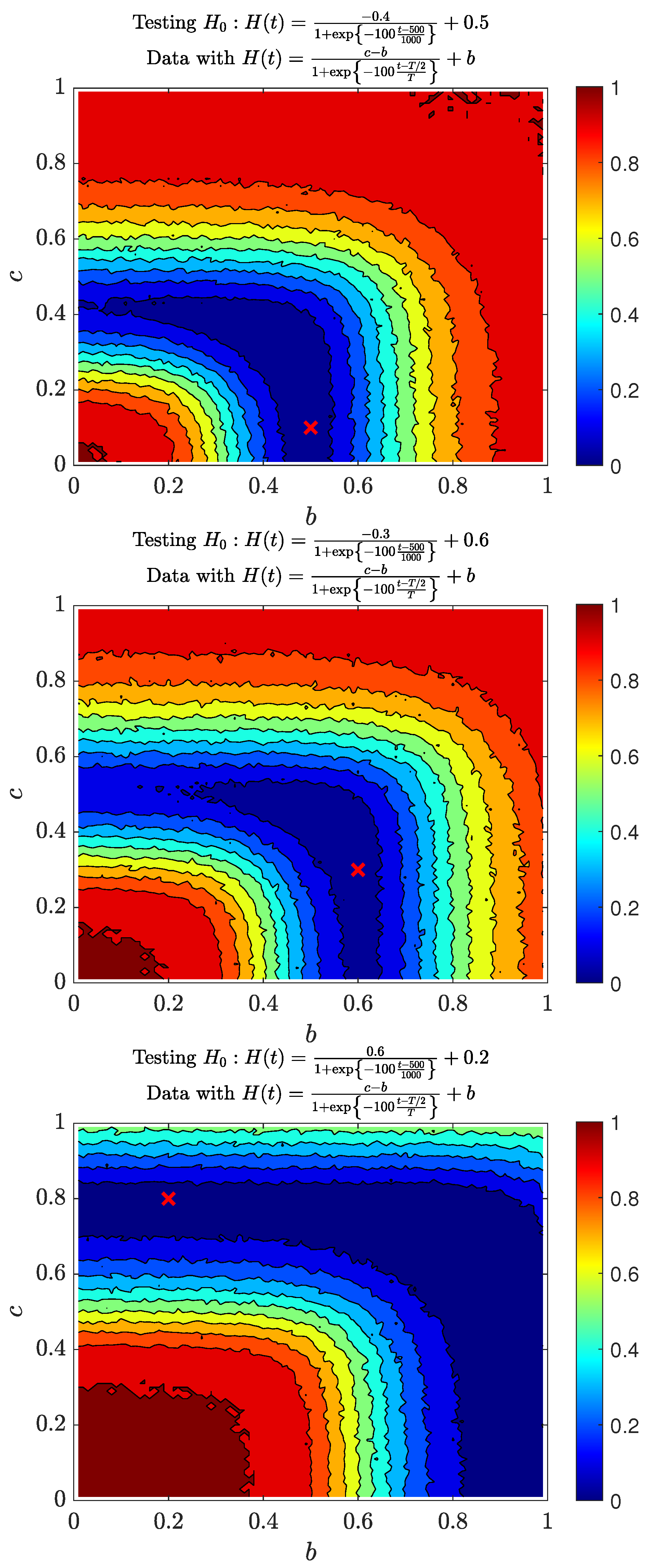
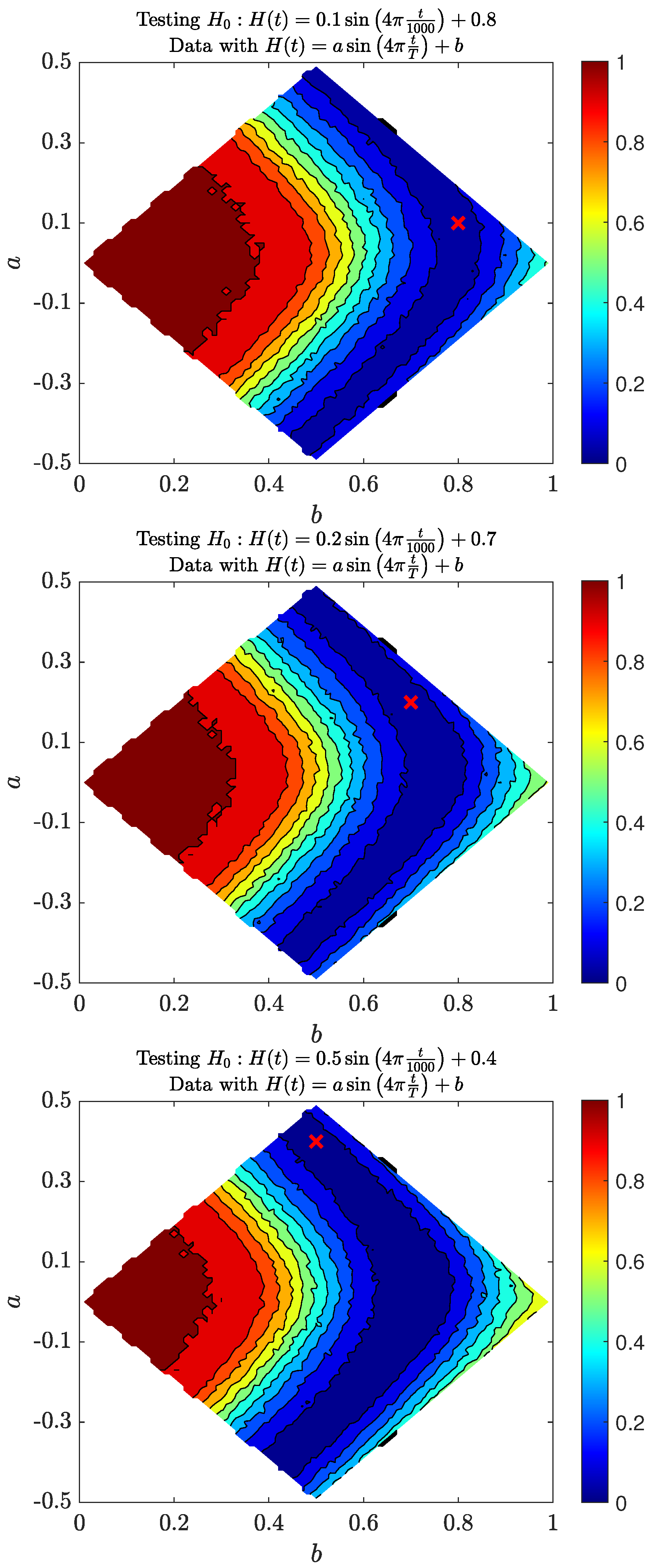
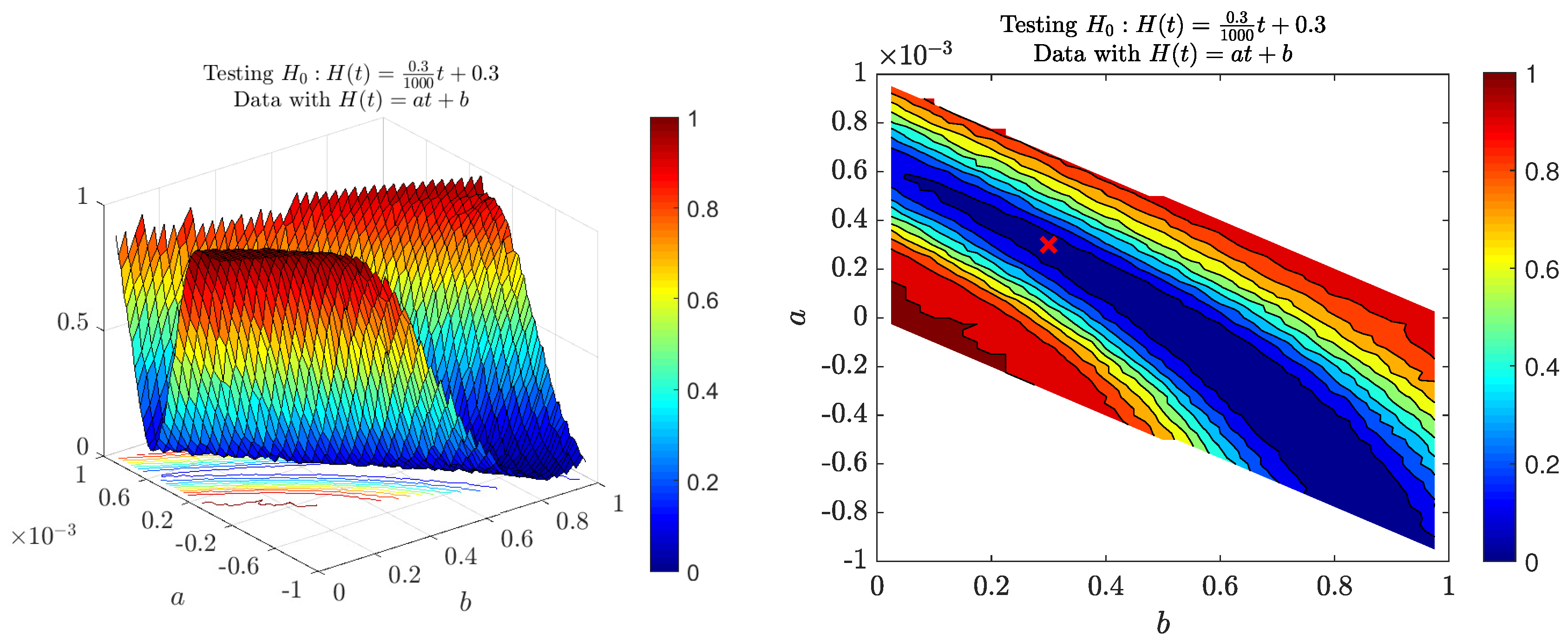
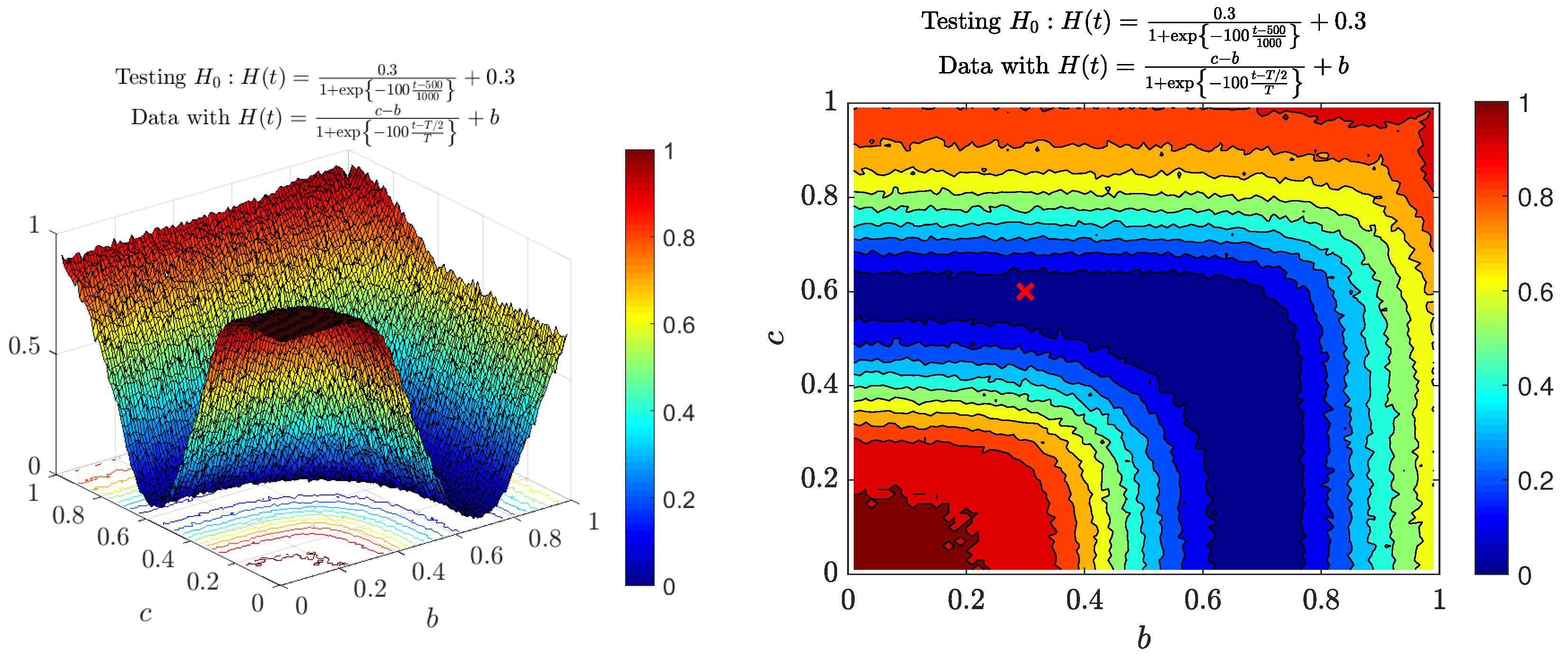
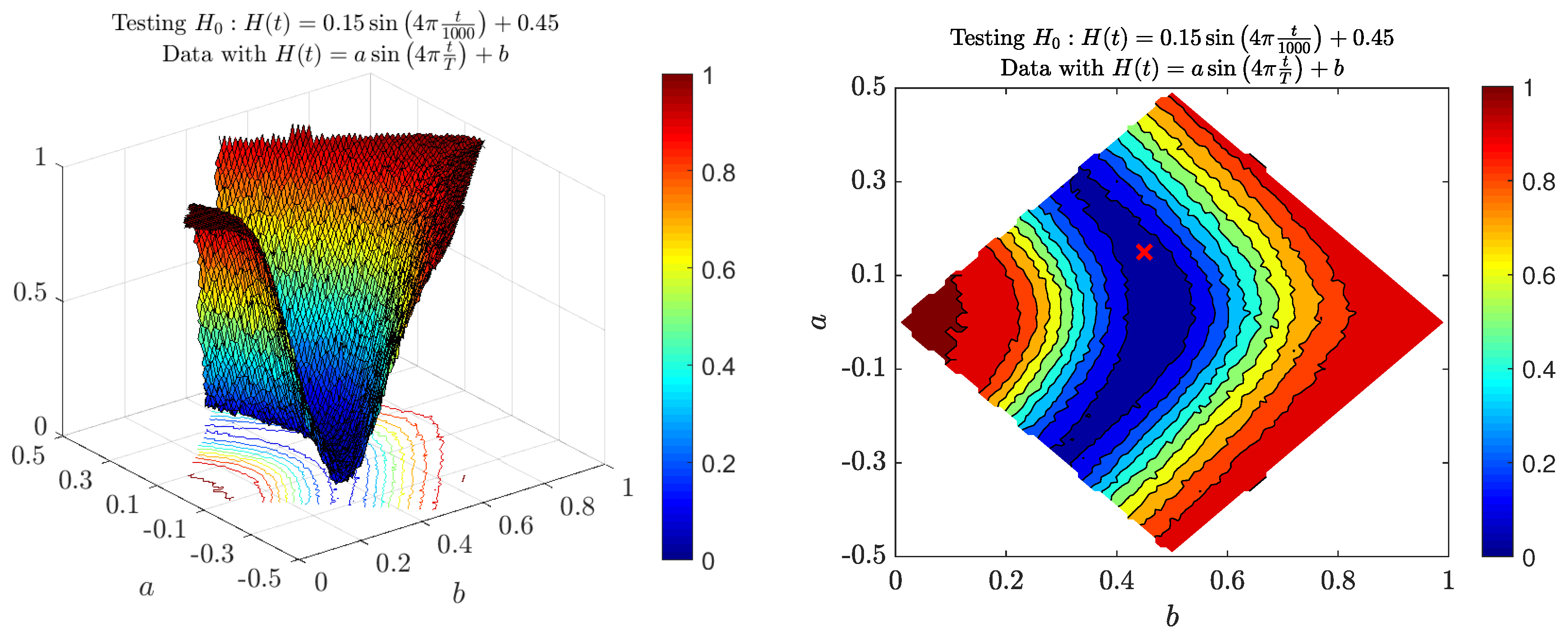
3.1. Test
3.2. Three Power Case Studies
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SPT | Single-particle tracking |
| FBM | Fractional Brownian motion |
| MFBM | Multifractional Brownian motion |
| MSD | Mean-squared displacement |
| TAMSD | Time average mean-squared displacement |
| EAMSD | Ensemble average mean-squared displacement |
| EATAMSD | Ensemble and time average mean-squared displacement |
| ACVF | Autocovariance function |
Appendix A
References
- Braüchle, C.; Lamb, D.C.; Michaelis, J. Single Particle Tracking and Single Molecule Energy Transfer; Wiley-VCH: Weinheim, Germany, 2010. [Google Scholar]
- Xie, X.S.; Choi, P.J.; Li, G.W.; Lee, N.K.; Lia, G. Single-molecule approach to molecular biology in living bacterial cells. Annu. Rev. Biophys. 2008, 37, 417–444. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Jeon, J.H.; Cherstvy, A. Non-Brownian diffusion in lipid membranes: Experiments and simulations. Biochim. Biophys. Acta (BBA)-Biomembr. 2016, 1858, 2451–2467. [Google Scholar] [CrossRef] [PubMed]
- Saxton, M.J.; Jacobson, K. Single-particle tracking: Applications to membrane dynamics. Annu. Rev. Biophys. Biomol. Struct. 1997, 26, 373–399. [Google Scholar] [CrossRef] [PubMed]
- Bouchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Höfling, F.; Franosch, T. Anomalous transport in the crowded world of biological cells. Rep. Prog. Phys. 2013, 76, 046602. [Google Scholar] [CrossRef] [PubMed]
- Barkai, E.; Garini, Y.; Metzler, R. Strange kinetics of single molecules in living cells. Phys. Today 2012, 65, 29. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef]
- Golding, I.; Cox, E.C. Physical nature of bacterial cytoplasm. Phys. Rev. Lett. 2006, 96, 098102. [Google Scholar] [CrossRef]
- Bronstein, I.; Israel, Y.; Kepten, E.; Mai, S.; Shav-Tal, Y.; Barkai, E.; Garini, Y. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys. Rev. Lett. 2009, 103, 018102. [Google Scholar] [CrossRef]
- Jeon, J.H.; Tejedor, V.; Burov, S.; Barkai, E.; Selhuber-Unkel, C.; Berg-Sørensen, K.; Oddershede, L.; Metzler, R. In vivo anomalous diffusion and weak ergodicity breaking of lipid granules. Phys. Rev. Lett. 2011, 106, 048103. [Google Scholar] [CrossRef]
- Weigel, A.V.; Simon, B.; Tamkun, M.M.; Krapf, D. Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking. Proc. Natl. Acad. Sci. USA 2011, 108, 6438–6443. [Google Scholar] [CrossRef] [PubMed]
- Tabei, S.A.; Burov, S.; Kim, H.Y.; Kuznetsov, A.; Huynh, T.; Jureller, J.; Philipson, L.H.; Dinner, A.R.; Scherer, N.F. Intracellular transport of insulin granules is a subordinated random walk. Proc. Natl. Acad. Sci. USA 2013, 110, 4911–4916. [Google Scholar] [CrossRef] [PubMed]
- Szymanski, J.; Weiss, M. Elucidating the origin of anomalous diffusion in crowded fluids. Phys. Rev. Lett. 2009, 103, 038102. [Google Scholar] [CrossRef] [PubMed]
- Jeon, J.H.; Leijnse, N.; Oddershede, L.B.; Metzler, R. Anomalous diffusion and power-law relaxation of the time averaged mean squared displacement in worm-like micellar solutions. New J. Phys. 2013, 15, 045011. [Google Scholar] [CrossRef]
- Wong, I.; Gardel, M.; Reichman, D.; Weeks, E.R.; Valentine, M.; Bausch, A.; Weitz, D.A. Anomalous diffusion probes microstructure dynamics of entangled F-actin networks. Phys. Rev. Lett. 2004, 92, 178101. [Google Scholar] [CrossRef] [PubMed]
- Hansing, J.; Ciemer, C.; Kim, W.K.; Zhang, X.; DeRouchey, J.E.; Netz, R.R. Nanoparticle filtering in charged hydrogels: Effects of particle size, charge asymmetry and salt concentration. Eur. Phys. J. E 2016, 39, 53. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Feng, L.; Sha, R.; Seeman, N.; Chaikin, P. Subdiffusion of a sticky particle on a surface. Phys. Rev. Lett. 2011, 106, 228102. [Google Scholar] [CrossRef]
- Godec, A.; Bauer, M.; Metzler, R. Collective dynamics effect transient subdiffusion of inert tracers in flexible gel networks. New J. Phys. 2014, 16, 092002. [Google Scholar] [CrossRef]
- Weiss, M.; Hashimoto, H.; Nilsson, T. Anomalous protein diffusion in living cells as seen by fluorescence correlation spectroscopy. Biophys. J. 2003, 84, 4043–4052. [Google Scholar] [CrossRef]
- Kneller, G.R.; Baczynski, K.; Pasenkiewicz-Gierula, M. Communication: Consistent picture of lateral subdiffusion in lipid bilayers: Molecular dynamics simulation and exact results. J. Chem. Phys. 2011, 135, 141105. [Google Scholar] [CrossRef]
- Jeon, J.H.; Monne, H.M.S.; Javanainen, M.; Metzler, R. Anomalous diffusion of phospholipids and cholesterols in a lipid bilayer and its origins. Phys. Rev. Lett. 2012, 109, 188103. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, E.; Akimoto, T.; Yasui, M.; Yasuoka, K. Origin of subdiffusion of water molecules on cell membrane surfaces. Sci. Rep. 2014, 4, 4720. [Google Scholar] [CrossRef] [PubMed]
- Manzo, C.; Torreno-Pina, J.A.; Massignan, P.; Lapeyre, G.J., Jr.; Lewenstein, M.; Parajo, M.F.G. Weak ergodicity breaking of receptor motion in living cells stemming from random diffusivity. Phys. Rev. X 2015, 5, 011021. [Google Scholar] [CrossRef]
- Jeon, J.H.; Javanainen, M.; Martinez-Seara, H.; Metzler, R.; Vattulainen, I. Protein crowding in lipid bilayers gives rise to non-Gaussian anomalous lateral diffusion of phospholipids and proteins. Phys. Rev. X 2016, 6, 021006. [Google Scholar] [CrossRef]
- Berkowitz, B.; Cortis, A.; Dentz, M.; Scher, H. Modeling non-Fickian transport in geological formations as a continuous time random walk. Rev. Geophys. 2006, 44. [Google Scholar] [CrossRef]
- Caspi, A.; Granek, R.; Elbaum, M. Enhanced diffusion in active intracellular transport. Phys. Rev. Lett. 2000, 85, 5655. [Google Scholar] [CrossRef]
- Reverey, J.F.; Jeon, J.H.; Bao, H.; Leippe, M.; Metzler, R.; Selhuber-Unkel, C. Superdiffusion dominates intracellular particle motion in the supercrowded cytoplasm of pathogenic Acanthamoeba castellanii. Sci. Rep. 2015, 5, 1–14. [Google Scholar] [CrossRef]
- Gal, N.; Weihs, D. Experimental evidence of strong anomalous diffusion in living cells. Phys. Rev. E 2010, 81, 020903. [Google Scholar] [CrossRef]
- Monserud, J.H.; Schwartz, D.K. Interfacial molecular searching using forager dynamics. Phys. Rev. Lett. 2016, 116, 098303. [Google Scholar] [CrossRef]
- Campagnola, G.; Nepal, K.; Schroder, B.W.; Peersen, O.B.; Krapf, D. Superdiffusive motion of membrane-targeting C2 domains. Sci. Rep. 2015, 5, 1–10. [Google Scholar] [CrossRef]
- Javanainen, M.; Hammaren, H.; Monticelli, L.; Jeon, J.H.; Miettinen, M.S.; Martinez-Seara, H.; Metzler, R.; Vattulainen, I. Anomalous and normal diffusion of proteins and lipids in crowded lipid membranes. Faraday Discuss. 2013, 161, 397–417. [Google Scholar] [CrossRef] [PubMed]
- Kolmogorov, A.N. Wienersche Spiralen und einige andere interessante Kurven in Hilbertscen Raum. C.R. (Dokl.) Acad. Sci. URSS (NS) 1940, 26, 115–118. [Google Scholar]
- Mandelbrot, B.B.; Van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Graves, T.; Gramacy, R.; Watkins, N.; Franzke, C. A brief history of long memory: Hurst, Mandelbrot and the road to ARFIMA, 1951–1980. Entropy 2017, 19, 437. [Google Scholar] [CrossRef]
- Goychuk, I. Viscoelastic subdiffusion: Generalized Langevin equation approach. Adv. Chem. Phys. 2012, 150, 187. [Google Scholar]
- Klafter, J.; Lim, S.; Metzler, R. Fractional Dynamics: Recent Advances; World Scientific: Singapore, 2012. [Google Scholar]
- Balcerek, M.; Burnecki, K. Testing of fractional Brownian motion in a noisy environment. Chaos Solitons Fractals 2020, 140, 110097. [Google Scholar] [CrossRef]
- Sikora, G.; Burnecki, K.; Wyłomańska, A. Mean-squared displacement statistical test for fractional Brownian motion. Phys. Rev. E 2017, 95, 032110. [Google Scholar] [CrossRef]
- Sikora, G. Statistical test for fractional Brownian motion based on detrending moving average algorithm. Chaos Solitons Fractals 2018, 114, 54–62. [Google Scholar] [CrossRef]
- Ralchenko, K.; Shevchenko, G. Path properties of multifractal Brownian motion. Theory Probab. Math. Stat. 2010, 80, 119–130. [Google Scholar] [CrossRef]
- Peltier, R.F.; Véhel, J.L. Multifractional Brownian Motion: Definition and Preliminary Results; Research Report, RR-2645 INRIA, 1995. Ffinria-00074045; Inria Paris: Rocquencourt, France, 1995. [Google Scholar]
- Lee, K. Characterization of turbulence stability through the identification of multifractional Brownian motions. Nonlinear Process. Geophys. 2013, 20, 97–106. [Google Scholar] [CrossRef]
- Perrin, E.; Harba, R.; Iribarren, I.; Jennane, R. Piecewise fractional Brownian motion. IEEE Trans. Signal Process. 2005, 53, 1211–1215. [Google Scholar] [CrossRef]
- Ryvkina, J. Fractional Brownian Motion with variable Hurst parameter: Definition and properties. J. Theor. Probab. 2015, 28, 866–891. [Google Scholar] [CrossRef]
- Ayache, A.; Cohen, S.; Véhel, J.L. The covariance structure of multifractional Brownian motion, with application to long range dependence. In Proceedings of the 2000 IEEE International Conference on Acoustics, Speech, and Signal Processing, Istanbul, Turkey, 5–9 June 2000; Volume 6, pp. 3810–3813. [Google Scholar]
- Benassi, A.; Cohen, S.; Istas, J. Identifying the multifractional function of a Gaussian process. Stat. Probab. Lett. 1998, 39, 337–345. [Google Scholar] [CrossRef]
- Chan, G.; Wood, A.T. Simulation of multifractional Brownian motion. In COMPSTAT; Springer: Berlin/Heidelberg, Germany, 1998; pp. 233–238. [Google Scholar]
- Stoev, S.A.; Taqqu, M.S. How rich is the class of multifractional Brownian motions? Stoch. Process. Appl. 2006, 116, 200–221. [Google Scholar] [CrossRef]
- Bianchi, S. Pathwise identification of the memory function of multifractional Brownian motion with application to finance. Int. J. Theor. Appl. Financ. 2005, 8, 255–281. [Google Scholar] [CrossRef]
- Bardet, J.M.; Bertrand, P. Identification of the multiscale fractional Brownian motion with biomechanical applications. J. Time Ser. Anal. 2007, 28, 1–52. [Google Scholar] [CrossRef]
- Bianchi, S.; Pantanella, A.; Pianese, A. Modeling stock prices by multifractional Brownian motion: An improved estimation of the pointwise regularity. Quant. Financ. 2013, 13, 1317–1330. [Google Scholar] [CrossRef]
- Pianese, A.; Bianchi, S.; Palazzo, A.M. Fast and unbiased estimator of the time-dependent Hurst exponent. Chaos Interdiscip. J. Nonlinear Sci. 2018, 28, 031102. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balcerek, M.; Burnecki, K. Testing of Multifractional Brownian Motion. Entropy 2020, 22, 1403. https://doi.org/10.3390/e22121403
Balcerek M, Burnecki K. Testing of Multifractional Brownian Motion. Entropy. 2020; 22(12):1403. https://doi.org/10.3390/e22121403
Chicago/Turabian StyleBalcerek, Michał, and Krzysztof Burnecki. 2020. "Testing of Multifractional Brownian Motion" Entropy 22, no. 12: 1403. https://doi.org/10.3390/e22121403
APA StyleBalcerek, M., & Burnecki, K. (2020). Testing of Multifractional Brownian Motion. Entropy, 22(12), 1403. https://doi.org/10.3390/e22121403




