Artificial Intelligence for Modeling Real Estate Price Using Call Detail Records and Hybrid Machine Learning Approach
Abstract
:1. Introduction
2. Materials and Methods
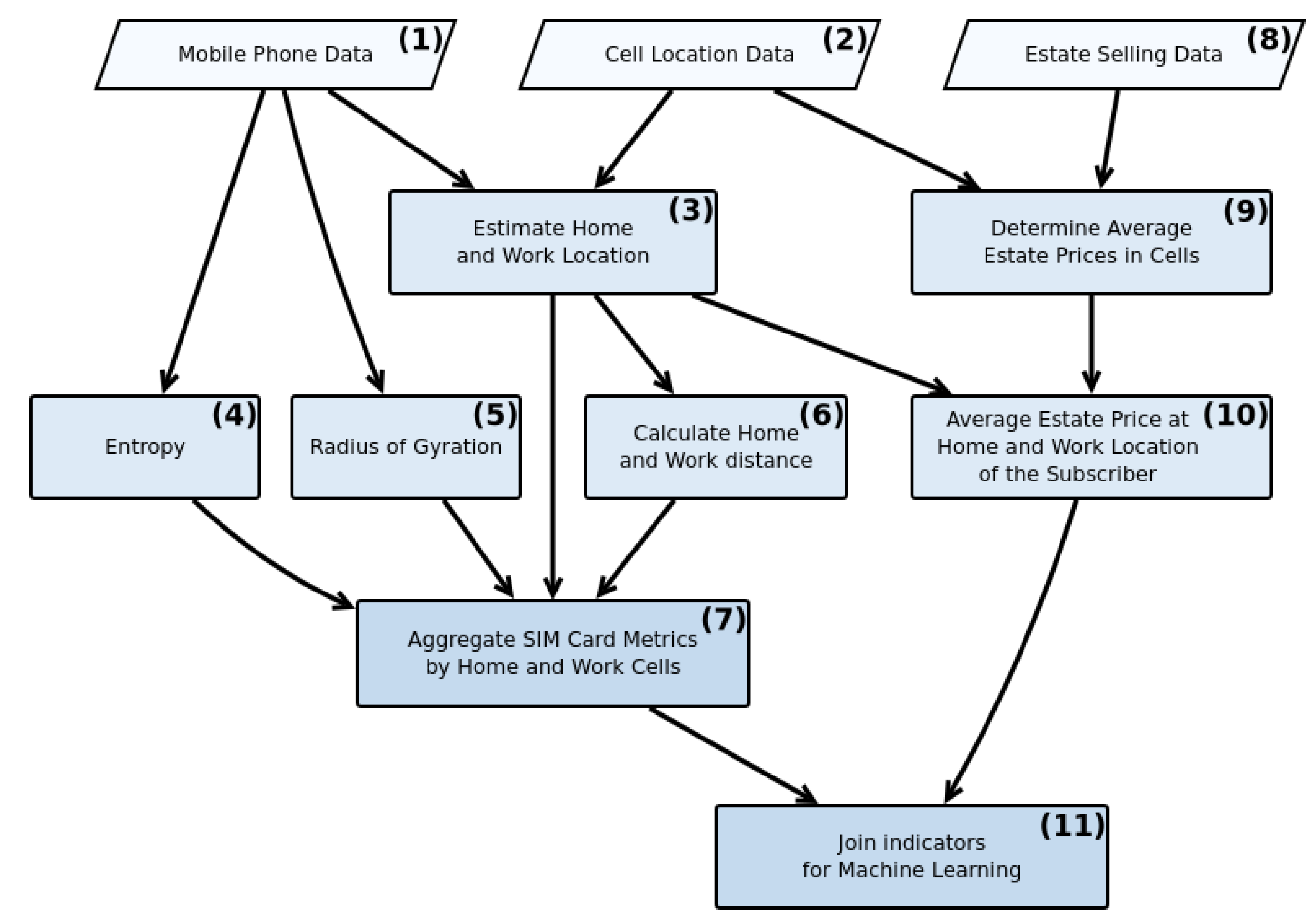
2.1. Data
- Norm price: normalized real estate price;
- Dweller entropy: mean entropy of the devices whose home is the given cell;
- Dweller gyration: mean gyration of the devices whose home is the given cell;
- Worker entropy: mean entropy of the devices whose workplace is the given cell;
- Worker gyration: mean gyration of the devices whose workplace is the given cell;
- Dwellers’ home distance: average work-home distance of the devices whose home cell is the given cell;
- Workers’ work distance: average work-home distance of the devices whose work cell is the given cell.
2.2. Methods
3. Results
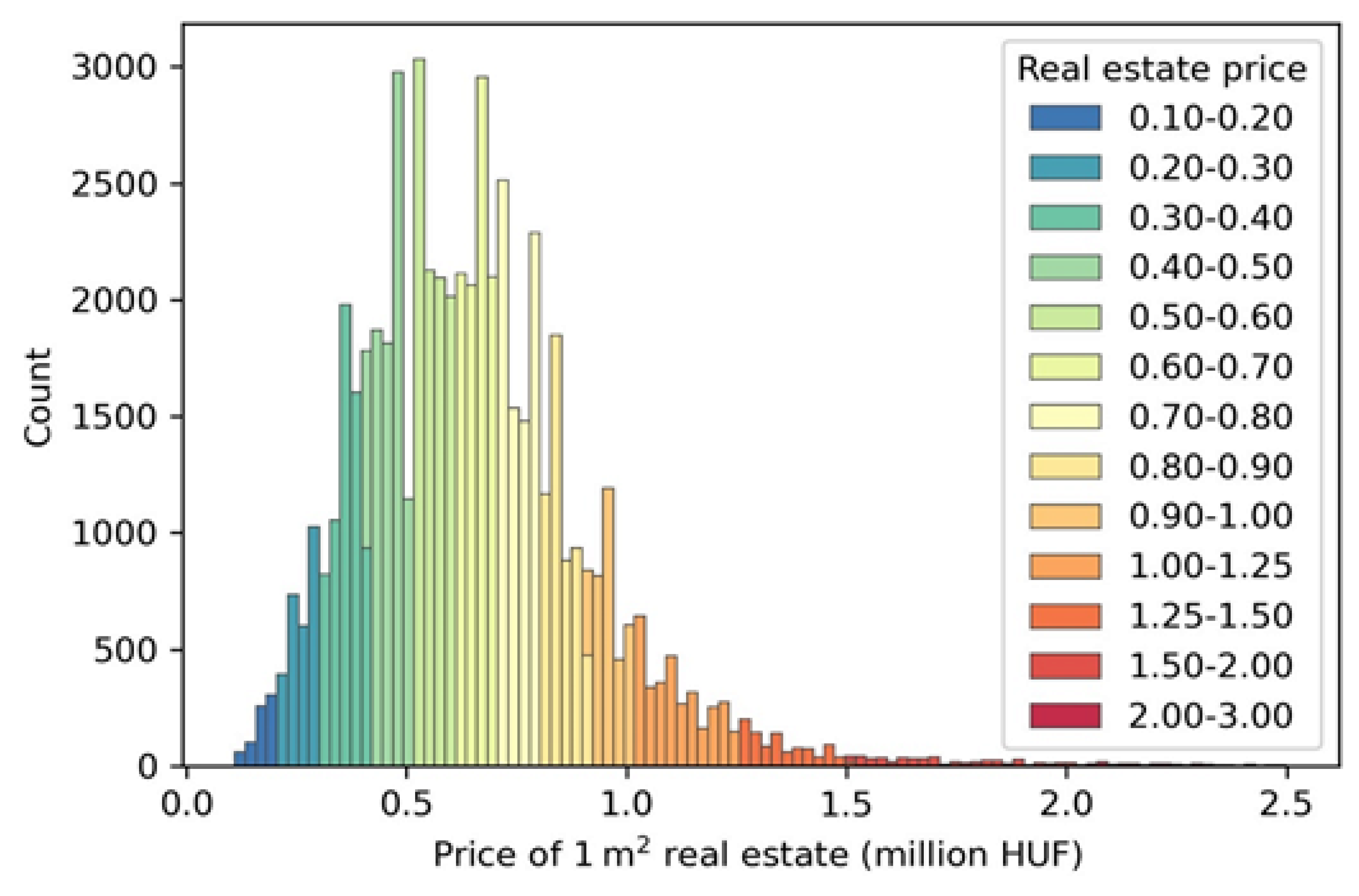
3.1. Statistical Results
3.2. Training Results
3.3. Testing Results
3.4. The Interactions of Variables on the Testing Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nanda, A. Residential Real Estate Urban & Regional Economic Analysis; Taylor and Francis: London, UK, 2019; pp. 66–80. [Google Scholar] [CrossRef]
- Rhoads, D.; Serrano, I.; Borge-Holthoefer, J.; Solé-Ribalta, A. Measuring and Mitigating Behavioural Segregation Using Call Detail Records. EPJ Data Sci. 2020, 9, 1–17. [Google Scholar] [CrossRef]
- Zhang, D.; Cao, J.; Feygin, S.; Tang, D.; Shen, Z.J.M.; Pozdnoukhov, A. Connected Population Synthesis for Transportation Simulation. Transp. Res. Part. C Emerg. Technol. 2019, 103, 1–16. [Google Scholar] [CrossRef]
- Hu, Y.; Hu, Y. Identification of Urban Functional Areas Based on POI Data: A Case Study of the Guangzhou Economic and Technological Development Zone. Sustainability 2019, 11, 1385. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Huang, Z.; Wu, F.; Zhu, M.; Guan, H.; Maciejewski, R. VAUD: A Visual Analysis Approach for Exploring Spatio-Temporal Urban Data. IEEE Trans. Vis. Comput. Graph. 2017, 24, 2636–2648. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Zhang, F.; Peng, W.; Gao, S.; Rao, J.; Duarte, F.; Ratti, C. Understanding House Price Appreciation Using Multi-Source Big Geo-Data and Machine Learning. Land Use Policy 2020, 8, 104919. [Google Scholar] [CrossRef]
- Wilson, E.; Whittaker, R.J. Real-Time Traffic Monitoring Using Mobile Phone Data. Mol. Cell Biol. 2005, 13, 1315–1322. [Google Scholar]
- Vidović, K.; Šoštarić, M.; Mandžuka, S.; Kos, G. Model for Estimating Urban Mobility Based on the Records of User Activities in Public Mobile Networks. Sustainability 2020, 12, 838. [Google Scholar] [CrossRef] [Green Version]
- Marshall, A.M.; Miller, P. CaseNote: Mobile Phone Call Data Obfuscation & Techniques for Call Correlation. Digit. Investig. 2019, 29, 82–90. [Google Scholar] [CrossRef]
- Wang, G.; Wu, N. A Comparative Study on Contract Recommendation Model: Using Macao Mobile Phone Datasets. IEEE Access 2020, 8, 39747–39757. [Google Scholar] [CrossRef]
- Anda, C.; Erath, A.; Fourie, P.J. Transport Modelling in the Age of Big Data. Int. J. Urban Sci. 2017, 21, 19–42. [Google Scholar] [CrossRef]
- Kang, H.; Jwa, J. Development of Android Based Smart Tourism Application Based on Tourism Bigdata Analytics. J. Eng. Appl. Sci. 2018, 13, 1164–1169. [Google Scholar] [CrossRef]
- Sumathi, V.P.; Kousalya, K.; Vanitha, V.; Cynthia, J. Crowd Estimation at a Social Event Using Call Data Records. Int. J. Bus. Inf. Syst. 2018, 28, 246–261. [Google Scholar] [CrossRef]
- Grigorash, A.; O’Neill, S.; Bond, R.B.; Ramsey, C.; Armour, C.; Mulvenna, M.D. Predicting Caller Type From a Mental Health and Well-Being Helpline: Analysis of Call Log Data. JMIR Ment. Health 2018, 5, 47. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Zhu, T.; Wan, X.; Wang, X. Identifying Significant Places Using Multi-Day Call Detail Records. In Proceedings of the 2014 IEEE 26th International Conference on Tools with Artificial Intelligence, Limassol, Cyprus, 10–12 November 2014; pp. 360–366. [Google Scholar] [CrossRef]
- Chen, N.C.; Xie, W.; Welsch, R.E.; Larson, K.; Xie, J. Comprehensive Predictions of Tourists’ Next Visit Location Based on Call Detail Records Using Machine Learning and Deep Learning Methods. In Proceedings of the 2017 IEEE 6th International Congress on Big Data (BigData Congress), Honolulu, HI, USA, 25–30 June 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Singh, A.V.; Juyal, V.; Saggar, R. Trust Based Intelligent Routing Algorithm for Delay Tolerant Network Using Artificial Neural Network. Wirel. Netw. 2017, 23, 693–702. [Google Scholar] [CrossRef]
- Fernando, M.L. Spatio Temporal Forecasting of Dengue Outbreaks Using Machine Learning. Ph.D. Thesis, University of Moratuwa, Moratuwa, Sri Lanka, 2019. [Google Scholar]
- Nair, S.C.; Elayidom, M.S.; Gopalan, S. Call Detail Record-Based Traffic Density Analysis Using Global K-Means Clustering. Int. J. Intell. Enterp. 2020, 7, 176. [Google Scholar] [CrossRef]
- Zhang, G.; Rui, X.; Poslad, S.; Song, X.; Fan, Y.; Wu, B. A Method for the Estimation of Finely-Grained Temporal Spatial Human Population Density Distributions Based on Cell Phone Call Detail Records. Remote Sens. 2020, 12, 2572. [Google Scholar] [CrossRef]
- Xu, Y.; Shaw, S.-L.; Zhao, Z.; Yin, L.; Fang, Z.; Li, Q. Understanding Aggregate Human Mobility Patterns Using Passive Mobile Phone Location Data: A Home-Based Approach. Transportation 2015, 42, 625–646. [Google Scholar] [CrossRef]
- Blumenstock, J.; Cadamuro, G.; On, R. Predicting Poverty and Wealth from Mobile Phone Metadata. Science 2015, 350, 1073–1076. [Google Scholar] [CrossRef] [Green Version]
- Batty, M.; Axhausen, K.W.; Giannotti, F.; Pozdnoukhov, A.; Bazzani, A.; Wachowicz, M.; Ouzounis, G.; Portugali, Y. Smart Cities of the Future. Eur. Phys. J. Spéc. Top. 2012, 214, 481–518. [Google Scholar] [CrossRef] [Green Version]
- Calabrese, F.; Colonna, M.; Lovisolo, P.; Parata, D.; Ratti, C. Real-Time Urban Monitoring Using Cell Phones: A Case Study in Rome. IEEE Trans. Intell. Transp. Syst. 2010, 12, 141–151. [Google Scholar] [CrossRef]
- Csáji, B.C.; Browet, A.; Traag, V.A.; Delvenne, J.-C.; Huens, E.; Van Dooren, P.; Smoreda, Z.; Blondel, V.D. Exploring the Mobility of Mobile Phone Users. Phys. A Stat. Mech. Appl. 2013, 392, 1459–1473. [Google Scholar] [CrossRef] [Green Version]
- Pappalardo, L.; Simini, F.; Rinzivillo, S.; Pedreschi, D.; Giannotti, F.; Barabási, A.-L. Returners and Explorers Dichotomy in Human Mobility. Nat. Commun. 2015, 6, 8166. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Z.; Ling, X.; Wang, P.; Zhang, F.; Mao, Y.; Lin, T.; Wang, F.-Y. Modeling Real-Time Human Mobility Based on Mobile Phone and Transportation Data Fusion. Transp. Res. Part. C Emerg. Technol. 2018, 96, 251–269. [Google Scholar] [CrossRef]
- Xu, Y.; Belyi, A.; Bojic, I.; Ratti, C. Human Mobility and Socioeconomic Status: Analysis of Singapore and Boston. Comput. Environ. Urban Syst. 2018, 72, 51–67. [Google Scholar] [CrossRef]
- Song, C.; Koren, T.; Wang, P.; Barabási, A.-L. Modelling the Scaling Properties of Human Mobility. Nat. Phys. 2010, 6, 818–823. [Google Scholar] [CrossRef] [Green Version]
- Kostic, Z.; Jevremović, A. What Image Features Boost Housing Market Predictions? IEEE Trans. Multimed. 2020, 22, 1904–1916. [Google Scholar] [CrossRef]
- Cottineau, C.; Vanhoof, M. Mobile Phone Indicators and Their Relation to the Socioeconomic Organisation of Cities. ISPRS Int. J. Geo-Inf. 2019, 8, 19. [Google Scholar] [CrossRef] [Green Version]
- Parija, S.R.; Sahu, P.K.; Singh, S.S. Mobility Pattern of Individual User in Dynamic Mobile Phone Network Using Call Data Record. Int. J. Wirel. Mob. Comput. 2019, 17, 23–35. [Google Scholar] [CrossRef]
- Vanhoof, M.; Schoors, W.; Van Rompaey, A.; Plötz, T.; Smoreda, Z. Comparing Regional Patterns of Individual Movement Using Corrected Mobility Entropy. J. Urban Technol. 2018, 25, 27–61. [Google Scholar] [CrossRef]
- National Media and Infocommunications Authority, Hungary. A Nemzeti Média- és Hírközlési Hatóság Mobilpiaci Jelentése 2015. IV–2019. II. Negyedév; Technical Report; National Media and Infocommunications Authority: Budapest, Hungary, 2019. [Google Scholar]
- Gonzalez, M.C.; Hidalgo, C.A.; Barabasi, A.L. Understanding Individual Human Mobility Patterns. Nature 2008, 453, 779–782. [Google Scholar] [CrossRef]
- Pappalardo, L.; Vanhoof, M.; Gabrielli, L.; Smoreda, Z.; Pedreschi, D.; Giannotti, F. An Analytical Framework to Nowcast Well-Being Using Mobile Phone Data. Int. J. Data Sci. Anal. 2016, 2, 75–92. [Google Scholar] [CrossRef] [Green Version]
- Tanemura, M.; Ogawa, T.; Ogita, N. A New Algorithm for Three-Dimensional Voronoi Tessellation. J. Comput. Phys. 1983, 51, 191–207. [Google Scholar] [CrossRef]
- Jain, S.; Shukla, S.; Wadhvani, R. Dynamic selection of normalization techniques using data complexity measures. Expert Syst. Appl. 2018, 106, 252–262. [Google Scholar] [CrossRef]
- Ruck, D.W. Feature selection using a multilayer perceptron. J. Neural Netw. Comput. 1990, 2, 40–48. [Google Scholar]
- Chatterjee, S. Particle swarm optimization trained neural network for structural failure prediction of multistoried RC buildings. Neural Comput. Appl. 2017, 28, 2005–2016. [Google Scholar] [CrossRef]
- Gardner, M.W.; Dorling, S.R. Artificial neural networks (the multilayer perceptron)—A review of applications in the atmospheric sciences. Atmos. Environ. 1998, 32, 2627–2636. [Google Scholar] [CrossRef]
- Ramchoun, H.; Idrissi, M.A.J.; Ghanou, Y.; Ettaouil, M. Multilayer Perceptron: Architecture Optimization and Training. IJIMAI 2016, 4, 26–30. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Ince, T.; Yildirim, A.; Gabbouj, M. Evolutionary artificial neural networks by multi-dimensional particle swarm optimization. Neural Netw. 2009, 22, 1448–1462. [Google Scholar] [CrossRef] [Green Version]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization. Swarm Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Verma, J.P. Data Analysis in Management with SPSS Software; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]







| Sum of Squares | Mean Square | F | Sig. | |||
|---|---|---|---|---|---|---|
| dweller entropy × estate price | Between Groups | (Combined) | 83.073 | 0.044 | 1.558 | 0.000 |
| Linearity | 0.871 | 0.871 | 30.899 | 0.000 | ||
| Deviation from Linearity | 82.201 | 0.043 | 1.542 | 0.000 | ||
| dweller gyration × real estate price | Between Groups | (Combined) | 98.941 | 2256 | 0.044 | 0.000 |
| Linearity | 6.146 | 1 | 6.146 | 0.000 | ||
| Deviation from Linearity | 92.795 | 2255 | 0.041 | 0.000 | ||
| Worker entropy × real estate price | Between Groups | (Combined) | 86.504 | 1867 | 0.046 | 0.000 |
| Linearity | 4.592 | 1 | 4.592 | 0.000 | ||
| Deviation from Linearity | 81.912 | 1866 | 0.044 | 0.000 | ||
| Worker gyration × real estate price | Between Groups | (Combined) | 98.704 | 2262 | 0.044 | 0.000 |
| Linearity | 0.156 | 1 | 0.156 | 0.000 | ||
| Deviation from Linearity | 98.548 | 2261 | 0.044 | 0.000 | ||
| Dwellers work distance × real estate price | Between Groups | (Combined) | 98.168 | 2234 | 0.044 | 0.000 |
| Linearity | 2.306 | 1 | 2.306 | 0.000 | ||
| Deviation from Linearity | 95.862 | 2233 | 0.043 | 0.000 | ||
| Workers home distance × real estate price | Between Groups | (Combined) | 99.112 | 2261 | 0.044 | 0.000 |
| Linearity | 3.506 | 1 | 3.506 | 0.000 | ||
| Deviation from Linearity | 95.605 | 2260 | 0.042 | 0.000 | ||
| Performance Index | Neuron Number | 10 | 12 | 14 | Pop. size |
|---|---|---|---|---|---|
| MSE | MLP | 0.0419 | 0.0427 | 0.0424 | - |
| MLP-PSO | 0.0301 | 0.03 | 0.0407 | 100 | |
| 0.042 | 0.0397 | 0.029 | 150 | ||
| 0.0406 | 0.0391 | 0.0395 | 200 | ||
| SI | MLP | −0.15585 | −0.15818 | −0.15873 | - |
| MLP-PSO | −0.11380 | −0.11021 | −0.15175 | 100 | |
| −0.15610 | −0.14916 | −0.10855 | 150 | ||
| −0.15234 | −0.14580 | −0.14714 | 200 | ||
| WI | MLP | 0.70706 | 0.70372 | 0.71219 | - |
| MLP-PSO | 0.82790 | 0.82585 | 0.71817 | 100 | |
| 0.71428 | 0.72410 | 0.83918 | 150 | ||
| 0.72033 | 0.74003 | 0.73372 | 200 |
| Model | MSE | SI | WI | |
|---|---|---|---|---|
| Model 1 | MLP 10 | 0.0403 | −0.14857 | 0.70780 |
| Model 2 | MLP-PSO 10-100 | 0.0393 | −0.14723 | 0.77701 |
| Model 3 | MLP-PSO 12-100 | 0.0411 | −0.17166 | 0.78043 |
| Model 4 | MLP-PSO 14-150 | 0.0414 | −0.15900 | 0.76584 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pinter, G.; Mosavi, A.; Felde, I. Artificial Intelligence for Modeling Real Estate Price Using Call Detail Records and Hybrid Machine Learning Approach. Entropy 2020, 22, 1421. https://doi.org/10.3390/e22121421
Pinter G, Mosavi A, Felde I. Artificial Intelligence for Modeling Real Estate Price Using Call Detail Records and Hybrid Machine Learning Approach. Entropy. 2020; 22(12):1421. https://doi.org/10.3390/e22121421
Chicago/Turabian StylePinter, Gergo, Amir Mosavi, and Imre Felde. 2020. "Artificial Intelligence for Modeling Real Estate Price Using Call Detail Records and Hybrid Machine Learning Approach" Entropy 22, no. 12: 1421. https://doi.org/10.3390/e22121421
APA StylePinter, G., Mosavi, A., & Felde, I. (2020). Artificial Intelligence for Modeling Real Estate Price Using Call Detail Records and Hybrid Machine Learning Approach. Entropy, 22(12), 1421. https://doi.org/10.3390/e22121421







