1. Introduction
The ideas of networked economy, pervasive transmission channels, systemic risk and complexity have become increasingly important after the 2008 financial crisis, but nowadays they are major concern on the impact of global trade tensions. Over the last decades, international fragmentation of production has made a huge transformation in geography and dynamics of international trade. Such fragmentation of production activities has given rise to the global value chains (GVCs) and greatly contributed to reinforce the structural interdependence worldwide. The global production networks are very complex, with flows of value-added representing a final outcome of the complex linkages that exist between firms in different industries and countries over time. The evaluation of these linkages calls for developing new tools that go well beyond the appraisal of bilateral gross trade flows. The network analysis and related metrics are extremely important in assessing the complexity of the whole structure of interactions (direct and indirect linkages) in the world economy, whilst the current research is still in its infancy.
So far, various macroeconomic models have been developed, ranging from dynamic stochastic general equilibrium modeling to agent-based macroeconomic models. The former assumes, in a standard setting, an economy that is populated by both an infinitely-lived representative household and a representative firm, with homogeneous production technology that is hit by exogenous shocks. The latter, on the other hand, considers an economy populated by heterogeneous agents, whose far from equilibrium interactions continuously change the structure of the system. Most of the models are, to some extent, descended from the Leontief’s work on input–output tables [
1], in which firm/agent interactions are mainly characterized by the global production networks. The latter are typically described with the so-called multi-regional input–output (MRIO) models that combine, in a coherent framework, national input–output and trade flow tables. In addition to tracking GVCs, together with other methodologies, such as life cycle assessment and material flow analysis, MRIO models have been used for sustainability analysis addressing a wide range of policy and research questions regarding the impacts of global production networks [
2]. There are several independently constructed global MRIO databases. In this paper, all theoretical results are accompanied with numerical computations of the World Input–Output Database (WIOD) [
3].
Basically, our approach was motivated by the recent observations in two strands of theoretical and empirical literature: shock propagation in economic networks and value chain positioning. The production network can work as a channel for propagating shocks throughout the economy. The possibility that substantial aggregate fluctuations may originate from microeconomic shocks has long been abandoned in the literature (see for example [
4]). This is mainly due to the ‘diversification argument’, which states that, in an economy consisting of
n industries hit by independent shocks, aggregate fluctuations would have a magnitude that is roughly proportional to
, a minor effect at high levels of disaggregation. This argument, however, disregards the input–output linkages between different firms and industries operating as a propagation channel of idiosyncratic microeconomic shocks throughout the economy [
5,
6,
7,
8,
9,
10]. The other main question of interest is the representation of network-originated macro fluctuations in terms of the economy’s structural parameters. In line with the key observations of [
5,
11], different roles various sectors play as input suppliers to others may generate sizable aggregate volatility when compared against the standard diversification argument rate. Microeconomic shocks may propagate over the network, but if propagated symmetrically, they would average out, and thus, would have minimal aggregate effects (hence the diversification argument remains applicable). The diversification argument would not hold, however, if intersectoral input–output linkages do not display such symmetries. Put differently, when sectors are highly asymmetric as input suppliers, even with a large number of industries, shocks to sectors that are more important suppliers propagate strongly to the rest of the economy producing significant aggregate fluctuations. Similarly, an industry will take a more ‘central’ position in the network if it plays a more important role as an input supplier to other central industries, and thus, it will be more influential in determining the aggregate output (see for example the Bonacich centrality). This statement goes in line with the intuition that productivity shocks to an industry with more direct or indirect downstream customers should have sizable aggregate effects.
The second strand of the literature pays particular attention to quantifying the relative production line position of industries/countries (or country—industry pairs) in (global) value chains. By dramatically changing the organization of world production, the rise of GVCs has laid in focus the specialization of countries within the global value chains. In point of fact, if shocks propagate downstream (to customer industries, supply-side shocks) or upstream (to input-supplying industries, demand-side shocks), the economic condition of a certain industry/country/country—industry pair is largely dependent on its relative position along the global output supply chain and the global input demand chain. The positions are usually measured relative to final consumers and primary inputs as downstream and upstream ends of value chains. The “upstreamness from final consumption” and “downstreamness from primary factors” are two numerical estimates (based on the length of output supply/input demand chains, respectively) that measure the country‘s/industry‘s/country—industry pair‘s position in global production processes [
12,
13,
14,
15]. However, two limitations, as argued by [
16] may possibly reduce the reliability of ‘upstreamness’ and ‘downstreamness’: first, they all begin with an industry’s gross output, whilst the production chain should begin with the industry’s primary inputs (or the sources of value added). Second, these measures do not imply each other and might suggest inconsistent positions for the same country—industry pairs. Besides, there is hardly any systematic empirical research on the firms’ decisive factors about controlling different segments of their production processes. A rare exemption is the study of [
17] who try to build firm-level measures of upstreamness of integrated and non-integrated inputs by combining detailed data on production activities of firms around the world with the standard input–output tables. Following this intuition, the most recent work of [
18] proposes a measure of the input rank to examine the organization of global supply networks at firm level. The supplier’s input rank persists (as an important predicting tool of the firm’s decision to integrate), even “after controlling for the relative positions on upstreamness/downstreamness segments” [
18].
Our work concentrates on absorbing Markov chains and their applications on ever growing topic of economic networks. The first theoretical linkage between Markov chain and Leontief input–output models was derived by Solow in 1952 [
19]. In spite of the great variety of mathematical properties, so far, however, world economic networks have not been fully examined with Markov chain formalism. An exemption is the recent attempt of [
20] who try to examine the evolution of world economic network by a series of finite state Markov chains and the work of [
21], where the random walk Markov chain approach is employed to detect and evaluate the importance of communities in the world input–output network. Unlike our approach, both papers examine a closed input–output system that can be translated naturally into a regular Markov chain with no absorbing states. The resource-specific network approach of [
22] that is based on an absorbing Markov chain and intended for use with an open input–output model is probably more closely related to our work. Yet, the paper describes the relationship between the absorbing Markov chain and input–output model with a focus on the Ghosh matrix and treats only the consumption goods as absorbing states [
22]. Moreover, the authors themselves emphasize that absorbing Markov chain analysis should be applied to more elaborated models (or “a model of the world economy is required, because material cycles are global in scope” [
22]) than the input–output framework implemented in their illustrative numerical example.
Given the importance of the distinctive features of output supply chain and input demand chain, in this paper, using the most recent world input–output database, we propose and investigated some novel properties of two (input and output) discrete-time absorbing Markov chains and set them against the prevailing approaches of output upstreamness and input downstreamness. Our main contribution to existing literature lies in the introduction of three newly established theorems and several related metrics characterizing the positions, length of chains and structural interdependence of the world economy (especially in regard to propagation and effects of economic shocks). Given the importance for policy makers to identify the most appropriate targets (industries) for economic stimulation purposes, we first provide a mathematical framework for ordering (ranking) the country—industry pairs according to values of ‘upstreamness’ and ‘downstreamness’ (as indicators pointing to the prominence or ‘keyness’ of a certain industry). Further, we propose a random endogenous variable pointing to the number of intermediate sales/purchases before absorption (final demand or primary inputs/sources of value added). The variance of this variable can serve as a useful guide for policy creators when determining the “optimal level of fragmentation” and hence, developing better models of production. The proof of our second theorem points to exactly the same quasi-stationary product distribution of both chains, that is, the product distribution does not depend on the type of the network (world input or world output network). This rather puzzling finding is probably at odds with the intuition of country’s positioning in specific segments of GVCs in line with their comparative advantage. Finally, the proposed global metrics (global domestic value-added, global import-export value-added, global domestic final use and global import-export final use) and our measures about the probability distribution of value added (global value added matrix) or final output (global final demand matrix) across countries provide some new insights for the analysis of trade in value added, or novel proxies of participation in global value chains than those currently available (e.g., backward and forward GVC participation).
The rest of the paper is organized as follows.
Section 2 describes context of the paper and data collection instruments and outlines the major analysis methods.
Section 3 presents the main findings and discusses results with reference to preceding research, as well as to their practical and policy implications. The last section provides the main conclusions of the research.
2. Materials and Methods
2.1. World Input–Output Database
The analyses performed here are based on data from 2016 release of the World Input–Output Database (WIOD). The latter contains annual time-series of world input–output tables. A world input–output table (WIOT) can be viewed as a set of national input–output tables that are linked together through detailed bilateral international trade statistics. In short, WIOT provides a comprehensive summary of all international transactions between industries and final consumers. The columns in the WIOT contain information about production processes. When expressed as ratios to gross output, the cells in a column deliver information on the shares of inputs in total costs. Such a vector of cost shares in gross output is commonly referred to as a production technology. Products can be purchased by final users, or final demand expenditures (households consumption, government consumption, gross fixed capital formation and change in inventories) or integrated into other goods and services (intermediates). The distribution of the output of industries over user categories is indicated in the rows of the table. An important accounting identity in the WIOT is that gross output of each industry (given in the last element of each column) is equal to the sum of all uses of the output from that industry (given in the last element of each row).
The 2016 release covers forty-three countries, including 28 EU member states and 15 other major economies, for the period from 2000 to 2014. The countries are selected on the basis of both data quality and aspirations to include a major part of the world economy. These countries together cover more than 85% of the world GDP; a model was estimated for the remaining non-covered part of the world economy, or the ‘rest of the world’ region. The WIOD is structured according to the recent industry and product classification ISIC Rev. 4 (or equivalently NACE Rev. 2), with the underlying WIOTs covering 56 industries. Further information about the included countries and industries can be found in [
3,
23]. The dataset is available at
http://www.wiod.org/home.
As the data has more than two dimensions, it should be arranged as multidimensional arrays, which are often called tensors. The order of a tensor is the number of dimensions. Vectors (tensors of order one) are denoted by boldface lowercase letters, e.g., . Matrices (tensors of order two) are indicated by boldface capital letters, e.g., . Higher-order tensors (order three or higher) are symbolized by math calligraphy letters, e.g., . Scalars are designated by lowercase or uppercase letters, e.g., a or A. The i-th entry of a vector is denoted by , element of a matrix is denoted by or , element of a third-order tensor is indicated by or and element of a forth-order tensor is represented by () or ().
The WIOD includes detailed data for
J countries (indexed by
or
) and
S sectors (indexed by
r or
s) organized as two tensors: 4-order tensor
with entries
describing the intermediate purchases (input flows) by industry
s in country
from sector
r in country
; and 3-order tensor
with entries
denoting the final use in each country
of output originating from sector
r in country
. In addition, the WIOD includes matrices
,
and
, uniquely determined by the tensors
and
. The entries of these matrices are given as follows:
where
represents the value of gross output originating from sector
r in country
; the element
stands for the value of output from sector
r in country
intended for final consumers worldwide;
indicates the country’s
value-added employed in the production of an industry
s.
An N th-order tensor is an element of the tensor product of N vector spaces, each of which has its own coordinate system. Slices are two-dimensional sections of a tensor, defined by fixing all but two indices. Matricization, also known as unfolding or flattening, is the process of reordering the elements of an N-th order array into a matrix. For instance, a tensor can be arranged as a matrix or a matrix, and so on. It is also possible to vectorize a tensor; for example, tensor can be arranged as a 36 dimensional vector.
The world input–output table is obtained by unfolding the tensors and into and matrices respectively and by unfolding the matrices , and into vectors. Therefore, WIOT consists of the following elements:
matrix
with
and
and
, so that
element of the matrix describes the sales of intermediates from country—industry pair
i to country—industry pair
jn dimensional final demand vector with the i-th entry describing the sales from country—industry pair i to final users.
n dimensional gross-output vector where
n dimensional value-added vector where
2.2. World-Input and World-Output Networks
Consider a world economy with countries (economies): country-1, …, country-J and sectors (industries): sector-1, …, sector-S as a network of nodes in which each node represents a country—industry pair, where is the set of nodes and E is the set of edges to be defined shortly. Country–industry pairs are mapped to the nodes in V with , for and . Note that the nodes correspond to the country-1, the nodes are related to the country-2 and so on.
Let us first define and , so that the country—industry pairs are indexed by i and j, . Next, we associate two networks (world-input network and world-output network) with the vertex set . World-input network is represented by the adjacency input matrix for which . This normalization will be called “world-input” network, since, along the output supply chain, the country—industry pair i sells intermediate inputs to other country—industry pairs j’s in the world economy (the corresponding links are denoted by the input coefficients ).
For the world-output network, represents an adjacency output matrix of the second normalization with a typical element . This specification will be called (is known as) “world-output” network, since, along the input demand chain, the country—industry i buys intermediate inputs worldwide (the corresponding links from all country—industry pairs j’s to i are denoted by the output coefficients ). Note that the matrices and are similar, (, where is the diagonal matrix with elements of along its diagonal and zeros otherwise), share the same eigenvalues and their largest eigenvalue, , is real with .
The world production here is modeled linearly, that is
or
, where
and
. Let
and
be the Leontief-inverse matrix and Ghosh-inverse matrix, respectively. Then Equations (2) and (3) can be rewritten in a compact form as [
12,
13],
The two well-established metrics in input–output economics indicating the country—industry’s (weighted) average position in global value chains [
12,
13], the output upstreamness (or upstreamness) (OU),
, and the input downstreamness (or downstreamness) (ID),
, are defined as
and
, where
is a length-
n column vector whose entries are all 1. In the world-output network, the country—industry pairs with large values of
will produce complex and strong intermediate input demand edges with similar pairs (and vice versa for small values). In world-input network, on the other hand, the country—industry pairs with large
values will produce complex and strong intermediate output supply edges with similar pairs (and vice versa for small values).
2.3. Absorbing Markov Chains
We next turn to proposing alternative measures of the country—industry’s average position in global value chains. These measures can be estimated for both the output supply chain (hence relative to final consumption) and the input demand chain (thus relative to primary inputs). In order to understand the structure and organization of the world production, the input and output networks here are associated with two homogeneous discrete-time absorbing Markov chains, that is the
input-chain and the
output-chain. The state space of both chains is
, while the vertex set
V is considered as a set of transient states. For the world-input network, the absorbing state 0 represents final use of output. On the other hand, for world-output network, the absorbing state 0 represents primary factors of production (or sources of value added). If we define
the transition matrix
of the absorbing Markov input-chain reads
while the transition matrix
of the absorbing Markov output-chain is
where
T denotes transpose operator,
,
, and
is a length-
n column vector whose entries are all 0. Both matrices
and
are row stochastic. The column stochastic matrix
and row stochastic matrix
are the one-step transition probabilities of the (sub)Markov chain on
V and
and
are the one-step transition probabilities of absorption into the state 0.
Let us analyze the world input/output network with a Markov process (input-chain or output-chain). Assume that the process starts in state
at time 0, and let
(or 0) if the process is (or is not) in the state
j at time
t. Further, let
be a random variable representing the number of visits to state
j before absorption and
be another random variable—the time to absorption. To simplify notation, we write
for both matrices
and
and allow for
to be either
or
. From the standard theory of absorbing Markov chains, the following equations can be derived [
24]:
where
and
are expectation and variance of the random variable
X, respectively,
is a diagonal matrix,
,
is a length-
n column vector whose entries are all 1, and
.
When
, the transpose of the matrix defined with Equation (
11) coincides with the Leontief-inverse matrix
. For
, Equation (
11) reduces to the Ghosh-inverse matrix
. Moreover, from Equation (13), it follows that the expected number of steps before absorption is characterized with vectors (for the output and input networks)
and
. The metric
is a measure of distance of a country—industry pair from the final demand. Therefore,
describes “how far” (in expected number of steps) the production of a country—industry pair is from the final use (or “average production line position”). The second quantity
is a measure of distance of a country—industry pair from the primary factors of production (or sources of value-added). In another words,
measures “average distance from primary inputs suppliers”. Not all products, however, need to have their production split into multiple stages. Services, for example, are less inclined to vertical specialization when supplier is required to have a close contact with the consumer. The variance (of the number of steps before absorption) can help measure the volatility (or the risk) a country—industry pair assumes when determining the production chain lengths. It could therefore permit the country—industry pairs to develop better models of production by optimizing the level of fragmentation (that is a trade-off between higher transaction/coordination costs and lower costs of production).
For both absorbing Markov chains, the input-chain and the output-chain, the set of transient state V is irreducible. In terms of the world-input network, it means that for arbitrary two country—industry pairs i and j, even for those directly not connected (), the country—industry pair i, after finite number of jumps (hops/steps), sells intermediate inputs to the country—industry pair j. Similarly, irreducibility of the world-output network implies that an arbitrary country—industry pair, after finite number of purchases, buys intermediate inputs from all other country—industry pairs worldwide. However, since the Markov chains are absorbing, eventually, intermediate output sales and input purchases reach the absorbing state—the state from which further jumps are impossible (e.g., final consumers and primary factors or sources of value added).
Next, we consider two quasi-stationary distributions which are derived, roughly speaking, from observing only those realizations in which the time to absorption is long. Assume that the process starts in state
i with probability
. Let
. The probability that the process has been absorbed by time
t is given as
. Provided that the process is not absorbed at time
t, the conditional probability that the process is in state
j at time
t is computed as follows [
25]:
where
is the left dominant eigenvector of the matrix
,
is the second largest eigenvalue of the matrix
, and we have assumed, for simplicity only, that its multiplicity is 1. This vector is normalized,
, so it represents a quasi-stationary distribution of the absorbing Markov chain. In other words, the quasi-stationary distribution represents the proportion of time the process spends in a transient state, that is the number of times a particular country—industry pair contributes to its own production stages, or becomes an intermediate in its own supply/demand chains before absorption (given that the time to absorption is long). Note that the limit as
is
which is independent of the probability distribution
. Equation (
15) can be further generalized as [
25]:
where
is the right dominant eigenvector of the matrix
. This vector is normalized,
and therefore,
represents a quasi-stationary distribution of the absorbing Markov chain, which will be referred to as
product distribution. The left hand side of Equation (
16) converges to
as
and
. Note that
may be described as the distribution of the random variable at time
(
large), given that absorption has not yet taken place and will not take place for a long time. The product distribution is more relevant than
in the sense that the Equation (
15) is a “degenerate” case of the Equation (
16).
Further, we look attentively at the structure of the global production network from the “final use perspective” and “final value added perspective”. Here, we provide some basic definitions only for the final demand. A more detailed discussion for both perspectives will be presented in the
Section 3. Let
, where
and
be the probability that production from country—industry pair
i ends up as output purchased by the final users of country
. We arrange the elements
as
matrix
, which is called a
global final demand matrix. Let
and define
matrix
with elements
. In this case, Markov absorbing chain has
J absorbing states. The transition matrix, Equation (
10), now reads
where
is identity matrix and
zero matrix. A simple example for illustrating all quantities proposed in this subsection is provided in
Figure 1.
3. Results and Discussion
The organization of world production is characterized by the structure of the input/output networks. Let us rewrite the
matrix, Equation (
4), as follows:
where each
is
matrix. Diagonal block matrices in Equation (
19) represent domestic inter-industry transactions, while off-diagonal blocks show the inter-country flows of intermediates via exports and imports. The adjacency matrices
and
are also rearranged in this way and their mean values are shown in
Figure 2. The latter shows a growing fragmentation of production across countries worldwide. From 2000 onwards, the global production networks became more complex and increasingly interconnected as a result of massively increased trade in intermediates (goods or services) among countries, both as buyers of foreign intermediate inputs (off-diagonal blocks of matrix
) or sellers of intermediate products to third countries for further processing and export (off-diagonal blocks of matrix
). It is noteworthy, however, that international fragmentation of production seems to have lost momentum in recent years, at least compared to 2000s, especially when it comes to forward GVC participation (many companies are probably less agile in responding to changing consumer demands). The consolidation of some value chains has been observed even during the 2008–2009 financial crisis, with some country—industry pairs switching back to domestic suppliers (slight increase in the mean values of the diagonal block in
Figure 2) in the context of difficult access to trade finance and risks connected with international suppliers. Nevertheless, the recent slowdown may also point to a number of potential structural shifts facing the world economy (with many companies deciding to reexamine their outsourcing and production strategies), which could dramatically change the configuration of global production landscape and determine the future of globalization in a systemic way.
In input–output analysis, as mentioned before, upstreamness (
) and downstreamness (
) are used as measures of the importance of a certain country—industry pair
i. In essence, larger
values are related to relatively higher level of upstreamness of the particular country—industry pair
i. The latter thus provides little to final consumers worldwide and instead sells disproportionately large share of its output (as intermediate inputs) to other producing industries in the world economy. Conversely, larger
values are related to relatively higher level of downstreamness of a certain country—industry pair
i. Clearly, the production process here relies disproportionately on intermediate inputs relative to the value-added from primary factors of production, and especially if purchases are made from those country—industry pairs which themselves use intermediate inputs intensively. That is, other things being equal, country—industry pairs with large
or
values are being more proper targets for economic stimulation because they will bring much greater benefits to the entire world economy (by extending more of its resources to other country—industry pars in the former case, or by triggering other country—industry pairs to increase their outputs in the latter). It should also be noted, however, that a country—industry with higher levels of downstreamness exhibit greater productivity fluctuations, because “upstream supply-side shocks accumulate while propagating downstream” [
26]. Given the importance for policy makers, the next theorem provides mathematical framework for ordering (ranking) the country—industry pairs according to values of these measures (see
Appendix A for the proof of the theorem).
Theorem 1. The following approximations hold:where and are the left and the right dominant eigenvectors of the matrices and . Note that in Equations (
20) and (
21),
and
are vectors of out-degree and in-degree of the nodes of the output-network and input-network, respectively. Therefore, when
, it follows that the ordering (or the ranking) of the country—industry pairs depends only on the out-degree (in-degree) centrality, and thus, high-degree nodes are important, that is, the most important suppliers of value added in world GVCs (or the general-purpose country—industry pairs whose value added contained in intermediate inputs is sent to a wide range of country—industry pairs for further processing) and the country—industry pairs that import intermediates from many sources (or the most important recipients of foreign value added in global production networks). On the other hand, when
, the ordering (ranking) depends only on the right (left) dominant eigenvector of the matrix
(
). Therefore, in this case, it could happen that a low-degree country—industry pair has greater influence (i.e., it is a more relevant player in the global production networks) than the high-degree hub. Put differently, the centrality of a country—industry pair here is recurrently related to the pairs to which it is connected, that is a node’s position depends on the importance of its neighbors (a node eigenvector centrality).
Figure 3 shows the dominant eigenvalue of the world input/output network as well as the country dominant eigenvalues of the input/output networks of all countries versus time. The mean value of dominant eigenvalues of the input/output networks of all countries,
, is almost constant in time, while the dominant eigenvalue of the world input/output network,
, increases in time. Moreover,
Figure 4 depicts Spearman’s rank correlation between upstreamness (downstreamness) and the out-degree (in-degree) centrality and right dominant eigenvector of the adjacency matrix
(
) for the WIOD. In the limits
and
(that correspond to the limits
and
, respectively, see the
Appendix A), the orderings of
and
are perfectly matched with the ordering of the vectors from the right-hand side of the Equations (
20) and (
21), respectively. When
, the ordering of
and
is 95% correlated with the ordering of degree centrality and 80% with eigenvectors’ ordering.
Two random variables have been proposed in the previous section. Assume that the process starts in state
i. As already stated, the first random variable,
, represents the number of visits to state
j before absorption, while the second,
is the time to absorption. Expectation and variance of these random variables are provided by Equations (
11), (12), (13) and (14), respectively.
Figure 5 provides a visual display of summarizing a distribution of data, or comparative boxplots that can be used to compare the distributions of expectation and variance of the time to absorption for both the world-input and world-output networks. The most noticeable feature is that expectation, or expected number of steps before absorption, and variance of the number of steps before absorption for the output network (and the respective upstreamness) are generally higher than those for the input network (and the respective downstreamness). Put differently, the median and the upper quartile for the former sample are all above the corresponding values for the latter sample (the lower quartiles are roughly similar). The dispersion is also greater for the output network, that is the interquartile range, as revealed by the box lengths, is reasonably longer and so is the overall range of dataset (with or without ‘outliers’).
The next result unveils that both the input chain and the output chain have exactly the same quasi-stationary product distribution (for the proof of the theorem, see
Appendix B).
Theorem 2. The World input/output network is characterized with Note that although
and
, their products are equal to each other. Therefore, the product distribution does not depend on the type of network (input/output). In order to explain this result, we interpret the probability
as limiting conditional mean ratios. It can be shown that:
The left hand side of Equation (
23) is the expected proportion of time spent in the state
j before absorption. Since the transaction flows of intermediates coming from (or sold by) the pair
j (world input network) are, at the same time, equal to flows of intermediates purchased by the pair
j (world output network), the expected proportion of time spent in the state
j before absorption for the input network is equal to the expected proportion of time spent in the state
j before absorption for the output network. Moreover, note that
, see Equation (24), equals the number of visits to state
j up to time
t. Therefore, the expected proportion of time spent in the state
j before absorption is equal to
and does not depend on the type of the network (world input/world output network).
Figure 6 depicts the histograms of the product distribution
, the output upstreamness
and the input downstreamness
for the WIOD and the year 2014.
These findings would indicate that country—industry pairs appearing to be upstream according to their distance from final output users (output upstreamness) are at the same time downstream according to their distance from primary inputs (input downstreamness). Put differently, the country—industry pairs that sell a small share of their output to final consumers, or sell a large amount of intermediates to other pairs in the world economy (hence, appear to be upstream in GVCs) are also inclined to embody little value added relative to intermediate inputs in their production processes (hence, appear to be downstream in GVCs). This rather surprising fact runs counter to what might be imagined at a time of global production fragmentation. As global production networks rise in importance, one would expect that countries may possibly position themselves in those segments of GVCs in which they have comparative advantage. For example, countries with comparative advantage in basic parts or natural resources would specialize in early phases of production processes. Accordingly, they would exhibit a decrease in the share of gross output that is sold to final consumers and upward shift in the value added from primary inputs. On the contrary, countries with comparative advantage in production phases near to final assembly are expected to encounter a rise in the shares sold to final users and a decrease in their value added employed in the production processes. Our results, however, are surprisingly at variance with this prior intuition. Similar findings are documented in the study of [
27], although based on puzzling positive correlations (that increase over time) between the upstreamness and downstreamness. A full discussion of these developments is, however, beyond the scope of this paper.
The next result is actually a combination of the classical results in respect of the absorbing Markov chains [
24] and some new insights (for the proof, see
Appendix C).
Theorem 3. (i) The global final demand matrix can be computed assuch that is a row stochastic matrix. (iii) For an economy for which the row sums of are all equal to c, the input downstreamness is constant . If the row sums of are all equal to c, then the the output upstreamness is constant .
Note that the matrix
is the one-step transition matrix, while the vector (for a fixed
i)
is a probability distribution showing how the final output of country—industry pair
i is distributed among different countries. For a fixed industry
r we arrange the elements
in a
matrix,
which we call a
global final demand matrix of the industry r, showing the global patterns of final demand for any given industry. Similarly, if we write
and define
, it follows from Equation (
26) that the vector (for a fixed
i)
is the probability distribution showing how the value added of country—industry pair
i is distributed among different countries. Again, for a fixed industry
r we arrange the elements
in a
matrix,
which we call a
global value added matrix of the industry r, capturing the final impact after all stages of production have circulated throughout the world economy and showing the global patterns of value added for any given industry. This metric, which breaks down the distribution of gross trade flows along the sources and destinations of value added, provides a coherent answer to many important questions about the interconnections among countries, especially with regard to the aggregate impact and propagation of shocks. For example, the important role that particular countries play in international flows of value added raises the questions about the resilience of the world trading system if they suffer a large-scale economic shock. All of this has a major impact on forecasting the macroeconomic developments and on monetary policy decisions.
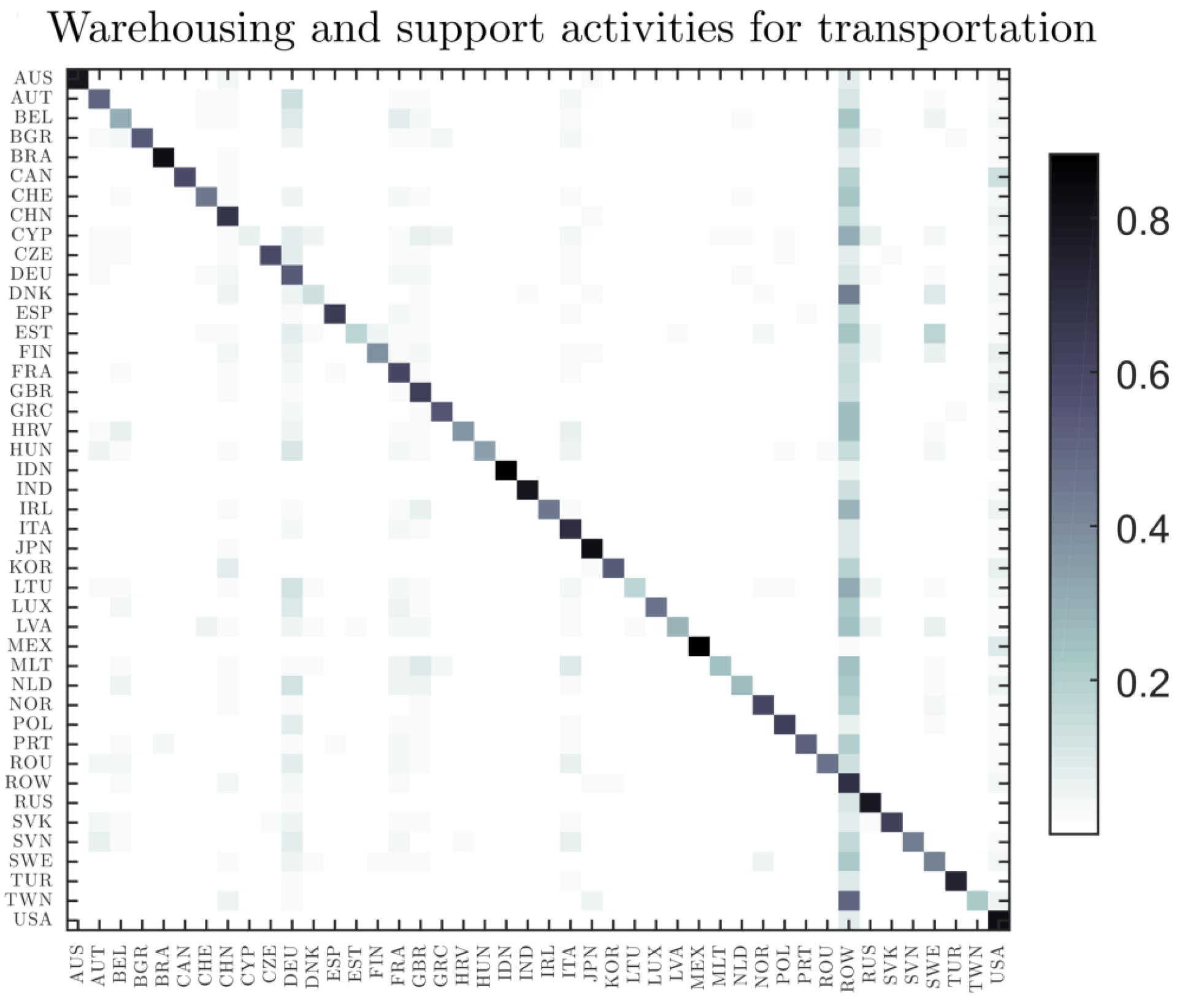
Figure 7 shows global demand matrix for the warehousing and support activities for transportation in 2014. Each row (a horizontal line) is a probability distribution: the
j element of the row
i shows the probability that a good/service produced in the country
i has been delivered to final consumers in country
j. On the other, the column
j (a vertical line) represents the final consumer buying patterns for a particular product (e.g., warehousing and support activities for transportation) in country
j.
Finally, the availability of global input–output matrices has paved the way to several methodological contributions on measures of trade in value added, or proxies of GVC participation (see [
28] for a review). In view of diagonal and off-diagonal blocks of our global value-added and global final demand matrices, the proposed metrics below provide some new insights or novel proxies for the analysis of global production chains:
The first indicator, which we call global domestic value-added (GDVA), refers to all domestic value-added flows within a given country—industry pair, irrespective of the number of steps along the chain (see Equation (
31)). Hence, the measure includes both, direct and indirect domestic value-added contents. The former denotes the income of primary inputs directly involved in production (one stage), while the latter encompasses both the domestic flows of intermediate goods and services across industries (hence, the magnitude only depends on the density of domestic intersectoral linkages) and domestic value-added that is re-imported in the economy of origin as a part of other intermediates (hence, the magnitude of value added depends on the density of intersectoral linkages between two or more countries). The second metric we call global import-export value-added (GIEVA) indicates the extent to which a country—industry pair is connected to global production networks for its foreign trade (see Equation (32)). Hence, this measure refers to inter-country transaction flows of intermediate products (goods and services) through exports and imports. The third indicator, or global domestic final use (GDFU), indicates the final use of domestic output by the country itself (see Equation (33)). The last indicator, which we call global import-export final use (GIEFU), refers to all imports and exports destined for final consumers worldwide (see Equation (34)). The evidence suggests that global production networks have provided a great impulse to globalization during the past decades (
Figure 8). After the marked growth during the early 2000s, international fragmentation of production has become a cornerstone of the global economy, with products effectively being “made in the world”. Growing fragmentation, with a short disruption during the 2008 financial crisis, is typically associated with more trade in intermediate inputs via exports and imports (an overall upward trend in GIEVA) and less domestic value added (noticeable decline in GDVA) (
Figure 8). Nevertheless, global production networks, at least compared to early 2000s, seem to have lost momentum during the last years (
Figure 8). In point of fact, the world production has been made more expensive since the economic crisis, mainly due to increasing trade costs and protectionism. Moreover, the recent steady state in GDFU and GIEFU (
Figure 8) points to a somewhat greater attractiveness of localized production and potentials for shortening the production chain lengths which means that individual parts and products would increasingly be manufactured in proximity to final users. It is clear that such dynamics in international fragmentation will promptly have impact on the world economy and probably give rise to a certain re-configuration of the global production networks.