Mutual Information Gain and Linear/Nonlinear Redundancy for Agent Learning, Sequence Analysis, and Modeling
Abstract
1. Introduction
2. Differential Entropy, Mutual Information, and Entropy Rate: Definitions and Notation
3. Agent Learning and Redundancy
4. Linear and Nonlinear Redundancy
5. Mutual Information Gain
5.1. Stationary and Gaussian
5.2. A Distribution Free Information Measure
6. Autoregressive Modeling
Example: Learning and Modeling an AR Sequence
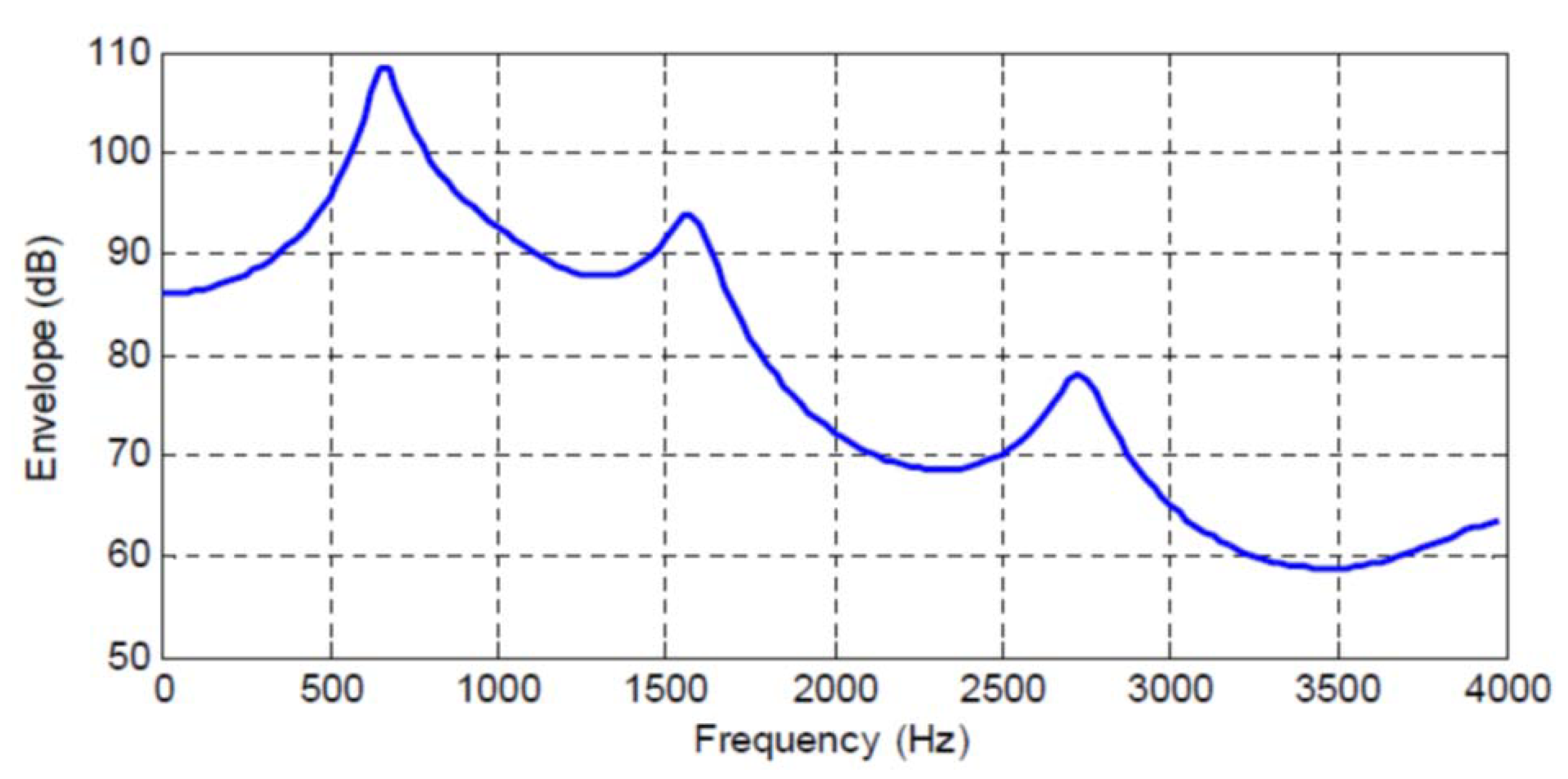
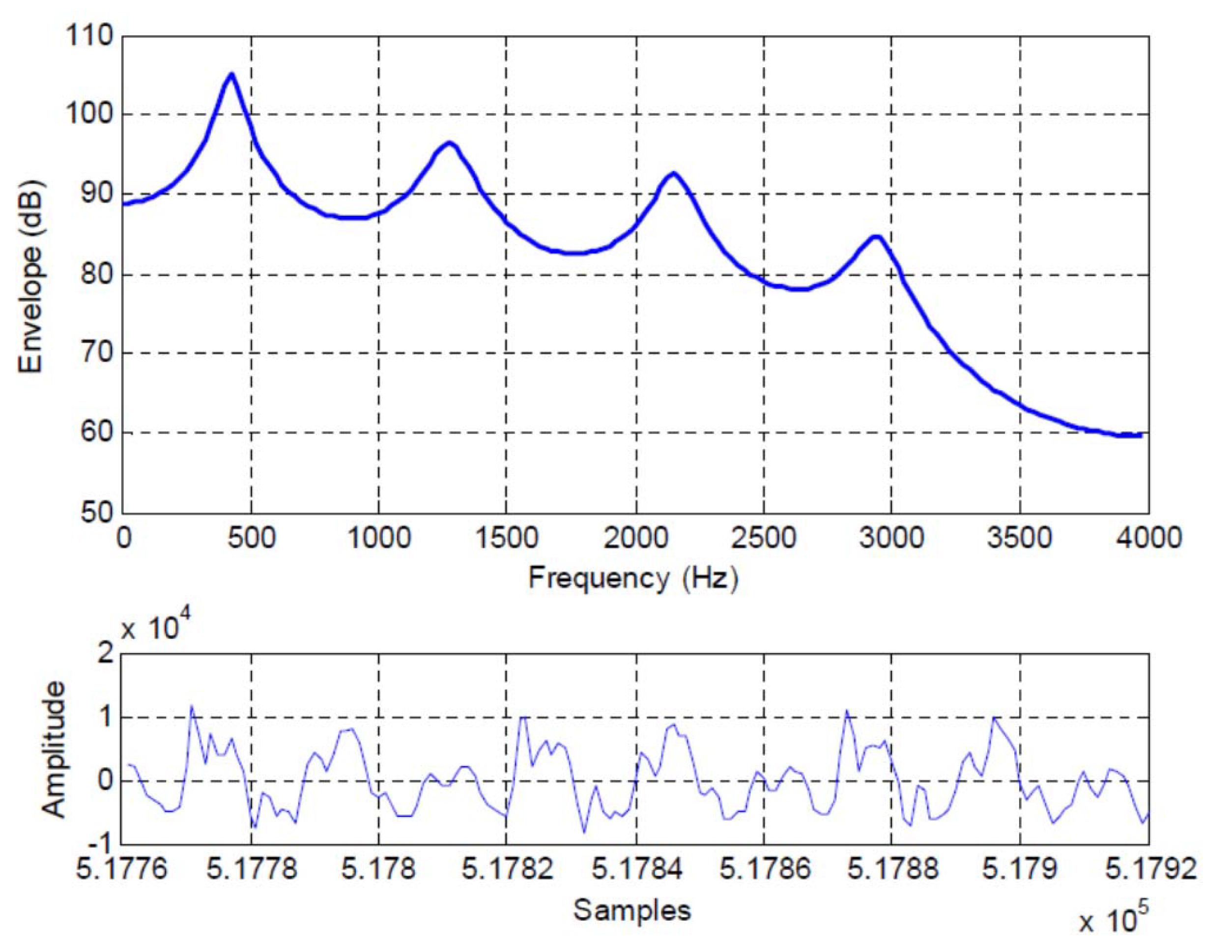
7. Speech Processing
7.1. AR Speech Model
7.2. Long Term Redundancy
8. Discussion and Conclusions
Funding
Conflicts of Interest
Abbreviations
| AR | Autoregressive |
| AR(M) | Autoregressive of order M |
| MMSPE | Minimum mean squared prediction error |
| Q | Entropy (rate) power |
| SPER | Signal to prediction error ratio |
Appendix A. Calculating the AR Model Coefficients
Correlation Matching
References
- Crutchfield, J.P.; Feldman, D.P. Synchronizing to the environment: Information-theoretic constraints on agent learning. Adv. Complex Syst. 2001, 4, 251–264. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; Feldman, D.P. Regularities unseen, randomness observed: Levels of entropy convergence. Chaos Interdiscip. J. Nonlinear Sci. 2003, 13, 25–54. [Google Scholar] [CrossRef] [PubMed]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Sayood, K. Introduction to Data Compression; Morgan Kaufmann Elsevier: Cambridge, MA, USA, 2012. [Google Scholar]
- Elias, P. A note on autocorrelation and entropy. Proc. Inst. Radio Eng. 1951, 39, 839. [Google Scholar]
- Ebeling, W. Prediction and entropy of nonlinear dynamical systems and symbolic sequences with LRO. Phys. D Nonlinear Phenom. 1997, 109, 42–52. [Google Scholar] [CrossRef]
- Makhoul, J.; Roucos, S.; Gish, H. Vector quantization in speech coding. Proc. IEEE 1985, 73, 1551–1588. [Google Scholar] [CrossRef]
- Rabiner, L.R.; Schafer, R.W. Digital Processing of Speech Signals; Prentice-Hall: Upper Saddle River, NJ, USA, 1979. [Google Scholar]
- Gibson, J.D.; Hu, J. Rate Distortion Bounds for Voice and Video; NOW: Hanover, MA, USA, 2014. [Google Scholar]
- Gibson, J. Speech Compression. Information 2016, 7, 32. [Google Scholar] [CrossRef]
- Markel, J.D.; Gray, A.H. Linear Prediction of Speech; Springer: Berlin, Germany, 1976; Volume 12. [Google Scholar]
- Gibson, J. Mutual Information, the Linear Prediction Model, and CELP Voice Codecs. Information 2019, 10, 179. [Google Scholar] [CrossRef]
- Gray, R.M. Linear Predictive Coding and the Internet Protocol; NOW: Hanover, MA, USA, 2010. [Google Scholar]
| M | |||
|---|---|---|---|
| 0 | 0 bits/symbol | 0 bits/symbol | |
| 1 | 0.842 | ||
| 2 | 1.952 | ||
| 3 | 2.044 | ||
| 4 | 2.348 | ||
| 5 | 2.367 | ||
| 6 | 2.432 | ||
| 7 | 2.501 | ||
| 8 | 2.501 | ||
| 9 | 2.621 | ||
| 10 | 2.647 | ||
| 0–10 | 2.647 | 2.647 |
| M | |||
|---|---|---|---|
| 0 | 0 bits/symbol | 0 bits/symbol | |
| 1 | 0.656 | ||
| 2 | 0.803 | ||
| 3 | 0.883 | ||
| 4 | 1.01 | ||
| 5 | 1.031 | ||
| 6 | 1.118 | ||
| 7 | 1.118 | ||
| 8 | 1.499 | ||
| 9 | 1.52 | ||
| 10 | 1.52 | ||
| 0–10 | 1.52 | 1.52 |
| Speech Frame No. | in dB | |
|---|---|---|
| 23 | bits/symbol | |
| 3314 | bits/symbol | |
| 87 | 5 | bits/symbol |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gibson, J.D. Mutual Information Gain and Linear/Nonlinear Redundancy for Agent Learning, Sequence Analysis, and Modeling. Entropy 2020, 22, 608. https://doi.org/10.3390/e22060608
Gibson JD. Mutual Information Gain and Linear/Nonlinear Redundancy for Agent Learning, Sequence Analysis, and Modeling. Entropy. 2020; 22(6):608. https://doi.org/10.3390/e22060608
Chicago/Turabian StyleGibson, Jerry D. 2020. "Mutual Information Gain and Linear/Nonlinear Redundancy for Agent Learning, Sequence Analysis, and Modeling" Entropy 22, no. 6: 608. https://doi.org/10.3390/e22060608
APA StyleGibson, J. D. (2020). Mutual Information Gain and Linear/Nonlinear Redundancy for Agent Learning, Sequence Analysis, and Modeling. Entropy, 22(6), 608. https://doi.org/10.3390/e22060608





