Rényi Entropy-Based Spectrum Sensing in Mobile Cognitive Radio Networks Using Software Defined Radio
Abstract
1. Introduction
2. Rényi Entropy Based Spectrum Sensing
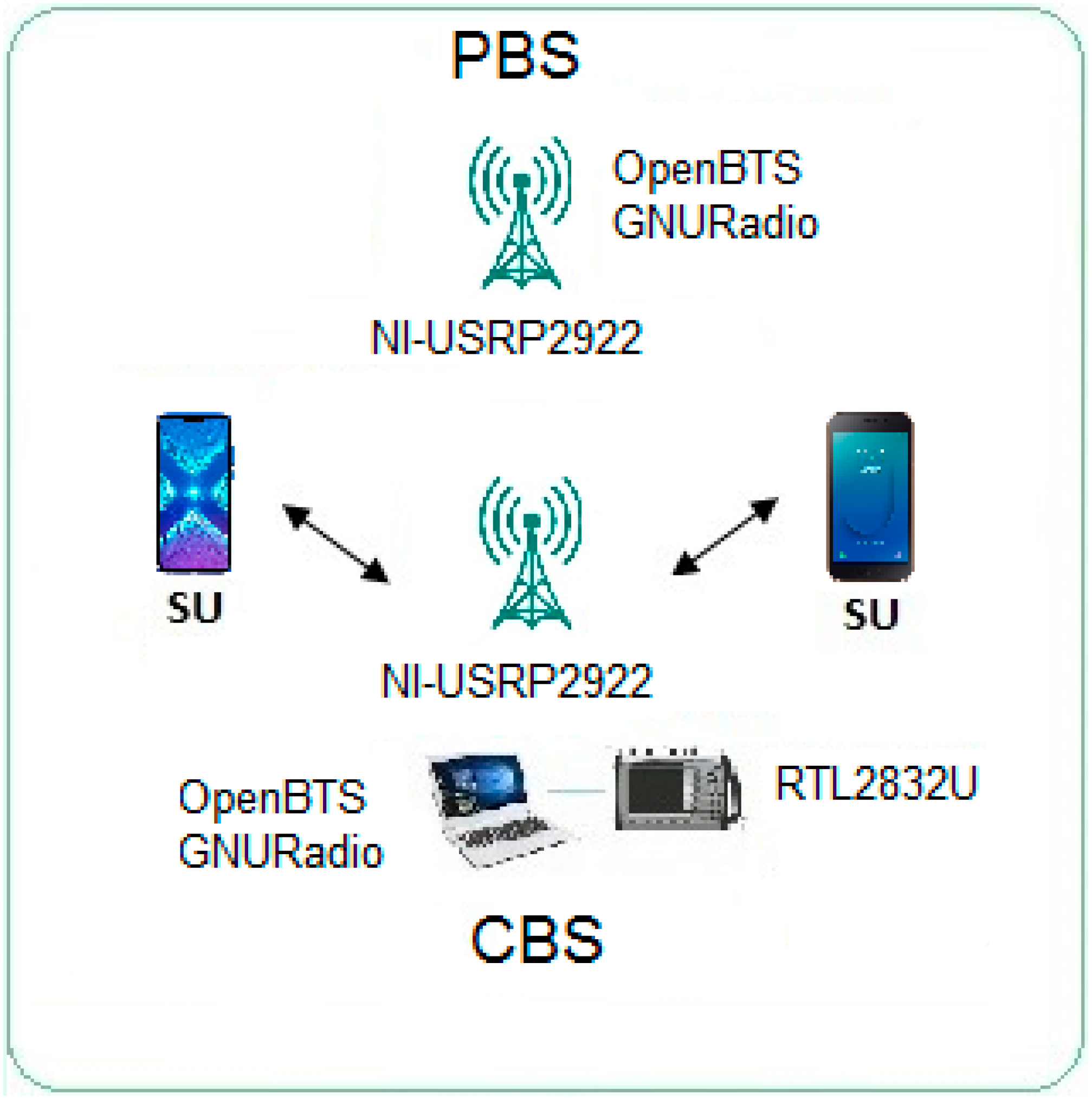
3. Software Defined Radio Testbed for Experiments
4. Results
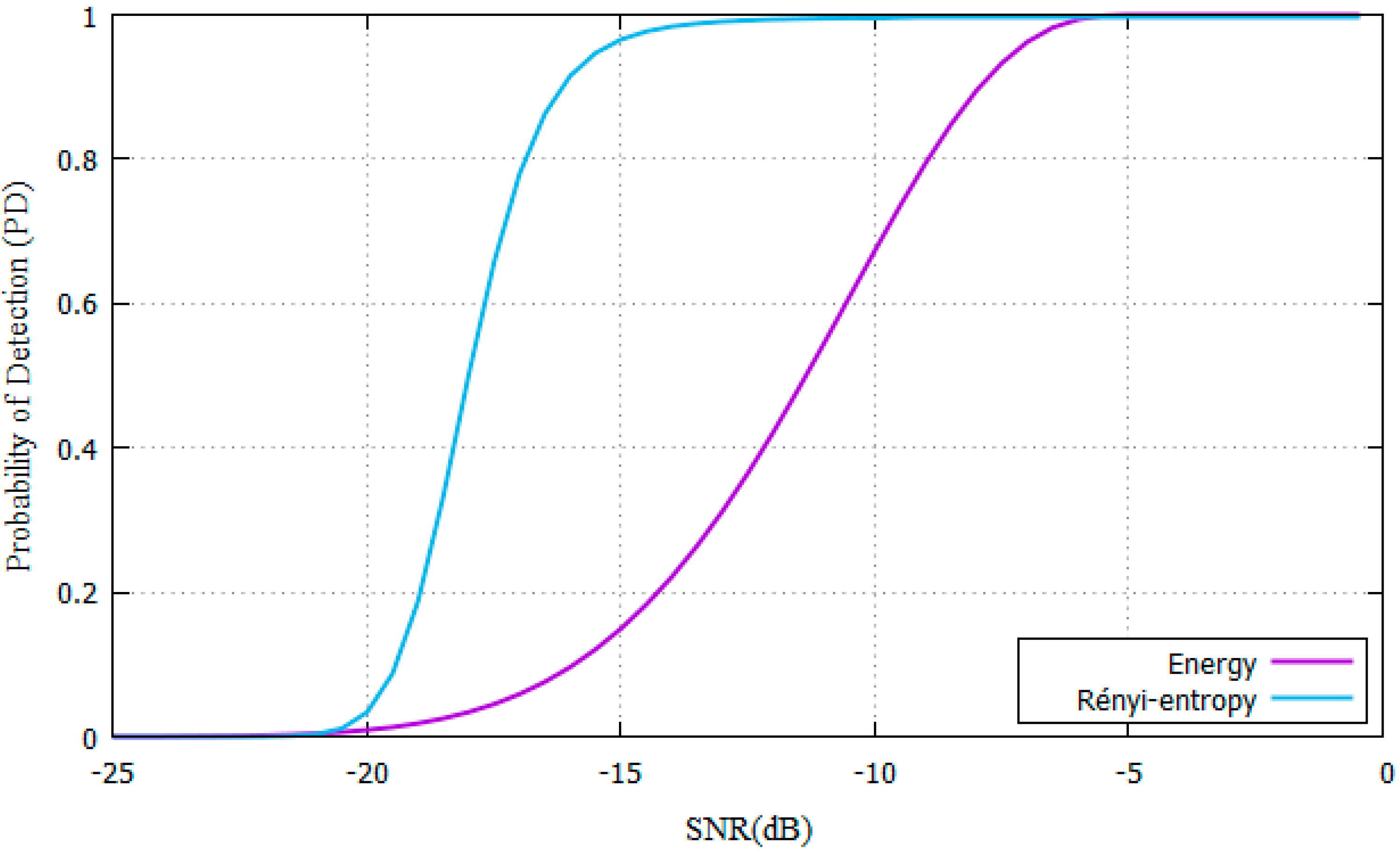
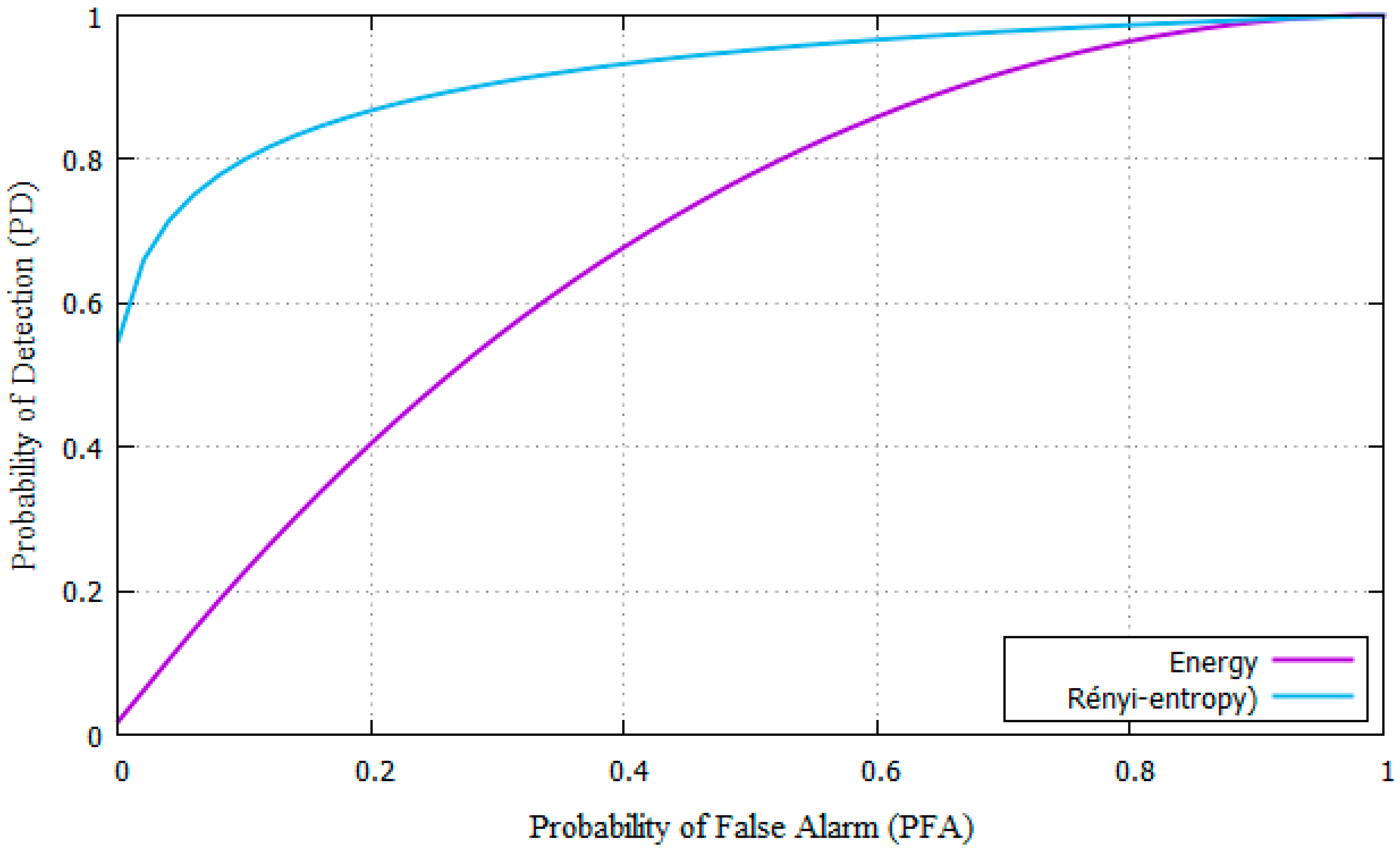
4.1. Simulation Results
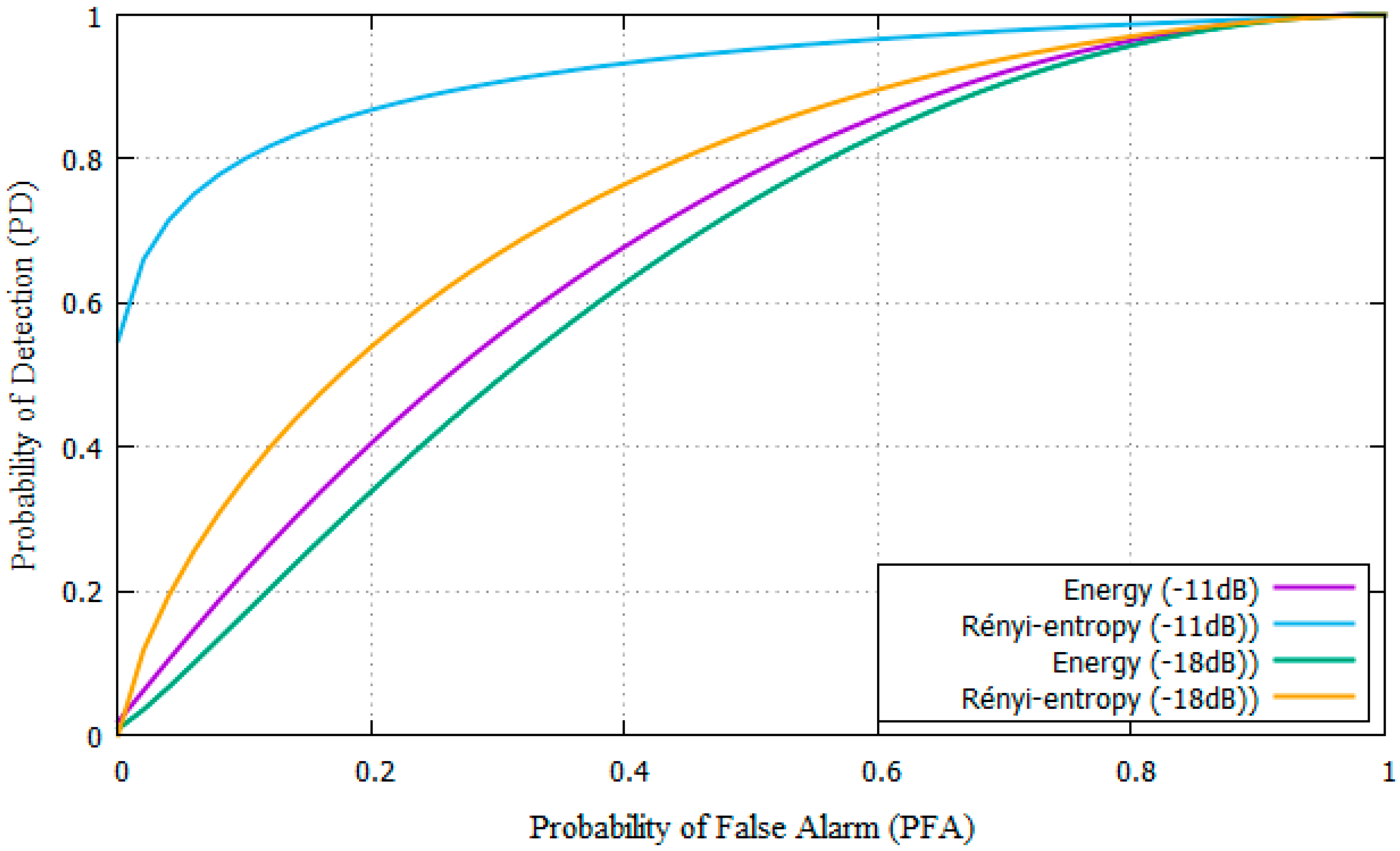
4.2. Software Defined Radio Experimental Results
4.2.1. GMSK Experiments
4.2.2. OFDM Experiments
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mitola, J. Software radios: Survey, critical evaluation and future directions. IEEE Aerosp. Electron. Syst. Mag. 1993, 8, 25–36. [Google Scholar] [CrossRef]
- Nijsure, Y.; Kaddoum, G.; Ghodoosipour, G.; Cai, G.; Wang, L. A novel spectrum sensing mechanism based on distribution discontinuity estimation within cognitive radio. In Proceedings of the 2016 IEEE 84th Vehicular Technology Conference (VTC-Fall), Montreal, QC, Canada, 18–21 September 2016; pp. 1–5. [Google Scholar]
- Khader, A.A.-H.; Shabani, A.M.H.; Beg, M.T. Differentiation and discrimination between GSM and WiMAX signal’s technologies. In Proceedings of the 2014 World Congress on Computer Applications and Information Systems (WCCAIS), Hammamet, Tunisia, 17–19 January 2014; pp. 1–6. [Google Scholar]
- An, C.; Ryu, H.-G. CPW-OFDM (Cyclic Postfix Windowing OFDM) for the B5G (Beyond 5th Generation) Waveform. In Proceedings of the 2018 IEEE 10th Latin-American Conference on Communications (LATINCOM), Guadalajara, Mexico, 14–16 November 2018; pp. 1–4. [Google Scholar]
- Mrkic, J.; Kocan, E.; Pejanovic-Djurisic, M. Index modulation techniques in OFDM relay systems for 5G wireless networks. In Proceedings of the 2017 40th International Conference on Telecommunications and Signal Processing (TSP), Barcelona, Spain, 5–7 July 2017; pp. 208–211. [Google Scholar]
- Khasawneh, M.; Agarwal, A. A survey on security in Cognitive Radio networks. In Proceedings of the 2014 6th International Conference on Computer Science and Information Technology (CSIT), Amman, Jordan, 26–27 March 2014; pp. 64–70. [Google Scholar]
- Srinu, S.; Sabat, S.L.; Udgata, S.K. Spectrum Sensing using Frequency domain Entropy estimation and its FPGA implementation for Cognitive Radio. Procedia Eng. 2012, 30, 289–296. [Google Scholar] [CrossRef]
- Pedraza, L.F.; Forero, F.; Páez, I.P. Detección de espectro para radio cognitiva. Ingeniare Rev. Chil. Ing. 2012, 20, 197–210. [Google Scholar] [CrossRef]
- Amrutha, V.; Karthikeyan, K. Spectrum sensing methodologies in cognitive radio networks: A survey. In Proceedings of the 2017 International Conference on Innovations in Electrical, Electronics, Instrumentation and Media Technology (ICEEIMT), Coimbatore, India, 3–4 February 2017; pp. 306–310. [Google Scholar]
- Mandal, A.; Chatterjee, S. A comprehensive Study on spectrum sensing and resource allocation for cognitive cellular network. In Proceedings of the 2017 Devices for Integrated Circuit (DevIC), Kalyani, India, 23–24 March 2017; pp. 100–102. [Google Scholar]
- Zhang, Y.L.; Zhang, Q.Y.; Melodia, T. A frequency-domain entropy-based detector for robust spectrum sensing in cognitive radio networks. IEEE Commun. Lett. 2010, 14, 533–535. [Google Scholar] [CrossRef]
- Hossain, E.; Niyato, D.; Han, Z. Dynamic Spectrum Access and Management in Cognitive Radio Networks; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Akyildiz, I.F.; Lee, W.-Y.; Vuran, M.C.; Mohanty, S. A survey on spectrum management in cognitive radio networks. IEEE Commun. Mag. 2008, 46, 40–48. [Google Scholar] [CrossRef]
- Vamvakas, P.; Tsiropoulou, E.E.; Papavassiliou, S. On Controlling Spectrum Fragility via Resource Pricing in 5G Wireless Networks. IEEE Netw. Lett. 2019, 1, 111–115. [Google Scholar] [CrossRef]
- So, J. Entropy-based Spectrum Sensing for Cognitive Radio Networks in the Presence of an Unauthorized Signal. KSII Trans. Internet Inf. Syst. 2015, 9. [Google Scholar] [CrossRef]
- Chen, X.; Nagaraj, S. Entropy based spectrum sensing in cognitive radio. In Proceedings of the 2008 Wireless Telecommunications Symposium, Pomona, CA, USA, 24–26 April 2008; pp. 57–61. [Google Scholar]
- Verdú, S. Empirical Estimation of Information Measures: A Literature Guide. Entropy 2019, 21, 720. [Google Scholar] [CrossRef]
- Bromiley, P.; Thacker, N.; Bouhova-Thacker, E. Shannon Entropy, Renyi Entropy, and Information; Statistics and Inf. Series (2004-004); The University of Manchester: Manchester, UK, 2004. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Contributions to the Theory of Statistics; University of California Press: Berkeley, CA, USA, 1961. [Google Scholar]
- Eggels, A.; Crommelin, D. Quantifying Data Dependencies with Rényi Mutual Information and Minimum Spanning Trees. Entropy 2019, 21, 100. [Google Scholar] [CrossRef]
- Lapidoth, A.; Pfister, C. Two measures of dependence. Entropy 2019, 21, 778. [Google Scholar] [CrossRef]
- Cai, C.; Verdú, S. Conditional Rényi Divergence Saddlepoint and the Maximization of α-Mutual Information. Entropy 2019, 21, 969. [Google Scholar] [CrossRef]
- Ansari, M.H.; van Steensel, A.; Nazarov, Y.V. Entropy production in quantum is different. Entropy 2019, 21, 854. [Google Scholar] [CrossRef]
- Aswathy, G.; Gopakumar, K. Cognitive Radio Network with Wideband Spectrum Sensing and Reliable Data Transmission. In Proceedings of the 2018 IEEE Recent Advances in Intelligent Computational Systems (RAICS), Thiruvananthapuram, India, 6–8 December 2018; pp. 70–74. [Google Scholar]
- Zhu, W.; Ma, J.; Faust, O. A comparative study of different entropies for spectrum sensing techniques. Wirel. Pers. Commun. 2013, 69, 1719–1733. [Google Scholar] [CrossRef]
- Wei, Y.; Fang, S.; Wang, X. Automatic Modulation Classification of Digital Communication Signals Using SVM Based on Hybrid Features, Cyclostationary, and Information Entropy. Entropy 2019, 21, 745. [Google Scholar] [CrossRef]
- ETSI, T. 145 005 Digital Cellular Telecommunications System (Phase 2+); Radio Transsmision and Reception (3GPP TS 45.005 version 12.5. 0 Release 12). Sophia Antipolis Cedex April; ETSI 3GPP. 2015. Available online: http://www.etsi.org (accessed on 1 November 2019).
- Jin, F.; Varadharajan, V.; Tupakula, U. Improved detection of primary user emulation attacks in cognitive radio networks. In Proceedings of the 2015 International Telecommunication Networks and Applications Conference (ITNAC), Sydney, Australia, 18–20 November 2015; pp. 274–279. [Google Scholar]
- Chandwani, N.; Jain, A.; Vyavahare, P.D. Throughput comparison for Cognitive Radio network under various conditions of primary user and channel noise signals. In Proceedings of the 2015 Radio and Antenna Days of the Indian Ocean (RADIO), Belle Mare, Mauritius, 21–24 September 2015; pp. 1–2. [Google Scholar]
- Valverde-Albacete, F.J.; Peláez-Moreno, C. The Rényi Entropies Operate in Positive Semifields. Entropy 2019, 21, 780. [Google Scholar] [CrossRef]
- Burgess, D.A.; Samra, H.S. The Openbts Project. 2008. Available online: http://openbts.sourceforge.net (accessed on 1 November 2019).
- Iedema, M. Getting Started with OpenBTS: Build Open Source Mobile Networks; O’Reilly Media, Inc.: Sevastopol, CA, USA, 2014. [Google Scholar]
- Abirami, M.; Hariharan, V.; Sruthi, M.; Gandhiraj, R.; Soman, K. Exploiting GNU radio and USRP: An economical test bed for real time communication systems. In Proceedings of the 2013 Fourth International Conference on Computing, Communications and Networking Technologies (ICCCNT), Tiruchengode, India, 4–6 July 2013; pp. 1–6. [Google Scholar]
- Garcia, J.H.H.A.; Rodríguez, C.J.P.; Ruiz, F.E.Ñ.; Alarcón, J.L.A. Implementación de una red celular GSM mediante software OPENBTS. Pueblo Cont. 2019, 30, 101–108. [Google Scholar]
- Mohamoud, M.A.; Elsheikh, E.M.A.; Habaebi, M.H. A comparative study of energy detector performance under AWGN and fading channels. In Proceedings of the 2016 International Conference on Advances in Electrical, Electronic and Systems Engineering (ICAEES), Putrajaya, Malaysia, 14–16 November 2016; pp. 89–94. [Google Scholar]
- Liu, X.; Evans, B.G.; Moessner, K. Comparison of reliability, delay and complexity for standalone cognitive radio spectrum sensing schemes. IET Commun. 2013, 7, 799–807. [Google Scholar] [CrossRef]
- Lopez-Lopez, L.; Cardenas-Juarez, M.; Stevens-Navarro, E.; Pineda-Rico, U.; Arce, A.; Orozco-Lugo, A.G. Superimposed Training Combined Approach for a Reduced Phase of Spectrum Sensing in Cognitive Radio. Sensors 2019, 19, 2425. [Google Scholar] [CrossRef] [PubMed]



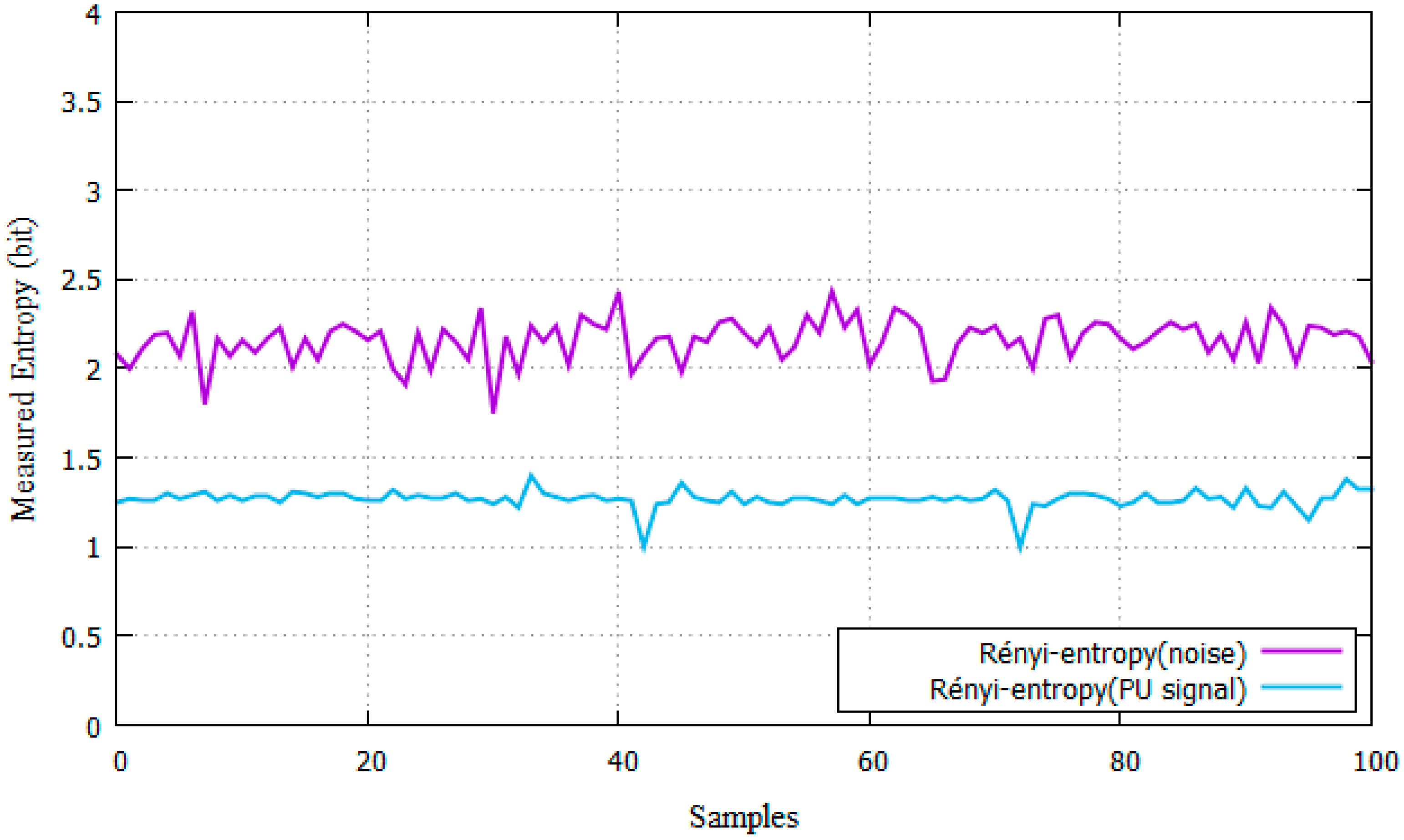
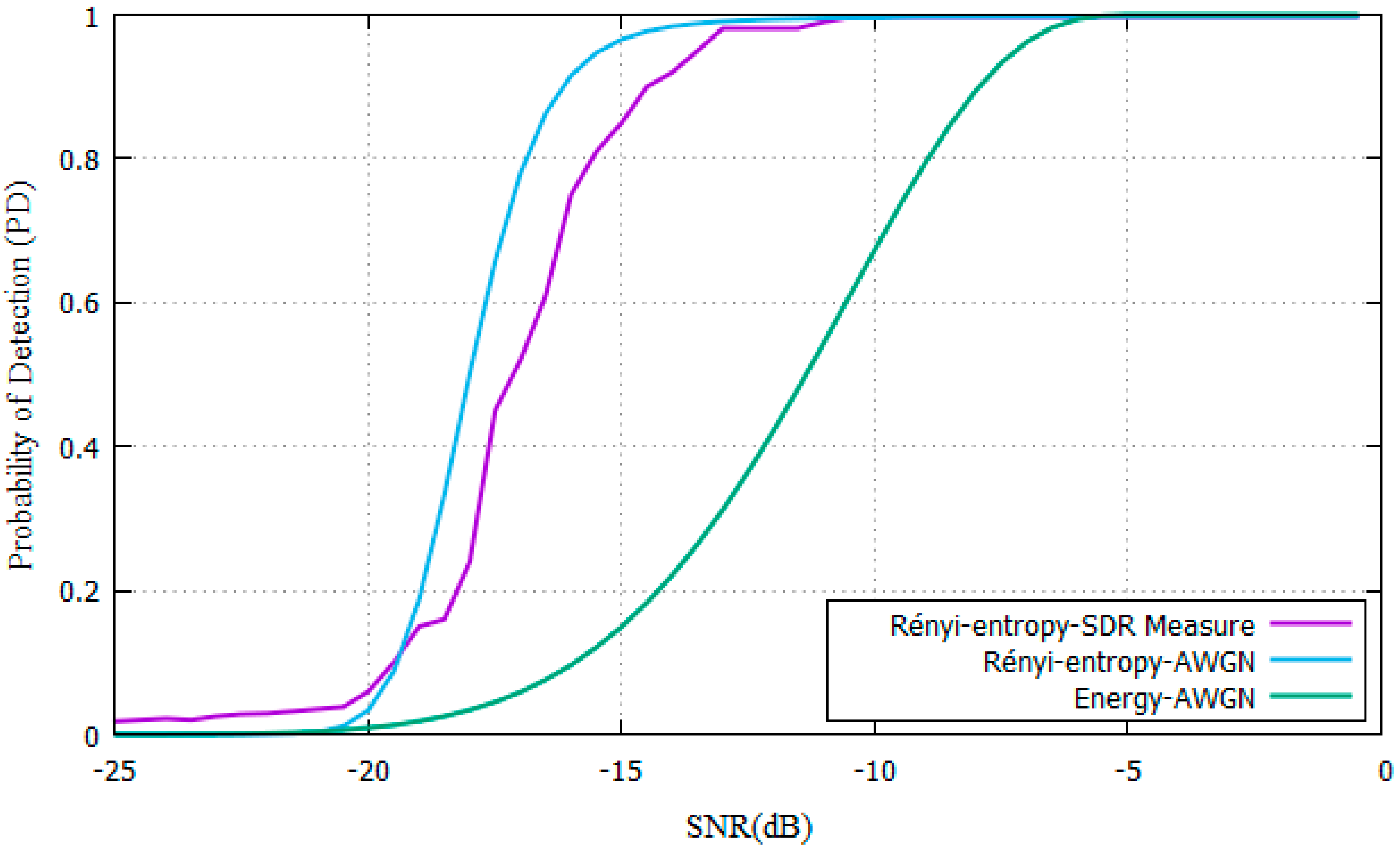

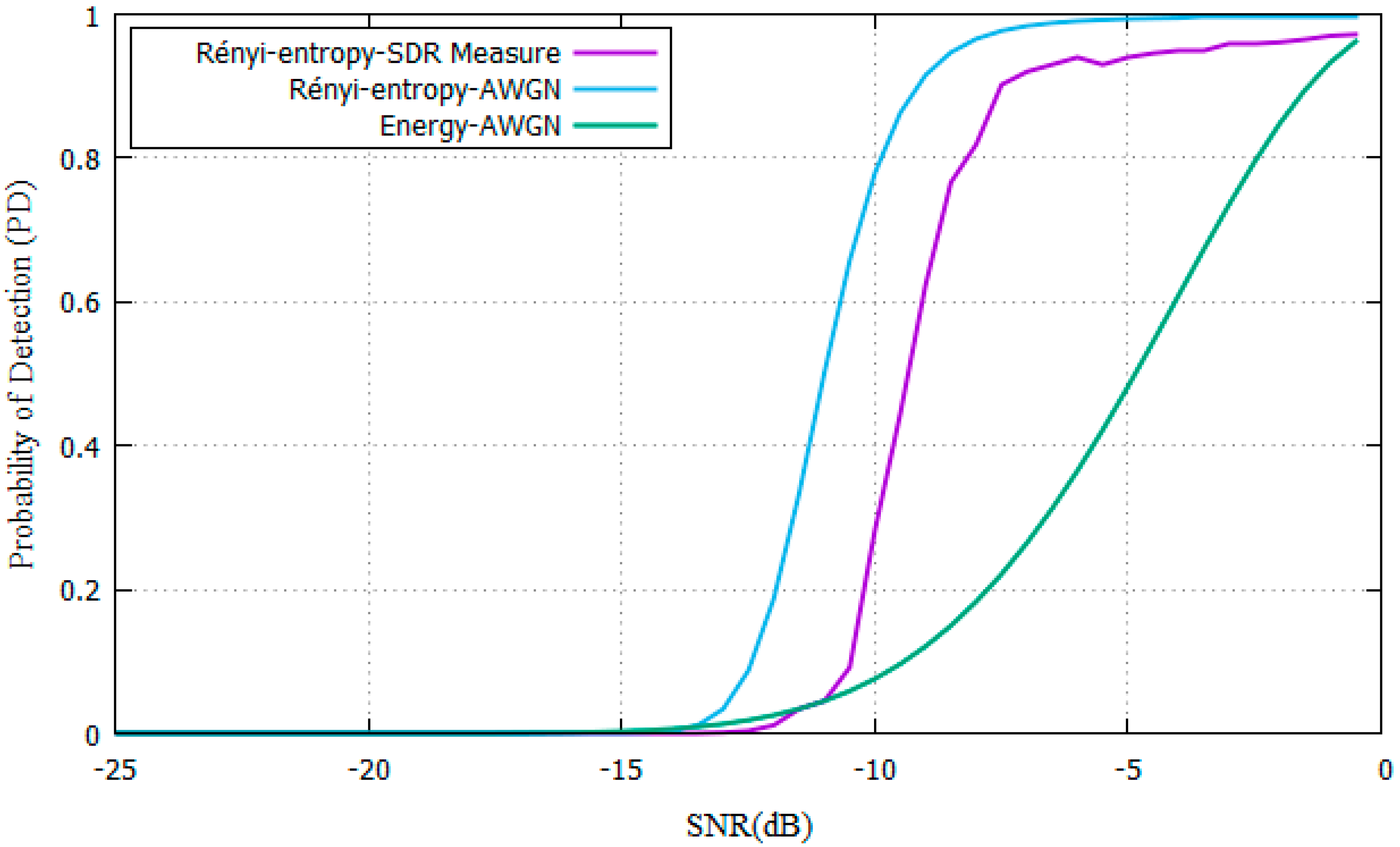
| Parameter | Description |
|---|---|
| Number of samples | 10,000 |
| PU | 2 |
| SU | 2 |
| Number of bins L | 15 |
| Estimated PFA | <0.1 |
| Objective PD | >0.9 |
| Signal Noise | AWGN/Rayleigh |
| Primary Signal | GMSK /OFDM |
| Bandwidth | 12 kHz |
| Symbol Ratio | 10 kbps |
| Carrier Frequency | 40 kHz |
| Sampling Frequency | 100 kHz |
| DFT size | 128 |
| Average Noise Power | −90 dBm |
| α | 2.5 |
| Confidence level | 95% |
| Error | 5% |
| Parameter | Description |
|---|---|
| Number of samples | 15,000 |
| Number of SU | 2 |
| Number of SU | 2 |
| Service | Phone Call |
| Distance of PU to MCBS | 0–5 m |
| Primary Signal | GSMK |
| Bandwidth | 831.8 MHz |
| Confidence level | 95% |
| Error | 5% |
| Parameter | Description |
|---|---|
| Number of samples | 600 |
| Encoded polynomial | [171–133] |
| Modulation | OFDM |
| Number of SU | 2 |
| Service | Tx-Rx |
| Distance of PU to MCBS | 0–5 m |
| Number of sub-carriers | 64 |
| Bandwidth | 831.8 MHz |
| Confidence level | 95% |
| Error | 5% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cadena Muñoz, E.; Pedraza Martínez, L.F.; Hernandez, C.A. Rényi Entropy-Based Spectrum Sensing in Mobile Cognitive Radio Networks Using Software Defined Radio. Entropy 2020, 22, 626. https://doi.org/10.3390/e22060626
Cadena Muñoz E, Pedraza Martínez LF, Hernandez CA. Rényi Entropy-Based Spectrum Sensing in Mobile Cognitive Radio Networks Using Software Defined Radio. Entropy. 2020; 22(6):626. https://doi.org/10.3390/e22060626
Chicago/Turabian StyleCadena Muñoz, Ernesto, Luis Fernando Pedraza Martínez, and Cesar Augusto Hernandez. 2020. "Rényi Entropy-Based Spectrum Sensing in Mobile Cognitive Radio Networks Using Software Defined Radio" Entropy 22, no. 6: 626. https://doi.org/10.3390/e22060626
APA StyleCadena Muñoz, E., Pedraza Martínez, L. F., & Hernandez, C. A. (2020). Rényi Entropy-Based Spectrum Sensing in Mobile Cognitive Radio Networks Using Software Defined Radio. Entropy, 22(6), 626. https://doi.org/10.3390/e22060626






