Tsallis Entropy for Cross-Shareholding Network Configurations
Abstract
1. Introduction
2. Brief Review of the Reference Literature on Cross-Shareholdings
3. Methodology
3.1. Preliminaries and Notations
Reasoning behind the Tsallis Entropy
3.2. Outline of the Analysis
- Product (independence)
- Lower Frechet (maximal negative dependence) and Upper Frechet (maximal positive dependence)
- Power law:where , is a normalising constant and .
- Exponential law:where , is a normalising constant and .
- (A)
- under the hypothesis of described by a power law as in (6) and has its empirical distribution, the power law exponent k is allowed to change and is treated as a parameter;
- (B)
- under the hypothesis of power law as in (6) and empirical: the power law exponent k is allowed to change and is treated as a parameter; and,
- (C)
- under the hypothesis of exponential as in (7) and empirical: the parameter k in the exponential is allowed to change, as any parameter does.
4. The Network
4.1. The Data
4.2. Construction of the Network
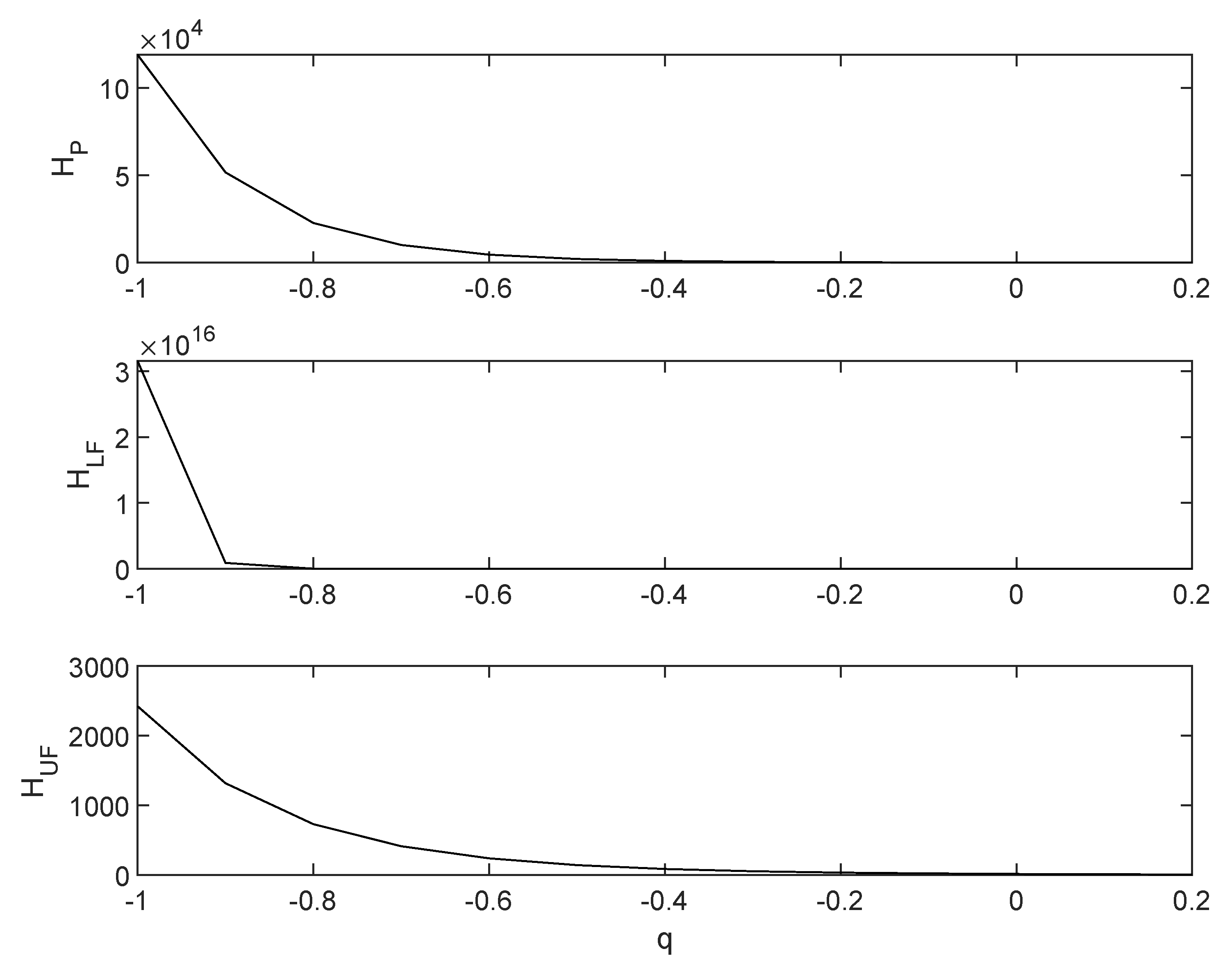
5. Results and Discussion
6. Conclusions and Policy Implications
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Contreras, M.G.A.; Fagiolo, G. Propagation of economic shocks in input-output networks: A cross-country analysis. Phys. Rev. E 2014, 90, 062812. [Google Scholar] [CrossRef] [PubMed]
- Ohnishi, T.; Takayasu, H.; Takayasu, M. Hubs and authorities on Japanese inter-firm network: Characterisation of nodes in very large directed networks. Prog. Theor. Phys. Suppl. 2009, 179, 157–166. [Google Scholar] [CrossRef]
- Luo, J. The power-of-pull of economic sectors: A complex network analysis. Complexity 2013, 18, 37–47. [Google Scholar] [CrossRef]
- Maluck, J.; Donner, R.V. A network of networks perspective on global trade. PLoS ONE 2015, 10, e0133310. [Google Scholar] [CrossRef] [PubMed]
- Ferraro, G.; Iovanella, A. Technology transfer in innovation networks: An empirical study of the Enterprise Europe Network. Int. J. Eng. Bus. Manag. 2017, 9, 1–14. [Google Scholar] [CrossRef]
- Gulati, R.; Westphal, J.D. Cooperative or controlling? The effects of CEO-board relations and the content of interlocks on the formation of joint ventures. Adm. Sci. Q. 1999, 44, 473–506. [Google Scholar] [CrossRef]
- Ceptureanu, S.I.; Ceptureanu, E.G.; Marin, I. Assessing role of strategic choice on organisational performance by Jacquemin- Berry entropy index. Entropy 2017, 19, 448. [Google Scholar] [CrossRef]
- Ferraro, G.; Iovanella, A. Organizing collaboration in inter-organisational innovation networks, from orchestration to choreography. Int. J. Eng. Bus. Manag. 2015, 7, 7–24. [Google Scholar] [CrossRef]
- Bellenzier, L.; Grassi, R. Interlocking directorates in Italy: Persistent links in network dynamics. J. Econ. Interact. Coord. 2014, 9, 183–202. [Google Scholar] [CrossRef]
- Chapelle, A.; Szafarz, A. Controlling Firms Through the Majority Voting Rule. Physica A 2005, 355, 509–529. [Google Scholar] [CrossRef]
- Croci, E.; Grassi, R. The economic effect of interlocking directorates in Italy: New evidence using centrality measures. Comput. Math. Org. Theory 2014, 20, 89–112. [Google Scholar] [CrossRef]
- Rotundo, G.; D’Arcangelis, A.M. Network analysis of ownership and control structure in the Italian Stock market. Adv. Appl. Stat. Sci. 2010, 2, 255–273. [Google Scholar]
- Ceptureanu, E.G.; Ceptureanu, S.I. Popescu D. Relationship between Entropy, Corporate Entrepreneurship and Organisational Capabilities in Romanian Medium Sized Enterprises. Entropy 2017, 19, 412. [Google Scholar] [CrossRef]
- Weber, S.; Weske, K. The joint impact of bankruptcy costs, fire sales and cross-holdings on systemic risk in financial networks. Probab. Uncertain. Quant. Risk 2017, 2, 9. [Google Scholar] [CrossRef]
- Aoyama, H.; Fujiwara, Y.; Ikeda, Y.; Iyetomi, H.; Souma, W. Econophysics and Companies: Statistical Life and Death in Complex Business Networks; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Delpini, D.; Battiston, S.; Riccaboni, M.; Gabbi, G.; Pammolli, F.; Caldarelli, G. Evolution of controllability in interbank networks. Sci. Rep. 2013, 3, 1626. [Google Scholar] [CrossRef] [PubMed]
- Clementi, F.; Gallegati, M. Pareto’s law of income distribution: Evidence for Germany, the United Kingdom, and the United States. In Econophysics of Wealth Distributions; Chatterjee, A., Yarlagadda, S., Chakrabarti, B.K., Eds.; Springer: Milan, Italy, 2005; pp. 3–14. [Google Scholar]
- Gao, J.; Barzel, B.; Barabasi, A.L. Universal resilience patterns in complex networks. Nature 2016, 530, 307–312. [Google Scholar] [CrossRef] [PubMed]
- Iori, G.; De Masi, G.; Precup, O.V.; Gabbi, G.; Caldarelli, G. A network analysis of the Italian overnight money market. J. Econ. Dyn. Control 2008, 32, 259–278. [Google Scholar] [CrossRef]
- Newman, M.; Barabasi, A.L.; Watts, D.J. The Structure and Dynamics of Networks; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Soramaki, K.; Bech, M.L.; Arnold, J.; Glass, R.J.; Beyeler, W.E. The topology of interbank payment flows. Phys. A Stat. Mech. Appl. 2007, 379, 317–333. [Google Scholar] [CrossRef]
- Elliott, M.; Golub, B.; Jackson, M.O. Financial networks and contagion. Am. Econ. Rev. 2014, 104, 3115–3153. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalisation of Boltzmann-Gibbs Statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Maszczyk, T.; Duch, W. Comparison of Shannon, Renyi and Tsallis Entropy Used in Decision Trees. In Artificial Intelligence and Soft Computing—ICAISC 2008; Rutkowski, L., Tadeusiewicz, R., Zadeh, L.A., Zurada, J.M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5097, pp. 643–651. [Google Scholar]
- Rotundo, G.; Ausloos, M. Complex-valued information entropy measure for networks with directed links (digraphs). Application to citations by community agents with opposite opinions. Eur. Phys. J. B 2013, 86, 169. [Google Scholar] [CrossRef]
- Shannon, C.E.; Weaver, W. The Mathematical Theory of Communication; University of Illinois Press: Urbana, IL, USA, 1949. [Google Scholar]
- Cerqueti, R.; Rotundo, G.; Ausloos, M. Investigating the configurations in cross-shareholding: A joint copula-entropy approach. Entropy 2017, 20, 134. [Google Scholar] [CrossRef]
- Tsallis, C. Economics and Finance: q-Statistical Stylized Features Galore. Entropy 2017, 19, 457. [Google Scholar] [CrossRef]
- Ausloos, M.; Ivanova, K. Dynamical model and nonextensive statistical mechanics of a market index on large time windows. Phys. Rev. E 2003, 68, 046122. [Google Scholar] [CrossRef]
- Ausloos, M.; Miskiewicz, J. Introducing the q-Theil index. Braz. J. Phys. 2009, 39, 388–395. [Google Scholar]
- Devi, S. Financial portfolios based on Tsallis relative entropy as the risk measure. J. Stat. Mech. Theory Exp. 2019, 2019, 093207. [Google Scholar] [CrossRef]
- Maasoumi, E.; Racine, J. Entropy and predictability of stock market returns. J. Econ. 2002, 107, 291–312. [Google Scholar] [CrossRef]
- Vințe, C.; Smeureanu, I.; Furtună, T.-F.; Ausloos, M. An Intrinsic Entropy Model for Exchange-Traded Securities. Entropy 2019, 21, 1173. [Google Scholar] [CrossRef]
- Zhou, R.; Cai, R.; Tong, G. Applications of entropy in finance: A review. Entropy 2013, 15, 4909–4931. [Google Scholar] [CrossRef]
- Wilk, G.; Włodarczyk, Z. Tsallis distribution with complex nonextensivity parameter q. Phys. A Stat. Mech. Appl. 2014, 413, 53–58. [Google Scholar] [CrossRef]
- Frechet, M. Remarques au sujet de la note précédente. C. R. Acad. Sci. Paris 1958, 246, 2719–2720. [Google Scholar]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; CRC Press: London, UK; New York, NY, USA, 1997. [Google Scholar]
- Nelsen, R.B. An Introduction to Copulas; Springer: New York, NY, USA, 1999. [Google Scholar]
- Sklar, M. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Caldarelli, G. Scale-Free Networks: Complex Webs in Nature and Technology; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Gandy, A.; Veraart, L.A.M. A Bayesian methodology for systemic risk assessment in financial networks. Manag. Sci. 2016, 63, 4428–4446. [Google Scholar] [CrossRef]
- Cimini, G.; Serri, M. Entangling credit and funding shocks in interbank markets. PLoS ONE 2016, 11, e0161642. [Google Scholar] [CrossRef] [PubMed]
- Cinelli, M.; Ferraro, G.; Iovanella, A. Rich-club ordering and the dyadic effect: Two interrelated phenomena. Phys. A Stat. Mech. Appl. 2018, 490, 808–818. [Google Scholar] [CrossRef]
- Cinelli, M.; Ferraro, G.; Iovanella, A. Structural bounds on the dyadic effect. J. Complex Netw. 2017, 5, 694–711. [Google Scholar] [CrossRef]
- Cinelli, M.; Iovanella, A.; Ferraro, G.; Rotundo, G. Assessing the impact of incomplete information on the resilience of financial networks. Ann. Oper. Res. 2019. Available online: https://doi.org/10.1007/s10479-019-03306-y (accessed on 1 January 2020). [CrossRef]
- D’Arcangelis, A.M.; Rotundo, G. Systemic Risk of Non Performing Loans Market. The Italian case. J. Appl. Quant. Methods 2019, 14. Available online: http://jaqm.ro/issues/volume-14,issue-1/0_A_G.PHP (accessed on 1 January 2020).
- D’Errico, M.; Grassi, R.; Stefani, S.; Torriero, A. Shareholding Networks and Centrality: An Application to the Italian Financial Market. In Networks, Topology and Dynamics; Naimzada, A.K., Stefani, S., Torriero, A., Eds.; Lecture Notes in Economics and Mathematical Systems; Springer: Berlin/ Heidelberg, Germany, 2009; Volume 613, pp. 215–228. [Google Scholar]
- Abreu, M.P.; Grassi, R.; Del-Vecchio, R.R. Structure of control in financial networks: An application to the Brazilian stock market. Phys. A Stat. Mech. Appl. 2019, 522, 302–314. [Google Scholar] [CrossRef]
- Bebchuk, L.A.; Kraakman, R.; Triantis, G. Stock pyramids, cross-ownership, and dual class equity: The mechanisms and agency costs of separating control from cash-flow rights. In Concentrated Corporate Ownership; Morck, R.K., Ed.; University of Chicago Press: Chicago, IL, USA, 2017; pp. 295–318. [Google Scholar]
- Vitali, S.; Glattfelder, J.B.; Battiston, S. The network of global corporate control. PLoS ONE 2011, 6, e25995. [Google Scholar] [CrossRef]
- Lichtenberg, F.R.; Pushner, G.M. Ownership structure and corporate performance in Japan. Jpn. World Econ. 1994, 6, 239–261. [Google Scholar] [CrossRef]
- Okabe, M. Cross Shareholdings in Japan. A New Unified Perspective of the Economic System; Edward Elgar: Cheltenham, UK, 2002. [Google Scholar]
- Souma, W.; Fujiwara, Y.; Aoyama, H. Change of ownership networks in Japan. In Practical Fruits of Econophysics; Takayasu, H., Ed.; Springer: Tokyo, Japan, 2006; pp. 307–311. [Google Scholar]
- Garlaschelli, D.; Battiston, S.; Castri, M.; Servedio, V.; Caldarelli, G. The scale-free topology of market investments. Phys. A Stat. Mech. Appl. 2005, 350, 491–499. [Google Scholar] [CrossRef]
- Chang, X.; Wang, H. Cross-Shareholdings Structural Characteristic and Evolution Analysis Based on Complex Network. Discrete Dyn. Nat. Soc. 2017, 2017, 5801386. [Google Scholar]
- Rotundo, G.; D’Arcangelis, A.M. Network of companies: An analysis of market concentration in the Italian stock market. Qual. Quant. 2014, 48, 1893–1910. [Google Scholar] [CrossRef]
- Barbosa, C.S.; Caraballo, R.; Alves, L.R.; Hartmann, G.A.; Beggan, C.D.; Viljanen, A.; Ngwira, C.M.; Papa, A.R.R.; Pirjola, R.J. The Tsallis statistical distribution applied to geomagnetically induced currents. Space Weather 2017, 15, 1094–1101. [Google Scholar] [CrossRef]
- Petroni, F.; Ausloos, M. High frequency (daily) data analysis of the Southern Oscillation Index. Tsallis nonextensive statistical mechanics approach. Eur. Phys. J. Spec. Top. 2007, 143, 201–208. [Google Scholar] [CrossRef]
- Bila, L.; Grech, D.; Podhajska, E. Methods of Non-Extensive Statistical Physics in Analysis of Price Returns on Polish Stock Market. Acta Phys. Polonica A 2016, 129, 986–992. [Google Scholar] [CrossRef]
- Jakimowicz, A. The Role of Entropy in the Development of Economics. Entropy 2020, 22, 452. [Google Scholar] [CrossRef]
- Queiros, S.D.; Moyano, L.G.; De Souza, J.; Tsallis, C. A nonextensive approach to the dynamics of financial observables. Eur. Phys. J. B 2007, 55, 161–167. [Google Scholar] [CrossRef]
- Rak, R.; Drożdż, S.; Kwapień, J. Nonextensive statistical features of the Polish stock market fluctuations. Phys. A Stat. Mech. Appl. 2007, 374, 315–324. [Google Scholar] [CrossRef]
- Rak, R.; Drożdż, S.; Kwapień, J.; Oswiecimka, P. Stock returns versus trading volume: Is the correspondence more general? Acta Phys. Pol. B 2013, 44, 2035–2050. [Google Scholar] [CrossRef]
- Ruseckas, J.; Gontis, V.; Kaulakys, B. Nonextensive statistical mechanics distributions and dynamics of financial observables from the nonlinear stochastic differential equations. Adv. Complex Syst. 2012, 15, 1250073. [Google Scholar] [CrossRef]
- Pavlos, G.P.; Karakatsanis, L.P.; Iliopoulos, A.C.; Pavlos, E.G.; Tsonis, A.A. Non-extensive statistical mechanics: Overview of theory and applications in seismogenesis, climate, and space plasma. In Advances in Nonlinear Geosciences; Tsonis, A., Ed.; Springer: Cham, Switzerland, 2018; pp. 465–495. [Google Scholar]
- Gell-Mann, M.; Tsallis, C. (Eds.) Nonextensive Entropy: Interdisciplinary Applications; Oxford University Press on Demand: Oxford, UK, 2004. [Google Scholar]
- Rotundo, G.; D’Arcangelis, A.M. Ownership and control in shareholding networks. J. Econ. Interact. Coord. 2010, 5, 191–219. [Google Scholar] [CrossRef]
- Li, H.; Fang, W.; An, H.; Yan, L. The shareholding similarity of the shareholders of the worldwide listed energy companies based on a two-mode primitive network and a one-mode derivative holding-based network. Phys. A Stat. Mech. Appl. 2014, 415, 525–532. [Google Scholar] [CrossRef]
- Li, H.; An, H.; Gao, X.; Huang, J.; Xu, Q. On the topological properties of the cross-shareholding networks of listed companies in China: Taking shareholders’ cross-shareholding relationships into account. Phys. A Stat. Mech. Appl. 2014, 406, 80–88. [Google Scholar] [CrossRef]
- US Mergers Guidelines. Available online: http://www.stanfordlawreview.org/online/obama-antitrust-enforcement (accessed on 13 June 2020).
- Horizontal Merger Guidelines. Available online: https://www.justice.gov/atr/horizontal-merger-guidelines-0 (accessed on 13 June 2020).
- Crane, D.A. Has the Obama Justice Department reinvigorated antitrust enforcement? Stanf. Law Rev. Online 2012, 65, 13–20. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cerqueti, R.; Rotundo, G.; Ausloos, M. Tsallis Entropy for Cross-Shareholding Network Configurations. Entropy 2020, 22, 676. https://doi.org/10.3390/e22060676
Cerqueti R, Rotundo G, Ausloos M. Tsallis Entropy for Cross-Shareholding Network Configurations. Entropy. 2020; 22(6):676. https://doi.org/10.3390/e22060676
Chicago/Turabian StyleCerqueti, Roy, Giulia Rotundo, and Marcel Ausloos. 2020. "Tsallis Entropy for Cross-Shareholding Network Configurations" Entropy 22, no. 6: 676. https://doi.org/10.3390/e22060676
APA StyleCerqueti, R., Rotundo, G., & Ausloos, M. (2020). Tsallis Entropy for Cross-Shareholding Network Configurations. Entropy, 22(6), 676. https://doi.org/10.3390/e22060676





