Entropy Analysis of a Flexible Markovian Queue with Server Breakdowns
Abstract
1. Introduction
2. Model Formulation and Previous Results
3. Entropy Approach
3.1. Entropy Solution Using the First Moment
3.2. Entropy Solution Using the Second Moment
3.3. Entropy Solution Using Both First and Second Moments
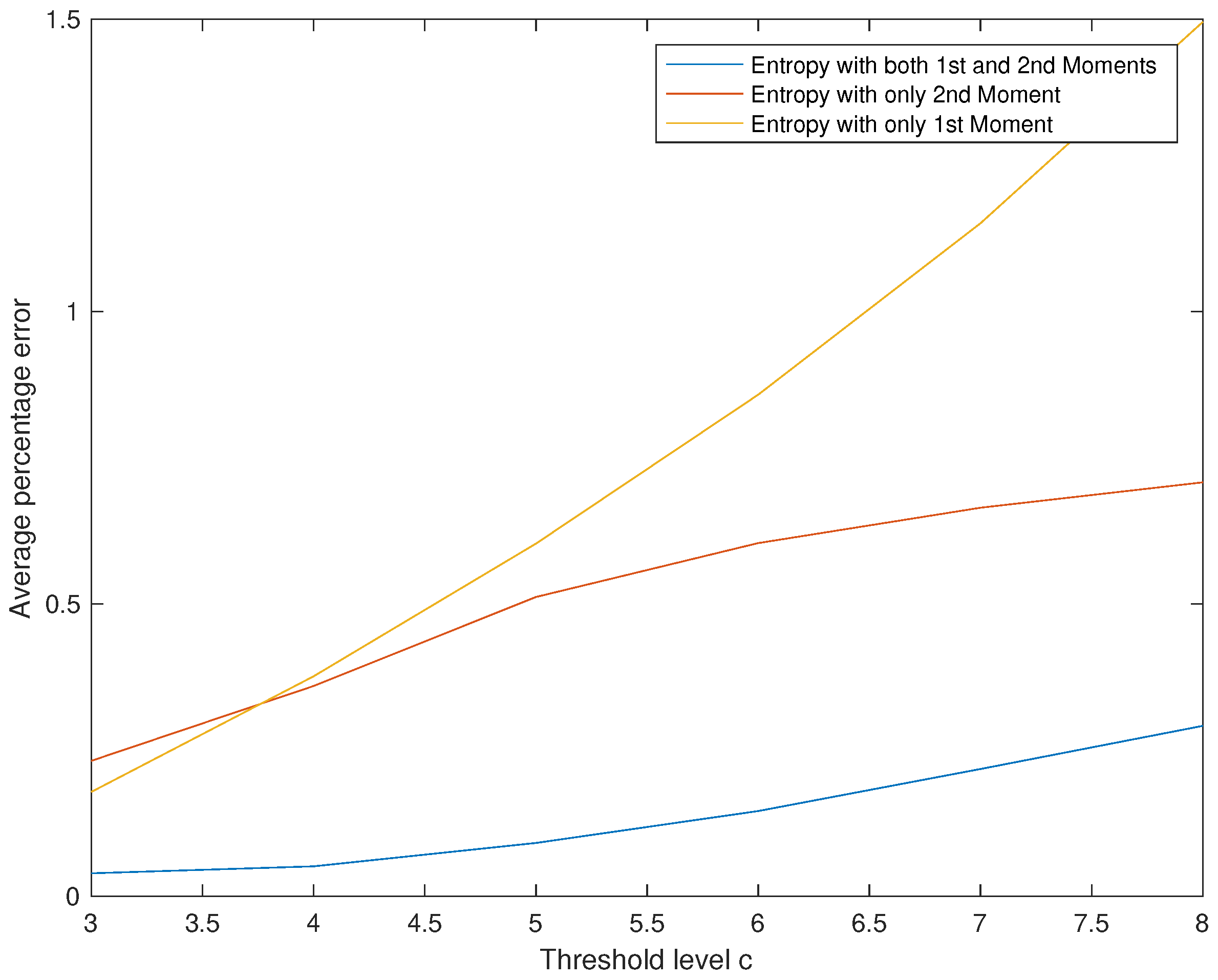
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Kapur, J.N. Maximum Entropy Models in Science and Engineering; Wiley Eastern Limited: New Delhi, India, 1989. [Google Scholar]
- Bechtold, W.R.; Medlin, J.E.; Weber, D.R. PCM Telemetry Data Compression Study, Phase 1 Final Report, Prepared by Lockheed Missiles & Space Company Sunnyvale, California for Goddard Space Flight Center Greenbelt, Maryland. 1965. Available online: https://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19660012530.pdf (accessed on 6 July 2020).
- Yen, T.-C.; Wang, K.-H.; Chen, J.-Y. Optimization Analysis of the N Policy M/G/1 Queue with Working Breakdowns. Symmetry 2020, 12, 583. [Google Scholar] [CrossRef]
- Shah, N.P. Entropy Maximisation and Queues with or without Balking. Ph.D. Thesis, School of Electrical Engineering and Computer Science, Faculty of Engineering and Informatics, University of Bradford, Bradford, UK, 2014. [Google Scholar]
- Singh, C.J.; Kaur, S.; Jain, M. Unreliable server retrial G-queue with bulk arrival, optional additional service and delayed repair. Int. J. Oper. Res. 2020, 38, 82–111. [Google Scholar] [CrossRef]
- She, R.; Liu, S.; Fan, P. Recognizing information feature variation: Message importance transfer measure and its applications in big data. Entropy 2018, 20, 401. [Google Scholar] [CrossRef]
- Giri, S.; Roy, R. On NACK-based rDWS algorithm for network coded broadcast. Entropy 2019, 21, 905. [Google Scholar] [CrossRef]
- Lin, W.; Wang, H.; Deng, Z.; Wang, K.; Zhou, X. State machine with tracking tree and traffic allocation scheme based on cumulative entropy for satellite network. Chin. J. Electron. 2020, 29, 185–189. [Google Scholar] [CrossRef]
- Bounkhel, M.; Tadj, L.; Hedjar, R. Steady-state analysis of a flexible Markovian queue with server breakdowns. Entropy 2019, 21, 259. [Google Scholar] [CrossRef]
- Luenberger, D.G.; Ye, Y. Introduction to Linear and Nonlinear Programming, 4th ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
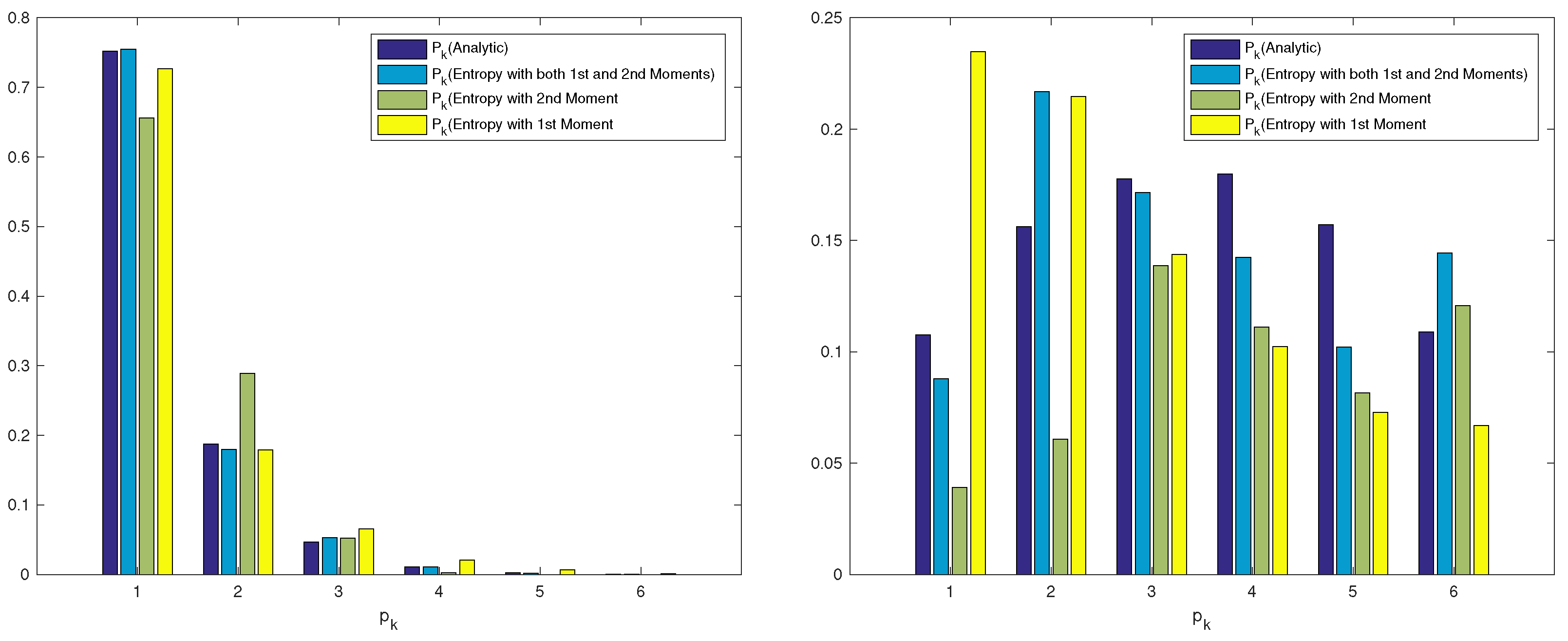
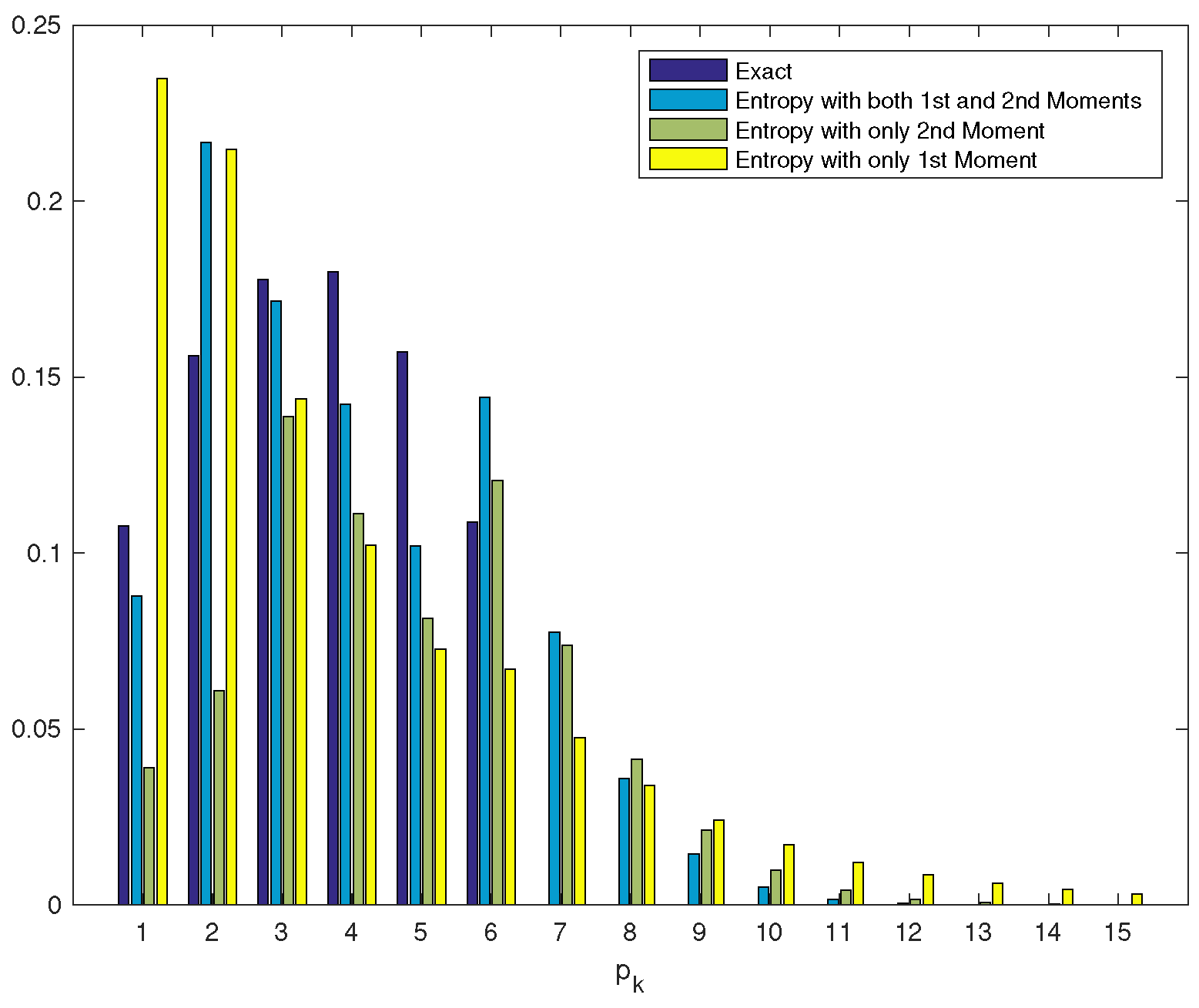



| Exact | Approx. 1 | Exact | Approx. 1 | |||
|---|---|---|---|---|---|---|
| 0.7519 | 0.7265 | 0.0338 | 0.1077 | 0.2349 | 1.1815 | |
| 0.1876 | 0.1794 | 0.0441 | 0.1561 | 0.2147 | 0.3748 | |
| 0.0465 | 0.0653 | 0.4049 | 0.1776 | 0.1438 | 0.1906 | |
| 0.0112 | 0.0206 | 0.8346 | 0.1799 | 0.1023 | 0.4316 | |
| 0.0024 | 0.0065 | 1.6986 | 0.1572 | 0.0727 | 0.5373 | |
| Average | 0.6032 | 0.5432 | ||||
| Exact | Appr. 1 | Appr. 2 | Exact | Appr. 1 | Appr. 2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.7519 | 0.7265 | 0.0338 | 0.6560 | 0.1275 | 0.1077 | 0.2349 | 1.1815 | 0.0391 | 0.6372 | |
| 0.1876 | 0.1794 | 0.0441 | 0.2892 | 0.5414 | 0.1561 | 0.2147 | 0.3748 | 0.0608 | 0.6108 | |
| 0.0465 | 0.0653 | 0.4049 | 0.0523 | 0.1237 | 0.1776 | 0.1438 | 0.1906 | 0.1387 | 0.2191 | |
| 0.0112 | 0.0206 | 0.8346 | 0.0025 | 0.7810 | 0.1799 | 0.1023 | 0.4316 | 0.1112 | 0.3821 | |
| 0.0024 | 0.0065 | 1.6986 | 0.0000 | 0.9858 | 0.1572 | 0.0727 | 0.5373 | 0.0815 | 0.4812 | |
| Average | 0.6032 | 0.5119 | 0.5432 | 0.4661 | ||||||
| Exact | Entropy 1 | Entropy 2 | Entropy | ||||
|---|---|---|---|---|---|---|---|
| 0.7519 | 0.7265 | 0.0338 | 0.6560 | 0.1275 | 0.7550 | 0.0040 | |
| 0.1876 | 0.1794 | 0.0441 | 0.2892 | 0.5414 | 0.1795 | 0.0431 | |
| 0.0465 | 0.0653 | 0.4049 | 0.0523 | 0.1237 | 0.0527 | 0.1324 | |
| 0.0112 | 0.0206 | 0.8346 | 0.0025 | 0.7810 | 0.0108 | 0.0346 | |
| 0.0024 | 0.0065 | 1.6986 | 0.0000 | 0.9858 | 0.0018 | 0.2421 | |
| Average | 0.6032 | 0.5119 | 0.0912 |
| Exact | Entropy 1 | Entropy 2 | Entropy | ||||
|---|---|---|---|---|---|---|---|
| 0.1077 | 0.2349 | 1.1815 | 0.0391 | 0.6372 | 0.0878 | 0.1843 | |
| 0.1561 | 0.2147 | 0.3748 | 0.0608 | 0.6108 | 0.2167 | 0.3881 | |
| 0.1776 | 0.1438 | 0.1906 | 0.1387 | 0.2191 | 0.1716 | 0.0341 | |
| 0.1799 | 0.1023 | 0.4316 | 0.1112 | 0.3821 | 0.1423 | 0.2090 | |
| 0.1572 | 0.0727 | 0.5373 | 0.0815 | 0.4812 | 0.1021 | 0.3503 | |
| Average | 0.5432 | 0.4661 | 0.2332 |
| Exact | Entropy 1 | Entropy 2 | Entropy 1&2 | |
|---|---|---|---|---|
| 0.2 | 0.5341 | 0.5393 | 0.4366 | 0.5352 |
| 0.4 | 0.2894 | 0.3826 | 0.2739 | 0.2673 |
| 0.6 | 0.1937 | 0.3189 | 0.1279 | 0.1618 |
| 0.8 | 0.1468 | 0.2794 | 0.1256 | 0.1169 |
| 1.0 | 0.1183 | 0.2486 | 0.0111 | 0.0949 |
| 1.2 | 0.0986 | 0.2219 | 0.1435 | 0.0821 |
| 1.4 | 0.0838 | 0.1974 | 0.1330 | 0.0733 |
| 1.6 | 0.0721 | 0.1744 | 0.0880 | 0.0660 |
| 1.8 | 0.0627 | 0.1523 | 0.0339 | 0.0597 |
| Exact | Entropy 1 | Entropy 2 | Entropy 1&2 | |
|---|---|---|---|---|
| 0.1 | 0.3312 | 0.4124 | 0.0136 | 0.3065 |
| 0.2 | 0.5429 | 0.5306 | 0.0126 | 0.5349 |
| 0.3 | 0.6756 | 0.6353 | 0.5493 | 0.6730 |
| 0.4 | 0.7526 | 0.7131 | 0.6338 | 0.7517 |
| 0.5 | 0.8009 | 0.7685 | 0.7000 | 0.8007 |
| 0.6 | 0.8337 | 0.8080 | 0.7520 | 0.8337 |
| 0.7 | 0.8573 | 0.8369 | 0.7925 | 0.8574 |
| 0.8 | 0.8751 | 0.8587 | 0.8237 | 0.8752 |
| 0.9 | 0.8889 | 0.8756 | 0.8478 | 0.8890 |
| 1 | 0.9000 | 0.8890 | 0.8665 | 0.9001 |
| Exact | Entropy 1 | Entropy 2 | Entropy 1&2 | |
|---|---|---|---|---|
| 4 | 0.7516 | 0.7422 | 0.6861 | 0.7586 |
| 5 | 0.7518 | 0.7299 | 0.6623 | 0.7558 |
| 6 | 0.7520 | 0.7241 | 0.6516 | 0.7544 |
| 7 | 0.7521 | 0.7210 | 0.6460 | 0.7536 |
| 8 | 0.7522 | 0.7190 | 0.6426 | 0.7531 |
| 9 | 0.7523 | 0.7177 | 0.6404 | 0.7528 |
| 10 | 0.7523 | 0.7168 | 0.6389 | 0.7525 |
| 11 | 0.7523 | 0.7161 | 0.6378 | 0.7524 |
| 12 | 0.7524 | 0.7155 | 0.6370 | 0.7523 |
| 13 | 0.7524 | 0.7151 | 0.6364 | 0.7522 |
| Exact | 0.7687 | 0.1863 | 0.0400 | ||||||
| Entropy 1 | 0.7582 | 0.1707 | 0.0575 | ||||||
| Entropy 2 | 0.7052 | 0.2625 | 0.0318 | ||||||
| Entropy 1&2 | 0.7701 | 0.1824 | 0.0438 | ||||||
| Exact | 0.7562 | 0.1876 | 0.0453 | 0.0097 | |||||
| Entropy 1 | 0.7348 | 0.1773 | 0.0633 | 0.0197 | |||||
| Entropy 2 | 0.6723 | 0.2810 | 0.0449 | 0.0017 | |||||
| Entropy 1&2 | 0.7582 | 0.1819 | 0.0500 | 0.0091 | |||||
| Exact | 0.7519 | 0.1876 | 0.0465 | 0.0112 | 0.0024 | ||||
| Entropy 1 | 0.7265 | 0.1794 | 0.0653 | 0.0206 | 0.0065 | ||||
| Entropy 2 | 0.6560 | 0.2892 | 0.0523 | 0.0025 | 0.0000 | ||||
| Entropy 1&2 | 0.7550 | 0.1795 | 0.0527 | 0.0108 | 0.0018 | ||||
| Exact | 0.7506 | 0.1876 | 0.0468 | 0.0116 | 0.0028 | 0.0006 | |||
| Entropy 1 | 0.7236 | 0.1801 | 0.0662 | 0.0209 | 0.0066 | 0.0021 | |||
| Entropy 2 | 0.6488 | 0.2927 | 0.0557 | 0.0028 | 0.0000 | 0.0000 | |||
| Entropy 1&2 | 0.7544 | 0.1777 | 0.0536 | 0.0117 | 0.0022 | 0.0003 | |||
| Exact | 0.7502 | 0.1875 | 0.0469 | 0.0117 | 0.0029 | 0.0007 | 0.0001 | ||
| Entropy 1 | 0.7224 | 0.1804 | 0.0665 | 0.0211 | 0.0067 | 0.0021 | 0.0007 | ||
| Entropy 2 | 0.6457 | 0.2941 | 0.0571 | 0.0030 | 0.0000 | 0.0000 | 0.0000 | ||
| Entropy 1&2 | 0.7545 | 0.1766 | 0.0540 | 0.0121 | 0.0023 | 0.0004 | 0.0001 | ||
| Exact | 0.7500 | 0.1875 | 0.0469 | 0.0117 | 0.0029 | 0.0007 | 0.0002 | 0.0000 | |
| Entropy 1 | 0.7219 | 0.1805 | 0.0668 | 0.0211 | 0.0067 | 0.0021 | 0.0007 | 0.0002 | |
| Entropy 2 | 0.6445 | 0.2947 | 0.0577 | 0.0031 | 0.0001 | 0.0000 | 0.0000 | 0.0000 | |
| Entropy 1&2 | 0.7547 | 0.1761 | 0.0541 | 0.0122 | 0.0024 | 0.0004 | 0.0001 | 0.0000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bounkhel, M.; Tadj, L.; Hedjar, R. Entropy Analysis of a Flexible Markovian Queue with Server Breakdowns. Entropy 2020, 22, 979. https://doi.org/10.3390/e22090979
Bounkhel M, Tadj L, Hedjar R. Entropy Analysis of a Flexible Markovian Queue with Server Breakdowns. Entropy. 2020; 22(9):979. https://doi.org/10.3390/e22090979
Chicago/Turabian StyleBounkhel, Messaoud, Lotfi Tadj, and Ramdane Hedjar. 2020. "Entropy Analysis of a Flexible Markovian Queue with Server Breakdowns" Entropy 22, no. 9: 979. https://doi.org/10.3390/e22090979
APA StyleBounkhel, M., Tadj, L., & Hedjar, R. (2020). Entropy Analysis of a Flexible Markovian Queue with Server Breakdowns. Entropy, 22(9), 979. https://doi.org/10.3390/e22090979





