Minimal Products of Coordinate and Momentum Uncertainties of High Orders: Significant and Weak High-Order Squeezing
Abstract
1. Introduction
2. Robertson–Schrödinger Relations with High-Order Moments for the Gaussian States
2.1. N = 2
2.2. N = 3, Homogeneous States
2.3. Arbitrary N, Vacuum Squeezed States
3. Fock States as Intelligent States
4. Nth Order Products in the Two-Term Even Fock Superpositions: General Formulas
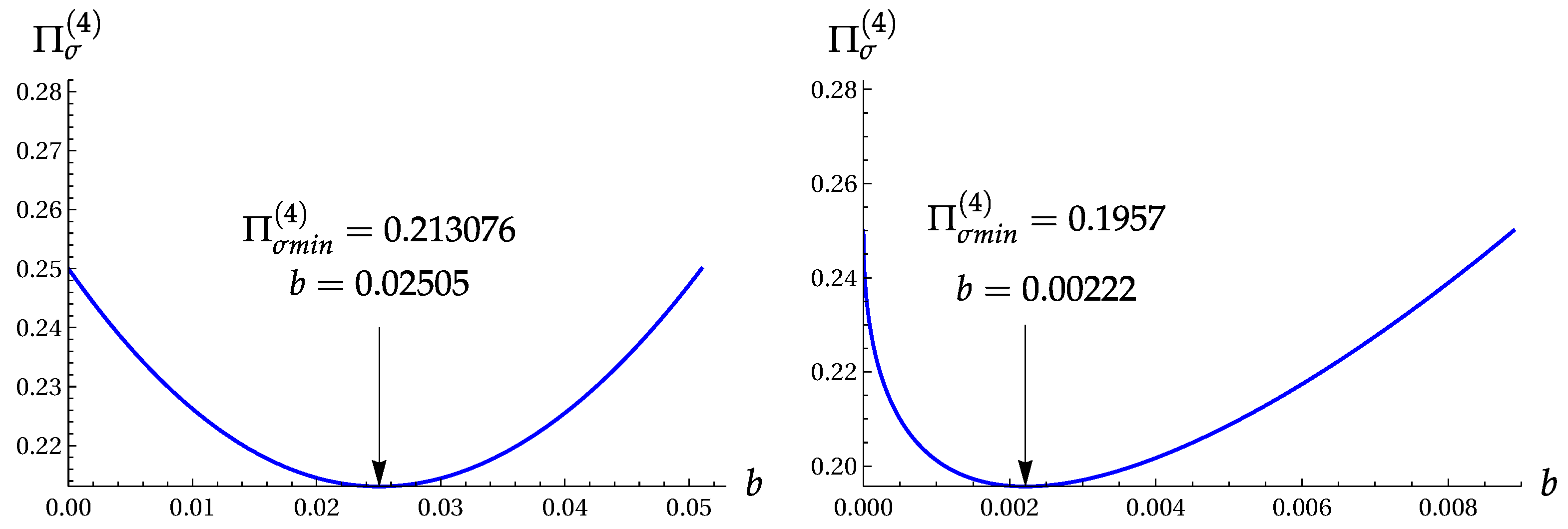
5. Fourth-Order Variance Products in States and
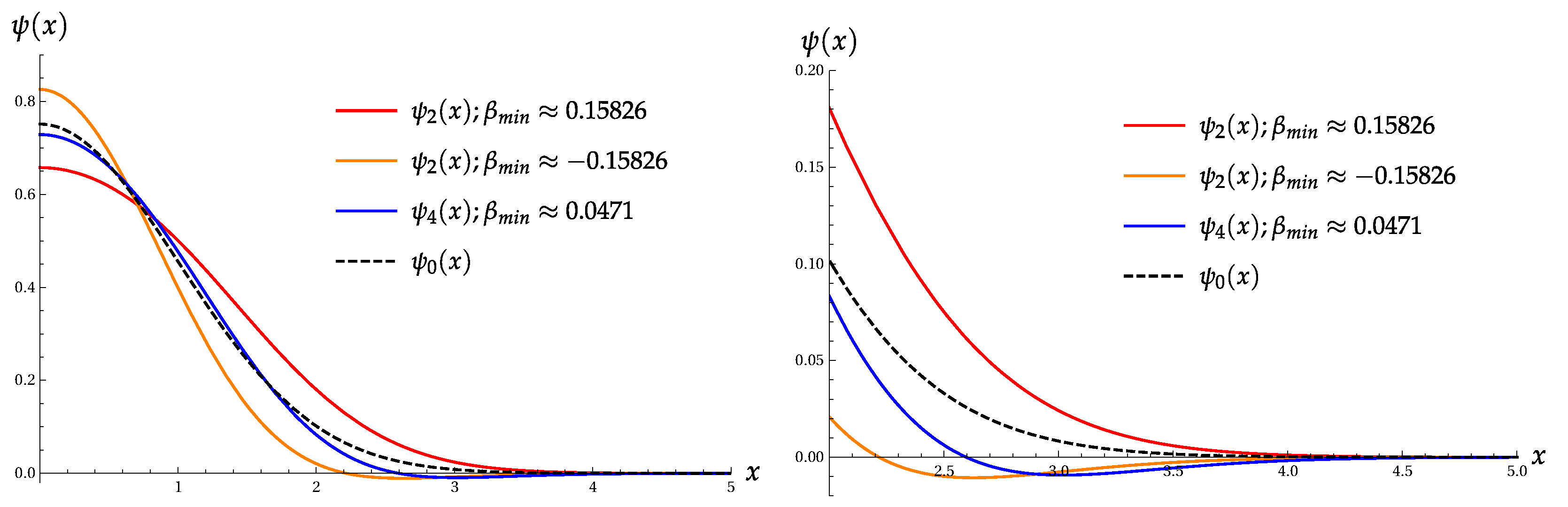
5.1. Superpositions of the Vacuum and Fourth Fock States
5.2. Superpositions of the Vacuum and Second Fock States
5.3. Superpositions of Three Even Fock States
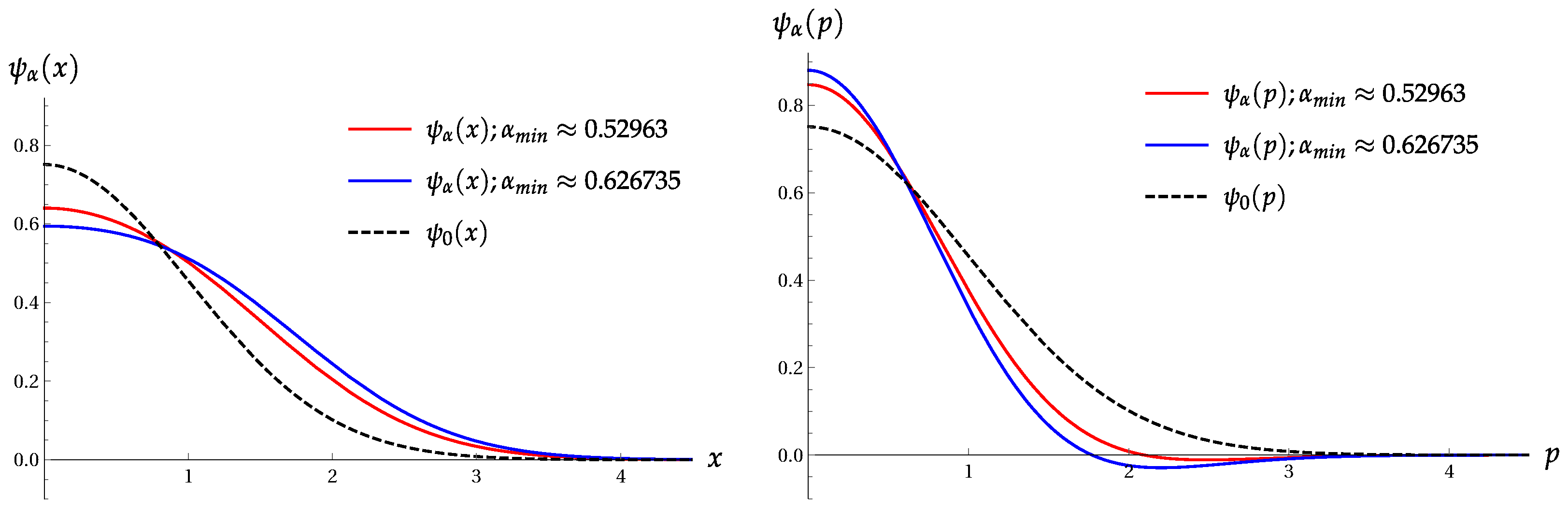
6. Superpositions of Coherent States
6.1. Two Coherent States
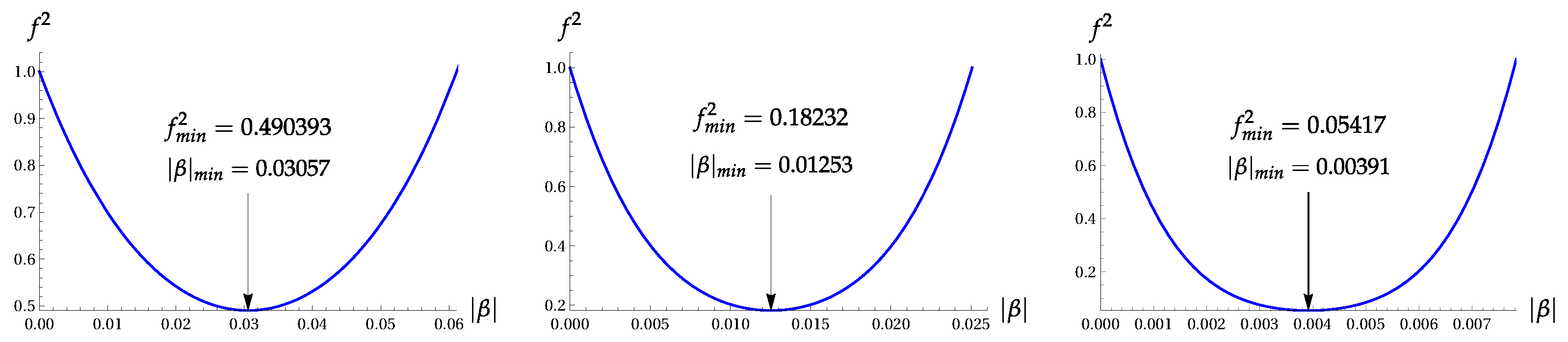
6.2. Superpositions of Four Coherent States (Orthogonal-Even Coherent States)
7. Sixth Order Products in Two-Term Superpositions of the Fock States
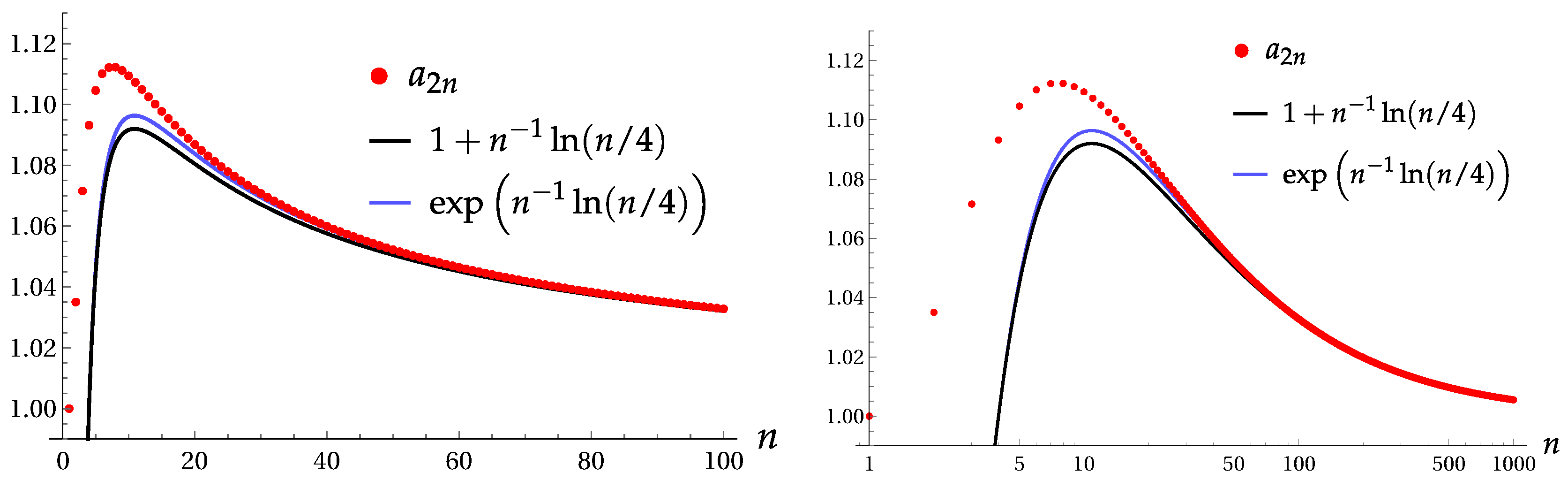
8. Asymptotic Values of High-Order Products in the Two-Term Fock Superpositions
9. Significant and Weak High-Order Squeezing
10. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Details of Calculations for the Gaussian States
Appendix B. Explicit Expressions for the Coefficients of Nth Order Moments in the Two-Term Even Fock Superpositions
References
- Kennard, E.H. Zur Quantenmechanik einfacher Bewegungstypen. Z. Phys. 1927, 44, 326–352. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Man’ko, V.I. Generalization of the uncertainty relations in quantum mechanics. In Invariants and the Evolution of Nonstationary Quantum Systems (Proceedings of Lebedev Physics Institute, Volume 183); Markov, M.A., Ed.; Nova Science: Commack, NY, USA, 1989; pp. 3–101. [Google Scholar]
- Cowling, M.G.; Price, J.F. Bandwidth versus time concentration: The Heisenberg–Pauli–Weyl inequality. SIAM J. Math. Anal. 1984, 15, 151–165. [Google Scholar] [CrossRef]
- Lynch, R.; Mavromatis, H.A. Nth (even)-order minimum uncertainty products. J. Math. Phys. 1990, 31, 1947–1951. [Google Scholar] [CrossRef]
- Shchukin, E.; van Loock, P. Higher-order Einstein-Podolsky-Rosen correlations and inseparability conditions for continuous variables. Phys. Rev. A 2016, 93, 032114. [Google Scholar] [CrossRef]
- Hach, E.E., III; Gerry, C.C. Four photon coherent states. Properties and generation. J. Mod. Opt. 1992, 39, 2501–2517. [Google Scholar] [CrossRef]
- Lynch, R. Simultaneous fourth-order squeezing of both quadrature components. Phys. Rev. A 1994, 49, 2800–2805. [Google Scholar] [CrossRef]
- Souza Silva, A.L.; Mizrahi, S.S.; Dodonov, V.V. Effect of phase-sensitive reservoir on the decoherence of pair-cat coherent states. J. Russ. Laser Res. 2001, 22, 534–544. [Google Scholar] [CrossRef]
- Zurek, W.H. Sub-Planck structure in phase space and its relevance for quantum decoherence. Nature 2001, 412, 712–717. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Lee, C.-W.; Nha, H.; Kaszlikowski, D. Quantum phase estimation using a multi-headed cat state. J. Opt. Soc. Am. B 2015, 32, 1186–1192. [Google Scholar] [CrossRef]
- Janszky, J.; Domokos, P.; Adam, P. Coherent states on a circle and quantum interference. Phys. Rev. A 1993, 48, 2213–2219. [Google Scholar] [CrossRef]
- Chountasis, S.; Vourdas, A. Weyl functions and their use in the study of quantum interference. Phys. Rev. A 1998, 58, 848–855. [Google Scholar] [CrossRef]
- Ragi, R.; Baseia, B.; Mizrahi, S.S. Non-classical properties of even circular states. J. Opt. B Quantum Semiclass. Opt. 2000, 2, 299–305. [Google Scholar] [CrossRef]
- Castaños, O.; López-Peña, R.; Man’ko, V.I. Crystallized Schrödinger cat states. J. Russ. Laser Res. 1995, 16, 477–525. [Google Scholar] [CrossRef]
- Dodonov, V.V. ‘Nonclassical’ states in quantum optics: A ‘squeezed’ review of the first 75 years. J. Opt. B Quantum Semiclass. Opt. 2002, 4, R1–R33. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Valverde, C.; Souza, L.S.; Baseia, B. Decoherence of odd compass states in the phase-sensitive amplifying/dissipating environment. Ann. Phys. 2016, 371, 296–312. [Google Scholar] [CrossRef]
- Rath, B. An interesting new revelation on simultaneous higher order squeezing in an electro-magnetic field. Prog. Theor. Phys. 2001, 105, 697–705. [Google Scholar] [CrossRef][Green Version]
- Kumar, P.; Kumar, R. Simultaneous higher-order Hong and Mandel’s squeezing of both quadrature components in orthogonal even coherent state. Optik 2013, 124, 2229–2233. [Google Scholar] [CrossRef]
- Schrödinger, E. Zum Heisenbergschen Unschärfeprinzip. Sitzungsberichte der Preussischen Akademie der Wissenschaften. Physikalisch-Mathematische Klasse; Walter de Gruyter: Berlin, Germany, 1930; pp. 296–303. [Google Scholar]
- Robertson, H.P. A general formulation of the uncertainty principle and its classical interpretation. Phys. Rev. 1930, 35, 667. [Google Scholar]
- Aragone, C.; Guerri, G.; Salamó, S.; Tani, J.L. Intelligent spin states. J. Phys. A Math. Nucl. Gen. 1974, 7, L149–L151. [Google Scholar] [CrossRef]
- Aragone, C.; Chalbaud, E.; Salamó, S. On intelligent spin states. J. Math. Phys. 1976, 17, 1963–1971. [Google Scholar] [CrossRef]
- Vanden Berghe, G.; De Meyer, H. On the existence of intelligent states associated with the non-compact group SU(1,l). J. Phys. A Math. Gen. 1978, 11, 1569–1578. [Google Scholar] [CrossRef]
- Adam, P.; Janszky, J.; Vinogradov, A.V. Amplitude squeezed and number-phase intelligent states via coherent state superposition. Phys. Lett. A 1991, 160, 506–510. [Google Scholar] [CrossRef]
- El Kinani, A.H.; Daoud, M. Generalized intelligent states for an arbitrary quantum system. J. Phys. A Math. Gen. 2001, 34, 5373–5387. [Google Scholar] [CrossRef]
- Milks, M.M.; de Guise, H. Polynomial intelligent states. J. Opt. B Quantum Semiclass. Opt. 2005, 7, S622–S627. [Google Scholar] [CrossRef]
- Przanowski, M.; García-Compeán, H.; Tosiek, J.; Turrubiates, F.J. Uncertainty relations in quantum optics. Is the photon intelligent? Ann. Phys. 2016, 373, 123–144. [Google Scholar] [CrossRef]
- Trifonov, D.A. Generalized intelligent states and squeezing. J. Math. Phys. 1994, 35, 2297–2308. [Google Scholar] [CrossRef]
- Trifonov, D.A. Robertson intelligent states. J. Phys. A Math. Gen. 1997, 30, 5941–5957. [Google Scholar] [CrossRef]
- Trifonov, D.A. Exact solutions for the general nonstationary oscillator with a singular perturbation. J. Phys. A Math. Gen. 1999, 32, 3649–3661. [Google Scholar] [CrossRef]
- Brif, C.; Mann, A. Nonclassical interferometry with intelligent light. Phys. Rev. A 1996, 54, 4505–4518. [Google Scholar] [CrossRef]
- Gerry, C.C.; Gou, S.-C.; Steinbach, J. Generation of motional SU(1,1) intelligent states of a trapped ion. Phys. Rev. A 1997, 55, 630–635. [Google Scholar] [CrossRef]
- Peřinová, V.; Lukš, A.; Křepelka, J. Intelligent states in SU(2) and SU(1, 1) interferometry. J. Opt. B Quantum Semiclass. Opt. 2000, 2, 81–89. [Google Scholar] [CrossRef]
- Messina, A.; Maniscalco, S.; Napoli, A. Interaction of bimodal fields with few-level atoms in cavities and traps. J. Mod. Opt. 2003, 50, 1–49. [Google Scholar] [CrossRef]
- Řeháček, J.; Bouchal, Z.; Čelechovský, R.; Hradil, Z.; Sánchez-Soto, L.L. Experimental test of uncertainty relations for quantum mechanics on a circle. Phys. Rev. A 2008, 77, 032110. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Kurmyshev, E.V.; Man’ko, V.I. Generalized uncertainty relation and correlated coherent states. Phys. Lett. A 1980, 79, 150–152. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Malkin, I.A.; Man‘ko, V.I. Even and odd coherent states and excitations of a singular oscillator. Physica 1974, 72, 597–615. [Google Scholar] [CrossRef]
- Bužek, V.; Knight, P.L. Quantum interference, superposition states of light, and nonclassical effects. In Progress in Optics, Volume XXXIV; Wolf, E., Ed.; North Holland: Amsterdam, The Netherlands, 1995; pp. 1–158. [Google Scholar]
- Man’ko, V.I. Even and odd coherent states and tomographic representation of quantum mechanics and quantum optics. In Theory of Nonclassical States of Light; Dodonov, V.V., Man’ko, V.I., Eds.; Taylor & Francis: London, UK, 2003; pp. 219–240. [Google Scholar]
- Hong, C.K.; Mandel, L. Generation of higher-order squeezing of quantum electromagnetic field. Phys. Rev. A 1985, 32, 974–982. [Google Scholar] [CrossRef]
- Hillery, M. Amplitude-squared squeezing of the electromagnetic field. Phys. Rev. A 1987, 36, 3796–3802. [Google Scholar] [CrossRef]
- Zhang, Z.M.; Xu, L.; Cai, J.L.; Li, F.L. A new kind of higher-order squeezing of radiation field. Phys. Lett. A 1990, 150, 27–30. [Google Scholar] [CrossRef]
- Nagel, B. Higher power squeezed states, Jacobi matrices, and the Hamburger moment problem. arXiv 1997, arXiv:quant-ph/9711028. [Google Scholar]
- Górska, K.; Horzela, A.; Szafraniec, F.H. Squeezing of arbitrary order: The ups and downs. Proc. R. Soc. A 2014, 470, 20140205. [Google Scholar] [CrossRef]
- Bužek, V.; Vidiella-Barranco, A.; Knight, P.L. Superpositions of coherent states: Squeezing and dissipation. Phys. Rev. A 1992, 45, 6570–6585. [Google Scholar] [CrossRef] [PubMed]
- Du, S.-D.; Gong, C.-D. Squeezing of the kth power of the field amplitude. Phys. Lett. A 1992, 168, 296–300. [Google Scholar] [CrossRef]
- Gerry, C.C. Nonclassical properties of even and odd coherent states. J. Mod. Opt. 1993, 40, 1053–1071. [Google Scholar] [CrossRef]
- Fan, H.; Zhang, Z. General expressions of higher-order squeezing for even and odd coherent states. Phys. Lett. A 1993, 179, 175–178. [Google Scholar] [CrossRef]
- Prakash, H.; Kumar, P. Fourth-order squeezing in superposed coherent states. Acta Phys. Polon. B 2003, 34, 2769–2774. [Google Scholar]
- Ahmad, M.A.; Azam, S.; Aslam, S.; Bukhari, S.H.; Jamil, A.; Mustafa, F.; Khan, S.N. Higher order squeezing as a measure of nonclassicality. Optik 2016, 127, 2992–2995. [Google Scholar] [CrossRef]
- Prakash, H.; Kumar, R.; Kumar, P. Higher-order Hong–Mandel’s squeezing in superposed coherent states. Opt. Commun. 2011, 284, 289–293. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, R.; Prakash, H. Simultaneous higher-order Hong–Mandel’s squeezing and higher-order sub-Poissonian photon statistics in superposed coherent states. Optik 2016, 127, 4826–4830. [Google Scholar] [CrossRef]
- Kumar, P.; Kumar, R.; Prakash, H. Enhancement of the Hong–Mandel higher-order squeezing and amplitude odd-power squeezing in even coherent state by its superposition with vacuum state. Acta Phys. Polon. A 2017, 131, 1485–1490. [Google Scholar] [CrossRef]
- Duc, T.M.; Dinh, D.H.; Dat, T.Q. Even and odd charge coherent states: Higher-order nonclassical properties and generation scheme. Int. J. Theor. Phys. 2016, 55, 3027–3040. [Google Scholar] [CrossRef]
- Duc, T.M.; Dinh, D.H.; Dat, T.Q. Higher-order nonclassical properties of nonlinear charge pair cat states. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 025402. [Google Scholar] [CrossRef]
- Marian, P. Higher-order squeezing and photon statistics for squeezed thermal states. Phys. Rev. A 1992, 45, 2044–2051. [Google Scholar] [CrossRef] [PubMed]
- Marian, P. Higher-order squeezing properties and correlation functions for squeezed number states. Phys. Rev. A 1991, 44, 3325–3330. [Google Scholar] [CrossRef] [PubMed]
- D’Ariano, G.; Rasetti, M. Non-Gaussian multiphoton squeezed states. Phys. Rev. D 1987, 35, 1239–1247. [Google Scholar] [CrossRef]
- Tombesi, P.; Mecozzi, A. Four-photon squeezed states: An exactly solvable model. Phys. Rev. A 1988, 37, 4778–4784. [Google Scholar] [CrossRef]
- Gong, J.J.; Aravind, P.K. Higher-order squeezing in three- and four-wave mixing processes with loss. Phys. Rev. A 1992, 46, 1586–1593. [Google Scholar] [CrossRef]
- Li, X.-Z.; Su, B.-X.; Chai, L. Higher-order squeezing of quantum electromagnetic fields and higher-order uncertainty relations in two-mode squeezed states. Chin. Phys. 2004, 13, 2058–2063. [Google Scholar]
- Duc, T.M.; Noh, J. Higher-order properties of photon-added coherent states. Opt. Commun. 2008, 281, 2842–2848. [Google Scholar] [CrossRef]
- Aeineh, N.; Tavassoly, M.K. Higher-orders of squeezing, sub-Poissonian statistics and anti-bunching of deformed photon-added coherent states. Rep. Math. Phys. 2015, 76, 75–89. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Renó, M.B. Nonclassical properties of ‘semi-coherent’ quantum states. J. Phys. A Math. Theor. 2006, 39, 7411–7422. [Google Scholar] [CrossRef]
- Piroozi, E.; Tavassoly, M.K. Nonlinear semi-coherent states, their nonclassical features and phase properties. J. Phys. A Math. Theor. 2012, 45, 135301. [Google Scholar] [CrossRef]
- Garcia, P.; Bermejo, F.J.; Santoro, J.; Sainz, L. Sub-Poissonian photon statistics and higher-order squeezing in the light amplifier with input binomial states. J. Mod. Opt. 1987, 34, 997–1005. [Google Scholar] [CrossRef]
- Mandal, K.; Alam, N.; Verma, A.; Pathak, A.; Banerji, J. Generalized binomial state: Nonclassical features observed through various witnesses and a quantifier of nonclassicality. Opt. Commun. 2019, 445, 193–203. [Google Scholar] [CrossRef]
- Giri, D.K.; Gupta, P.S. nth-order amplitude squeezing effects of radiation in multiphoton processes. Int. J. Mod. Phys. B 2006, 20, 2265–2281. [Google Scholar] [CrossRef]
- Dodonov, V.V. Comparing energy difference and fidelity of quantum states. J. Russ. Laser Res. 2011, 32, 412–421. [Google Scholar] [CrossRef][Green Version]
- Dodonov, V.V. Upper bounds on the relative energy difference of pure and mixed Gaussian states with a fixed fidelity. J. Phys. A Math. Theor. 2012, 45, 032002. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Horovits, M.B. How different can pure squeezed states with a given fidelity be? Phys. Scr. T 2012, 147, 014009. [Google Scholar] [CrossRef]
- Bina, M.; Mandarino, A.; Olivares, S.; Paris, M.G.A. Drawbacks of the use of fidelity to assess quantum resources. Phys. Rev. A 2014, 89, 012305. [Google Scholar] [CrossRef]
- Mandarino, A.; Bina, M.; Olivares, S.; Paris, M.G.A. About the use of fidelity in continuous variable systems. Int. J. Quantum Inf. 2014, 12, 1461015. [Google Scholar] [CrossRef]
- Mandarino, A.; Bina, M.; Porto, C.; Cialdi, S.; Olivares, S.; Paris, M.G.A. Assessing the significance of fidelity as a figure of merit in quantum state reconstruction of discrete and continuous-variable systems. Phys. Rev. A 2016, 93, 062118. [Google Scholar] [CrossRef]
- Rodríguez, E.B.; Aguilar, L.M.A. A survey of the concept of disturbance in quantum mechanics. Entropy 2019, 21, 142. [Google Scholar] [CrossRef]
- Robertson, H.P. An indeterminacy relation for several observables and its classical interpretation. Phys. Rev. 1934, 46, 794–801. [Google Scholar] [CrossRef]
- Simon, R.; Mukunda, N.; Dutta, B. Quantum-noise matrix for multimode systems: U(n) invariance, squeezing, and normal forms. Phys. Rev. A 1994, 49, 1567–1583. [Google Scholar] [CrossRef] [PubMed]
- Sudarshan, E.C.G.; Chiu, C.B.; Bhamathi, G. Generalized uncertainty relations and characteristic invariants for the multimode states. Phys. Rev. A 1995, 52, 43–54. [Google Scholar] [CrossRef]
- Wünsche, A. Higher-order uncertainty relations. J. Mod. Opt. 2006, 53, 931–968. [Google Scholar] [CrossRef]
- Kechrimparis, S.; Weigert, S. Preparational uncertainty relations for N continuous variables. Mathematics 2016, 4, 49. [Google Scholar] [CrossRef]
- Qin, H.-H.; Fei, S.-M.; Li-Jost, X. Multi-observable uncertainty relations in product form of variances. Sci. Rep. 2016, 6, 31192. [Google Scholar] [CrossRef]
- Dodonov, V.V. Variance uncertainty relations without covariances for three and four observables. Phys. Rev. A 2018, 97, 022105. [Google Scholar] [CrossRef]
- Zhang, D.; Li, C.; Zhang, Z.; Zhang, Y.; Zhang, Y.; Xiao, M. Enhanced intensity-difference squeezing via energy-level modulations in hot atomic media. Phys. Rev. A 2017, 96, 043847. [Google Scholar] [CrossRef]
- Li, C.; Jiang, Z.; Zhang, Y.; Zhang, Z.; Wen, F.; Chen, H.; Zhang, Y.; Xiao, M. Controlled correlation and squeezing in Pr3+: Y2SiO5 to yield correlated light beams. Phys. Rev. Appl. 2017, 7, 014023. [Google Scholar] [CrossRef]
- Dodonov, V.V. Purity- and entropy-bounded uncertainty relations for mixed quantum states. J. Opt. B Quantum Semiclass. Opt. 2002, 4, S98–S108. [Google Scholar] [CrossRef]
- Mandilara, A.; Karpov, E.; Cerf, N.J. Purity- and Gaussianity-bounded uncertainty relations. J. Phys. A Math. Theor. 2014, 47, 045302. [Google Scholar] [CrossRef]
- Man’ko, V.I.; Marmo, G.; Simoni, A.; Ventriglia, F. Two-mode optical tomograms: A possible experimental check of the Robertson uncertainty relations. Phys. Scr. 2011, T147, 014021. [Google Scholar] [CrossRef]
- Bellini, M.; Coelho, A.S.; Filippov, S.N.; Man’ko, V.I.; Zavatta, A. Towards higher precision and operational use of optical homodyne tomograms. Phys. Rev. A 2012, 85, 052129. [Google Scholar] [CrossRef]
- Wang, K.; Zhan, X.; Bian, Z.; Li, J.; Zhang, Y.; Xue, P. Experimental investigation of the stronger uncertainty relations for all incompatible observables. Phys. Rev. A 2016, 93, 052108. [Google Scholar] [CrossRef]
- Ma, W.; Ma, Z.; Wang, H.; Chen, Z.; Liu, Y.; Kong, F.; Li, Z.; Peng, X.; Shi, M.; Shi, F.; et al. Experimental test of Heisenberg’s measurement uncertainty relation based on statistical distances. Phys. Rev. Lett. 2016, 116, 160405. [Google Scholar] [CrossRef]
- Ma, W.; Chen, B.; Liu, Y.; Wang, M.; Ye, X.; Kong, F.; Shi, F.; Fei, S.M.; Du, J. Experimental demonstration of uncertainty relations for the triple components of angular momentum. Phys. Rev. Lett. 2017, 118, 180402. [Google Scholar] [CrossRef]
- Bong, K.-W.; Tischler, N.; Patel, R.B.; Wollmann, S.; Pryde, G.J.; Hall, M.J.W. Strong unitary and overlap uncertainty relations: Theory and experiment. Phys. Rev. Lett. 2018, 120, 230402. [Google Scholar] [CrossRef]
- Fan, B.; Wang, K.; Xiao, L.; Xue, P. Experimental test of a stronger multiobservable uncertainty relation. Phys. Rev. A 2018, 98, 032118. [Google Scholar] [CrossRef]
- Chen, Z.-X.; Wang, H.; Li, J.-L.; Song, Q.-C.; Qiao, C.-F. Tight N-observable uncertainty relations and their experimental demonstrations. Sci. Rep. 2019, 9, 5687. [Google Scholar] [CrossRef]
- Wang, Z.-W.; Huang, Y.-F.; Ren, X.-F.; Zhang, Y.-S.; Guo, G.-C. Experimental entanglement quantification and verification via uncertainty relations. Europhys. Lett. 2007, 78, 40002. [Google Scholar] [CrossRef]
- Li, K.; Cai, Y.; Wu, J.; Liu, Y.; Xiong, S.; Li, Y.; Zhang, Y. Three-Body Topology Entanglement Generation via a Six-Wave Mixing: Competing and Coexisting of Linear and Nonlinear Optics Responses in Triphoton Temporal Correlation. Adv. Quantum Technol. 2020, 3, 1900119. [Google Scholar] [CrossRef]
- Liu, Y.; Li, K.; Li, W.; Li, S.; Cai, Y.; Zhang, Y. Dressing-controlled quantum steering in energy-level cascaded parametric amplified four-wave mixing processes. Adv. Quantum Technol. 2020, 3, 2000029. [Google Scholar] [CrossRef]
- Gradshtein, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 7th ed.; Academic: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series. Volume 2. Special Functions; Taylor & Francis: London, UK, 2002. [Google Scholar]





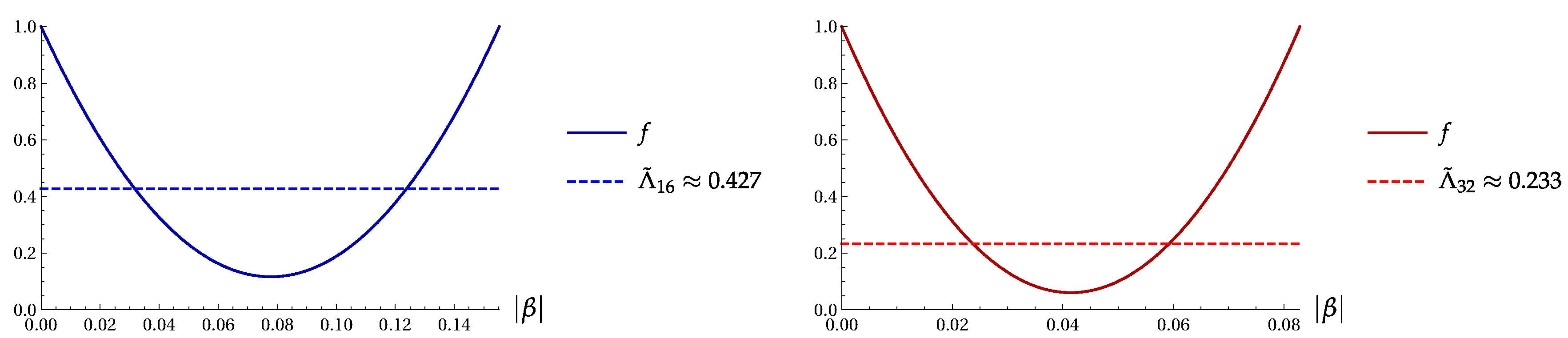
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Citeli de Freitas, M.; Dantas Meireles, V.; Dodonov, V.V. Minimal Products of Coordinate and Momentum Uncertainties of High Orders: Significant and Weak High-Order Squeezing. Entropy 2020, 22, 980. https://doi.org/10.3390/e22090980
Citeli de Freitas M, Dantas Meireles V, Dodonov VV. Minimal Products of Coordinate and Momentum Uncertainties of High Orders: Significant and Weak High-Order Squeezing. Entropy. 2020; 22(9):980. https://doi.org/10.3390/e22090980
Chicago/Turabian StyleCiteli de Freitas, Miguel, Vitor Dantas Meireles, and Viktor V. Dodonov. 2020. "Minimal Products of Coordinate and Momentum Uncertainties of High Orders: Significant and Weak High-Order Squeezing" Entropy 22, no. 9: 980. https://doi.org/10.3390/e22090980
APA StyleCiteli de Freitas, M., Dantas Meireles, V., & Dodonov, V. V. (2020). Minimal Products of Coordinate and Momentum Uncertainties of High Orders: Significant and Weak High-Order Squeezing. Entropy, 22(9), 980. https://doi.org/10.3390/e22090980





