A Novel Perspective of the Kalman Filter from the Rényi Entropy
Abstract
:1. Introduction
2. The Connection between the Kalman Filter and the Temporal Derivative of the Rényi Entropy
2.1. Rényi Entropy
2.2. Kalman Filter
2.3. Derivation of the Kalman Filter
2.4. The Temporal Derivative of the Rényi Entropy and the Kalman Filter Gain
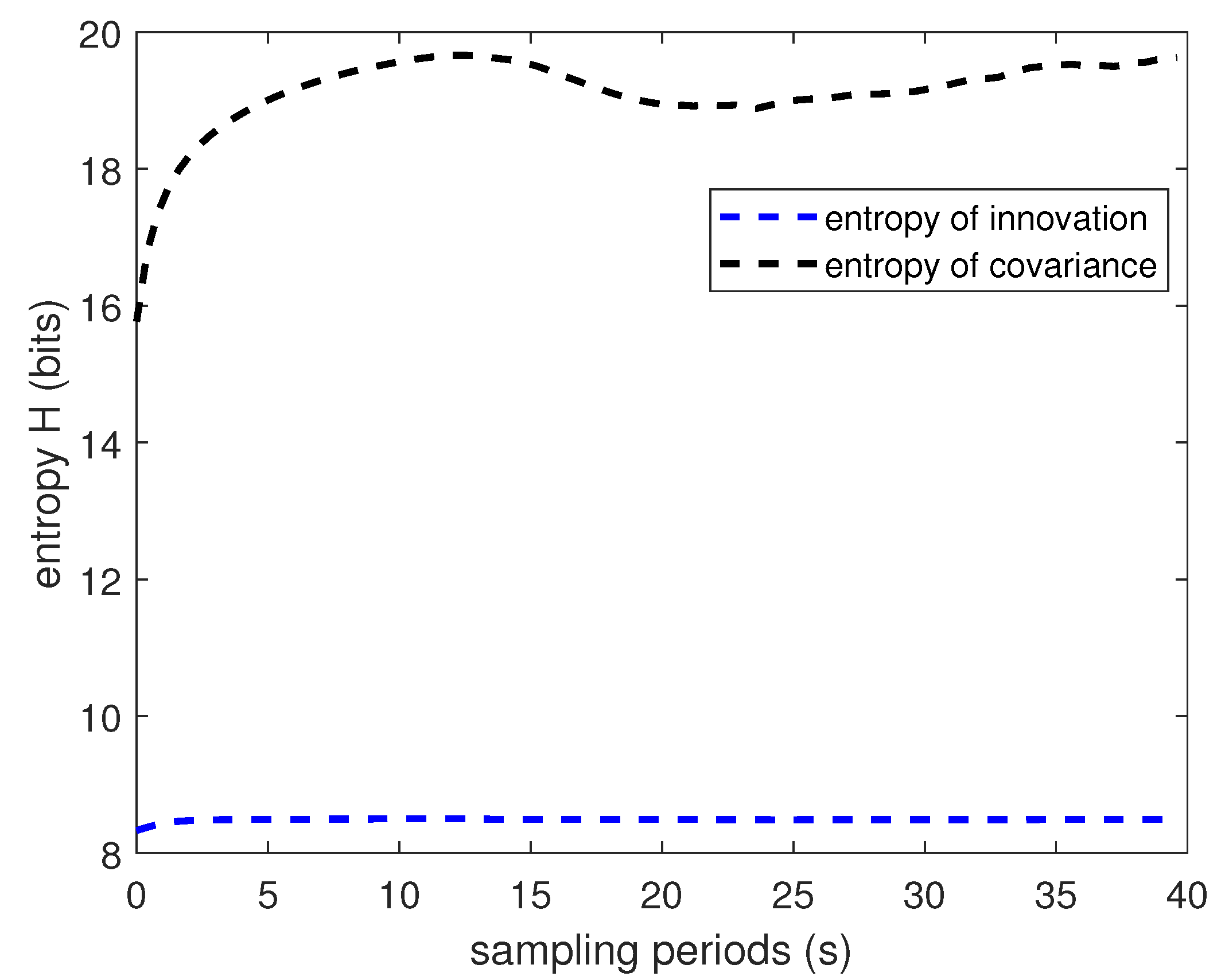
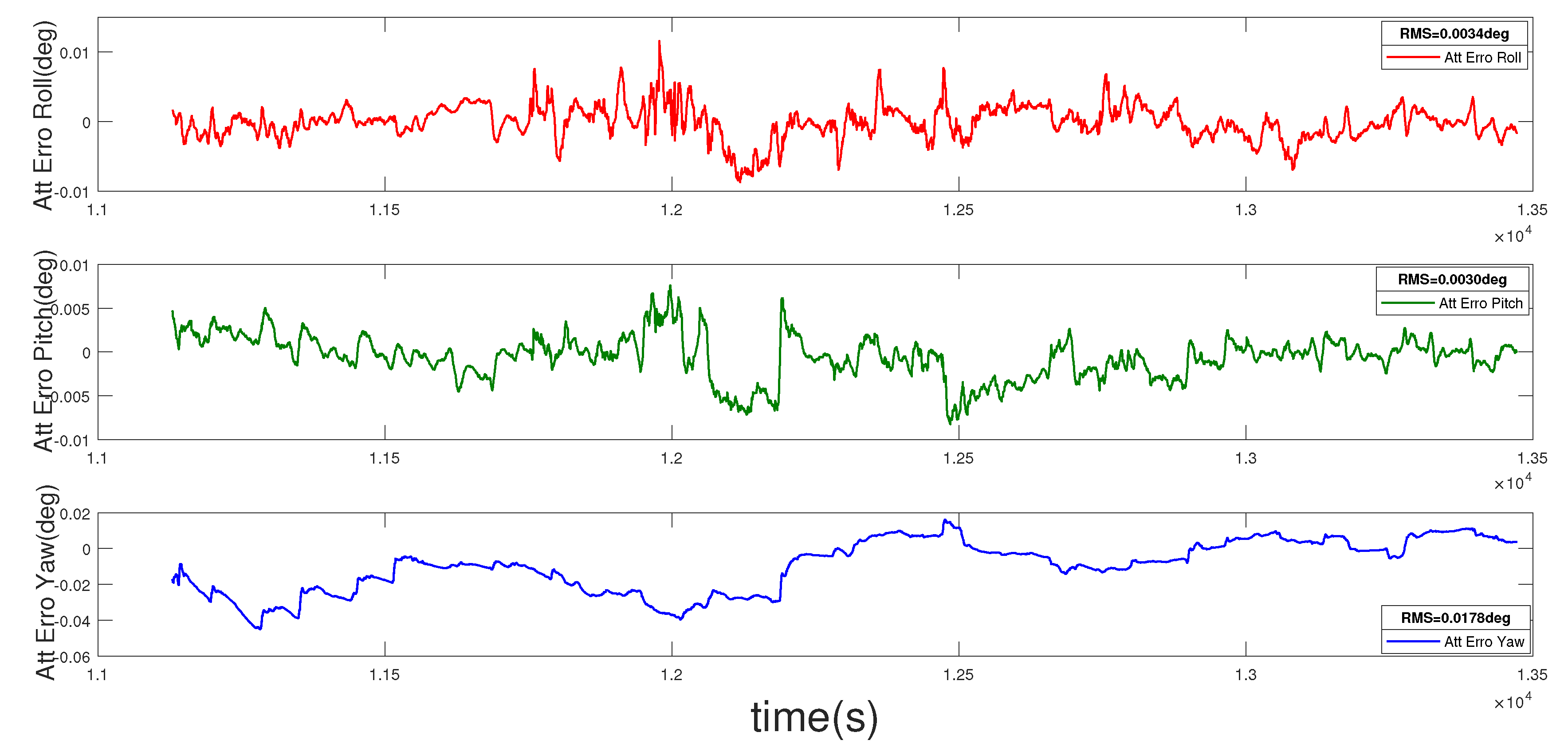
3. Simulations and Analysis
3.1. Falling Body Tracking
3.2. Practical Integrated Navigation
4. Conclusions and Final Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Principe, J.C. Information Theoretic Learning: Renyi’s Entropy and Kernel Perspectives; Springer Science & Business Media: Berlin, Germany, 2010. [Google Scholar]
- He, R.; Hu, B.; Yuan, X.; Wang, L. Robust Recognition via Information Theoretic Learning; Springer International Publishing: Berlin, Germany, 2014. [Google Scholar]
- Rényi, A. On measures of entropy and information. In Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability, Berkeley, CA, USA, 20 June–30 July 1961. [Google Scholar]
- Liang, X.S. Entropy evolution and uncertainty estimation with dynamical systems. Entropy 2014, 16, 3605–3634. [Google Scholar] [CrossRef]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- DeMars, K.J. Nonlinear Orbit Uncertainty Prediction and Rectification for Space Situational Awareness. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2010. [Google Scholar]
- DeMars, K.J.; Bishop, R.H.; Jah, M.K. Entropy-based approach for uncertainty propagation of nonlinear dynamical systems. J. Guid. Control. Dyn. 2013, 36, 1047–1057. [Google Scholar] [CrossRef]
- Kim, H.; Liu, B.; Goh, C.Y.; Lee, S.; Myung, H. Robust vehicle localization using entropy-weighted particle filter-based data fusion of vertical and road intensity information for a large scale urban area. IEEE Robot. Autom. Lett. 2017, 2, 1518–1524. [Google Scholar] [CrossRef]
- Zhang, J.; Du, L.; Ren, M.; Hou, G. Minimum error entropy filter for fault detection of networked control systems. Entropy 2012, 14, 505–516. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Hou, C. UKF based nonlinear filtering using minimum entropy criterion. IEEE Trans. Signal Process. 2013, 61, 4988–4999. [Google Scholar] [CrossRef]
- Julier, S.; Uhlmann, J.; Durrant-Whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control 2000, 45, 477–482. [Google Scholar] [CrossRef] [Green Version]
- Contreras-Reyes, J.E.; Cortés, D.D. Bounds on rényi and shannon entropies for finite mixtures of multivariate skew-normal distributions: Application to swordfish (xiphias gladius linnaeus). Entropy 2016, 18, 382. [Google Scholar] [CrossRef]
- Ren, M.; Zhang, J.; Fang, F.; Hou, G.; Xu, J. Improved minimum entropy filtering for continuous nonlinear non-Gaussian systems using a generalized density evolution equation. Entropy 2013, 15, 2510–2523. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q. Performance enhanced Kalman filter design for non-Gaussian stochastic systems with data-based minimum entropy optimisation. AIMS Electron. Electr. Eng. 2019, 3, 382. [Google Scholar] [CrossRef]
- Chen, B.; Dang, L.; Gu, Y.; Zheng, N.; Príncipe, J.C. Minimum error entropy Kalman filter. IEEE Trans. Syst. Man Cybern. Syst. 2019. [Google Scholar] [CrossRef] [Green Version]
- Gultekin, S.; Paisley, J. Nonlinear Kalman filtering with divergence minimization. IEEE Trans. Signal Process. 2017, 65, 6319–6331. [Google Scholar] [CrossRef] [Green Version]
- Darling, J.E.; DeMars, K.J. Minimization of the kullback–leibler divergence for nonlinear estimation. J. Guid. Control Dyn. 2017, 40, 1739–1748. [Google Scholar] [CrossRef]
- Morelande, M.R.; Garcia-Fernandez, A.F. Analysis of Kalman filter approximations for nonlinear measurements. IEEE Trans. Signal Process. 2013, 61, 5477–5484. [Google Scholar] [CrossRef]
- Raitoharju, M.; García-Fernández, Á.F.; Piché, R. Kullback–Leibler divergence approach to partitioned update Kalman filter. Signal Process. 2017, 130, 289–298. [Google Scholar] [CrossRef] [Green Version]
- Hu, E.; Deng, Z.; Xu, Q.; Yin, L.; Liu, W. Relative entropy-based Kalman filter for seamless indoor/outdoor multi-source fusion positioning with INS/TC-OFDM/GNSS. Clust. Comput. 2019, 22, 8351–8361. [Google Scholar] [CrossRef]
- Yu, W.; Peng, J.; Zhang, X.; Li, S.; Liu, W. An adaptive unscented particle filter algorithm through relative entropy for mobile robot self-localization. Math. Probl. Eng. 2013. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef] [Green Version]
- Kiani, M.; Barzegar, A.; Pourtakdoust, S.H. Entropy-based adaptive attitude estimation. Acta Astronaut. 2018, 144, 271–282. [Google Scholar] [CrossRef]
- Giffin, A.; Urniezius, R. The Kalman filter revisited using maximum relative entropy. Entropy 2014, 16, 1047–1069. [Google Scholar] [CrossRef]
- Chen, B.; Liu, X.; Zhao, H.; Principe, J.C. Maximum correntropy Kalman filter. Automatica 2017, 76, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Xing, L.; Liang, J.; Zheng, N.; Principe, J.C. Steady-state mean-square error analysis for adaptive filtering under the maximum correntropy criterion. IEEE Signal Process. Lett. 2014, 21, 880–884. [Google Scholar]
- Gongmin, Y.; Jun, W. Lectures on Strapdown Inertial Navigation Algorithm and Integrated Navigation Principles; Northwestern Polytechnical University Press: Xi’an, China, 2019. [Google Scholar]
- Kumari, L.; Padma Raju, K. Application of Extended Kalman filter for a Free Falling body towards Earth. IJACSA Ed. 2011, 2, 4. [Google Scholar] [CrossRef]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Guo, C.; You, S.; Liu, J. A Novel Perspective of the Kalman Filter from the Rényi Entropy. Entropy 2020, 22, 982. https://doi.org/10.3390/e22090982
Luo Y, Guo C, You S, Liu J. A Novel Perspective of the Kalman Filter from the Rényi Entropy. Entropy. 2020; 22(9):982. https://doi.org/10.3390/e22090982
Chicago/Turabian StyleLuo, Yarong, Chi Guo, Shengyong You, and Jingnan Liu. 2020. "A Novel Perspective of the Kalman Filter from the Rényi Entropy" Entropy 22, no. 9: 982. https://doi.org/10.3390/e22090982
APA StyleLuo, Y., Guo, C., You, S., & Liu, J. (2020). A Novel Perspective of the Kalman Filter from the Rényi Entropy. Entropy, 22(9), 982. https://doi.org/10.3390/e22090982





