Exergy Analysis of a Bio-System: Soil–Plant Interaction
Abstract
:1. Introduction
- Evaluate the exergy performance of the bio-system (plant–soil system) by overall exergy efficiency.
- Identify the most significant source of exergy destruction and exergy losses in the bio-system (plant–soil system) and their location of occurrence.
- Evaluate the effect of various natural phenomena (weathering, acid rain, etc.) on the bio-system exergy efficiency.
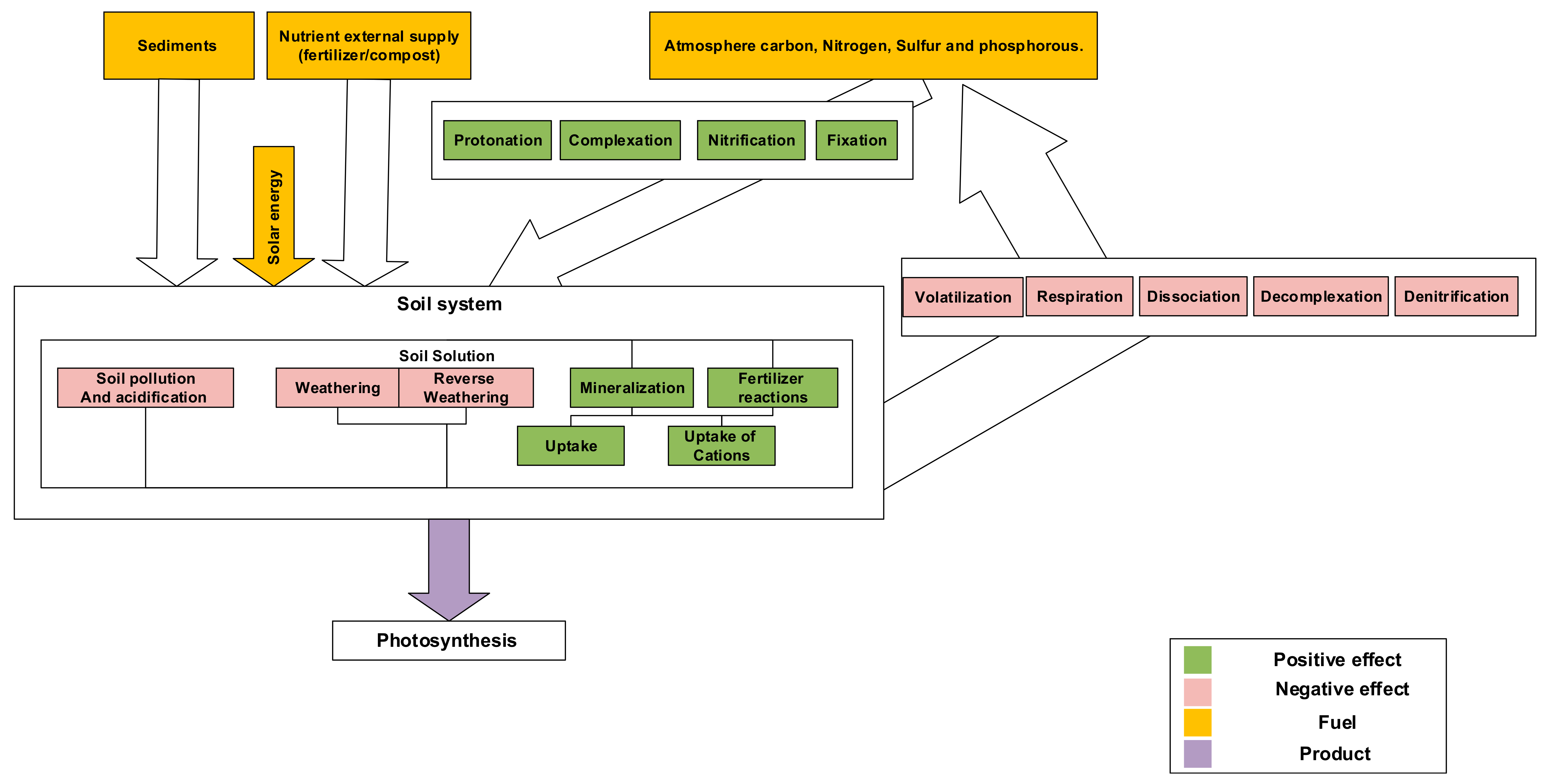
2. Materials and Methods
- Biochemical processes, including interactions between biota and the atmosphere (e.g., photosynthesis, respiration, N2 fixation), and interactions between biota and soil solution (e.g., assimilation and mineralization).
- Geochemical and soil chemical processes, including interactions between solution and the soil solid phase (e.g., cation exchange, adsorption, chemical weathering).
- Chemical reactions in solution (e.g., hydrolysis, complexation reactions) or between solution and atmosphere (e.g., degassing of CO2).
2.1. Exergy Analysis of Electron Transport Chain
2.2. The Exergy of Biochemical Reactions
3. Results
3.1. Exergy Loss and Destruction of Different Ecosystems Interactions
3.1.1. Weathering
3.1.2. Dissolution and Precipitation
3.1.3. Soil Acidification and Leaching
3.1.4. Total Exergy Losses of Natural Processes in the Soil System
3.1.5. Exergy Loss and Exergy Destruction of Human Activity in the Soil
3.1.6. Exergy Losses from Destructions in Processes of the Soil System
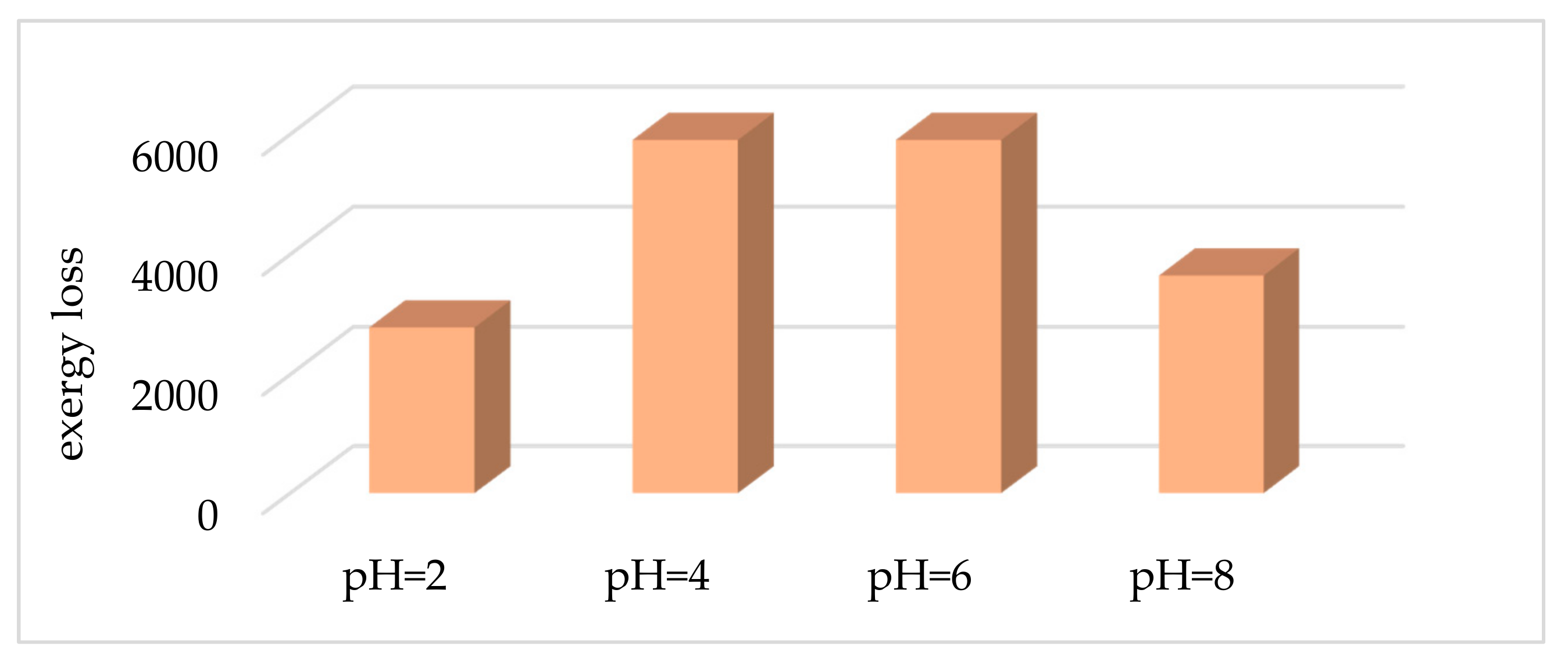
3.1.7. Exergy Losses from Leaching Based on pH
3.1.8. The Effects of Adding Fertilizers to the Soil
4. Discussion
4.1. Exergy Destructions Nutrient Supply for Plant Growth in the Soil System
4.2. Loss and Destruction of Exergy Due to Soil pH Levels in the Bio-System
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A. Soil Reactions and Exergy Analysis
| Reaction | ∆G (kJ/mole) | ||
|---|---|---|---|
| −51.87 | 1057.90 | 211.00 | |
| 57.72 | 1694.80 | 426.10 | |
| −728.05 | 1532.00 | 119.87 | |
| −649.12 | 2168.90 | 957.85 | |
| 514.29 | 1033.40 | 120.96 | |
| 593.22 | 1670.30 | 958.94 | |
| −846.98 | 1389.20 | 542.30 | |
| −737.38 | 2026.10 | 757.40 | |
| 1063.26 | 1461.30 | 218.04 | |
| 2063.07 | 1461.30 | 433.14 | |
| 2793.47 | 1500.70 | 121.31 | |
| 2872.40 | 2137.60 | 959.29 |
| Reaction | ∆G (kJ/mole) | (kJ/mole) | (kJ/mole) |
| −287 | 542.37 | 234.99 | |
| −871 | 839.14 | 1688.86 | |
| −587 | 614.47 | 703.73 | |
| −275 | 673.17 | 177.77 | |
| −237 | 240.07 | 476.17 | |
| −209 | 1478.57 | 112.77 | |
| −76 | 110.87 | 53.39 | |
| −31 | 1417.39 | 698.59 |
| Reaction | ∆G (kJ/mole) | (kJ/mole) | (kJ/mole) |
| −705.82 | 218.04 | 130.25 | |
| −2223.46 | 433.14 | 396.72 | |
| −1125.80 | 121.31 | 66.89 | |
| −1032.98 | 959.29 | 356.43 | |
| 406.84 | 151.10 | 43.66 | |
| −251.95 | 1004.47 | 916.72 | |
| −232.05 | 339.70 | 232.05 | |
| 1253.57 | 664.59 | 588.98 | |
| −159.72 | 107.80 | 267.52 | |
| 2504.86 | 1867.74 | 637.12 | |
| −746.27 | 1281.90 | 88.07 | |
| −876.91 | 542.37 | 334.54 | |
| −2512.99 | 2930.00 | 2512.99 | |
| 739.00 | 542.30 | 196.70 | |
| 494.53 | 1008.85 | 514.32 | |
| −96.97 | 1523.59 | 1426.62 | |
| 3691.34 | 1916.60 | 1774.74 | |
| 1164.40 | 1272.20 | 107.80 | |
| 69.60 | 1272.20 | 1202.60 | |
| 2249.43 | 1272.20 | 977.23 | |
| 3013.02 | 3154.20 | 141.18 | |
| −120.91 | 770.26 | 649.35 | |
| −3592.54 | 2435.35 | 1157.19 | |
| −2271.66 | 1440.66 | 831 | |
| Amorphous Hydroxides | ∆G (kJ/mole) | ||
|---|---|---|---|
| Al(OH)3 | −1141.76 | 1154.00 | 7617.78 |
| Fe(OH)3 | −695.86 | 40.47 | 210.98 |
| Mn(OH)2 | −663.14 | … | … |
| sum | 1194.47 | 7828.76 | |
| Silicates | |||
| ß-CaSiO 3 (wollastonite) + 2 H+ + H2O = Ca2++ H4SiO4 | −75.74 | 75.74 | 663.50 |
| CaSiO3 (pseudowollastonite) + 2 H+ + H2O = Ca2++ H4SiO4 | −81.22 | 81.22 | 663.50 |
| ß-Ca2SiO4 (larnite) + 4 H+↔2 Ca2+ + H4SiO4 | −226.14 | 226.14 | 1325.20 |
| ?- Ca2SiO4 (Ca olivine) + 4 H+↔2 Ca2+ + H4SiO4 | −215.86 | 215.86 | 1325.20 |
| Aluminosilicates | |||
| CaAl2SiO6 (pyroxene) + 8 H+↔Ca2+ + 2 Al3+ + H4SiO4+2 H2O | −201.20 | 201.20 | 2650.40 |
| CaAl2Si2O8 (Ca-glass) + H+↔Ca2+ + 2 Al3+ + 2 H4SiO4 | −193.55 | 193.55 | 2650.40 |
| CaAl2Si2O8 (hexagonal anorthite) + 8 H+↔Ca2+ + 2 Al3+ + 2 H4SiO4 | −148.97 | 148.97 | 2650.40 |
| CaAl2Si2O8 (anorthite) + 8 H+↔Ca2++ 2 Al3+ + 2 H4SiO4o | −133.16 | 133.16 | 2650.40 |
| CaAl2Si2O82 H2O (lawsonite) 8 H+↔Ca2+ + 2 Al3+ + 2 H4SiO4+ 2 H2O | −100.11 | 100.11 | 2650.40 |
| CaAl2Si2O4O12i2 H2O (wairakite) + 8 H+↔Ca2+ + 2 Al3+ + 2 H4SiO4 | −91.61 | 91.61 | 2650.40 |
| Ca2Al4Si8O24i7 H2O (leonhardite) + 16 H+ + H2O↔2 Ca2++4 Al3+ + 8 H4SiO4 | −98.69 | 98.69 | 5301.70 |
| CaMg(SiO3)2 (diopsite) + 4 H+ + 2 H2O↔Ca2++ Mg2+ + 2 H4SiO4 | −120.77 | 120.77 | 1327.00 |
| Photosynthesis | Efficiency | |||
|---|---|---|---|---|
| PAR Reflection | 9977 | 9977 | 0 | 100 |
| Non-PAR Reflection | 13,226 | 661 | 12,564 | 50 |
| Photosystem II absorption | 5319 | 4193 | 1126 | 78.8 |
| Photosystem I absorption | 5319 | 4074 | 1246 | 76.6 |
| Photosystem II ETC | 4209 | 2200 | 2009 | 52.3 |
| Photosystem I ETC | 4901 | 2401 | 2500 | 49 |
| ATP synthase | 1372 | 992 | 381 | 72.2 |
| Calvin cycle (dark reaction) | 3509 | 2848 | 661 | 81.2 |
| overall | 23,334 | 2848 | 20,487 | 12.2 |
| Reaction | Efficiency | ||
|---|---|---|---|
| 335.27 | 169.78 | 49.36 |
| Reaction | ΔG (kJ/mole) | ||
|---|---|---|---|
| 55.87 | 55.87 | 211.00 | |
| −72.80 | 72.80 | 119.87 | |
| −514.29 | 514.29 | 638.90 | |
| −57.70 | 57.70 | 426.10 | |
| 649.12 | 649.12 | 957.85 | |
| −593.22 | 593.22 | 962.59 | |
| Surface Volatilization | |||
| −1243.65 | 1243.65 | 2933.40 | |
| −3106.80 | 310.00 | 1358.70 | |
| Ion Exchange | ∆G (KJ/mole) | |
|---|---|---|
| 325.70 | 504.90 | |
| 179.60 | 175.80 | |
| 169.95 | 2413.00 | |
| 169.78 | 335.06 | |
| 59.77 | 1988.52 | |
| 51.08 | 662.60 | |
| 7.62 | 376.40 | |
| −23.26 | 339.20 | |
| −233.42 | 366.60 | |
| … | ||
| 125.39 | 376.40 | |
| 78.99 | 78.99 | |
| 71.35 | 1344.68 | |
| −109.40 | 888.20 | |
| … | … | |
| −212.44 | 336.60 | |
| −226.88 | 729.10 |
| Reaction | ||
|---|---|---|
| Slow Reactions in Carbon Cycle | ||
| 32.4 | 44.88 | |
| 81.24 | 2276.98 | |
| 48.84 | 60.18 | |
| Fast Reactions in Carbon Cycle | ||
| 510.17 | 20.38 | |
Methane formation | 105.4 | 548.14 |
Soil inorganic carbon | 201.16 | 2206.18 |
| Reaction | ||
|---|---|---|
| Nitrogen | ||
| 57.98 | 1793.5 | |
| 130.39 | 1461.3 | |
| 93.79 | 1461.3 | |
| 169.95 | 2260 | |
| Complexes | Log K | ΔG (kJ/mole) | ||
|---|---|---|---|---|
| CaF2 (fluorite)↔Ca2+ + 2F− | −10.41 | 59.42 | 70.82 | 130.23 |
| Ca2 + Cl−↔CaCl+ | −1.00 | 5.71 | 822.31 | 828.02 |
| Ca2++0/5O2 + 2 Cl−↔CaCl2 | 0.00 | 0.00 | 903.70 | 903.70 |
| Ca2++ CO2(g) + H2O↔CaHCO3+H+ | −6.70 | 38.24 | 788.04 | 826.28 |
| Ca2++ CO2(g) + H2O↔CaCO3 + 2 H+ | −15.01 | 85.67 | 835.47 | 921.14 |
| Ca2++ NO3−↔CaNO3+ | −4.80 | 27.40 | 763.21 | 790.61 |
| Ca2++ 2 NO3−↔Ca(NO3)2 | −4.50 | 25.68 | 767.81 | 793.50 |
| Ca2+ + 2 H2O↔Ca(OH)2 + 2 H+ | −27.99 | 159.76 | 891.06 | 1050.82 |
| Ca2++ H2PO4−↔Ca H2PO4 | 1.40 | −7.99 | 1058.65 | 1050.66 |
| Ca2+ + H2PO4−↔CaHPO4 + H+ | −4.46 | 25.46 | 1092.10 | 1117.56 |
| Ca2+ + H2PO4−↔CaPO4−+ 2 H+ | −13.09 | 74.71 | 1141.36 | 1216.07 |
| Ca2+ + SO42−↔CaSO4 | 2.31 | −13.18 | 1325.62 | 1312.43 |
| Crystal Modification Dissolution Reaction | Log K | ΔG (kJ/mole) | ||
|---|---|---|---|---|
| CaSO4 i2H2O↔Ca2+ + SO42− + 2H2O | 4.60 | 26.26 | 26.26 | 26.26 |
| CaCO3↔Ca2++ CO32− | 8.35 | 47.66 | 48.66 | 1 |
| Fe(OH)3↔Fe3+ + 3 OH− | 38.7 | 220.89 | 260.49 | 39.60 |
| Al(OH)3↔Al3+ + 3 OH− | 33.8 | 192.92 | 566.32 | 373.40 |
| Al(OH)3↔Al3+ + 3 OH− | 33.0 | 188.35 | 3922.75 | 3734.40 |
| Al(OH)2 H2PO4↔Al3+ + 2 OH− + H2PO4 | −30.5 | −174.08 | 174.08 | 174.08 |
| Fe(OH)2 H2PO4↔Fe3+ + 2 OH− + H2PO4 | −35.0 | −199.77 | 199.77 | 199.77 |
| −0.09 | 0.50 | 1677.97 | 0.50 | |
| 13 | 74.71 | 1752.18 | 74.71 | |
| 30.5 | −174.08 | 2778.65 | 174.08 | |
| Strengite | 35.0 | −199.77 | 2238.86 | 199.77 |
| Protonation | ΔG (kJ/mole) | ||
|---|---|---|---|
| −5.72 × 10−14 | 8.94 × 102 | 8.96 × 102 | |
| 1.02 × 103 | 1.02 × 103 | 1.54 × 103 | |
| 6.12 × 103 | 6.12 × 103 | 6.80 × 103 | |
| −1.32 × 102 | 1.32 × 102 | 1.64 × 102 | |
| −2.19 × 102 | 2.19 × 102 | 9.51 × 102 | |
| −8.20 × 10 | 8.20 × 10 | 4.62 × 102 | |
| −3.59 × 103 | 1.16 × 103 | 2.44 × 103 | |
| −7.46 × 102 | 8.81 × 101 | 1.28 × 103 | |
| Soil Acidification | |||
| 1.25 × 103 | 5.89 × 102 | 6.65 × 102 | |
| −2.27 × 102 | 2.27 × 102 | 7.29 × 102 | |
| −1.32 × 10 | 1.33 × 103 | 1.31 × 103 | |
| Al(OH)3↔Al3+ + 3 OH− | 1.93 × 102 | 5.66 × 102 | 3.73 × 102 |
| Reactions | ΔG (kJ/mole) | ||
|---|---|---|---|
| Soil acidity adjustment | −287.86 | 287.86 | 503.36 |
| 443.00 | 240.12 | 678.90 | |
| Acid Rain | |||
| Limestone Neutralization | |||
| CaCO3 + H2SO4 → CaSO4 + H2CO3 | −179.70 | 149.90 | 179.70 |
| H2CO3 → CO2 gas + H2O | −1019.67 | 521.82 | 1019.67 |
| Al(OH)3 + H2SO4 → Al2(SO4)3 + H2CO3 | −1141.76 | 1154.00 | 7617.78 |
| Cation Exchange Reactions | |||
| −233.42 | 133.18 | 233.42 | |
| −226.88 | 502.22 | 226.88 | |
| Mineral Dissolution | |||
|---|---|---|---|
| Reaction | Log (K) | ΔG (kJ/mole) | |
| CaSO4 (gypsum)↔Ca2+ + SO42− | −4.60 | 11.40 | 11.40 |
| CaCO3 (calcite)↔Ca2+ + CO32− | −8.35 | 20.70 | 20.70 |
| Fe(OH)3 (amorphous)↔Fe3+ + 3OH− | −38.70 | 95.93 | 95.93 |
| Al(OH)3 (Gibbsite)↔Al3+ + 3OH− | −33.00 | 81.80 | 81.80 |
| Fe(OH)2H2PO4 (Strengite)↔Fe3+ + 2OH− + H2PO4 | −35.00 | 86.76 | 86.76 |
| Reaction | Log K | ΔG (kJ/mole) | |
|---|---|---|---|
| … | −3592.54 | 1157.19 | |
| … | −746.27 | 88.07 | |
| CaS04 i2H2O↔Ca2+ + SO42- + 2H2O | 4.6 | 26.26 | 26.26 |
| CaCO3↔Ca2+ + CO32− | 8.35 | 47.66 | 48.66 |
| Fe(OH)3↔Fe3+ + 3 OH− | 38.7 | 220.89 | 260.49 |
| Al(OH)3↔Al3+ + 3 OH− | 33.8 | 192.92 | 566.32 |
| Al(OH)3↔Al3+ + 3 OH− | 33 | 188.35 | 3922.75 |
| Al(OH)2H2PO4↔Al3+ + 2 OH− + H2PO4 | −30.5 | −174.08 | 174.08 |
| Fe(OH)2H2PO4↔Fe3+ + 2 OH− + H2PO4 | −35 | −199.77 | 199.77 |
| −0.09 | 0.50 | 1677.97 | |
| −13.09 | 74.71 | 1752.18 | |
| Variscite | 30.5 | −174.08 | 2778.65 |
| Strengite | 35 | −199.77 | 2238.86 |
| Reaction Type | Reaction Formula | |
|---|---|---|
| carbonation | CaCO3 + H2CO3→Ca (HCO3)2 | 527.54 |
| Solution | Mineral (Fe, Al, and Mn)+H2O→Anions+ Cations | 264.49 |
| Hydrolysis | 3KAl4 + Si3Og + 14H2O→K (AlSi3)4Al24O10(OH)2 + 6Si(OH)4 + 2KOH | 6119.50 |
| Hydration | Mineral (Mg, Ca, Mn, Fe, and Al)+ H2O→Water enters the mineral Structure of anhydrous mineral | 189.13 |
| Oxidation | Fe2+ + 2H2O + ½ O2↔Fe (OH)3 + H+ | 171.59 |
| And similar for Mn2+ | … | |
| Reduction | 2Fe2O3 (Hematite) − O2→4FeO (Ferrous Oxide) – Reduced form | 287.86 |
| Complexation | Complexation reaction of Al, Mn, and Fe. | 480.87 |
| Reaction | ΔG (kJ/mole) | ||
|---|---|---|---|
| Rainfall | |||
| 856.42 | 856.42 | 2582.8 | |
| Reaction | Log K | |
|---|---|---|
| Oxides, Carbonates, and Sulfates | ||
| PbO(yellow)+2H+↔Pb2+ +H2O | 12.89 | 31.95 |
| PbO(red)+2H+↔Pb2+ +H2O | 12.72 | 31.53 |
| Pb(OH)2+2H+↔Pb2+ +2H2O | 8.16 | 20.23 |
| Pb3O4+8H+↔3 Pb2+ +4H2O | 73.79 | 182.91 |
| Pb2CO3Cl2+2H+ | 49.68 | 123.15 |
| Pb3(CO3)2(OH)2+6H+ | 4.65 | 11.53 |
| PbCO3.PbO+4H+ | −1.80 | 4.46 |
| PbSO4 | 17.51 | 43.40 |
| PbSO4.PbO | 17.39 | 43.11 |
| PbSO4↔Pb2+ + SO4 | −7.79 | 19.31 |
| PbSO4.PbO + 2H+ | −0.19 | 0.47 |
| PbSO4.2PbO + 4H+ | 11.01 | 27.29 |
| PbSO4.3PbO + 6H+ | 22.30 | 55.28 |
| Silicates | ||
| PbSiO3+2H+ + H2O | 5.94 | 14.72 |
| Pb2SiO4 + 4H+ | 18.45 | 45.73 |
| phosphates | 0.00 | |
| Pb(H2PO4)2↔Pb2+ + 2H2PO4− | −9.85 | 24.42 |
| PbHPO4 + H+ | −4.25 | 10.53 |
| Pb3(PO4)2 + 4H+ | −5.26 | 13.04 |
| Pb4O(PO4)2 + 6H+ | −2.24 | 5.55 |
| Pb5(PO4)3OH + 7H+ | −4.14 | 10.26 |
| Pb5(PO4)3Br + 6H+ | −19.49 | 48.31 |
| Pb5(PO4)3Cl + 6H+ | −25.05 | 62.09 |
| Pb5(PO4)3F + 6H+ | −12.98 | 32.18 |
| Other Minerals | ||
| soil_Pb↔Pb2+ | −8.50 | 21.07 |
| PbMoO4↔Pb2+ + MoO4 | −16.04 | 39.76 |
| PbS↔Pb2+ + S2− | −27.51 | 68.19 |
| Pb2+ + 2e↔Pb | −4.33 | 10.73 |
| Hydrolysis Species | ||
| Pb2+ + H2O | −7.70 | 19.09 |
| Pb2+ + 2H2O | −17.50 | 43.38 |
| Pb2+ + 3H2O | −28.09 | 69.63 |
| Pb2+ + 4H2O | −39.49 | 97.89 |
| 2Pb2+ + H2O | −6.40 | 15.86 |
| 3Pb2+ + 4H2O | −23.89 | 59.22 |
| 4Pb2+ + 4H2O | −20.89 | 51.78 |
| 6Pb2+ + 8H2O | −43.58 | 108.03 |
| Pb2+ + 4Br− | 2.30 | 5.70 |
| Pb2+ + Cl− | 1.60 | 3.97 |
| Pb2+ + 2Cl− | 1.78 | 4.41 |
| Pb2+ + 3Cl− | 1.68 | 4.16 |
| Pb2+ + 4Cl− | 1.38 | 3.42 |
| Pb2+ + F− | 1.49 | 3.69 |
| Pb2+ + 2F− | 2.27 | 5.63 |
| Pb2+ + 3F− | 3.42 | 8.48 |
| Pb2+ + 4F− | 3.10 | 7.68 |
| Pb2+ + I− | 1.92 | 4.76 |
| Pb2+ + 2I− | 3.15 | 7.81 |
| Pb2+ + 3I− | 3.92 | 9.72 |
| Pb2+ + 4I− | 4.50 | 11.15 |
| Pb2+ + NO3− | 1.17 | 2.90 |
| Pb2+ + 2NO3− | 1.40 | 3.47 |
| Pb2+ + H2PO4−↔PbH2PO4+ | 1.50 | 3.72 |
| Pb2+ + H2PO4−↔PbHPO4+H+ | −4.10 | 10.16 |
| Pb2+ + P2O7 | 11.30 | 28.01 |
| Pb2+ + SO4 | 2.62 | 6.49 |
| Pb2+ + 2SO4 | 3.47 | 8.60 |
| Reaction | Log K | |
|---|---|---|
| Zn2+ + H2O | −7.69 | 19.06 |
| Zn2+ + 2H2O | −16.80 | 41.64 |
| Zn2+ + 3H2O | −27.68 | 68.61 |
| Zn2+ + 4H2O | −38.29 | 94.91 |
| Zn2+ + Cl− | 0.43 | 1.07 |
| Zn2+ + 2Cl− | 0.00 | 0.00 |
| Zn2+ + 3Cl− | 0.50 | 1.24 |
| Zn2+ + 4Cl− | 0.20 | 0.50 |
| Zn2+ + H2PO4− | 1.60 | 3.97 |
| Zn2+ + H2PO4− | −3.90 | 9.67 |
| Zn2+ +NO3− | 0.40 | 0.99 |
| Zn2+ + 2NO3− | −0.30 | 0.74 |
| Zn2+ + SO4 | 2.33 | 5.78 |
| Zn(OH)2 + 2H+ | −25.80 | 63.95 |
| a-Zn(OH)2 + 2H+ | 12.48 | 30.94 |
| B-Zn(OH)2 + 2H+ | 12.19 | 30.22 |
| gamma-Zn(OH)2 + 2H+ | 11.78 | 29.20 |
| E-Zn(OH)2 + 2H+ | 11.74 | 29.10 |
| ZnO + 2H+ | 11.53 | 28.58 |
| ZnCO3 + 2H+ | 11.16 | 27.66 |
| soil_Zn + 2H+ | 7.91 | 19.61 |
| ZnFe2O4 + 8H+ | 5.80 | 14.38 |
| ZnSiO3+2H+ + H2O | 9.85 | 24.42 |
| Zn2SiO4 + 4H+ | 13.15 | 32.60 |
| ZnCl2↔Zn2+ + 2Cl− | 7.07 | 17.53 |
| ZnSO4↔Zn2+ + SO4 | 3.41 | 8.45 |
| ZnO-2ZnSO4 + 2H+ | 19.12 | 47.40 |
| Zn(OH)2.ZnSO4 + 2H+ | 7.50 | 18.59 |
| Zn3(PO4)2.4H2O + 4H+ | 3.80 | 9.42 |
| Reaction | Log K | |
|---|---|---|
| Cd2+ + 2e↔Cd | −13.64 | 33.81 |
| CdO + 2H+ | 15.14 | 37.53 |
| B?_Cd(OH)2 + 2H+ | 13.65 | 33.84 |
| CdCO3 + 2H+ | 6.16 | 15.27 |
| CdSiO3+2H+ + H2O | 7.63 | 18.91 |
| CdSO4↔Cd + SO4 | −0.04 | 0.10 |
| CdSO4.H2O↔Cd + SO4 + H2O | −1.59 | 3.94 |
| CdSO4.2Cd(OH)2 + 4H+ | 22.65 | 56.15 |
| 2CdSO4.Cd(OH)2 + 2H+ | 6.73 | 16.68 |
| Cd3(PO4)2 + 4H+ | 1.00 | 2.48 |
| CdS↔Cd2+ + S2− | −27.07 | 67.10 |
| soil_Cd↔Cd2+ | −7.00 | 17.35 |
| Cd2+ + H2O | −10.10 | 25.04 |
| Cd2+ + 2H2O | −20.30 | 50.32 |
| Cd2+ + 3H2O | −33.01 | 81.83 |
| Cd2+ + 4H2O | −47.29 | 117.22 |
| Cd2+ + 5H2O | −61.93 | 153.51 |
| Cd2+ +6H2O | −76.81 | 190.40 |
| 2Cd2+ + H2O | −6.40 | 15.86 |
| 4Cd2+ + 4H2O | −27.92 | 69.21 |
| Cd2+ + Br− | 2.15 | 5.33 |
| Cd2+ + 2Br− | 3.00 | 7.44 |
| Cd2+ + 3Br− | 3.00 | 7.44 |
| Cd2+ + 4Br− | 2.90 | 7.19 |
| Cd2+ + Cl− | 1.98 | 4.91 |
| Cd2+ + 2Cl− | 2.60 | 6.44 |
| Cd2+ + 3Cl− | 2.40 | 5.95 |
| Cd2+ + 4Cl− | 2.50 | 6.20 |
| Cd2+ + I− | 2.28 | 5.65 |
| Cd2+ + 2I− | 3.92 | 9.72 |
| Cd2+ + 3I− | 5.00 | 12.39 |
| Cd2+ + 4I− | 6.00 | 14.87 |
| Cd2+ + NH4 | −0.73 | 1.81 |
| Cd2+ + 2NH4 | −14.00 | 34.70 |
| Cd2+ + 3NH4 | −21.95 | 54.41 |
| Cd2+ + 4NH4 | −30.39 | 75.33 |
| Cd2+ + CO2 + H2O | −5.73 | 14.20 |
| Cd2+ + CO2 + H2O | −14.06 | 34.85 |
| Cd2+ + NO3− | 0.31 | 0.77 |
| Cd2+ + 2NO3− | 0.00 | 0.00 |
| Cd2+ + H2PO4− | −4.00 | 9.92 |
| Cd2+ + P2O7 | 8.70 | 21.57 |
| Cd2+ + SO4 | 2.45 | 6.07 |
| Reaction | Log K | |
|---|---|---|
| CuO + 2H+ | 7.66 | 18.99 |
| Cu(OH)2 + 2H+ | 8.68 | 21.52 |
| CuCO3 + 2H+ | 8.52 | 21.12 |
| Cu2(OH)2CO3 + 4H+ | 12.99 | 32.20 |
| Cu3(OH)2(CO3)2 + 4H+ | 19.57 | 48.51 |
| a_CuFe2O4 + 8H+ | 10.13 | 25.11 |
| soil_Cu + 2H+ | 2.80 | 6.94 |
| CuSo4↔Cu2+ + SO4 | 3.72 | 9.22 |
| CuSo4/5H2O↔Cu2+ + SO5+H2O | −2.61 | 6.47 |
| CuO.CuSO4 + 2H+ | 11.50 | 28.51 |
| Cu4(OH)6SO4 + 6H+ | 15.35 | 38.05 |
| Cu4(OH)6SO4.1.3H2O + 6H+ | 17.27 | 42.81 |
| Cu3(PO4)2 + 4H+ | 2.24 | 5.55 |
| Cu3(PO4)2.2H2O + 4H+ | 0.34 | 0.84 |
| Cu2P2O7↔2Cu2+ + P2O7 | −15.22 | 37.73 |
| Cu2+ + H2O | −7.70 | 19.09 |
| Cu2+ + 2H2O | −13.78 | 34.16 |
| Cu2+ + 3H2O | −26.75 | 66.31 |
| Cu2+ + 4H2O | −39.59 | 98.14 |
| 2Cu2+ + 2H2O | −10.68 | 26.47 |
| Cu2+ + Cl− | 0.40 | 0.99 |
| Cu2+ + 2Cl− | −0.12 | 0.30 |
| Cu2+ + 3Cl− | −1.57 | 3.89 |
| Cu2+ + CO2 + H2O | −5.73 | 14.20 |
| Cu2+ + CO2 + H2O | −11.43 | 28.33 |
| Cu2++2CO2 + 2H2O | −26.48 | 65.64 |
| Cu2+ + NO3− | 0.50 | 1.24 |
| Cu2+ + 2NO3− | −0.40 | 0.99 |
| Cu2+ + H2PO4− | 1.59 | 3.94 |
| Cu2+ + H2PO4− | −4.00 | 9.92 |
| Cu2+ + 2H+ + P2O7 | 18.67 | 46.28 |
| Cu2+ + P2O7 | 14.78 | 36.64 |
| 2Cu2+ + SO4 | 6.64 | 16.46 |
| Cu2+ mineral | −0.03 | 0.07 |
| Cu2+ mineral | 2.36 | 5.85 |
| Cu2+ + e− | 2.62 | 6.49 |
| Cu+ + e | 8.87 | 21.99 |
| Cu2+ + 2e | 11.49 | 28.48 |
| CuO2 + 2H+ | −2.17 | 5.38 |
| CuOH + H+ | −0.70 | 1.74 |
| a?_Cu2Fe2O4 + 8H+ | −13.53 | 33.54 |
| Cu2SO4↔2Cu+ + SO4 | −1.95 | 4.83 |
| Cu+ + Cl−↔CuCl | 2.70 | 6.69 |
| Cu+ + 2Cl−↔CuCl2− | 5.51 | 13.66 |
| Cu2 + 3Cl-↔CuCl3 | 5.70 | 14.13 |
| 2Cu+ + 4Cl−↔Cu2Cl4 | 13.10 | 32.47 |
| Reaction | ΔG (kJ/mole) | ||
|---|---|---|---|
| Nitrogen | |||
| (1) Urea | |||
| −7771.1 | 7537.41 | 15,308.51 | |
| 738.5 | 738.5 | 1605.16 | |
| −2717.2 | 2717.2 | 2796.36 | |
| −309.26 | 103.88 | 103.3 | |
| −818.4 | 836.4 | 948.4 | |
| (2) Ammonium Sulfate | |||
| −1287.73 | 652.43 | 660.6 | |
| 1852.9 | 1264.1 | 1338.4 | |
| −1454.4 | 1457.62 | 1557.7 | |
| 1974.2 | 854.6 | 2061.2 | |
| (3) Calcium Ammonium Nitrate | |||
| −816 | 1182 | 2052 | |
| 2325.2 | 2325.2 | 2336.54 | |
| −2717.2 | 335.06 | 422.06 | |
| −309.26 | 226.64 | 412.56 | |
| −3535.6 | 4303.2 | 749.6 | |
| Phosphorous | |||
| Acidification | |||
| −2122.6 | 764.8 | 1298.5 | |
| at pH<7/7 | 65.7 | 396.7104 | 1297.6 |
| −2875.5 | 2825.5 | 5724 | |
| −3214.42 | 1509.98 | 1764.6 | |
| Phosphate Fertilizer | |||
| −15,460.45 | 13,862.95 | 29,323.4 | |
| Phosphate Fertilizer—Single Super Phosphate | |||
| 2225.4 | 1575.3 | 3325.2 | |
| −3322.6 | 6777.28 | 8867.08 | |
| 33,865 | 29,859.64 | 63,724.64 | |
| 2 | 14,874 | 62,783.6 | 84,403.4 |
References
- Jørgensen, S.E.; Mejer, H. A holistic approach to ecological modeling. Ecol. Modell. 1979, 7, 169–189. [Google Scholar] [CrossRef]
- Wall, G. Introduction To Life Support Systems and Sustainable. UNESCO—Encyclopedia Life Support Systems (UNESCO-EOLSS). 2002. Available online: http://www.eolss.net (accessed on 20 November 2020).
- Chen, G.Q. Scarcity of exergy and ecological evaluation based on embodied exergy. Commun. Nonlinear Sci. Numer. Simul. 2006, 11, 531–552. [Google Scholar] [CrossRef]
- Jorgensen, S.E. Toward a consistent pattern of ecosystem theories. Sci. World J. 2001, 1, 71–75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kay, J.J.; Schneider, E.D. Thermodynamics and Measures of Ecological Integrity. In Ecological Indicators; Springer: Boston, MA, USA, 1992; Volume 1, pp. 159–182. [Google Scholar] [CrossRef]
- Kay, J.J. Handbook of Ecosystem Theories and Management; Jørgensen, S.E., Müller, F., Eds.; CRC Press—Lewis Publishers: Boca Raton, FL, USA, 2000; pp. 135–160. [Google Scholar]
- Patten, B.C.; Kraba, M.S.; Jorgensen, S.E. Ecosystems emerging: 1. Conservation. Ecol. Model. 1997, 96, 221–284. [Google Scholar] [CrossRef]
- Patten, B.C. Ecosystems emerging: 2. Dissipation. Ecol. Model. 1999, 117, 3–39. [Google Scholar]
- Jørgensen, S.E.; Patten, B.C.; Straškraba, M. Ecosystems emerging: Openness. Ecol. Model. 1999, 117, 41–64. [Google Scholar] [CrossRef]
- Jørgensen, S.E.; Patten, B.C.; Stras, M. Ecosystems emerging: 4. Growth. Ecol. Model. 2000, 126, 249–284. [Google Scholar] [CrossRef]
- Patten, B.C.; Straškraba, M.; Jørgensen, S.E. Ecosystems emerging. 5: Constraints. Ecol. Model. 2011, 222, 2945–2972. [Google Scholar] [CrossRef]
- Straškraba, M.; Jørgensen, S.E.; Patten, B.C. Ecosystems emerging: 6. Differentiation. Ecol. Model. 2014, 278, 29–51. [Google Scholar] [CrossRef]
- Jørgensen, S.E. A New Ecology: Systems Perspective; Elsevier: Amsterdam, The Netherlands, 2007; Volume 1. [Google Scholar]
- Petela, R. An approach to the exergy analysis of photosynthesis. Sol. Energy 2008, 82, 311–328. [Google Scholar] [CrossRef]
- Silva, C.S.; Seider, W.D.; Lior, N. Exergy efficiency of plant photosynthesis. Chem. Eng. Sci. 2015, 130, 151–171. [Google Scholar] [CrossRef] [Green Version]
- Lems, S.; van der Kooi, H.J.; Arons, J.D.S. Thermodynamic analysis of the living cell: Design of an exergy-based method. Int. J. Exergy 2007, 4, 339. [Google Scholar] [CrossRef]
- Borgert, J.A.; Moura, L.M. Exergetic analysis of glucose metabolism. Int. J. Exergy 2013, 12, 31–53. [Google Scholar] [CrossRef]
- Albarrán-Zavala, E.; Angulo-Brown, F. A Simple Thermodynamic Analysis of Photosynthesis. Entropy 2007, 9, 152–168. [Google Scholar] [CrossRef]
- Silow, E.A.; Mokry, A.V.; Jørgensen, S.E. Eco-Exergy Use for Ecosystem Health Assessment. Int. J. Exergy 2011, 1–22. Available online: https://www.researchgate.net/profile/Eugene_Silow2/publication/301747462_Eco-Exergy_use_for_ecosystem_health_assessment/links/5724d7b708ae586b21dbc4fe.pdf (accessed on 20 November 2020).
- Fath, B.D.; Jørgensen, S.E.; Patten, B.C.; Straškraba, M. Ecosystem growth and development. BioSystems 2004, 77, 213–228. [Google Scholar] [CrossRef]
- Dewulf, J.; Bösch, M.E.; de Meester, B.; van der Vorst, G.; van Langenhove, H.; Hellweg, S.; Huijbregts, M.A.J. Cumulative Exergy Extraction from the naural environment (CEENE): A comprehensive Life Cycle Impact Assessment method for resource accounting. Environ. Sci. Technol. 2007, 41, 8477–8483. [Google Scholar] [CrossRef]
- Rocco, M.V.; Cassetti, G.; Gardumi, F.; Colombo, E. Exergy Life Cycle Assessment of soil erosion remediation technologies: An Italian case study. J. Clean. Prod. 2016, 112, 3007–3017. [Google Scholar] [CrossRef]
- Mulder, J.A.N.; Cresser, M.S. Soil and Soil Solution Chemistry. Biogeochem. Small Catchments Tool Environ. Res. 1994, 107–132. [Google Scholar] [CrossRef]
- Warr, B.; Ayres, R. Accounting for soils: Towards an integrated sustainability and productivity assessment for soils. Insead Cmer 2004, 1–11. Available online: https://flora.insead.edu/fichiersti_wp/inseadwp2004/2004-19.pdf (accessed on 20 November 2020).
- David, M.M.C.; Nelson, L. Lehninger Principles of Biochemistry; Macmillan: New York, NY, USA, 2004. [Google Scholar]
- Lozano, M.A.; Valero, A. Theory of the exergetic cost. Energy 1993, 18, 939–960. [Google Scholar] [CrossRef]
- Bejan, A.; Tsatsaronis, G.; Moran, M.J. Thermal Design, and Optimization; John Wiley & Sons: Hoboken, NJ, USA, 1995. [Google Scholar]
- Petrakopoulou, F.; Tsatsaronis, G.; Morosuk, T.; Paitazoglou, C. Environmental evaluation of a power plant using conventional and advanced exergy-based methods. Energy 2012, 45, 23–30. [Google Scholar] [CrossRef]
- Tsatsaronis, G.; Pisa, J. Exergoeconomic evaluation and optimization of energy systems—Application to the CGAM problem. Energy 1994, 19, 287–321. [Google Scholar] [CrossRef]
- Shieh, J.H.; Fan, L.T. Estimation of energy (enthalpy) and exergy (availability) contents in structurally complicated materials. Energy Sources 1982, 6, 1–46. [Google Scholar] [CrossRef]
- Giovanol, R.; Schnoor, J.L.; Sigg, L.; Stumm, W.; Zobrist, J. Chemical weathering of crystalline rocks in the catchment area of acidic Ticino lakes, Switzerland. Clays Clay Miner. 1988, 36, 521–529. [Google Scholar] [CrossRef]
- Flowers, P.P.; Theopold, K.; Langley, R.; Robinson, W.R. Chemistry 2e. OpenStax. 2019. Available online: https://opentextbc.ca/chemistry2eopenstax/ (accessed on 20 November 2020).
- Du, Y.-J.; Wei, M.-L.; Reddy, K.R.; Liu, Z.-P.; Jin, F. Effect of acid rain pH on leaching behavior of cement stabilized lead-contaminated soil. J. Hazard. Mater. 2014, 271, 131–140. Available online: http://www.jstor.org/stable/2641247 (accessed on 15 March 2016). [CrossRef]
- Carpenter, S.R.; Caraco, N.F.; Correll, D.L.; Howarth, R.W.; Sharpley, A.N.; Smith, V.H. Nonpoint Pollution of Surface Waters with Phosphorus and Nitrogen. Ecol. Appl. 2016, 8, 559–568. [Google Scholar] [CrossRef]
- Ayangbenro, A.S.; Babalola, O.O. A New Strategy for Heavy Metal Polluted Environments: A Review of Microbial Biosorbents. Int. J. Environ. Res. Public Health 2017, 14, 94. [Google Scholar] [CrossRef]
- Willard, L.; Dsay, L. Chemical Equilibria in Soils; John Wiley & Sons: Hoboken, NJ, USA, 1979. [Google Scholar]
- Ehmann, J.L.; Chroth, G.S. Chapter 7: Nutrient Leaching; Trees, Crops and Soil Fertility, CABI Publishing: Wallingford, UK, 2003; pp. 151–166. [Google Scholar]
- Higashida, S.; Takao, K. Relations between soil microbial activity and soil properties in grassland. Soil Sci. Plant Nutr. 1986, 32, 587–597. [Google Scholar] [CrossRef] [Green Version]

| Reaction | |||
|---|---|---|---|
| Oxidative weathering of mineral | |||
| −287.856 | 287.856 | 503.36 | |
| Reverse weathering | |||
| 151.92 | 171.59 | 376.59 | |
| −960.22 | 73.19 | 393.47 | |
| Rainfall | |||
| 856.42 | 856.42 | 2582.8 | |
| Soil acidity adjustment | |||
| 443 | 240.12 | 678.9 |
| Reaction | log(K) | |
|---|---|---|
| −4.6 | 11.40 | |
| −8.35 | 20.6 | |
| −38.7 | 95.93 | |
| −33 | 81.80 | |
| −35 | 86.75 |
| Reaction | Log K | |
|---|---|---|
| … | 1157.18 | |
| … | 88.06 | |
| CaSO4↔Ca2+ + SO42− | 4.6 | 26.25 |
| CaCO3↔Ca2+ + CO32− | 8.35 | 48.65 |
| Fe(OH)3↔Fe3+ + 3 OH− | 38.7 | 260.48 |
| Al(OH)3↔Al3+ + 3 OH− | 33.8 | 566.31 |
| Al(OH)2H2PO4↔Al3+ + 2 OH− + H2PO4 | −30.5 | 174.08 |
| Fe(OH)2H2PO4↔Fe3+ + 2 OH− + H2PO4 | −35 | 199.76 |
| −0.08 | 1677.96 | |
| −13.09 | 1752.18 | |
| 30.5 | 2778.64 | |
| 35 | 2238.86 |
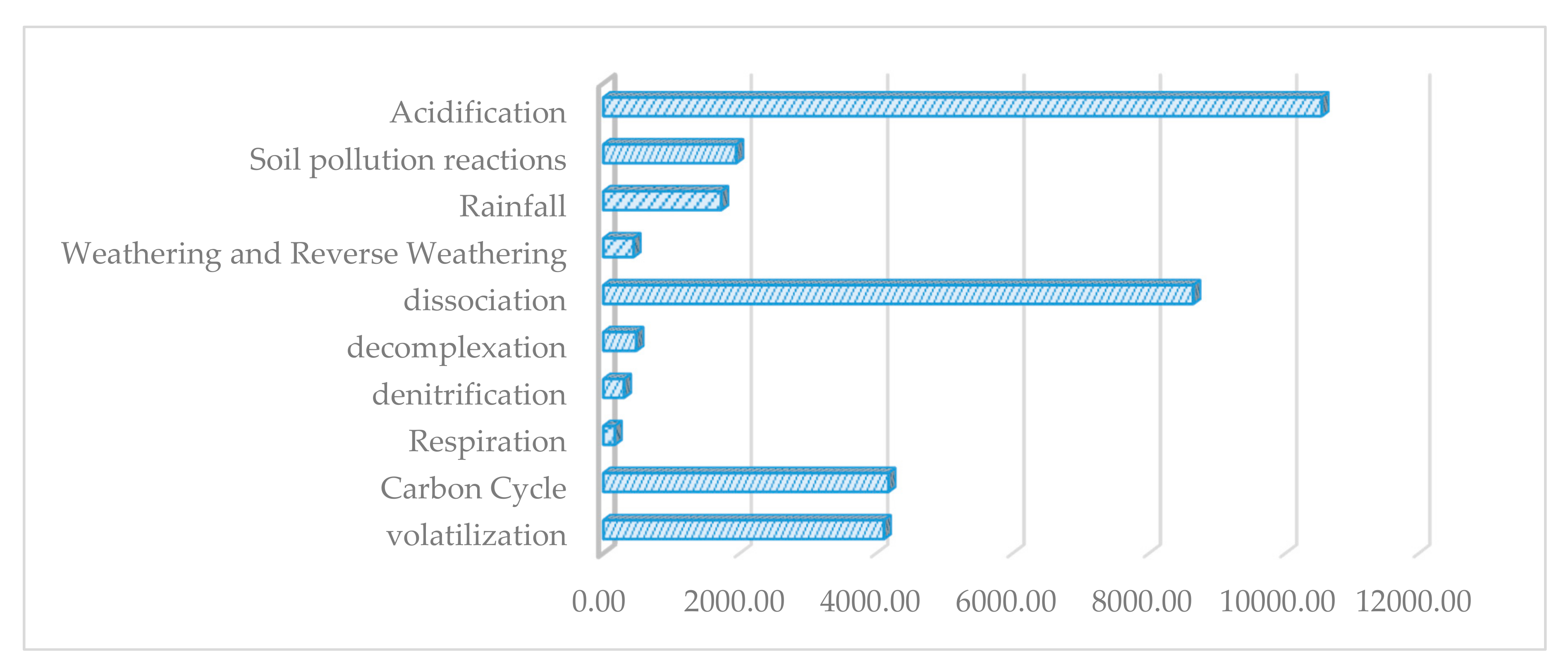
| Reaction | |
|---|---|
| Volatilization | 4111.76 |
| Carbon Cycle | 4177.53 |
| Respiration | 165.49 |
| Denitrification | 300.34 |
| De-complexation | 480.87 |
| Dissociation | 8648.41 |
| Weathering and Reverse Weathering | 440.17 |
| Rainfall | 1726.38 |
| Soil pollution reactions | 1946.24 |
| Acidification | 10,538.69 |
| Total | 32,535.89 |
| Element | Total Exergy Destruction (kJ/mole) | Exergy Destruction Increased Percent | |
|---|---|---|---|
| Pb | 1628.3 | 88,651.2 | 1.87 |
| Zn | 680.2 | 87,703.1 | 0.78 |
| Cd | 1353.7 | 88,376.6 | 1.55 |
| Cu | 991.8 | 88,014.8 | 1.14 |
| pH | |
|---|---|
| 2 | 2783.52 |
| 4 | 5904.97 |
| 6 | 5904.97 |
| 8 | 3649.42 |
| Fertilizer | Efficiency (%) | ||||
|---|---|---|---|---|---|
| Urea | 20,761.7 | 8716.3 | 11,933.4 | 112.0 | 42.0 |
| Ammonium Sulphate | 5617.9 | 1389.2 | 4228.8 | 0.0 | 24.7 |
| Calcium Ammonium Nitrate | 5972.8 | 1903.9 | 4068.9 | 0.0 | 31.9 |
| Phosphatic fertilizer | 29,323.40 | 15,001.68 | 13,862.95 | 458.77 | 51.2 |
| Phosphatic fertilizer-single Super Phosphate | 160,320.3 | 54,736.8 | 100,995.8 | 4587.7 | 34.1 |
| Total (kJ/mole) | ||||
|---|---|---|---|---|
| 29,252.81 | 51,840.28 | 23,299.9 | 9236 | 113,629 |
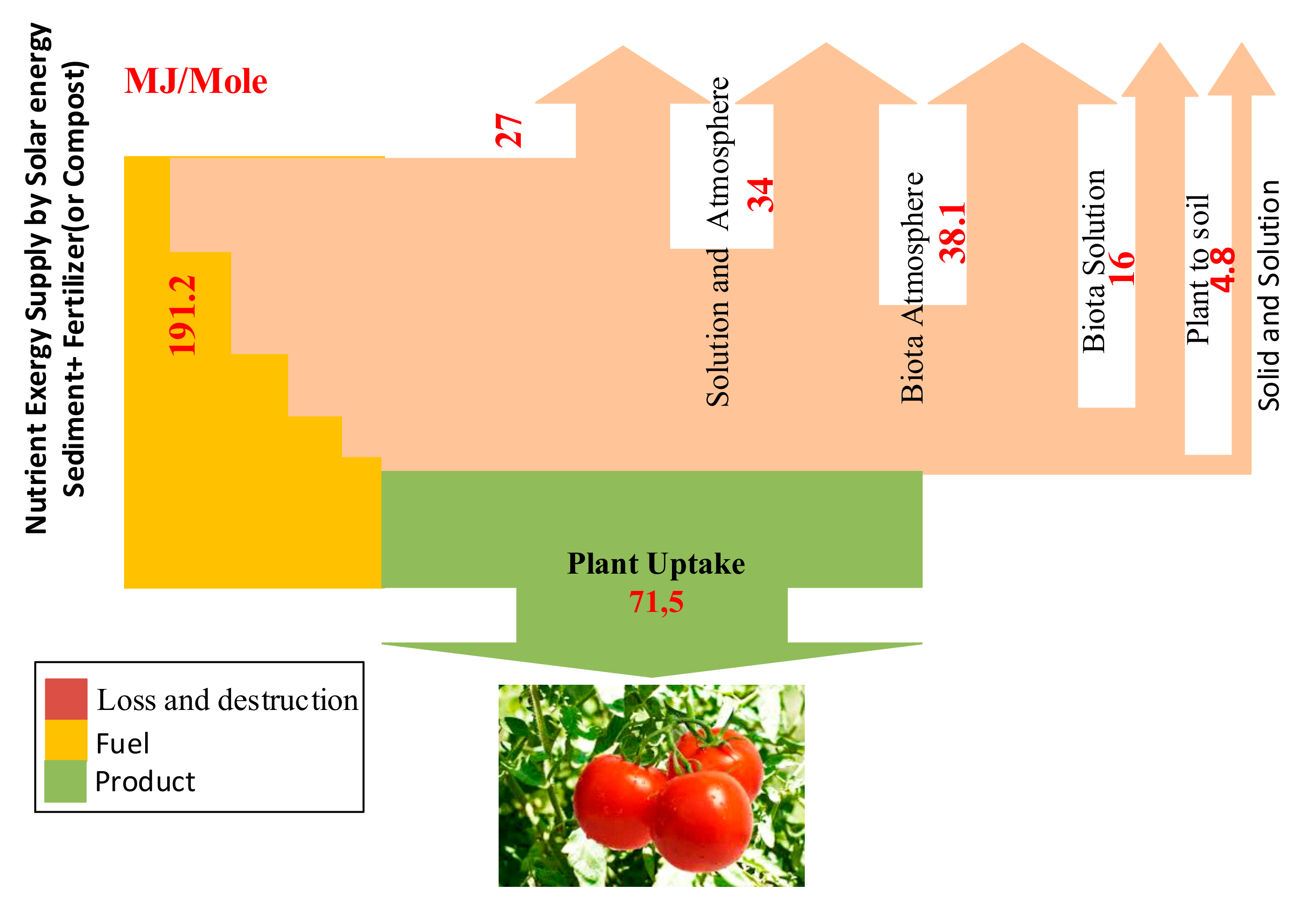
| Processes | Efficiency (%) | ||||
|---|---|---|---|---|---|
| Plant to Soil | 19,133.50 | 4099.82 | 13,307.31 | 1726.38 | 21.43 |
| Biota Solution | 67,758.59 | 29,781.03 | 25,492.62 | 12,484.94 | 43.95 |
| Biota Atmosphere | 51,194.08 | 17,173.84 | 25,565.45 | 8454.78 | 33.55 |
| Solution and Atmosphere | 45,925.62 | 18,296.86 | 18,199.14 | 9429.62 | 39.84 |
| Solid and Solution | 5038.48 | 270.28 | 4328.03 | 440.17 | 5.36 |
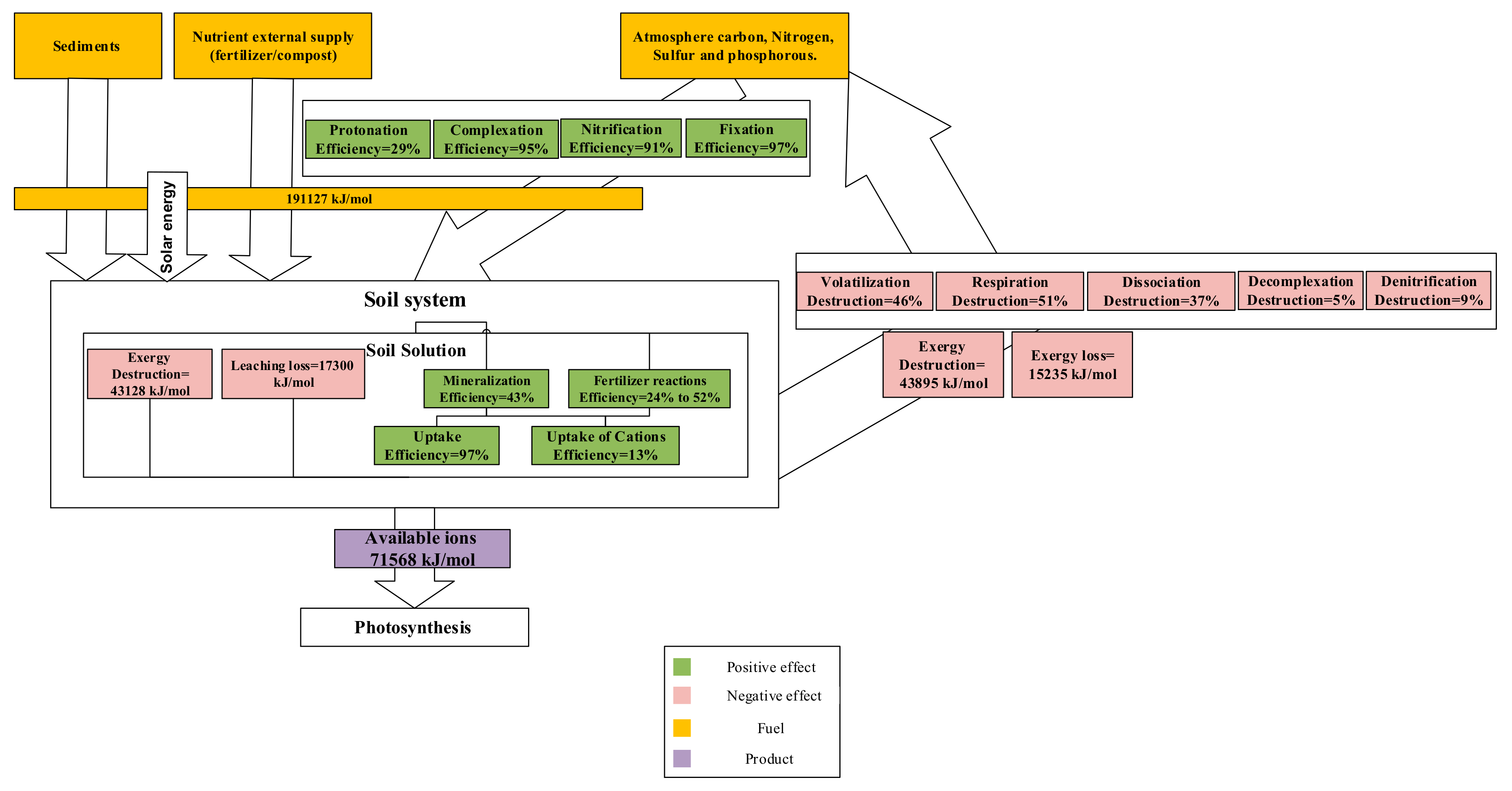
| total | 191,126.90 | 71,568.07 | 32,535.89 | 87,022.94 | 37.45 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bararzadeh Ledari, M.; Saboohi, Y.; Valero, A.; Azamian, S. Exergy Analysis of a Bio-System: Soil–Plant Interaction. Entropy 2021, 23, 3. https://doi.org/10.3390/e23010003
Bararzadeh Ledari M, Saboohi Y, Valero A, Azamian S. Exergy Analysis of a Bio-System: Soil–Plant Interaction. Entropy. 2021; 23(1):3. https://doi.org/10.3390/e23010003
Chicago/Turabian StyleBararzadeh Ledari, Masoomeh, Yadollah Saboohi, Antonio Valero, and Sara Azamian. 2021. "Exergy Analysis of a Bio-System: Soil–Plant Interaction" Entropy 23, no. 1: 3. https://doi.org/10.3390/e23010003
APA StyleBararzadeh Ledari, M., Saboohi, Y., Valero, A., & Azamian, S. (2021). Exergy Analysis of a Bio-System: Soil–Plant Interaction. Entropy, 23(1), 3. https://doi.org/10.3390/e23010003





