Dephasing Process of a Single Atom Interacting with a Two-Mode Field
Abstract
:1. Introduction
2. Model and Solution
3. Numerical Results
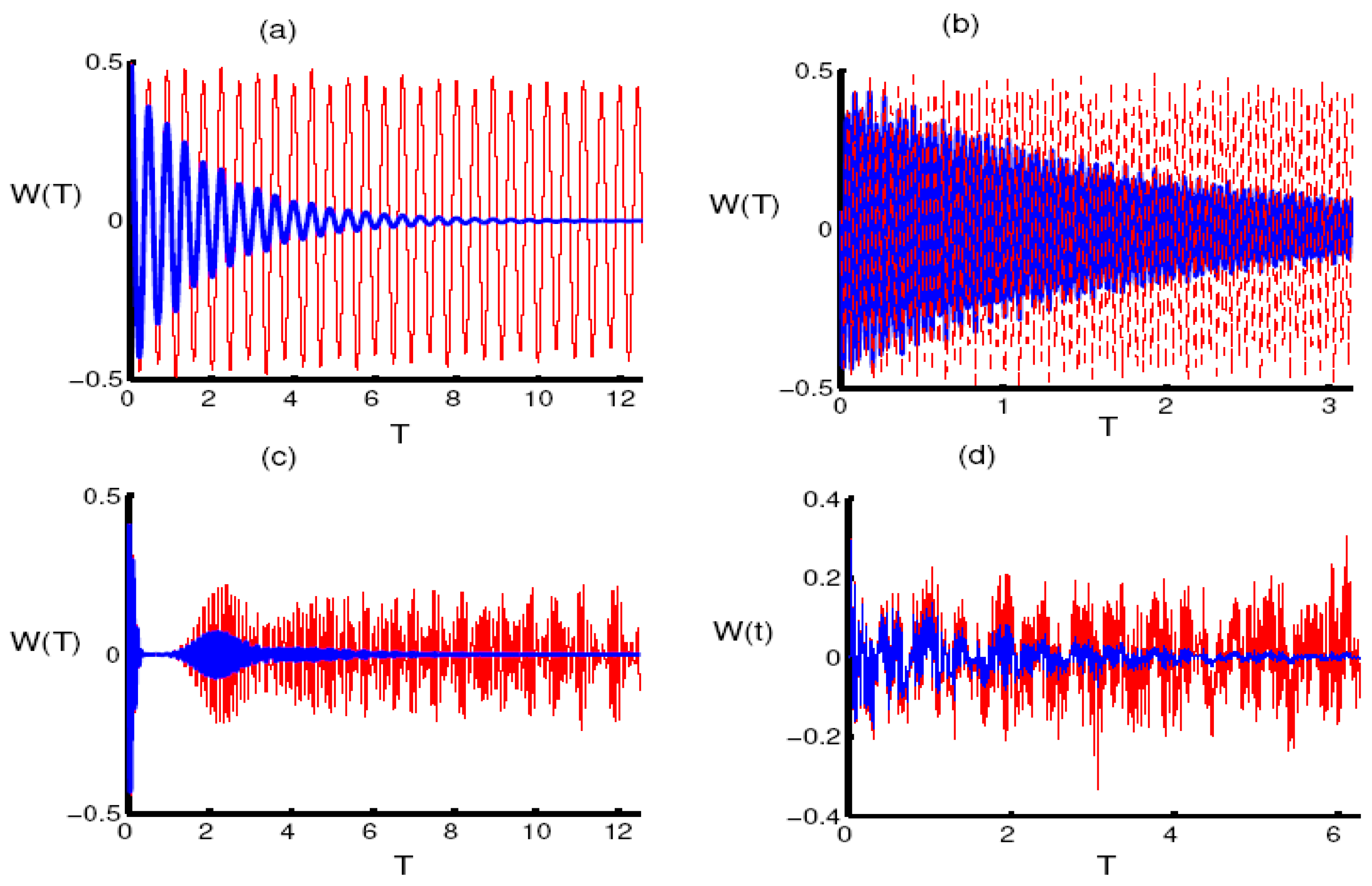
3.1. Population Inversion
3.2. Linear Entropy
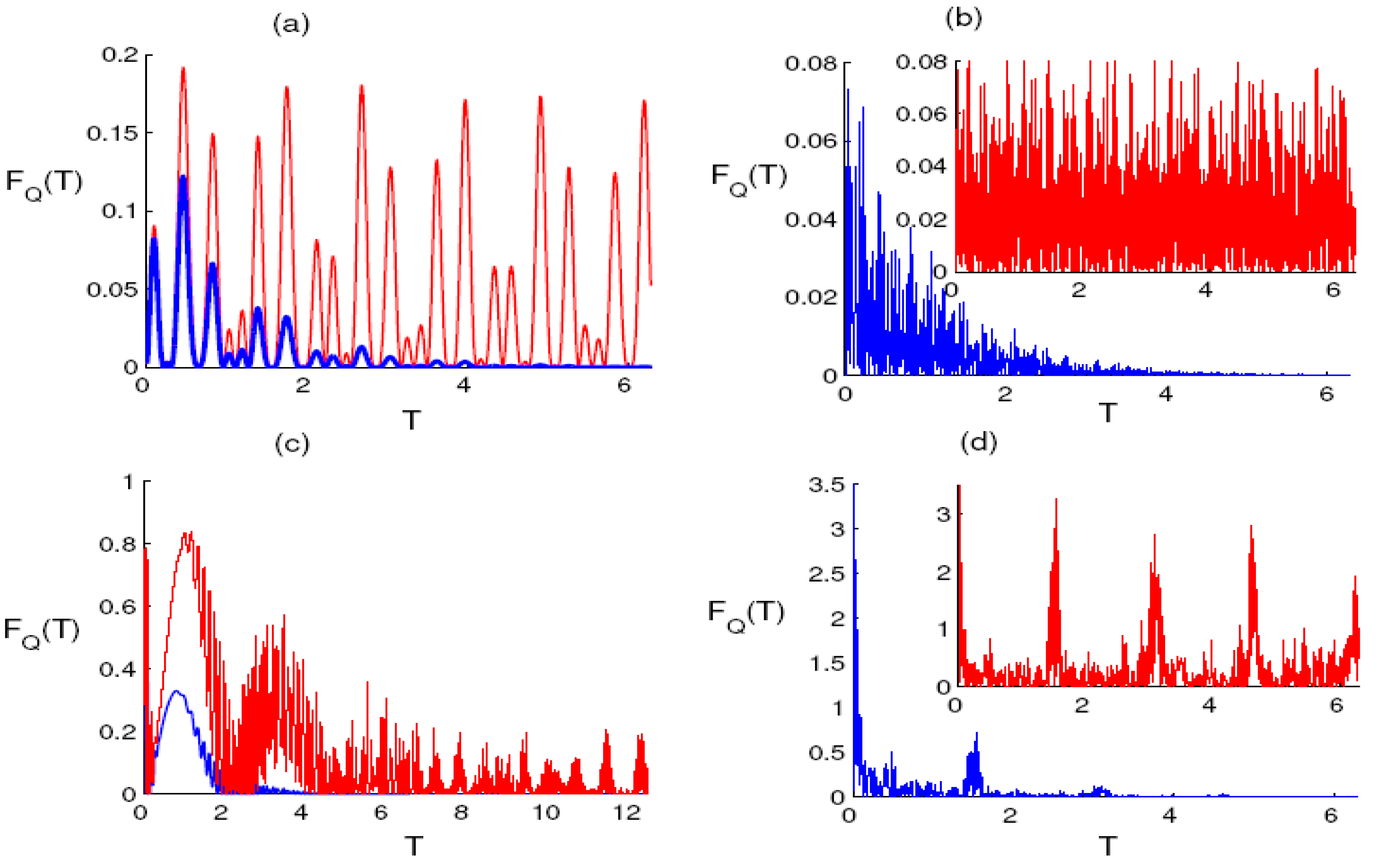
3.3. Quantum Fisher Information
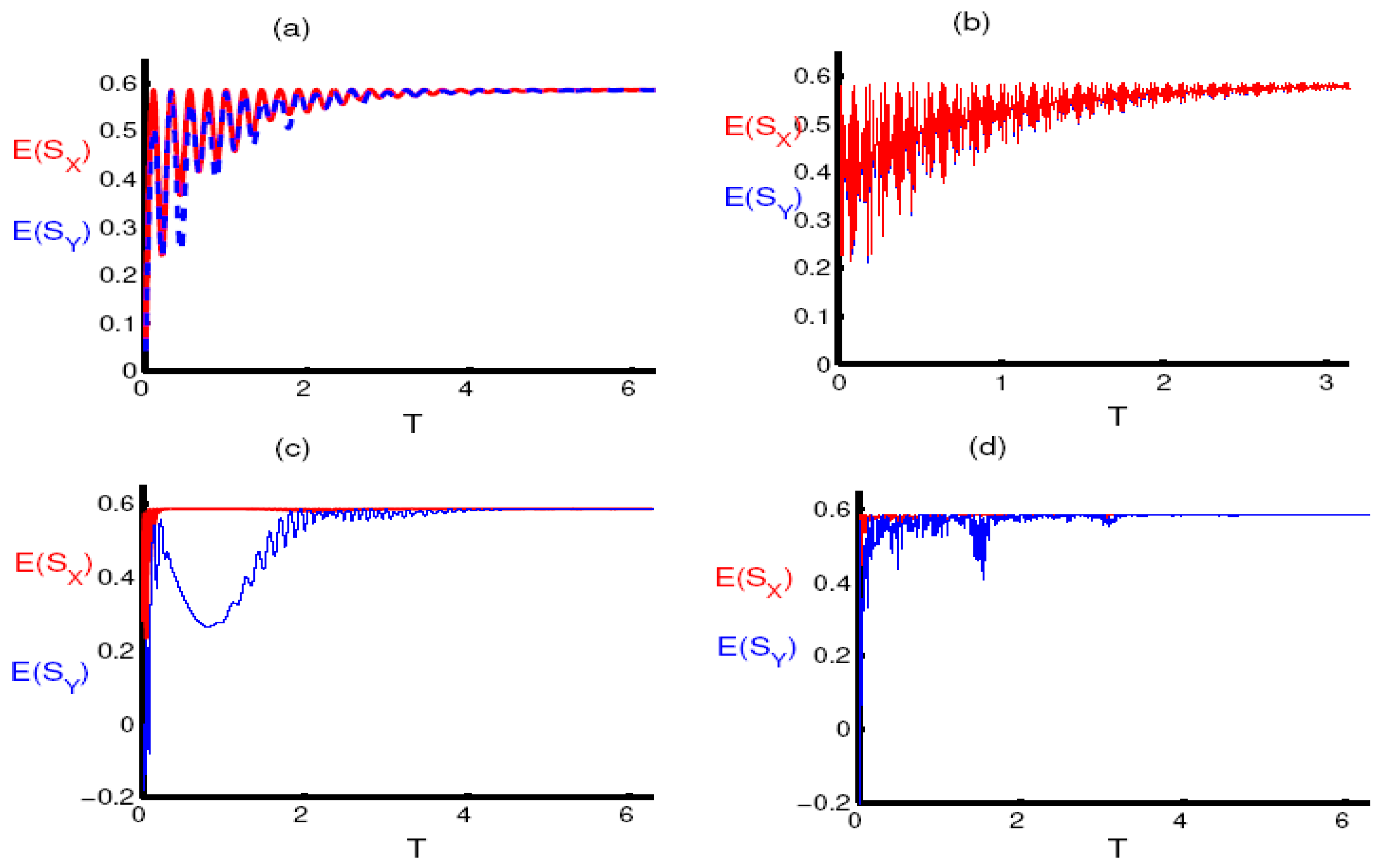
3.4. Squeezing Phenomena
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89. [Google Scholar] [CrossRef] [Green Version]
- Rempe, G.; Walther, H.; Klien, N. Observation of quantum collapse and revival in a one-atom maser. Phys. Rev. Lett. 1987, 57, 353. [Google Scholar] [CrossRef] [PubMed]
- Clark, S.G.; Parkins, A.S. Entanglement and entropy engineering of atomic two-qubit states. Phys. Rev. Lett. 2003, 90, 047905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joshi, G.A. Nonlinear dynamical evolution of the driven two-photon Jaynes-Cummings model. Phys. Rev. A 2000, 62, 043812. [Google Scholar] [CrossRef]
- Eberly, J.H.; Narozhny, N.B.; Sanchez-Mondragan, J.J. Periodic Spontaneous Collapse and Revival in a Simple Quantum Model. Phys. Rev. Lett. 1980, 44, 1323. [Google Scholar] [CrossRef]
- Diedrich, F.; Walther, H. Nonclassical radiation of a single stored ion. Phys. Rev. Lett. 1987, 58, 203. [Google Scholar] [CrossRef]
- Milonni, P.W.; Ackerhalt, J.R.; Galbraith, H.W. Chaos in the semiclassical N-atom Jaynes-Cummings model: Failure of the rotating-wave approximation. Phys. Rev. Lett. 1983, 50, 966. [Google Scholar] [CrossRef]
- Kuklinski, J.R.; Madajczyk, J.L. Strong squeezing in the Jaynes-Cummings model. Phys. Rev. A 1988, 37, 3175. [Google Scholar] [CrossRef] [PubMed]
- Slosser, J.J.; Meystre, P.; Braunstein, S.L. Harmonic oscillator driven by a quantum current. Phys. Rev. Lett. 1990, 63, 934. [Google Scholar] [CrossRef] [PubMed]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Rungta, P.; Puzek, V.; Caves, C.M.; Hillery, H.; Milburn, G.J. Universal state inversion and concurrence in arbitrary dimensions. Phys. Rev. A 2001, 64, 042315. [Google Scholar] [CrossRef] [Green Version]
- Benenti, G.; Casati, G.; Strini, G. Principle of Quantum Computation and Information; World Scientific: Singapore, 2004. [Google Scholar]
- Bashkirov, E.K.; Kien, F.L.; Shumovsky, A.S. Collective spontaneous radiation of two atoms in the finite-Q cavity. Physica A 1990, 167, 935. [Google Scholar] [CrossRef]
- Kim, M.S.; de-Olivera, F.A.M.; Knight, P.L. Simultaneous jumps in two two-level atoms. Opt. Commun. 1989, 70, 473. [Google Scholar] [CrossRef]
- Kim, M.S.; Agarwal, G.S. Cavity-induced two-photon absorption in unidentical atoms. Phys. Rev. A 1998, 57, 3059. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.S.; Lee, J.; Ahn, D.; Knight, P.L. Entanglement induced by a single-mode heat environment. Phys. Rev. A 2002, 65, 040101. [Google Scholar] [CrossRef] [Green Version]
- El-Orany, F.A.A.; Wahiddin, M.R.B.; Obada, A.-S.F. Single-atom entropy squeezing for two two-level atoms interacting with a single-mode radiation field. Opt. Commun. 2008, 281, 2854. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.-Q.; Song, H.-S.; Zhou, L.; Yi, X.-X. Entangling two-atom through cooperative interaction under stimulated emission. Int. J. Theor. Phys. 2006, 45, 2247. [Google Scholar] [CrossRef] [Green Version]
- Ozel, C.; Yilmaz, E.; Kayhan, H.; Aktag, A. Stationary state entanglement of two atoms inside an optical cavity under noise. Int. J. Theor. Phys. 2008, 47, 3101. [Google Scholar] [CrossRef]
- Von Neumann, J. Mathematische Grundlagen der Quantenmechanik; Springer: Berlin/Heidelberg, Germany, 1932. [Google Scholar]
- Anaya-Contreras, J.A.; Zúñiga-Segundo, A.; Moya-Cessa, H.M. Entropy fluctuations to quantify mixedness. Int. J. Quantum Inf. 2019, 17, 1941007. [Google Scholar] [CrossRef]
- Phoenix, S.J.D. Wave-packet evolution in the damped oscillator. Phys. Rev. A 1990, 41, 5132. [Google Scholar] [CrossRef]
- Phoenix, S.J.D.; Knight, P.L. Fluctuations and entropy in models of quantum optical resonance. Ann. Phys. 1988, 186, 381. [Google Scholar] [CrossRef]
- Barnett, S.M.; Beige, A.; Ekert, A.; Garraway, B.M.; Keitel, C.H.; Kendon, V.; Lein, M.; Milburn, G.J.; Moya-Cessa, H.M.; Murao, M.; et al. Journeys from quantum optics to quantum technology. Progr. Quant. Elec. 2017, 54, 19. [Google Scholar] [CrossRef]
- Pathak, A. Elements of Quantum Computation and Quantum Communication; CRC Press: New York, NY, USA, 2013. [Google Scholar]
- Wineland, D.J.; Bollinger, J.J.; Itano, W.M. Squeezed atomic states and projection noise in spectroscopy. Phys. Rev. A 1994, 50, 67. [Google Scholar] [CrossRef]
- Kitagawa, M.; Ueda, M. Squeezed spin states. Phys. Rev. A 1993, 47, 5138. [Google Scholar] [CrossRef]
- Walls, D.F.; Zoller, P. Reduced quantum fluctuations in resonance fluorescence. Phys. Rev. Lett. 1981, 47, 709. [Google Scholar] [CrossRef]
- Sorensen, J.L.; Hald, J.; Polzik, E.S. Quantum noise of an atomic spin polarization measurement. Phys. Rev. Lett. 1998, 80, 3487. [Google Scholar] [CrossRef]
- Wodkiewicz, K. Reduced quantum fluctuations in the Josephson junction. Phys. Rev. B 1985, 32, 4750. [Google Scholar] [CrossRef] [PubMed]
- Ashraf, M.M.; Razmi, M.S.K. Atomic-dipole squeezing and emission spectra of the nondegenerate two-photon Jaynes-Cummings model. Phys. Rev. A 1992, 45, 8121. [Google Scholar] [CrossRef] [PubMed]
- Kuzmicah, A.; Molmer, K.; Polzik, E.S. Spin squeezing in an ensemble of atoms illuminated with squeezed light. Phys. Rev. Lett. 1997, 79, 4782. [Google Scholar] [CrossRef]
- Sairo, H.; Ueda, M. Quantum-controlled few-photon state generated by squeezed atoms. Phys. Rev. Lett. 1997, 79, 3869. [Google Scholar]
- Pirandola, S.; Bardhan, B.R.; Gehring, T.; Weedbrook, C.; Lloyd, S. Advances in photonic quantum sensing. Nat. Photon. 2018, 12, 724. [Google Scholar] [CrossRef]
- Huelga, S.F.; Macchiavello, C.; Pellizzari, T.; Ekert, A.K.; Plenio, M.B.; Cirac, J.I. Improvement of frequency standards with quantum entanglement. Phys. Rev. Lett. 1997, 79, 3865. [Google Scholar] [CrossRef] [Green Version]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum-enhanced measurements: Beating the standard quantum limit. Science 2004, 306, 1330. [Google Scholar] [CrossRef] [Green Version]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Quantum metrology. Phys. Rev. Lett. 2006, 96, 010401. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giovannetti, V.; Lloyd, S.; Maccone, L. Advances in quantum metrology. Nat. Photon. 2011, 5, 222. [Google Scholar] [CrossRef]
- Abdel-Khalek, S. Quantum Fisher information flow and entanglement in pair coherent states. Opt. Quantum Eletronics 2014, 46, 1055. [Google Scholar] [CrossRef]
- Chin, A.W.; Huelga, S.F.; Plenio, M.B. Quantum metrology in non-Markovian environments. Phys. Rev. Lett. 2012, 109, 233601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Demkowicz-Dobrzański, R.; Koaodyński, J.; Guţ, M. The elusive Heisenberg limit in quantum-enhanced metrology. Nat. Commun. 2012, 3, 1063. [Google Scholar] [CrossRef] [Green Version]
- Chaves, R.; Brask, J.; Markiewicz, M.; Koaodyński, J.; Acan, A. Noisy metrology beyond the standard quantum limit. Phys. Rev. Lett. 2013, 111, 120401. [Google Scholar] [CrossRef]
- Berrada, K. Non-Markovian effect on the precision of parameter estimation. Phys. Rev. A 2013, 88, 035806. [Google Scholar] [CrossRef]
- Lu, X.-M.; Yu, S.; Oh, C. Robust quantum metrological schemes based on protection of quantum Fisher information. Nat. Commun. 2015, 6, 7282. [Google Scholar] [CrossRef]
- Li, Y.-L.; Xiao, X.; Yao, Y. Classical-driving-enhanced parameter-estimation precision of a non-Markovian dissipative two-state system. Phys. Rev. A 2015, 91, 052105. [Google Scholar] [CrossRef] [Green Version]
- Berrada, K.J. Protecting the precision of estimation in a photonic crystal. Opt. Soc. Am. B 2015, 32, 571. [Google Scholar] [CrossRef]
- Liu, J.; Yuan, H. Quantum parameter estimation with optimal control. Phys. Rev. A 2017, 96, 012117. [Google Scholar] [CrossRef] [Green Version]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- Entezar, S.R.J. Controllable atom–photon entanglement near a 3D anisotropic photonic band edge. Phys. B Atom. Mol. Opt. Phys. 2010, 43, 085503. [Google Scholar] [CrossRef]
- Mortezapour, A.; Abedi, M.; Mahmoudi, M.; Khajehpour, M.R.H.J. The effect of a coupling field on the entanglement dynamics of a three-level atom. Phys. B Atom. Mol. Opt. Phys. 2011, 44, 085501. [Google Scholar] [CrossRef] [Green Version]
- Mortezapour, A.; Kordi, Z.; Mahmoudi, M. Phase-controlled atom—photon entanglement in a three-level Λ—type closed-loop atomic system. Chin. Phys. B 2013, 22, 060310. [Google Scholar] [CrossRef]
- Abazari, M.; Mortezapour, A.; Mahmoudi, M.; Sahrai, M. Phase-controlled atom-photon entanglement in a three-level V-type atomic system via spontaneously generated coherence. Entropy 2011, 13, 1541. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Yan, D.; Bao, Q.; Zhang, Y.; Cui, C. The influence of spontaneously generated coherence on atom-photon entanglement in a Λ-type system with an incoherent pump. Open Phys. 2014, 12, 813. [Google Scholar] [CrossRef] [Green Version]
- Gholipour, H.; Mortezapour, A.; Nosrati, F.; Lo Franco, R. Quantumness and memory of one qubit in a dissipative cavity under classical control. Ann. Phys. 2020, 441, 168073. [Google Scholar] [CrossRef] [Green Version]
- Rosenfeld, W.; Berner, S.; Volz, J.; Weber, M.; Weinfurter, H. Remote preparation of an atomic quantum memory. Phys. Rev. Lett. 2007, 98, 050504. [Google Scholar] [CrossRef] [Green Version]
- Briegel, H.-J.; Dar, W.; Cirac, J.I.; Zoller, P. Quantum repeaters: The role of imperfect local operations in quantum communication. Phys. Rev. Lett. 1998, 81, 5932. [Google Scholar] [CrossRef]
- Yuan, Z.-S.; Chen, Y.-A.; Zhao, B.; Chen, S.; Schmiedmayer, J.; Pan, J.-W. Experimental demonstration of a BDCZ quantum repeater node. Nature 2008, 454, 1098. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ferraro, E.; Napoli, A.; Guccione, M.; Messina, A. Entanglement sudden death and sudden birth in two uncoupled spins. Phys. Scr. T. 2009, 135, 014032. [Google Scholar] [CrossRef] [Green Version]
- Breuer, H.-P.; Burgarth, D.; Petruccione, F. Non-Markovian dynamics in a spin star system: Exact solution and approximation techniques. Phys. Rev. B 2004, 70, 045323. [Google Scholar] [CrossRef] [Green Version]
- Hutton, A.; Bose, S. Mediated entanglement and correlations in a star network of interacting spins. Phys. Rev. A 2003, 69, 042312. [Google Scholar] [CrossRef] [Green Version]
- El-Orany, F.A.A.; Sebawe Abdalla, M.J. Variance squeezing and entanglement of the XX central spin model. Phys. A Math. Theor. 2011, 44, 035302. [Google Scholar] [CrossRef] [Green Version]
- Schwinger, J. Quantum Theory of Angular Momentum; Biedenharn, L., van Dam, H., Eds.; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Obada, A.-S.F.; Khalil, E.M. Generation and some non-classical properties of a finite dimensional pair coherent state. Opt. Commun. 2006, 260, 19. [Google Scholar] [CrossRef]
- Ban, M. Quantum master equation for dephasing of a two-level system with an initial correlation. Phys. Rev. A 2009, 80, 064103. [Google Scholar] [CrossRef]
- Maassen, H.; Uffink, J.B.M. Generalized entropic uncertainty relations. Phys. Rev. Lett. 1988, 60, 1103. [Google Scholar] [CrossRef] [PubMed]
- Fang, M.F.; Peng, Z.; Swain, S. Entropy squeezing for a two-level atom. J. Mod. Optics 2000, 47, 1043. [Google Scholar] [CrossRef]
- Abdalla, M.S.; Obada, A.-S.F.; Adel-Khalek, S. Entropy squeezing of time dependent single-mode Jaynes–Cummings model in presence of non-linear effect. Chaos Solitons Fractals 2008, 36, 405. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalil, E.M.; Berrada, K.; Abdel-Khalek, S.; Alsubei, B.; Eleuch, H. Dephasing Process of a Single Atom Interacting with a Two-Mode Field. Entropy 2021, 23, 252. https://doi.org/10.3390/e23020252
Khalil EM, Berrada K, Abdel-Khalek S, Alsubei B, Eleuch H. Dephasing Process of a Single Atom Interacting with a Two-Mode Field. Entropy. 2021; 23(2):252. https://doi.org/10.3390/e23020252
Chicago/Turabian StyleKhalil, Eied M., Kamal Berrada, Sayed Abdel-Khalek, Beida Alsubei, and Hichem Eleuch. 2021. "Dephasing Process of a Single Atom Interacting with a Two-Mode Field" Entropy 23, no. 2: 252. https://doi.org/10.3390/e23020252





