Non-Extensive Statistical Analysis of Acoustic Emissions: The Variability of Entropic Index q during Loading of Brittle Materials Until Fracture
Abstract
:1. Introduction
2. Theoretical Background
3. Specimens
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sammonds, P.R.; Meredith, P.G.; Main, I.G. Role of pore fluids in the generation of seismic precursors to shear fracture. Nature 1992, 359, 228–230. [Google Scholar] [CrossRef]
- Shiotani, T. Evaluation of progressive failure using AE sources and improved b-value on slope model tests. Prog. Acoust. Emiss. VII JSNDI 1994, 7, 529–534. [Google Scholar]
- Colombo, I.S.; Main, I.G.; Forde, M.C. Assessing Damage of Reinforced Concrete Beam Using “b-value” Analysis of Acoustic Emission Signals. J. Mater. Civ. Eng. 2003, 15, 280–286. [Google Scholar] [CrossRef] [Green Version]
- Triantis, D.; Kourkoulis, S.K. An Alternative Approach for Representing the Data Provided by the Acoustic Emission Technique. Rock Mech. Rock Eng. 2018, 51, 2433–2438. [Google Scholar] [CrossRef]
- Loukidis, A.; Pasiou, E.D.; Sarlis, N.V.; Triantis, D. Fracture analysis of typical construction materials in natural time. Phys. A Stat. Mech. Appl. 2019, 123831. [Google Scholar] [CrossRef]
- Ohtsu, M.; Uchida, M.; Okamoto, T.; Yuyama, S. Damage Assessment of Reinforced Concrete Beams Qualified by Acoustic Emission. ACI Struct. J. 2002, 99. [Google Scholar] [CrossRef]
- Holford, K.M. Acoustic Emission in Structural Health Monitoring. Key Eng. Mater. 2009, 413–414, 15–28. [Google Scholar] [CrossRef]
- Kourkoulis, S.K.; Ganniari-Papageorgiou, E.; Mentzini, M. Dionysos marble beams under bending: A contribution towards understanding the fracture of the Parthenon architraves. Eng. Geol. 2010, 115, 246–256. [Google Scholar] [CrossRef]
- Lacidogna, G.; Manuello, A.; Niccolini, G.; Carpinteri, A. Acoustic emission monitoring of Italian historical buildings and the case study of the Athena temple in Syracuse. Archit. Sci. Rev. 2015, 58, 290–299. [Google Scholar] [CrossRef]
- Main, I.; Meredith, P.; Jones, C. A reinterpretation of the precursory seismic b-value anomaly from fracture mechanics. Geophys. J. Int. 1989, 96, 131–138. [Google Scholar] [CrossRef]
- Shiotani, T.; Yuyama, S.; Li, Z.W.; Ohtsu, M. Application of AE improved b-value to quantitative evaluation of fracture process in concrete materials. J. Acoust. Emiss. 2001, 19, 118–133. [Google Scholar]
- Rao, M.V.M.S.; Lakshmi, K.J.P. Analysis of b-value and improved b-value of acoustic emissions accompanying rock fracture. Curr. Sci. 2005, 89, 1577–1582. [Google Scholar]
- Sagar, R.V.; Prasad, B.K.R.; Kumar, S.S. An experimental study on cracking evolution in concrete and cement mortar by the b-value analysis of acoustic emission technique. Cem. Concr. Res. 2012, 42, 1094–1104. [Google Scholar] [CrossRef]
- Hirata, T. Omori’s Power Law aftershock sequences of microfracturing in rock fracture experiment. J. Geophys. Res. Solid Earth 1987, 92, 6215–6221. [Google Scholar] [CrossRef]
- Meredith, P.G.; Main, I.G.; Jones, C. Temporal variations in seismicity during quasi-static and dynamic rock failure. Tectonophysics 1990, 175, 249–268. [Google Scholar] [CrossRef]
- Cox, S.J.D.; Meredith, P.G. Microcrack formation and material softening in rock measured by monitoring acoustic emissions. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1993, 30, 11–24. [Google Scholar] [CrossRef]
- Benson, P.M.; Vinciguerra, S.; Meredith, P.G.; Young, R.P. Laboratory Simulation of Volcano Seismicity. Science 2008, 322, 249. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jiaying, C.; Xudong, Z.; Linmei, Y.; Fenng, W. The vacancy defects and oxygen atoms occupation effects on mechanical and electronic properties of Mo5Si3 silicides. Commun. Theor. Phys. 2021. [Google Scholar] [CrossRef]
- Zhang, X.; Dong, T.; Ma, H.; Li, D.; Ying, C.; Liu, C.; Wang, F. A first principles investigation on the influence of transition-metal elements on the structural, mechanical, and anisotropic properties of CaM2Al20 intermetallics. J. Mol. Graph. Model. 2020, 96, 107509. [Google Scholar] [CrossRef]
- Mai, Z.; Zhang, X.; Liu, Y.; Yu, H.; Wang, F. Insight into the structure dependence on physical properties of the high temperature ceramics TaB2 boride. Vacuum 2020, 177, 109427. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C.; Baldovin, F.; Cerbino, R.; Pierobon, P. Introduction to Nonextensive Statistical Mechanics and Thermodynamics. Phys. Complex Syst. 2003, 155, 229–252. [Google Scholar]
- Tsallis, C. Nonadditive entropy and nonextensive statistical mechanics -an overview after 20 years. Braz. J. Phys. 2009, 39, 337–356. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef] [Green Version]
- Tsallis, C.; Brigatti, E. Nonextensive statistical mechanics: A brief introduction. Contin. Mech. Thermodyn. 2004, 16, 223–235. [Google Scholar] [CrossRef] [Green Version]
- Abe, S.; Suzuki, N. Law for the distance between successive earthquakes. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef] [Green Version]
- Abe, S.; Suzuki, N. Scale-free statistics of time interval between successive earthquakes. Phys. A Stat. Mech. Appl. 2005, 350, 588–596. [Google Scholar] [CrossRef] [Green Version]
- Hasumi, T. Interoccurrence time statistics in the two-dimensional Burridge-Knopoff earthquake model. Phys. Rev. E 2007, 76, 026117. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Darooneh, A.H.; Dadashinia, C. Analysis of the spatial and temporal distributions between successive earthquakes: Nonextensive statistical mechanics viewpoint. Phys. A Stat. Mech. Appl. 2008, 387, 3647–3654. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. Is plate tectonics a case of non-extensive thermodynamics? Phys. A Stat. Mech. Appl. 2010, 389, 4989–4993. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Nonextensivity and natural time: The case of seismicity. Phys. Rev. E 2010, 82, 021110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vallianatos, F.; Sammonds, P. A non-extensive statistics of the fault-population at the Valles Marineris extensional province, Mars. Tectonophysics 2011, 509, 50–54. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G.; Tzanis, A. Evidence of non-extensivity in the seismicity observed during the 2011-2012 unrest at the Santorini volcanic complex, Greece. Nat. Hazards Earth Syst. Sci. 2013, 13, 177–185. [Google Scholar] [CrossRef] [Green Version]
- Vallianatos, F.; Sammonds, P. Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran–Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 2013, 590, 52–58. [Google Scholar] [CrossRef]
- Vallianatos, F.; Michas, G.; Papadakis, G. Non-extensive and natural time analysis of seismicity before the Mw6.4, October 12, 2013 earthquake in the South West segment of the Hellenic Arc. Phys. A Stat. Mech. Appl. 2014, 414, 163–173. [Google Scholar] [CrossRef]
- Vallianatos, F.; Benson, P.; Meredith, P.; Sammonds, P. Experimental evidence of a non-extensive statistical physics behaviour of fracture in triaxially deformed Etna basalt using acoustic emissions. EPL (Europhys. Lett.) 2012, 97, 58002. [Google Scholar] [CrossRef]
- Stergiopoulos, C.; Stavrakas, I.; Hloupis, G.; Triantis, D.; Vallianatos, F. Electrical and Acoustic Emissions in cement mortar beams subjected to mechanical loading up to fracture. Eng. Fail. Anal. 2013, 35, 454–461. [Google Scholar] [CrossRef]
- Stavrakas, I.; Triantis, D.; Kourkoulis, S.K.; Pasiou, E.D.; Dakanali, I. Acoustic Emission Analysis of Cement Mortar Specimens During Three Point Bending Tests. Lat. Am. J. Solids Struct. 2016, 13, 2283–2297. [Google Scholar] [CrossRef] [Green Version]
- Saltas, V.; Vallianatos, F.; Triantis, D.; Stavrakas, I. 8—Complexity in Laboratory Seismology: From Electrical and Acoustic Emissions to Fracture. In Complexity of Seismic Time Series; Chelidze, T., Vallianatos, F., Telesca, L., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 239–273. [Google Scholar] [CrossRef]
- Saltas, V.; Vallianatos, F.; Triantis, D.; Koumoudeli, T.; Stavrakas, I. Non-extensive statistical analysis of acoustic emissions series recorded during the uniaxial compression of brittle rocks. Phys. A Stat. Mech. Appl. 2019, 528, 121498. [Google Scholar] [CrossRef]
- Greco, A.; Tsallis, C.; Rapisarda, A.; Pluchino, A.; Fichera, G.; Contrafatto, L. Acoustic emissions in compression of building materials: Q-statistics enables the anticipation of the breakdown point. Eur. Phys. J. Spec. Top. 2020, 229, 841–849. [Google Scholar] [CrossRef]
- Loukidis, A.; Triantis, D.; Stavrakas, I. Non-Extensive Statistical Analysis of Acoustic Emissions Recorded in Marble and Cement Mortar Specimens Under Mechanical Load Until Fracture. Entropy 2020, 22, 1115. [Google Scholar] [CrossRef]
- Kourkoulis, S.K.; Exadaktylos, G.E.; Vardoulakis, I. U-Notched Dionysos-Pentelicon Marble Beams in Three Point Bending: The Effect of Nonlinearity, Anisotropy and Microstructure. Int. J. Fract. 1999, 98, 369–392. [Google Scholar] [CrossRef]
- Exadaktylos, G.E.; Vardoulakis, I.; Kourkoulis, S.K. Influence of nonlinearity and double elasticity on flexure of rock beams–II. Characterization of Dionysos marble. Int. J. Solids Struct. 2001, 38, 4119–4145. [Google Scholar] [CrossRef]
- Perdikatsis, V.; Kritsotakis, K.; Markopoulos, T.; Laskaridis, K. Petrography, Fabric and Properties. In Fracture and Failure of Natural Building Stones: Applications in the Restoration of Ancient Monuments; Kourkoulis, S.K., Ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 497–515. [Google Scholar] [CrossRef]
- Young, J.F. Portland Cements. In Encyclopedia of Materials: Science and Technology; Buschow, K.H.J., Cahn, R.W., Flemings, M.C., Ilschner, B., Kramer, E.J., Mahajan, S., Veyssière, P., Eds.; Elsevier: Oxford, UK, 2001; pp. 7768–7773. [Google Scholar] [CrossRef]
- Kourkoulis, S.K.; Pasiou, E.D.; Dakanali, I.; Stavrakas, I.; Triantis, D. Mechanical response of notched marble beams under bending versus acoustic emissions and electric activity. J. Theor. Appl. Mech. 2018, 56, 523–547. [Google Scholar] [CrossRef]
- Kourkoulis, S.K.; Pasiou, E.D.; Dakanali, I.; Stavrakas, I.; Triantis, D. Notched marble plates under tension: Detecting prefailure indicators and predicting entrance to the “critical stage”. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 776–786. [Google Scholar] [CrossRef]
- Markides, C.F.; Pasiou, E.D.; Kourkoulis, S.K. A preliminary study on the potentialities of the Circular Semi-Ring test. Procedia Struct. Integr. 2018, 9, 108–115. [Google Scholar] [CrossRef]
- Loukidis, A.; Pasiou, E.D.; Sarlis, N.V.; Triantis, D. Similarity of fluctuations of acoustic emissions in natural time. Procedia Struct. Integr. 2020, 25, 195–200. [Google Scholar] [CrossRef]
- Stergiopoulos, C.; Stavrakas, I.; Triantis, D.; Vallianatos, F.; Stonham, J. Predicting fracture of mortar beams under three-point bending using non-extensive statistical modeling of electric emissions. Phys. A Stat. Mech. Appl. 2015, 419, 603–611. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables; Dover Publications, Inc.: New York, NY, USA, 1965. [Google Scholar]
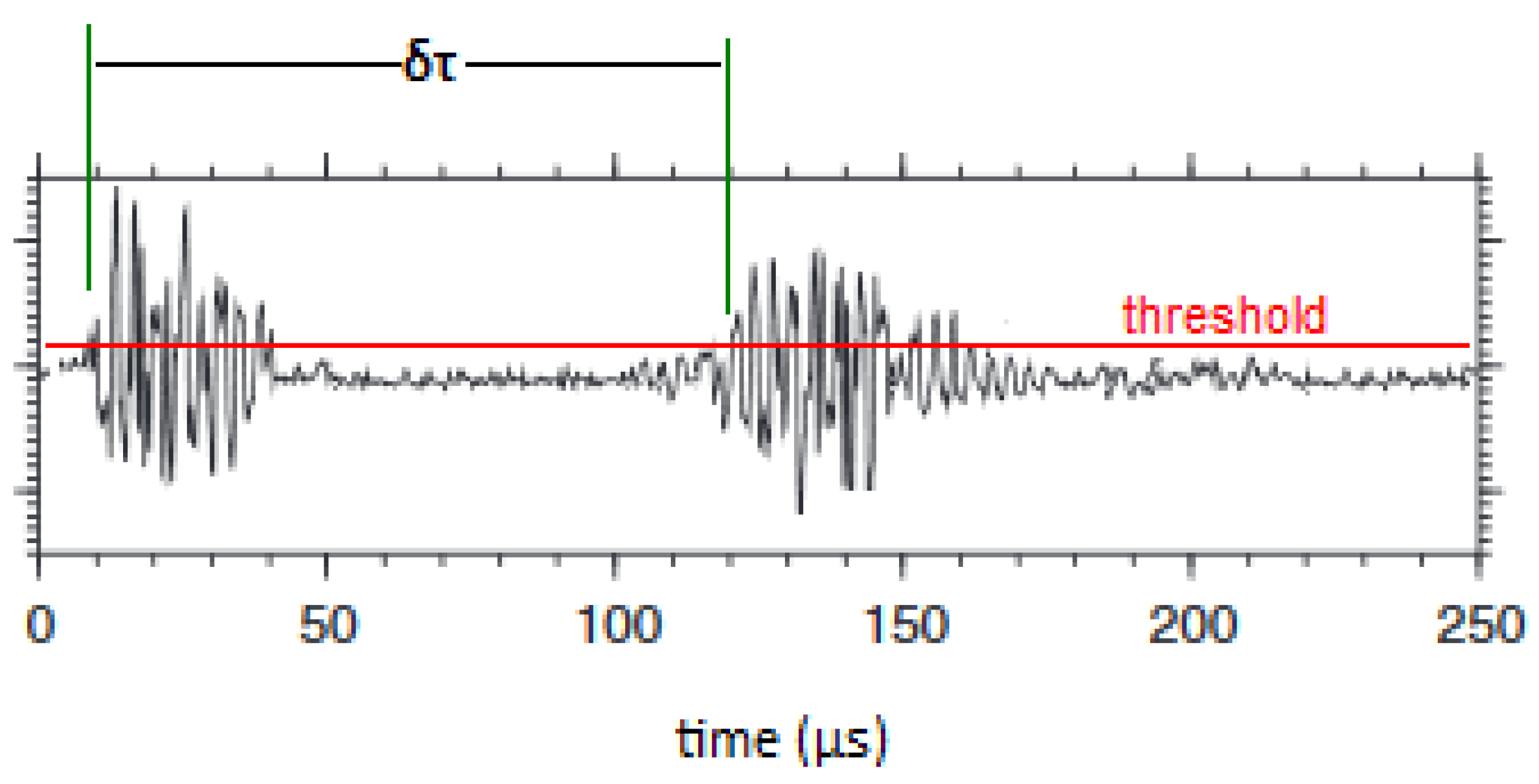

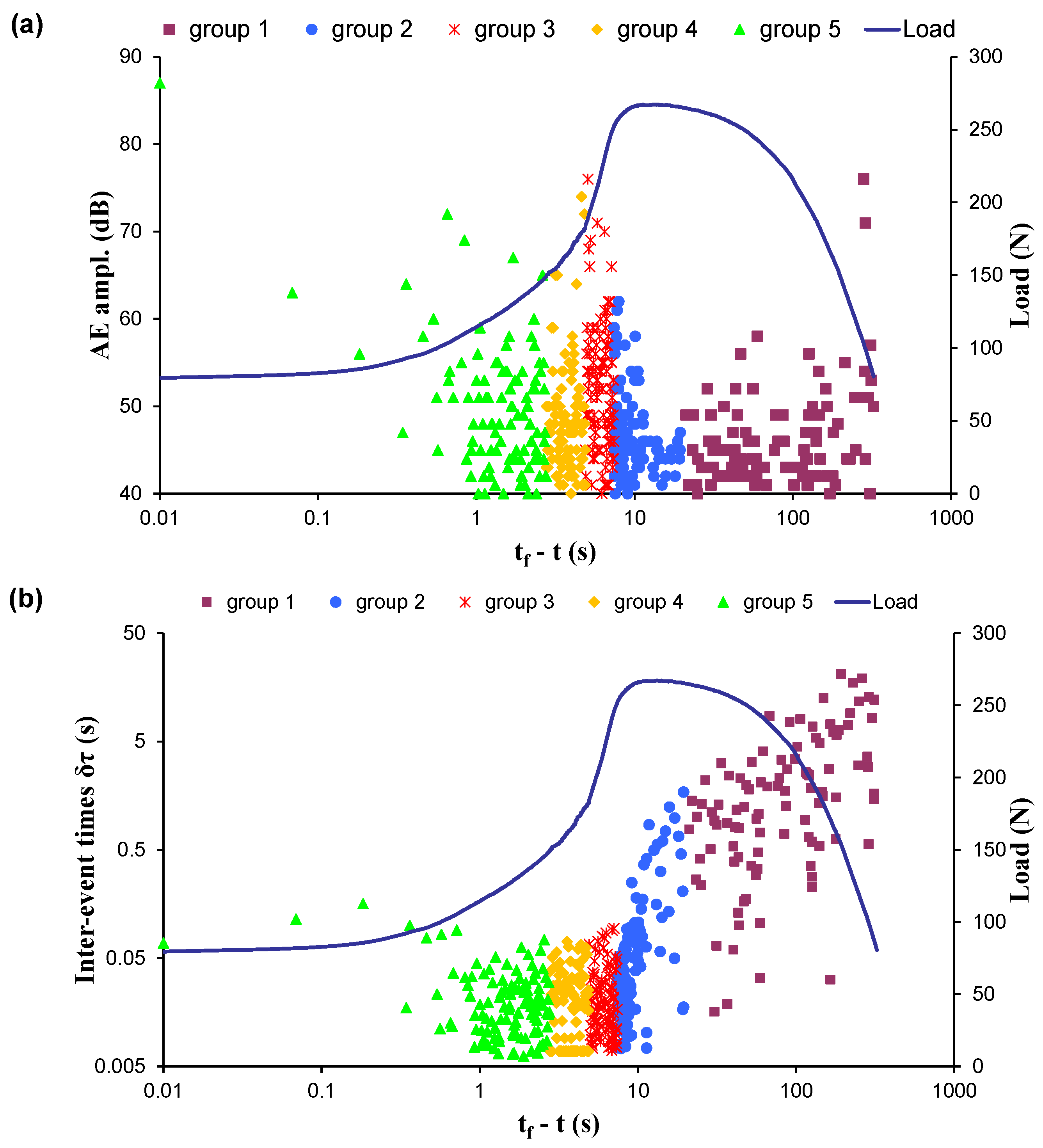
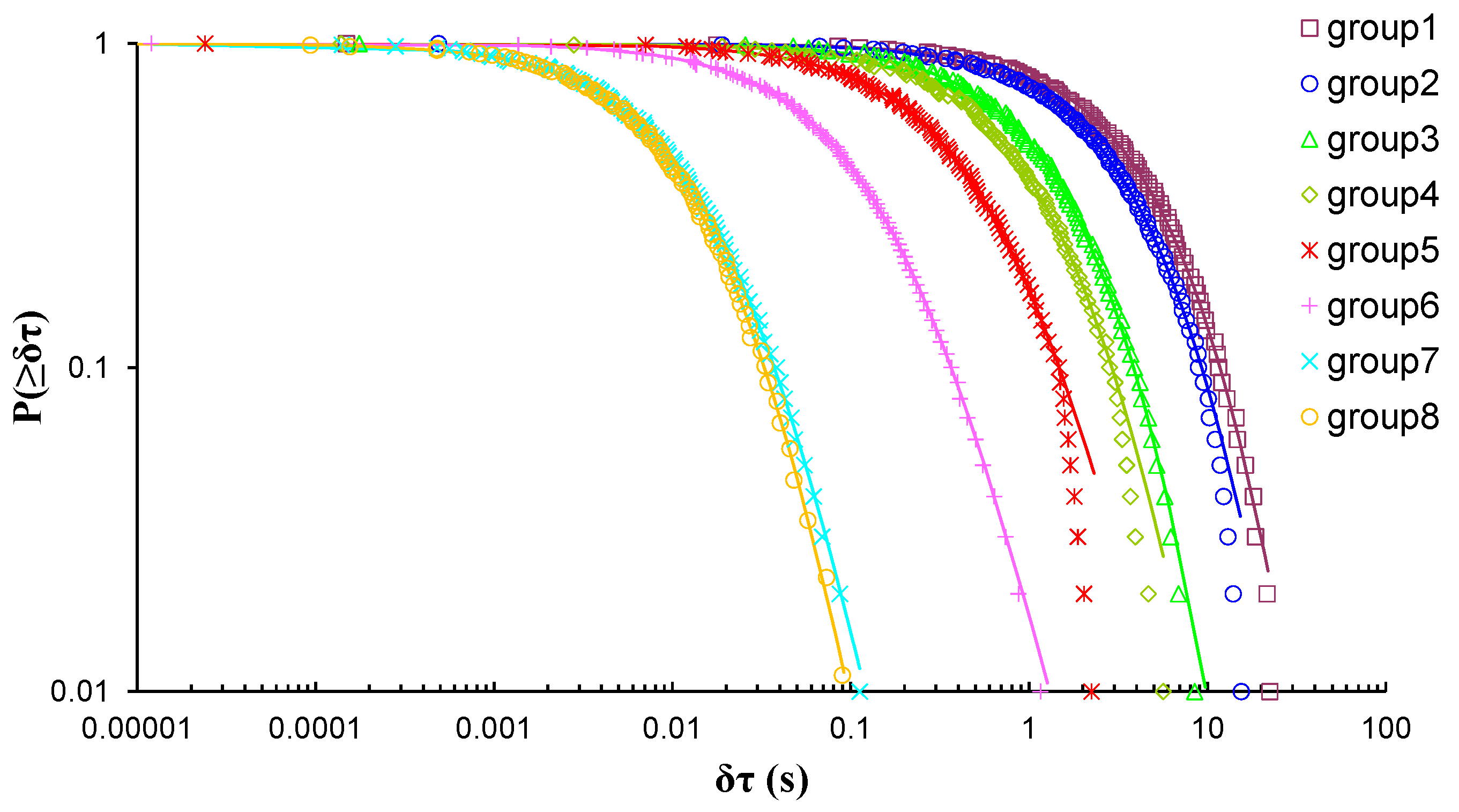
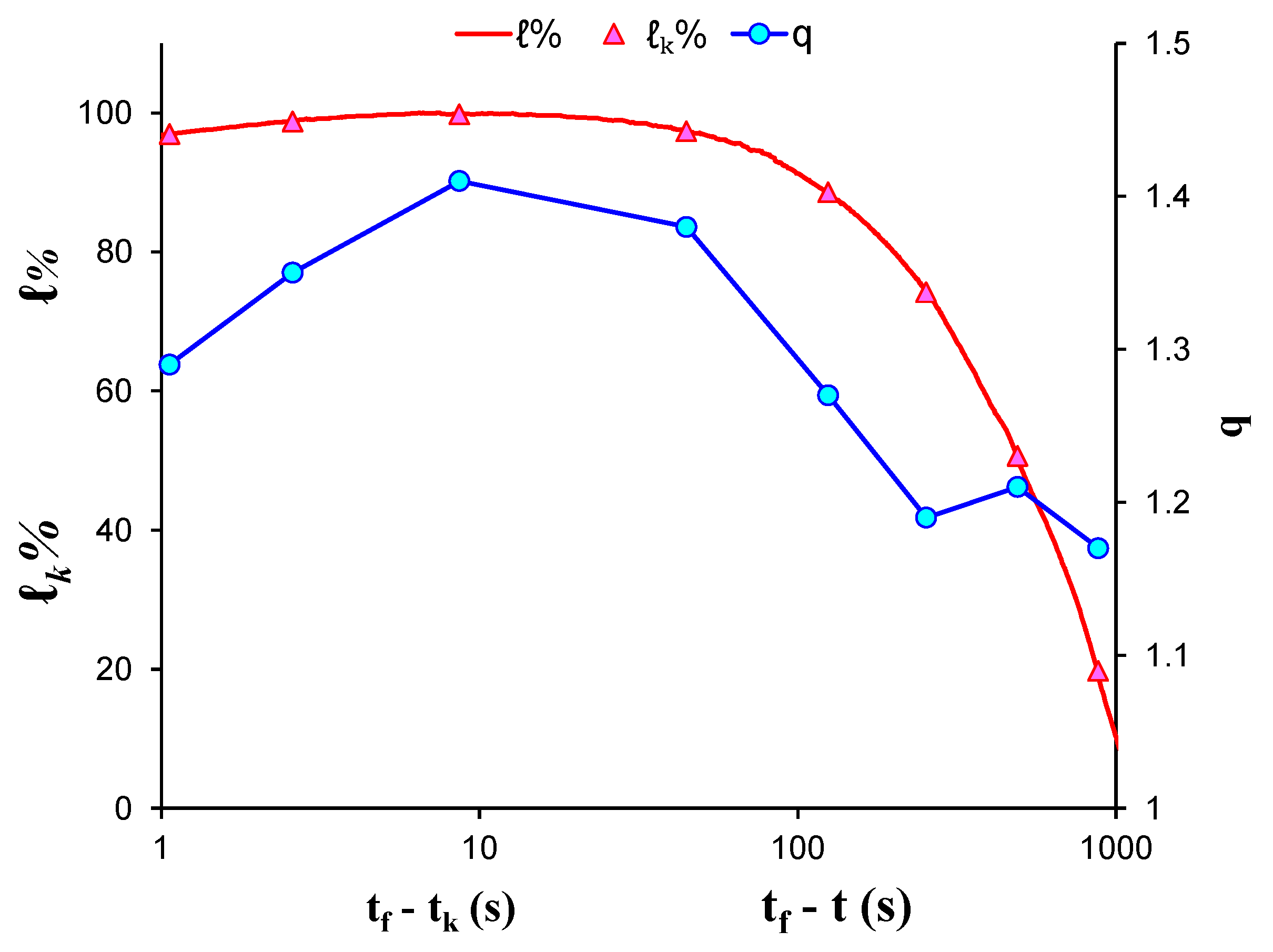
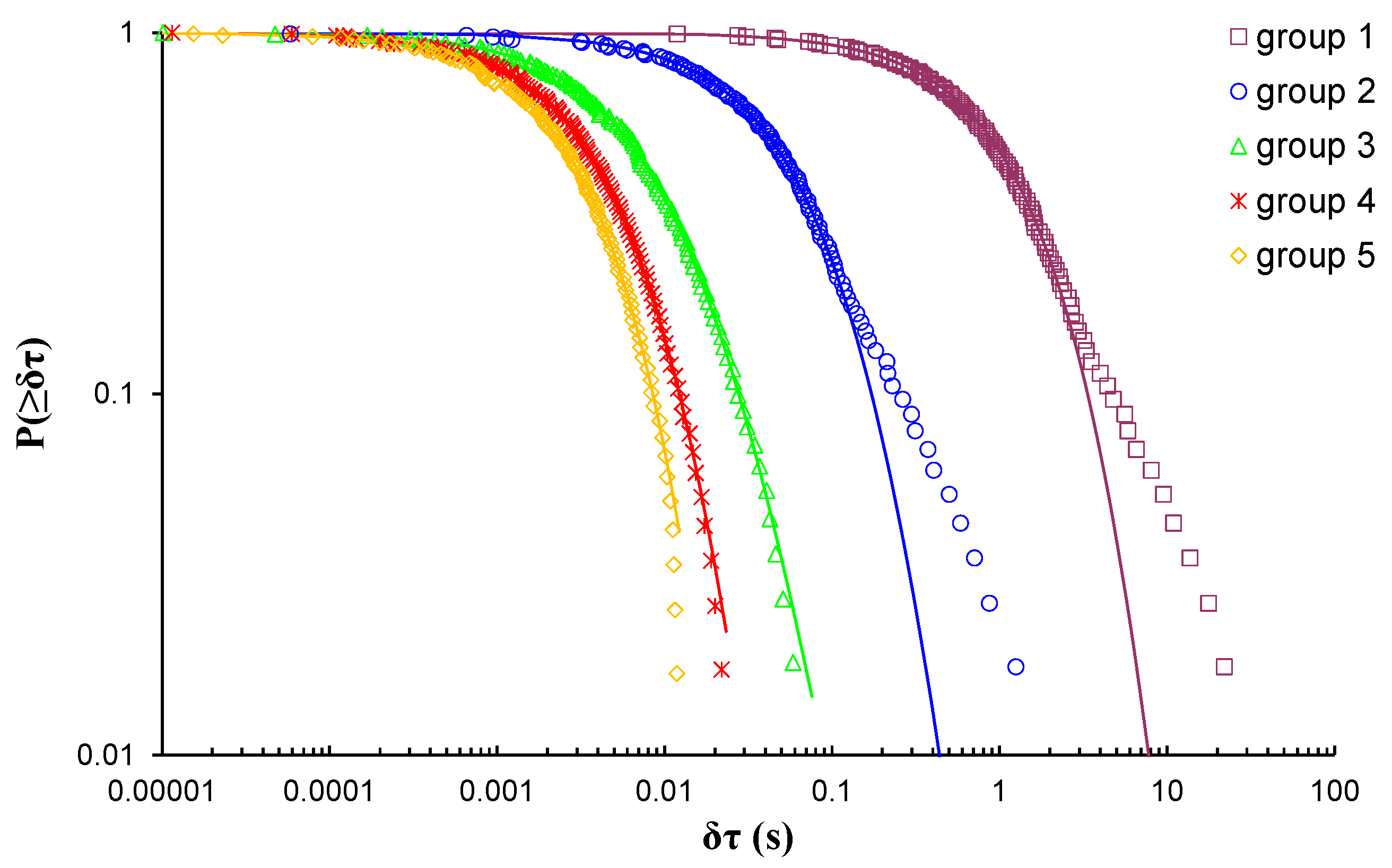
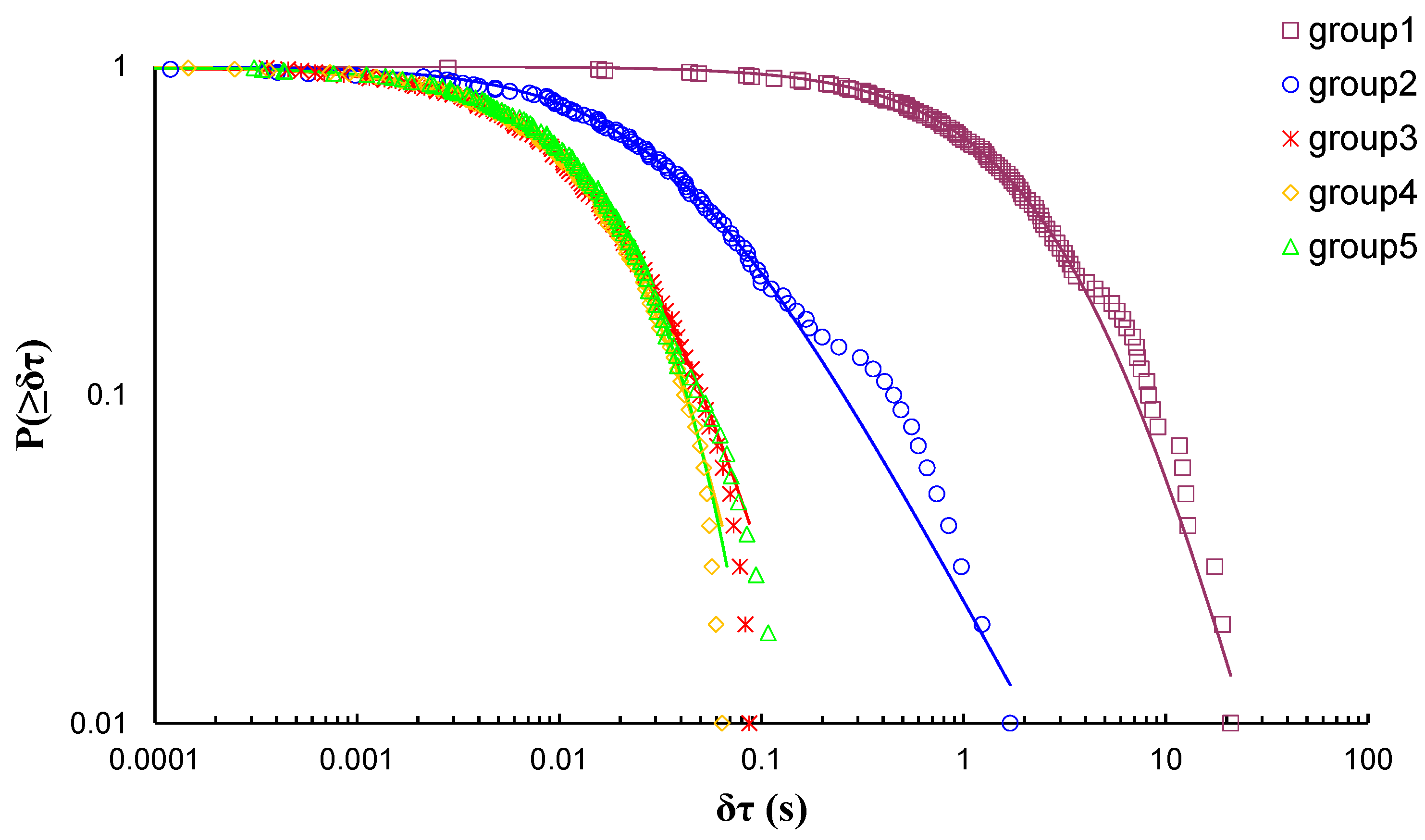
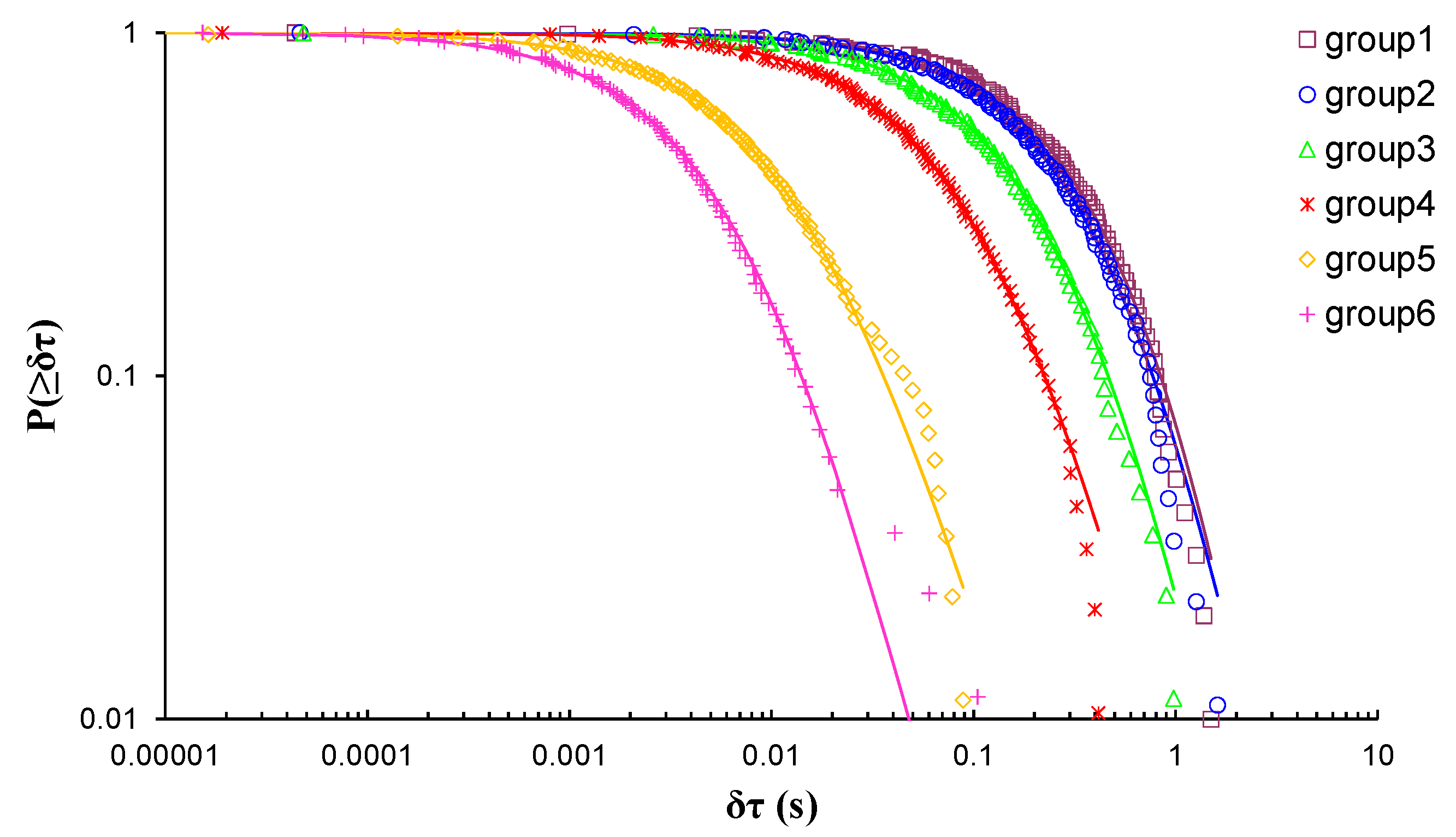
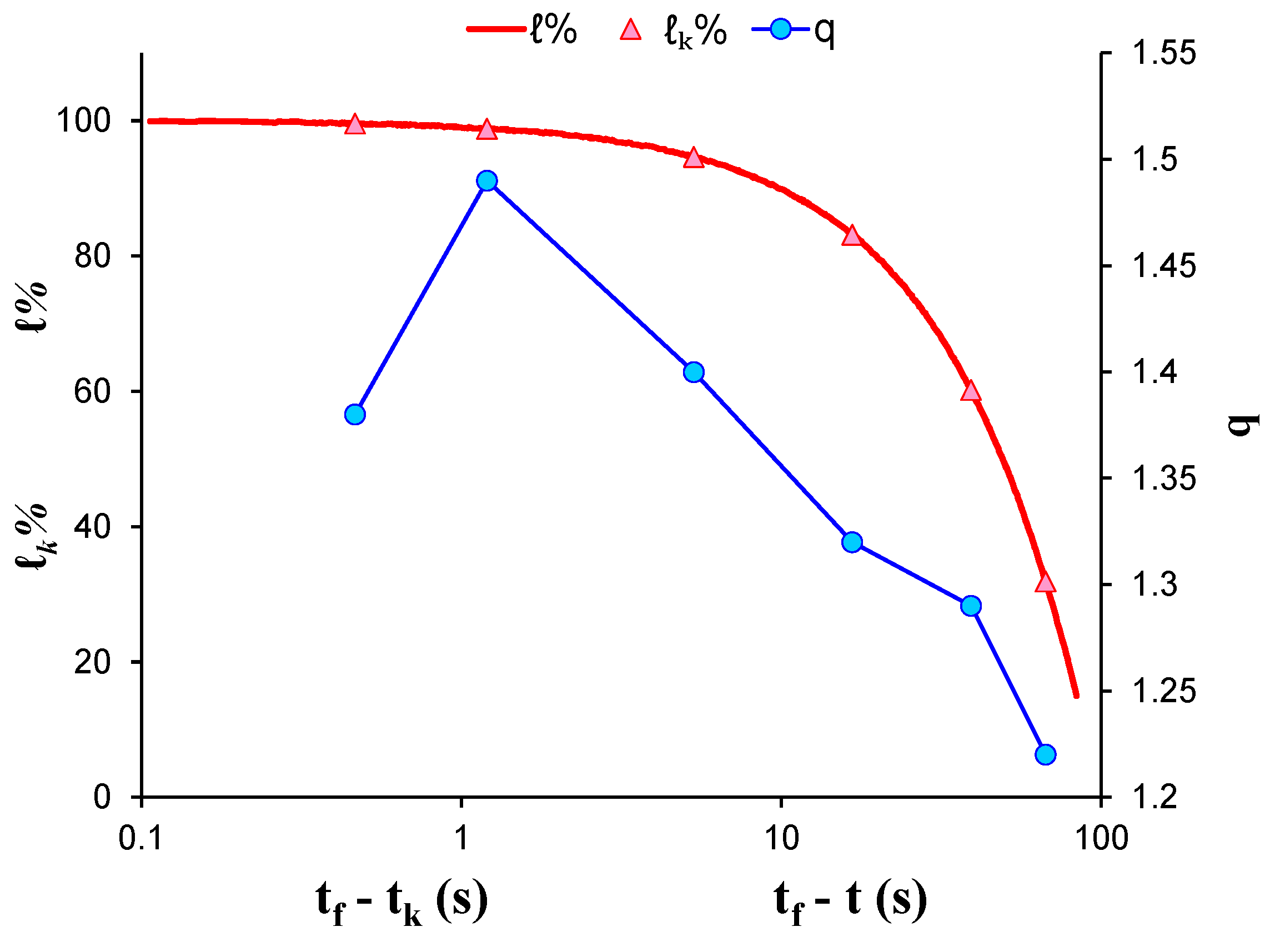
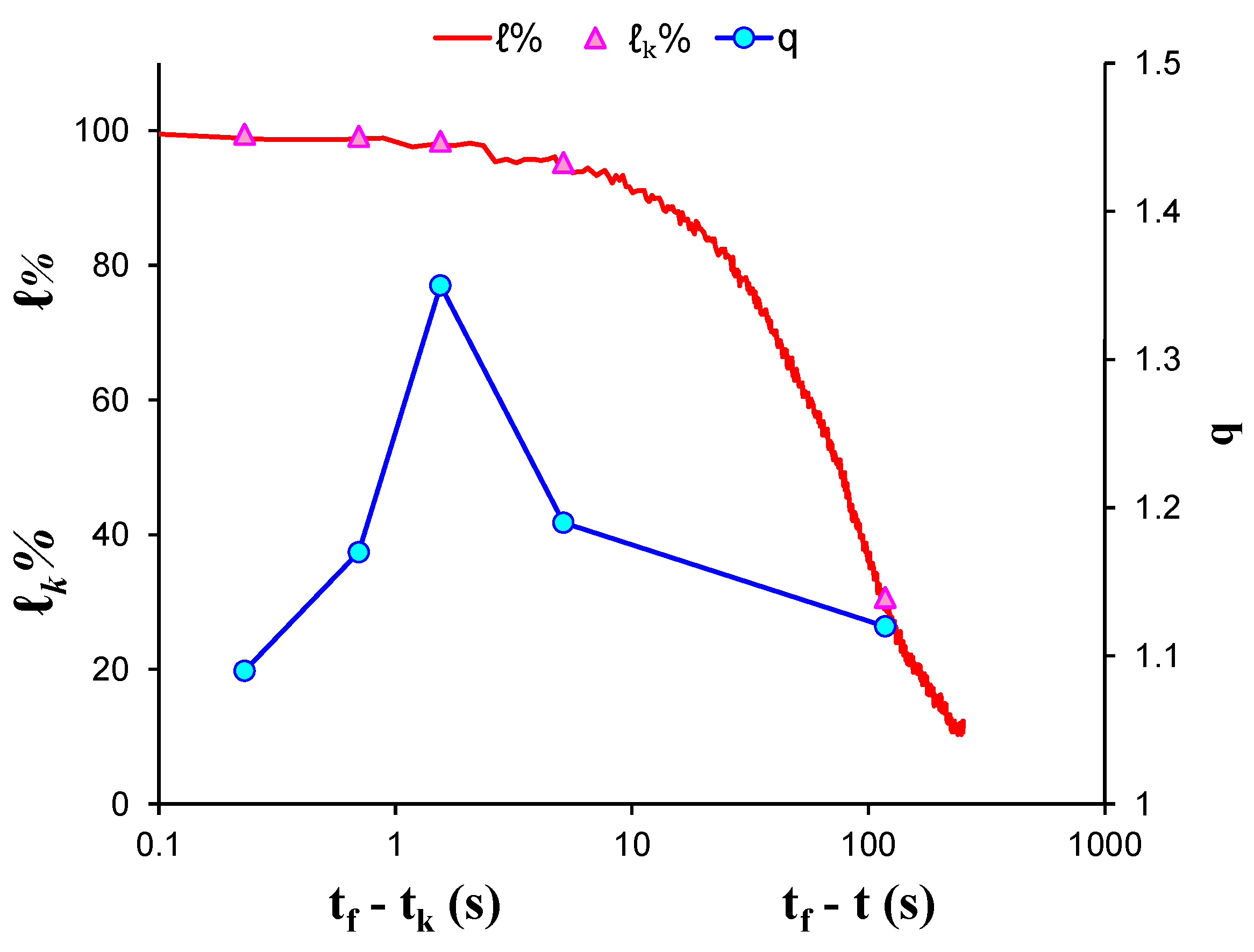
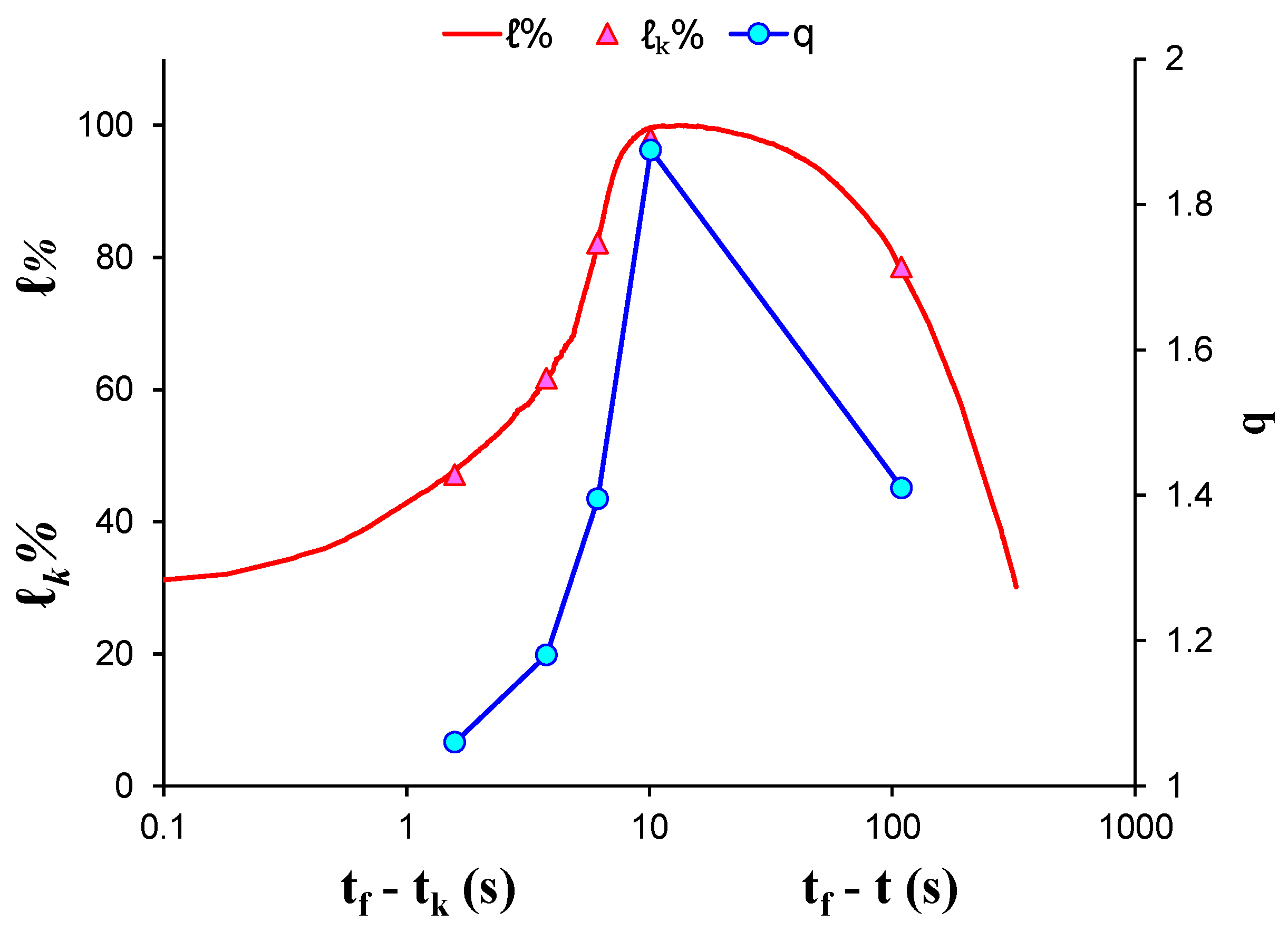
| Experiment | Loading Protocol | Material | Total AE Hits |
|---|---|---|---|
| 1 | Three-point bending | Marble | 790 |
| 2 | Direct tension | “ | 574 |
| 3 | Diametral compression | “ | 507 |
| 4 | Three-point bending | Cement mortar | 549 |
| AE Hit Group | (%) | ||||
|---|---|---|---|---|---|
| 1 | 881.12 | 1.17 | 0.24 | 4.167 | 19.8 |
| 2 | 490.93 | 1.21 | 0.32 | 3.125 | 50.7 |
| 3 | 253.75 | 1.19 | 0.75 | 1.333 | 74.2 |
| 4 | 124.65 | 1.27 | 1.10 | 0.909 | 88.5 |
| 5 | 44.70 | 1.38 | 2.50 | 0.400 | 97.3 |
| 6 | 8.65 | 1.41 | 10.50 | 0.095 | 99.8 |
| 7 | 2.59 | 1.35 | 94.90 | 0.011 | 98.7 |
| 8 | 1.06 | 1.29 | 100.10 | 0.010 | 96.9 |
| AE Hit Group | q | (%) | |||
|---|---|---|---|---|---|
| 1 | 117.8 | 1.12 | 0.79 | 1.2658 | 30.7% |
| 2 | 5.13 | 1.19 | 16.8 | 0.0595 | 95.3% |
| 3 | 1.55 | 1.35 | 127.8 | 0.0078 | 98.4% |
| 4 | 0.70 | 1.17 | 230.2 | 0.0043 | 99.2% |
| 5 | 0.23 | 1.09 | 300.5 | 0.0033 | 99.6% |
| AE Hit Group | q | ||||
|---|---|---|---|---|---|
| 1 | 109.27 | 1.41 | 0.55 | 1.803 | 78.5% |
| 2 | 10.12 | 1.88 | 29.26 | 0.034 | 98.0% |
| 3 | 6.12 | 1.40 | 74.00 | 0.014 | 82.1% |
| 4 | 3.77 | 1.18 | 68.11 | 0.015 | 61.7% |
| 5 | 1.58 | 1.06 | 57.78 | 0.017 | 47.1% |
| AE Hit Group | (s) | q | |||
|---|---|---|---|---|---|
| 1 | 67.07 | 1.22 | 3.56 | 0.2809 | 31.9% |
| 2 | 39.22 | 1.29 | 4.25 | 0.2352 | 60.2% |
| 3 | 16.68 | 1.32 | 7.34 | 0.1362 | 83.2% |
| 4 | 5.33 | 1.40 | 16.86 | 0.0593 | 94.6% |
| 5 | 1.20 | 1.49 | 119.4 | 0.0084 | 98.8% |
| 6 | 0.47 | 1.38 | 262.4 | 0.0038 | 99.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loukidis, A.; Triantis, D.; Stavrakas, I. Non-Extensive Statistical Analysis of Acoustic Emissions: The Variability of Entropic Index q during Loading of Brittle Materials Until Fracture. Entropy 2021, 23, 276. https://doi.org/10.3390/e23030276
Loukidis A, Triantis D, Stavrakas I. Non-Extensive Statistical Analysis of Acoustic Emissions: The Variability of Entropic Index q during Loading of Brittle Materials Until Fracture. Entropy. 2021; 23(3):276. https://doi.org/10.3390/e23030276
Chicago/Turabian StyleLoukidis, Andronikos, Dimos Triantis, and Ilias Stavrakas. 2021. "Non-Extensive Statistical Analysis of Acoustic Emissions: The Variability of Entropic Index q during Loading of Brittle Materials Until Fracture" Entropy 23, no. 3: 276. https://doi.org/10.3390/e23030276
APA StyleLoukidis, A., Triantis, D., & Stavrakas, I. (2021). Non-Extensive Statistical Analysis of Acoustic Emissions: The Variability of Entropic Index q during Loading of Brittle Materials Until Fracture. Entropy, 23(3), 276. https://doi.org/10.3390/e23030276







