A New Algorithm for Digital Image Encryption Based on Chaos Theory
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chaos and Transformation Theories
2.2. Chaotic Sequence Based on Logistic Map
- Step NO.1:
- In the first step, two chaotic sequences, x = {x1, x2… xm×n} are produced by two one-dimensional logistic maps. Place the two logistic maps system parameter as a primary value as x1(0) and x2(0), respectively.
- Step NO.2:
- In the second step, for every iteration, compare x1(i), and x2(i), i = 1, 2, m × n and choose one that is numerically larger.
- Step NO.3:
- In the next step, perform the Exclusive NOR (XNOR) operation for sequences produced by Step NO.2 with the original image’s pixels.
- Step NO.4:
- In the last step, change the encrypted one-dimensional matrix, namely P, into a two-dimensional matrix. Set the size of this modified matrix to m × n. In this process, a two-dimensional data matrix R2 is generated. Thus, a diffused image is obtained.
2.3. Kinetics of Coupled Map Lattice
- Step NO.1:
- In the first step, the chaotic sequences x1, x2 = {x1, x2… xm} are produced with the length of m, and y1, y2 = {y1, y2… yn} with the length of n similar to CML chaos mapping.
- Step NO.2:
- In the second step, x, y chaotic sequences are arranged in rising sequences, producing position sequences w2, w3.
- Step NO.3:
- In the last step, the pixel confusion is performed, using w2, w3 as the row, and column sequences of the data matrix R.
2.4. Wavelet Transform
3. Proposed Algorithm
- Step NO.1:
- In the first step, a grayscale image G is arranged. The image’s size is set to m × n. Moreover, data matrix R is placed. By evaluating two logistic maps, a chaotic sequence is generated. Making XNOR with the primary image, the diffusion is terminated.
- Step NO.2:
- In this step, for the diffused image in step NO.1, the wavelet decomposition is performed and then the wavelet coefficient is extracted, registered as ca1.
- Step NO.3:
- Utilizing a two-dimensional hyper-chaotic map CML, the chaotic sequence is produced, and with ca1 established in step NO.2, the position confusion is performed.
- Step NO.4:
- In the last step, the confused image can be rebuilt by wavelet. After all, the encrypted image is obtained. The inverse operations of the encryption are known as the decryption algorithm. System parameters and the primary value of the chaotic sequences in the image encryption and image decryption are consistent.
3.1. Encryption Assessments Metrics
3.2. Peak Signal to Noise Ratio (PSNR)
3.3. Number of Pixels Change Rate (NPCR)
3.4. Unified Average Changing Intensity (UACI)
3.5. Correlation Coefficient
4. Experimental and Numerical Results
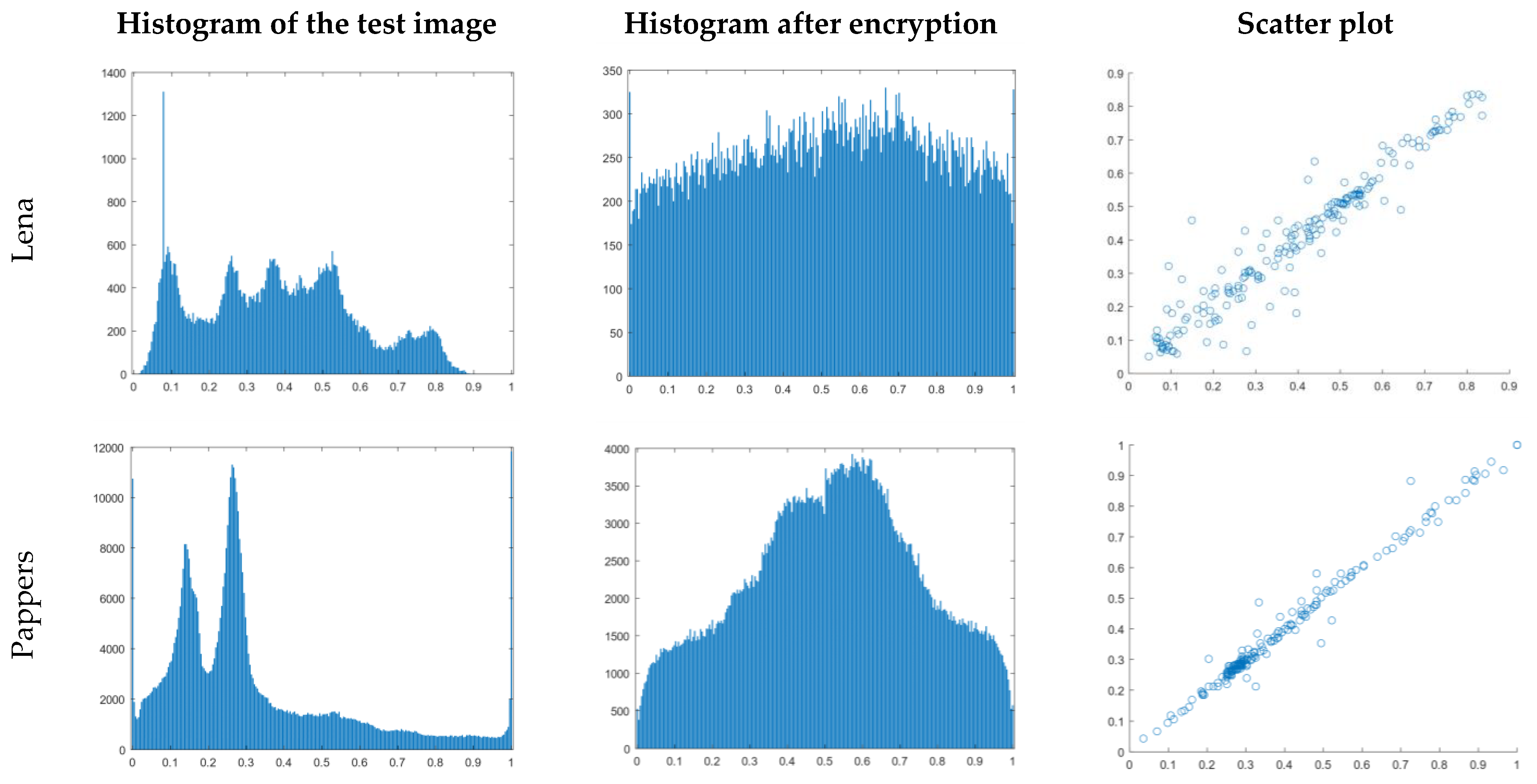
4.1. Histogram Analysis
4.2. Complexity
4.3. Robustness
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hamzenejad, A.; Ghoushchi, S.J.; Baradaran, V.; Mardani, A. A Robust Algorithm for Classification and Diagnosis of Brain Disease Using Local Linear Approximation and Generalized Autoregressive Conditional Heteroscedasticity Model. Mathematics 2020, 8, 1268. [Google Scholar] [CrossRef]
- Filelis-Papadopoulos, C.K.; Endo, P.T.; Bendechache, M.; Svorobej, S.; Giannoutakis, K.M.; Gravvanis, G.A.; Tzovaras, D.; Byrne, J.; Lynn, T. Towards simulation and optimization of cache placement on large virtual content distribution networks. J. Comput. Sci. 2020, 39, 101052. [Google Scholar] [CrossRef]
- Bendechache, M.; Kechadi, M.T. Distributed clustering algorithm for spatial data mining. In Proceedings of the 2015 2nd IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services (ICSDM), Fuzhou, China, 8–10 July 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 60–65. [Google Scholar] [CrossRef] [Green Version]
- Bendechache, M.; Svorobej, S.; Endo, P.T.; Lynn, T. Simulating Resource Management across the Cloud-to-Thing Continuum: A Survey and Future Directions. Future Internet 2020, 12, 95. [Google Scholar] [CrossRef]
- Saračević, M.H.; Adamović, S.Z.; Miškovic, V.A.; Elhoseny, M.; Maček, N.D.; Selim, M.M.; Shankar, K. Data Encryption for Internet of Things Applications Based on Catalan Objects and Two Combinatorial Structures; IEEE Transactions on Reliability: Piscataway, NJ, USA, 2020. [Google Scholar]
- Saračević, M.; Adamović, S.; Miškovic, V.; Maček, N.; Šarac, M. A novel approach to steganography based on the properties of Catalan numbers and Dyck words. Future Gener. Comput. Syst. 2019, 100, 186–197. [Google Scholar] [CrossRef]
- Jafarzadeh, S.G.; Rahman, M.N.A.; Wahab, D.A. Optimization of supply chain management based on response surface methodology: A case study of iran khodro. World Appl. Sci. J. 2012, 20, 620–627. [Google Scholar]
- Jafarzadeh-Ghoushchi, S. Qualitative and quantitative analysis of Green Supply Chain Management (GSCM) literature from 2000 to 2015. Int. J. Supply Chain Manag. 2018, 7, 77–86. [Google Scholar]
- Jafarzadeh Ghoushchi, S.; Khazaeili, M.; Amini, A.; Osgooei, E. Multi-criteria sustainable supplier selection using piecewise linear value function and fuzzy best-worst method. J. Intell. Fuzzy Syst. 2019, 37, 2309–2325. [Google Scholar] [CrossRef]
- Dorosti, S.; Ghoushchi, S.J.; Sobhrakhshankhah, E.; Ahmadi, M.; Sharifi, A. Application of gene expression programming and sensitivity analyses in analyzing effective parameters in gastric cancer tumor size and location. Soft Comput. 2020, 24, 9943–9964. [Google Scholar] [CrossRef]
- Ramalingam, B.; Ravichandran, D.; Annadurai, A.A.; Rengarajan, A.; Rayappan, J.B.B. Chaos triggered image encryption—A reconfigurable security solution. Multimed. Tools Appl. 2017, 77, 11669–11692. [Google Scholar] [CrossRef]
- Svorobej, S.; Endo, P.T.; Bendechache, M.; Filelis-Papadopoulos, C.; Giannoutakis, K.M.; Gravvanis, G.A.; Tzovaras, D.; Byrne, J.; Lynn, T. Simulating Fog and Edge Computing Scenarios: An Overview and Research Challenges. Future Internet 2019, 11, 55. [Google Scholar] [CrossRef] [Green Version]
- Bendechache, M.; Kechadi, M.-T.; Le-Khac, N.-A. Efficient Large Scale Clustering Based on Data Partitioning. In Proceedings of the 2016 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Montreal, QC, Canada, 17–19 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 612–621. [Google Scholar]
- Khan, J.S.; Ahmad, J. Chaos based efficient selective image encryption. Multidimens. Syst. Signal Process. 2019, 30, 943–961. [Google Scholar] [CrossRef]
- Wang, Y.; Wong, K.-W.; Liao, X.; Chen, G. A new chaos-based fast image encryption algorithm. Appl. Soft Comput. 2011, 11, 514–522. [Google Scholar] [CrossRef]
- Patidar, V.; Pareek, N.; Purohit, G.; Sud, K. A robust and secure chaotic standard map based pseudorandom permutation-substitution scheme for image encryption. Opt. Commun. 2011, 284, 4331–4339. [Google Scholar] [CrossRef]
- Wang, X.; Liu, L.; Zhang, Y. A novel chaotic block image encryption algorithm based on dynamic random growth technique. Opt. Lasers Eng. 2015, 66, 10–18. [Google Scholar] [CrossRef]
- Volos, C.; Kyprianidis, I.; Stouboulos, I. Image encryption process based on chaotic synchronization phenomena. Signal Process. 2013, 93, 1328–1340. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, H.; Li, Y.; Pei, B. Image encryption based on synchronization of fractional chaotic systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3735–3744. [Google Scholar] [CrossRef]
- Enayatifar, R.; Abdullah, A.H.; Isnin, I.F. Chaos-based image encryption using a hybrid genetic algorithm and a DNA sequence. Opt. Lasers Eng. 2014, 56, 83–93. [Google Scholar] [CrossRef]
- Xu, L.; Li, Z.; Li, J.; Hua, W. A novel bit-level image encryption algorithm based on chaotic maps. Opt. Lasers Eng. 2016, 78, 17–25. [Google Scholar] [CrossRef]
- Kaur, M.; Kumar, V. Beta Chaotic Map Based Image Encryption Using Genetic Algorithm. Int. J. Bifurc. Chaos 2018, 28. [Google Scholar] [CrossRef]
- Nematzadeh, H.; Enayatifar, R.; Motameni, H.; Guimarães, F.G.; Coelho, V.N. Medical image encryption using a hybrid model of modified genetic algorithm and coupled map lattices. Opt. Lasers Eng. 2018, 110, 24–32. [Google Scholar] [CrossRef]
- Javidi, M.; Hosseinpourfard, R. Chaos Genetic Algorithm Instead Genetic Algorithm. Int. Arab J. Inf. Technol. 2015, 12, 2. [Google Scholar]
- Zhen, P.; Zhao, G.; Min, L.; Jin, X. Chaos-based image encryption scheme combining DNA coding and entropy. Multimed. Tools Appl. 2016, 75, 6303–6319. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, H.-L. A novel image encryption algorithm based on genetic recombination and hyper-chaotic systems. Nonlinear Dyn. 2016, 83, 333–346. [Google Scholar] [CrossRef]
- Li, C.-L.; Li, H.-M.; Li, F.-D.; Wei, D.-Q.; Yang, X.-B.; Zhang, J. Multiple-image encryption by using robust chaotic map in wavelet transform domain. Optik 2018, 171, 277–286. [Google Scholar] [CrossRef]
- Satish, T.J.; Theja, M.N.S.; Kumar, G.G.; Thanikaiselvan, V. Image Encryption Using Integer Wavelet Transform, Logistic Map and XOR Encryption. In Proceedings of the 2018 Second International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 29–31 March 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 704–709. [Google Scholar]
- Kanso, A.; Ghebleh, M. An algorithm for encryption of secret images into meaningful images. Opt. Lasers Eng. 2017, 90, 196–208. [Google Scholar] [CrossRef]
- Ravichandran, D.; Murthy, B.K.; Balasubramanian, V.; Fathima, S.; Amirtharajan, R. An efficient medical image encryption using hybrid DNA computing and chaos in transform domain. Med. Biol. Eng. Comput. 2021, 59, 589–605. [Google Scholar] [CrossRef] [PubMed]
- Kovalchuk, A.; Izonin, I.; Kustra, N. Information Protection Service using Topological Image Coverage. Procedia Comput. Sci. 2019, 160, 503–508. [Google Scholar] [CrossRef]
- Kovalchuk, A.; Lotoshynska, N.; Izonin, I.; Berezko, L. An Approach towards an Efficient Encryption-Decryption of Grayscale and Color Images. Procedia Comput. Sci. 2019, 155, 630–635. [Google Scholar] [CrossRef]
- Kovalchuk, A.; Izonin, I.; Lotoshynska, N. An Approach Towards Image Encryption and Decryption using Quaternary Fractional-Linear Operations. Procedia Comput. Sci. 2019, 160, 491–496. [Google Scholar] [CrossRef]
- Kovalchuk, A.; Izonin, I.; Strauss, C.; Podavalkina, M.; Lotoshynska, N.; Kustra, N. Image Encryption and Decryption Schemes Using Linear and Quadratic Fractal Algorithms and Their Systems. In DCSMart; Researchgate: Berlin, Germany, 2019; pp. 139–150. [Google Scholar]
- Kovalchuk, A.; Izonin, I.; Riznyk, O. An Efficient Image Encryption Scheme using Projective Transformations. Procedia Comput. Sci. 2019, 160, 584–589. [Google Scholar] [CrossRef]
- Kovalchuk, A.; Lotoshynska, N. Elements of RSA Algorithm and Extra Noising in a Binary Linear-Quadratic Transformations During Encryption and Decryption of Images. In Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 21–25 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 542–544. [Google Scholar]
- Hafsa, A.; Gafsi, M.; Malek, J.; Machhout, M. FPGA Implementation of Improved Security Approach for Medical Image Encryption and Decryption. Sci. Program. 2021, 2021, 6610655. [Google Scholar]
- Kari, A.P.; Navin, A.H.; Bidgoli, A.M.; Mirnia, M. A new image encryption scheme based on hybrid chaotic maps. Multimed. Tools Appl. 2021, 80, 2753–2772. [Google Scholar] [CrossRef]
- Shaukat, S.; Arshid, A.L.; Eleyan, A.; Shah, S.A.; Ahmad, J. Chaos theory and its application: An essential framework for image encryption. Chaos Theory Appl. 2020, 2, 17–22. [Google Scholar]
- Guo, J. Basic theories and applications of digital image processing. In Proceedings of the 2017 2nd International Conference on Mechatronics and Information Technology, Dalian, China, 13–14 May 2017; Francis Academic Press Ltd.: London, UK, 2017. [Google Scholar]
- Bendechache, M. Study of Distributed Dynamic Clustering Framework for Spatial Data Mining. Available online: http://oatd.org/oatd/record?record=handle%5C%3A10197%5C%2F10614 (accessed on 17 December 2020).
- Gad, M.; Hagras, E.; Soliman, H.; Hikal, N. A New Parallel Fuzzy Multi Modular Chaotic Logistic Map for Image Encryption. Int. Arab J. Inf. Technol. 2021, 18, 227–236. [Google Scholar]
- Yang, J.; Gao, J.S.; Sun, B.Y. An improved approach of logistic chaotic series encryption. Tech. Autom. Appl. 2004, 23, 58–61. [Google Scholar]
- Hao, Z.; Xing-Yuan, W.; Si-Wei, W.; Kang, G.; Xiao-Hui, L. Application of coupled map lattice with parameter q in image encryption. Opt. Lasers Eng. 2017, 88, 65–74. [Google Scholar] [CrossRef]
- Pisarchik, A.; Zanin, M. Image encryption with chaotically coupled chaotic maps. Phys. D Nonlinear Phenom. 2008, 237, 2638–2648. [Google Scholar] [CrossRef]
- Lu, G.; Smidtaite, R.; Navickas, Z.; Ragulskis, M. The Effect of Explosive Divergence in a Coupled Map Lattice of Matrices. Chaos Solitons Fractals 2018, 113, 308–313. [Google Scholar] [CrossRef]
- Rai, H.M.; Chatterjee, K. Hybrid adaptive algorithm based on wavelet transform and independent component analysis for denoising of MRI images. Measurement 2019, 144, 72–82. [Google Scholar] [CrossRef]
- Eftekhari, H.R.; Ghatee, M. Hybrid of discrete wavelet transform and adaptive neuro fuzzy inference system for overall driving behavior recognition. Transp. Res. Part F Traffic Psychol. Behav. 2018, 58, 782–796. [Google Scholar] [CrossRef]
- Wu, F.; Hao, Y.; Zhao, J.; Liu, Y. Current similarity based open-circuit fault diagnosis for induction motor drives with discrete wavelet transform. Microelectron. Reliab. 2017, 75, 309–316. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Saadi, S.B. Automated liver and tumor segmentation based on concave and convex points using fuzzy c-means and mean shift clustering. Measurement 2020, 150, 107086. [Google Scholar] [CrossRef]
- Mokhtari, Z.; Melkemi, K. A New Watermarking Algorithm Based on Entropy Concept. Acta Appl. Math. 2011, 116, 65–69. [Google Scholar] [CrossRef]
- Ali, W.A.; Aljunid, M.; Bendechache, M.; Sandhya, P. Review of Current Machine Learning Approaches for Anomaly Detection in Network Traffic. J. Telecommun. Digit. Econ. 2020, 8, 64–95. [Google Scholar] [CrossRef]
- Karimi, N.; Kondrood, R.R.; Alizadeh, T. An intelligent system for quality measurement of Golden Bleached raisins using two comparative machine learning algorithms. Measurement 2017, 107, 68–76. [Google Scholar] [CrossRef]
- Yan, X.; Wang, S.; Li, L.; El-Latif, A.A.A.; Wei, Z.; Niu, X. A New Assessment Measure of Shadow Image Quality Based on Error Diffusion Techniques. J. Inf. Hiding Multimed. Signal Process. 2013, 4, 118–126. [Google Scholar]
- Fu, C.; Chen, J.-J.; Zou, H.; Meng, W.-H.; Zhan, Y.-F.; Yu, Y.-W. A chaos-based digital image encryption scheme with an improved diffusion strategy. Opt. Express 2012, 20, 2363–2378. [Google Scholar] [CrossRef]
- Mera, C.; Orozco-Alzate, M.; Branch, J.; Mery, D. Automatic visual inspection: An approach with multi-instance learning. Comput. Ind. 2016, 83, 46–54. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Saadi, S.B.; Amirabadi, A. LNPSS: SAR image despeckling based on local and non-local features using patch shape selection and edges linking. Measurement 2020, 164, 107989. [Google Scholar] [CrossRef]
- Ahmadi, M.; Jafarzadeh-Ghoushchi, S.; Taghizadeh, R.; Sharifi, A. Presentation of a new hybrid approach for forecasting economic growth using artificial intelligence approaches. Neural Comput. Appl. 2019, 31, 8661–8680. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Chen, C.-H.; Lin, K.-P. An automatic filtering convergence method for iterative impulse noise filters based on PSNR checking and filtered pixels detection. Expert Syst. Appl. 2016, 63, 198–207. [Google Scholar] [CrossRef]
- Orozco, E.R.; Guerrero, E.E.G.; González, E.I.; Bonilla, O.R.L. Image Encryption Based on Improved Rosslerö Hyper chaotic Map. 2015. Available online: https://pdfs.semanticscholar.org/8e23/a3dc5c12d5d52c8f76084906ac68cc7b40b5.pdf (accessed on 30 March 2015).
- Zhou, N.; Wang, Y.; Gong, L.; He, H.; Wu, J. Novel single-channel color image encryption algorithm based on chaos and fractional Fourier transform. Opt. Commun. 2011, 284, 2789–2796. [Google Scholar] [CrossRef]
- Salem, S.; Jafarzadeh-Ghoushchi, S. Estimation of optimal physico-chemical characteristics of nano-sized inorganic blue pigment by combined artificial neural network and response surface methodology. Chemom. Intell. Lab. Syst. 2016, 159, 80–88. [Google Scholar] [CrossRef]
- Ranjbarzadeh, R.; Baseri Saadi, S. Corrigendum to ‘Automated liver and tumor segmentation based on concave and convex points using fuzzy c-means and mean shift clustering’ [Measurement 150 (2020) 107086]. Meas. J. Int. Meas. Confed. 2020, 151, 107230. [Google Scholar] [CrossRef]
- Blaber, J.; Adair, B.S.; Antoniou, A. Ncorr: Open-Source 2D Digital Image Correlation Matlab Software. Exp. Mech. 2015, 55, 1105–1122. [Google Scholar] [CrossRef]
- Niu, Y.; Zhang, X.; Han, F. Image Encryption Algorithm Based on Hyperchaotic Maps and Nucleotide Sequences Database. Comput. Intell. Neurosci. 2017, 2017, 1–9. [Google Scholar] [CrossRef] [Green Version]
- May, R.M. Simple mathematical models with very complicated dynamics. In The Theory of Chaotic Attractors; Springer: New York, NY, USA, 2004; pp. 85–93. [Google Scholar]
- Solak, E.; Çokal, C.; Yildiz, O.T.; Biyikoğlu, T. Cryptanalysis of fridrich’s chaotic image encryption. Int. J. Bifurc. Chaos 2010, 20, 1405–1413. [Google Scholar] [CrossRef] [Green Version]
- Rhouma, R.; Solak, E.; Belghith, S. Cryptanalysis of a new substitution–diffusion based image cipher. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1887–1892. [Google Scholar] [CrossRef]
- Amina, S.; Mohamed, F.K. An efficient and secure chaotic cipher algorithm for image content preservation. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 12–32. [Google Scholar] [CrossRef]
- Yavuz, E.; Yazıcı, R.; Kasapbaşı, M.C.; Yamaç, E. A chaos-based image encryption algorithm with simple logical functions. Comput. Electr. Eng. 2016, 54, 471–483. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, Z. Chaos-based image encryption with total shuffling and bidirectional diffusion. Nonlinear Dyn. 2013, 75, 319–330. [Google Scholar] [CrossRef]
- El Assad, S.; Farajallah, M. A new chaos-based image encryption system. Signal Process. Image Commun. 2016, 41, 144–157. [Google Scholar] [CrossRef]






| Image | Type of Image | PSNR | NPCR | UACI | NC |
|---|---|---|---|---|---|
| Lena Image | Jpg | 42.612 | 99.757 | 33.120 | 0.9548 |
| Peppers Image | Jpg | 39.220 | 99.787 | 33.621 | 0.9934 |
| Barbara Image | Jpg | 36.841 | 99.626 | 33.126 | 0.9809 |
| Baboon Image | Jpg | 39.134 | 99.881 | 33.415 | 0.9137 |
| Boat Image | Jpg | 38.223 | 99.625 | 33.671 | 0.9001 |
| x1(1) | x2(1) | µ 1 | µ 2 |
| 0.5 | 0.5 | 4 | 3.9 |
| x3(1) | y3(1) | µ 1 | µ 2 |
| 0.3 | 0.3 | 4 | 3.9 |
| Image | Median Filter | Histogram Equalization | Rotation | Gaussian Noise |
|---|---|---|---|---|
| Lena Image | 0.984 | 0.987 | 0.999 | 0.999 |
| Peppers Image | 0.704 | 0.280 | 0.923 | 0.964 |
| Barbara Image | 0.914 | 0.497 | 0.980 | 0.991 |
| Baboon Image | 0.960 | 0.629 | 0.991 | 0.996 |
| Boat Image | 0.976 | 0.746 | 0.995 | 0.998 |
| Reference | Image | NPCR | UACI |
|---|---|---|---|
| Presented model | Lena Image | 99.757 | 33.120 |
| Presented model | Peppers Image | 99.787 | 33.621 |
| Presented model | Barbara Image | 99.626 | 33.126 |
| Presented model | Baboon Image | 99.881 | 33.415 |
| Presented model | Boat Image | 99.625 | 33.671 |
| Amina et al. [69] | Lena Image | 99.646 | 33.625 |
| Amina et al. [69] | Peppers Image | 99.632 | 33.507 |
| Amina et al. [69] | Baboon Image | 99.602 | 33.629 |
| Yavuz et al. [70] | Lena Image | 99.620 | 33.410 |
| Zhang and Zhao [71] | Lena Image | 99.605 | 33.411 |
| Assad and Farajallah [72] | Lena Image | 99.607 | 33.463 |
| Assad and Farajallah [72] | Boat Image | 99.615 | 33.465 |
| Kari et al. [38] | Lena Image | 99.646 | 33.625 |
| Kari et al. [38] | Peppers Image | 99.713 | 33.541 |
| Kari et al. [38] | Baboon Image | 99.623 | 33.416 |
| Kari et al. [38] | Boat Image | 99.619 | 33.556 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pourasad, Y.; Ranjbarzadeh, R.; Mardani, A. A New Algorithm for Digital Image Encryption Based on Chaos Theory. Entropy 2021, 23, 341. https://doi.org/10.3390/e23030341
Pourasad Y, Ranjbarzadeh R, Mardani A. A New Algorithm for Digital Image Encryption Based on Chaos Theory. Entropy. 2021; 23(3):341. https://doi.org/10.3390/e23030341
Chicago/Turabian StylePourasad, Yaghoub, Ramin Ranjbarzadeh, and Abbas Mardani. 2021. "A New Algorithm for Digital Image Encryption Based on Chaos Theory" Entropy 23, no. 3: 341. https://doi.org/10.3390/e23030341
APA StylePourasad, Y., Ranjbarzadeh, R., & Mardani, A. (2021). A New Algorithm for Digital Image Encryption Based on Chaos Theory. Entropy, 23(3), 341. https://doi.org/10.3390/e23030341







