Interstage Pressures of a Multistage Compressor with Intercooling
Abstract
:1. Introduction
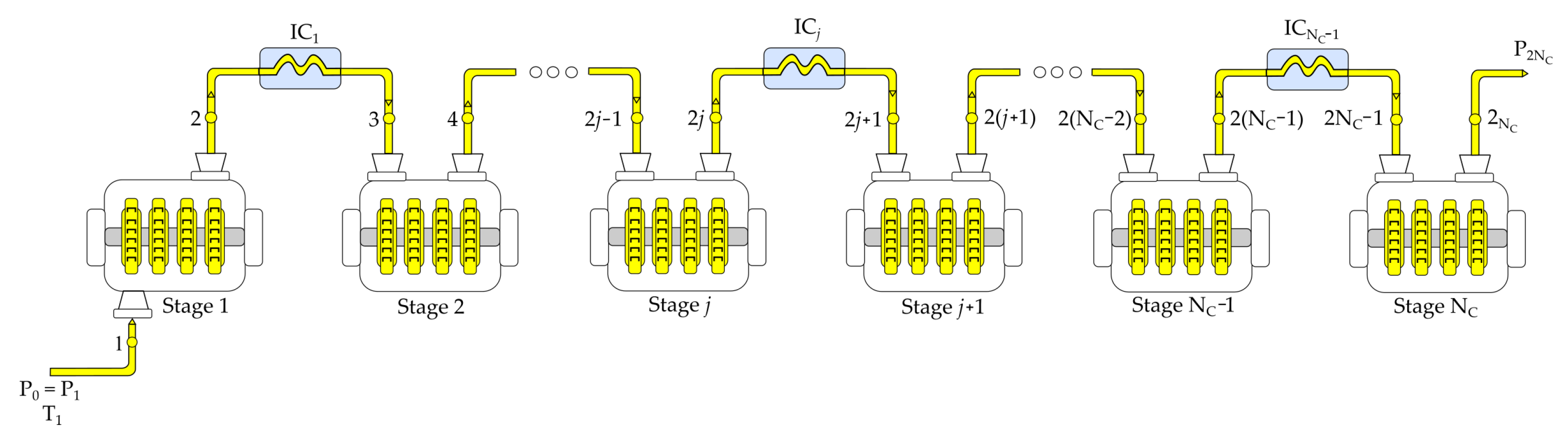
2. System Description and Assumptions
- A constant mass flow rate of a working fluid behaving as an ideal gas with constant heat capacities is compressed.
- The gas undergoes a pressure drop in each j-intercooler—see Figure 2. The pressure drop coefficient across the j-intercooler is defined aswhere and denote the inlet and outlet pressures for the j intercooling process, and they also correspond to the discharge pressure of the j compressor and the suction pressure of the compressor stage, respectively. In this way, Equation (1) for allows us to obtain the following expression for the suction pressure of the j compression stage, , in terms of the pressure drop coefficient of the intercooler and the outlet pressure of the compression stage,The above equation is valid if we define and therefore .
- The gas temperature at the inlet of each compressor is not assumed to be the same. However, the compressed gas outlet temperature of each intercooler is close to .
- The isentropic efficiencies of the individual compressors are assumed to be different, and the compression from to is considered to occur at constant isentropic efficiency,where and are the isentropic and actual adiabatic specific works provided to the j compression stage, respectively. The ideal compression work conducted on the j compression process corresponds to the work conducted on an isentropic compression process beginning at the same initial state and proceeding to the same final pressure (but not the same final state) as the actual compression process.
3. Theoretical Model
3.1. Optimal Interstage Pressures for Minimum Compression Specific Work
3.2. Minimum Compression Specific Work
4. Applications
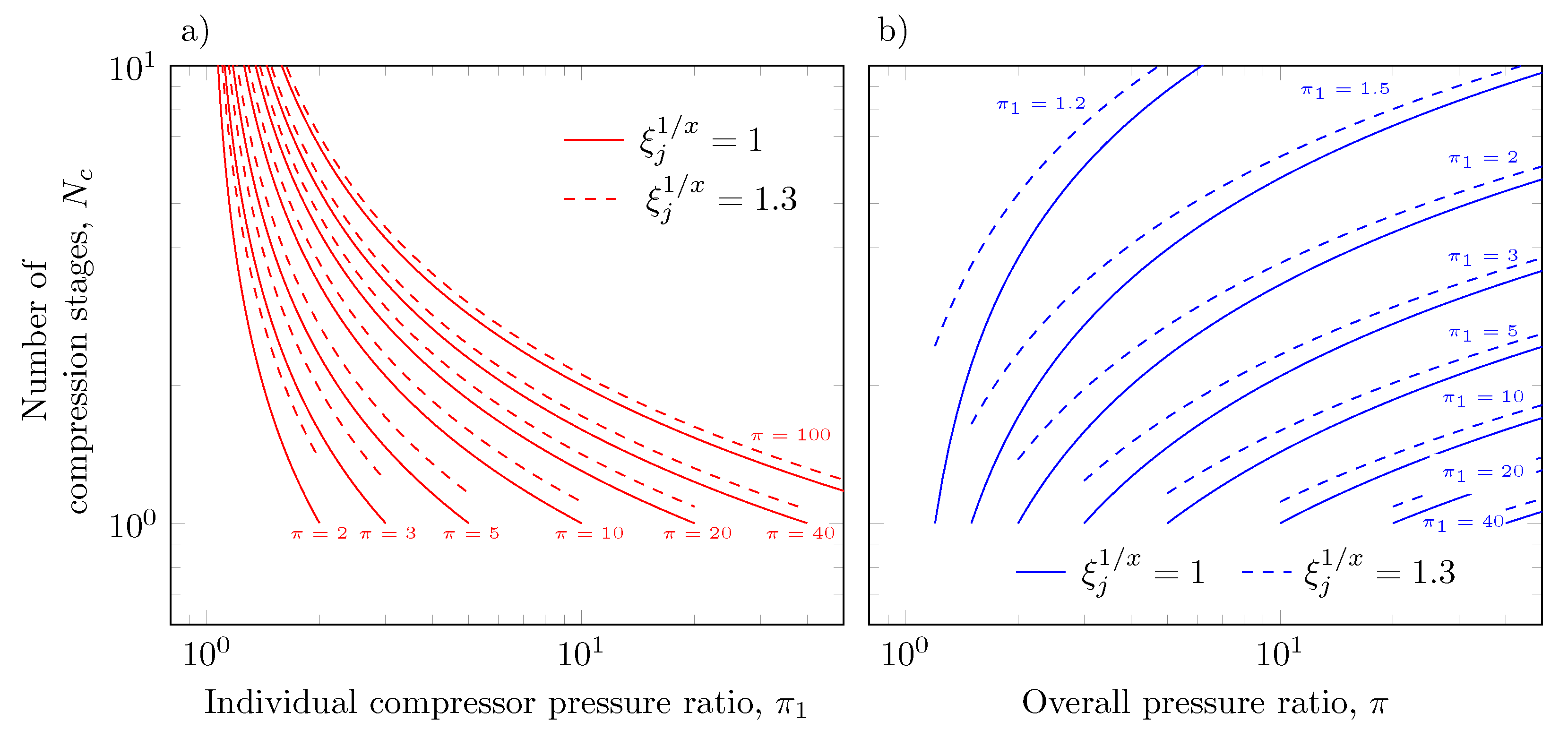
4.1. Estimation of the Number of Compression Stages
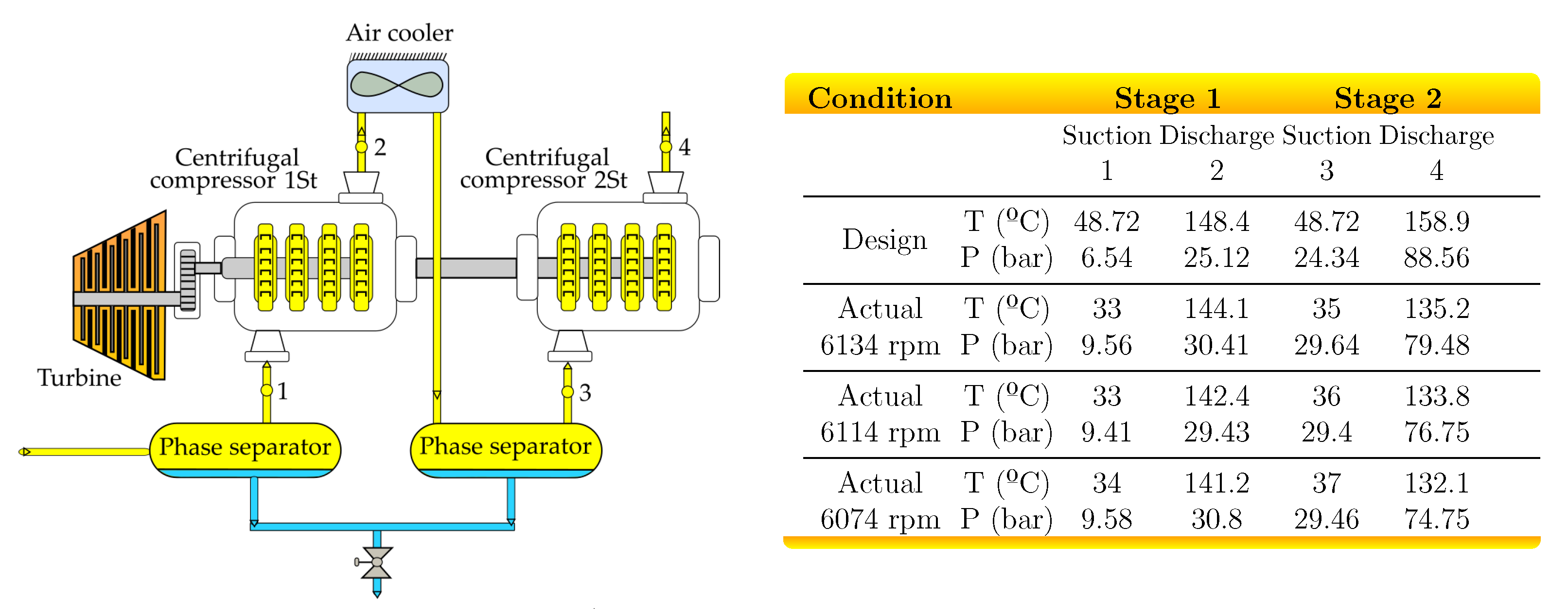
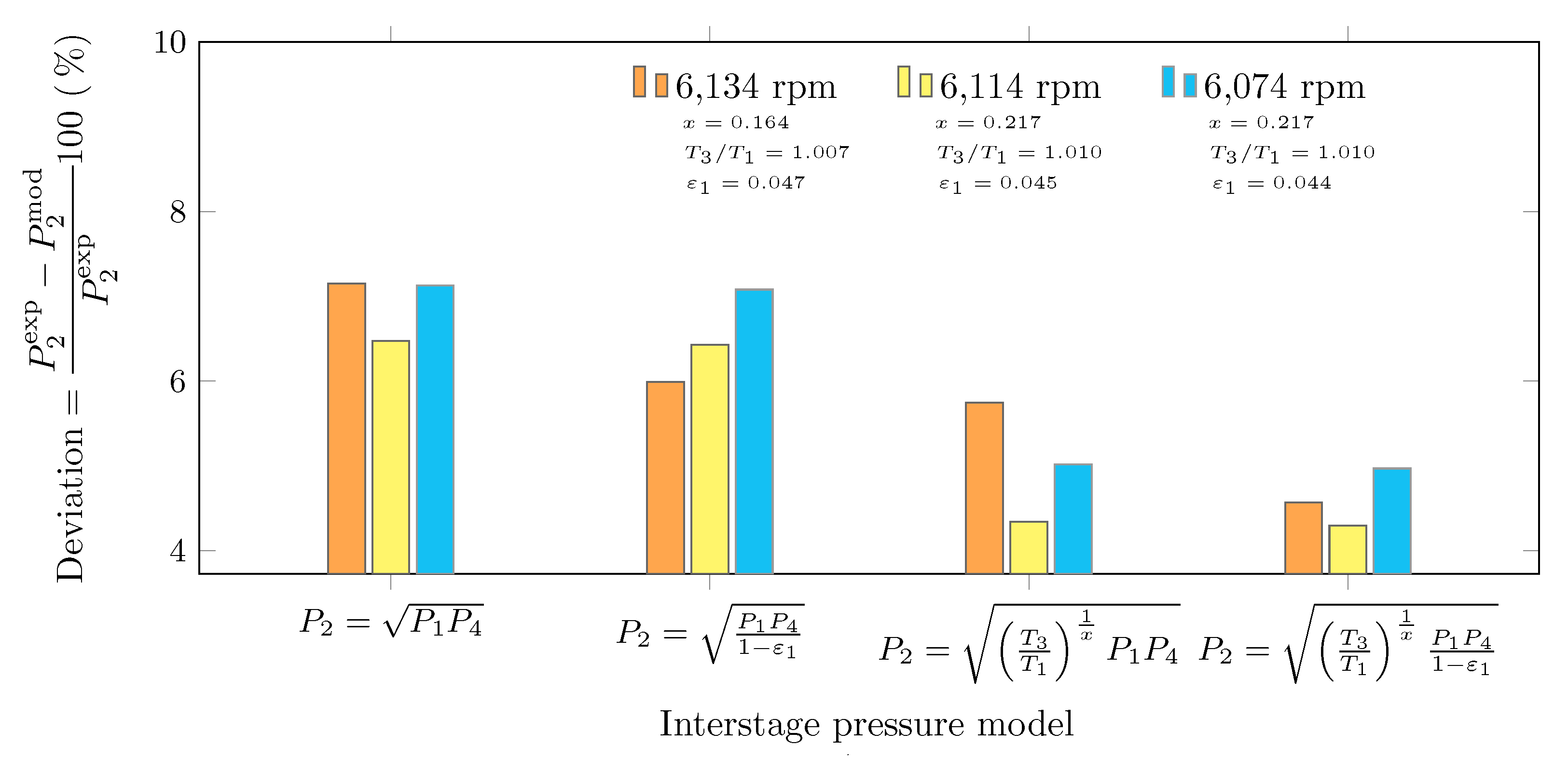
4.2. Interstage Pressure Estimation of a Natural Gas Compression System
- , same suction temperatures () and no pressure drops in the intercooler ();
- , same suction temperatures () and pressure drops in the intercooler;
- , different suction temperatures () and no pressure drops in the intercooler ();
- , different suction temperatures () and pressure drops in the intercooler;
- , different suction temperatures () and pressure drops in the intercooler.
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| specific heat at constant pressure, kJ kg K | |
| specific heat at constant volume, kJ kg K | |
| K | real constant defined by for |
| compression stages | |
| P | pressures, bar |
| R | specific gas constant, kJ kg K |
| s | specific entropy, kJ kg K |
| T | temperature, K or C |
| w | specific work, kJ kg |
| x | |
| Greek symbols | |
| , K | |
| drop or increment | |
| pressure drop coefficient across the j-intercooler, | |
| geometric mean for the set | |
| adiabatic index or specific heat ratio | |
| efficiency | |
| pressure ratio | |
| arithmetic mean for the set , K | |
| geometric mean for the set , K | |
| Subscripts | |
| c | compressor |
| d | discharge state |
| thermodynamic states | |
| s | suction state |
| isentropic compression | |
Appendix A. Optimal Interstage Pressures in Terms of Their Predecessor and Successor Pressures
Appendix B. Optimal Interstage Pressures Obtained by Successive Substitutions
Appendix C. Induction Proof of Equation (A4)
- Base case: When , Equation (A4) corresponds to Equation (7), proving Equation (A4) is true for .
- Induction hypothesis: In this step, we assume Equation (A4) is valid for k.
- Inductive step: When , Equation (7) raised to the power of becomesThe substitution of Equation (A4), corresponding to the induction hypothesis, into the left-hand side of Equation (A10) leads toAfter performing some algebraic steps in the above equation, we obtain the following expression:Thus, Equation (A4) holds for , and the proof of induction step is complete.
Appendix D. Induction proof of Equation (A7)
- Base case: When and , Equation (A4) corresponds to Equation (A7), proving Equation (A7) holds for .
- Induction hypothesis: In this step, we assume Equation (A7) is valid for m.
- Inductive step: For , Equation (A6) becomesRaising Equation (A7), corresponding to the induction hypothesis, to the power of , leads toSubstituting Equation (A7) into the left-hand side of Equation (A15)After carrying out some algebra with the above equation, we derive the following expression:Raising Equation (A16) to the power of , we may writeThus, Equation (A7) holds for , and the proof of induction step is complete.
Appendix E. Two-Stage Compression System With Intercooling
| 6134 rpm | 6114 rpm | 6074 rpm | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T (°C) | P (bar) | ρ | cp | MW | Z (-) | T (°C) | P (bar) | ρ | cp | MW | Z (-) | T (°C) | P (bar) | ρ | cp | MW | Z (-) | ||
| 1 | 5.52 | 33 | 10.58 | 10.16 | 1.45 | 26.54 | 0.98 | 33 | 10.43 | 9.99 | 1.45 | 26.54 | 0.98 | 34 | 10.59 | 10.14 | 1.45 | 26.54 | 0.98 |
| 2 | 5.52 | 144.1 | 31.42 | 23.51 | 1.64 | 26.54 | 0.99 | 142.4 | 30.44 | 22.85 | 1.63 | 26.54 | 0.99 | 142.2 | 30.50 | 22.9 | 1.63 | 26.54 | 0.99 |
| 2’ | 5.52 | 35 | 30.65 | 32.38 | 1.53 | 26.54 | 0.95 | 36 | 30.41 | 31.98 | 1.53 | 26.54 | 0.95 | 37 | 30.47 | 31.92 | 1.53 | 26.54 | 0.95 |
| 3 | 5.50 | 35 | 30.65 | 32.28 | 1.52 | 26.58 | 0.95 | 36 | 30.41 | 31.89 | 1.52 | 26.58 | 0.95 | 37 | 30.47 | 31.83 | 1.52 | 26.58 | 0.95 |
| 4 | 5.50 | 135.2 | 80.49 | 63.53 | 1.71 | 26.58 | 0.98 | 133.8 | 77.76 | 61.58 | 1.70 | 26.58 | 0.98 | 132.1 | 75.76 | 60.26 | 1.70 | 26.58 | 0.98 |
References
- Larralde, E.; Ocampo, R. Selection of gas compressors: Part 1. World Pumps 2011, 2011, 24–28. [Google Scholar] [CrossRef]
- Gupta, V.; Prasad, M. Optimum thermodynamic performance of three-stage refrigerating systems. Int. J. Refrig. 1983, 6, 103–107. [Google Scholar] [CrossRef]
- Chang, H.M. A thermodynamic review of cryogenic refrigeration cycles for liquefaction of natural gas. Cryogenics 2015, 72, 127–147. [Google Scholar] [CrossRef]
- Zhang, Z.; Tong, L.; Wang, X. Thermodynamic analysis of double-stage compression transcritical CO2 refrigeration cycles with an expander. Entropy 2015, 17, 2544–2555. [Google Scholar] [CrossRef] [Green Version]
- Cipollone, R.; Bianchi, G.; Di Battista, D.; Contaldi, G.; Murgia, S. Model based design of an intercooled dual stage sliding vane rotary compressor system. IOP Conf. Ser. Mater. Sci. Eng. 2015, 90, 012035. [Google Scholar] [CrossRef] [Green Version]
- Vadasz, P.; Weiner, D. The optimal intercooling of compressors by a finite number of intercoolers. J. Energy Resour. Technol. 1992, 114, 255. [Google Scholar] [CrossRef]
- Desai, M.G. Specifying Compressor. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 7–10 November 2016; Society of Petroleum Engineers: Richardson, TX, USA, 2016. [Google Scholar]
- Gosney, W.B. Principles of Refrigeration; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Edgar, T.F.; Himmelblau, D.M.; Lasdon, L.S. Optimization of Chemical Processes; McGraw-Hill: New York, NY, USA, 2001. [Google Scholar]
- Jekel, T.B.; Reindl, D.T. Single-or two-stage compression. ASHRAE J. 2008, 50, 46–51. [Google Scholar]
- Özgür, A.E. The performance analysis of a two-stage transcritical CO2 cooling cycle with various gas cooler pressures. Int. J. Energy Res. 2008, 32, 1309–1315. [Google Scholar] [CrossRef]
- Hernández, A.C.; Roco, J.; Medina, A. Power and efficiency in a regenerative gas-turbine cycle with multiple reheating and intercooling stages. J. Phys. D Appl. Phys. 1996, 29, 1462. [Google Scholar] [CrossRef]
- López-Paniagua, I.; Rodríguez-Martín, J.; Sánchez-Orgaz, S.; Roncal-Casano, J.J. Step by Step Derivation of the Optimum Multistage Compression Ratio and an Application Case. Entropy 2020, 22, 678. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.A. Frozen Food Science and Technology; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Ibarz, A.; Barbosa-Canovas, G.V. Introduction to Food Process Engineering; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Mbarek, W.H.; Tahar, K.; Ammar, B.B. Energy Efficiencies of Three Configurations of Two-Stage Vapor Compression Refrigeration Systems. Arab. J. Sci. Eng. 2016, 41, 2465–2477. [Google Scholar] [CrossRef]
- Pitarch, M.; Navarro-Peris, E.; Gonzalvez, J.; Corberan, J. Analysis and optimisation of different two-stage transcritical carbon dioxide cycles for heating applications. Int. J. Refrig. 2016, 70, 235–242. [Google Scholar] [CrossRef]
- Manole, D. On the optimum inter-stage parameters for CO2 transcritical systems. In Proceedings of the 7th IIR Gustav Lorentzen Conference on Natural Working Refrigerants, Trondheim, Norway, 29–31 May 2006. [Google Scholar]
- Romeo, L.M.; Bolea, I.; Lara, Y.; Escosa, J.M. Optimization of intercooling compression in CO2′ capture systems. Appl. Therm. Eng. 2009, 29, 1744–1751. [Google Scholar] [CrossRef] [Green Version]
- Srinivasan, K. Identification of optimum inter-stage pressure for two-stage transcritical carbon dioxide refrigeration cycles. J. Supercrit. Fluids 2011, 58, 26–30. [Google Scholar] [CrossRef]
- Lugo-Leyte, R.; Zamora, M.J.M.; Salazar-Pereyra, M.; Toledo-Velázquez, M. Relaciones de presiones óptimas de los ciclos complejos de las turbinas de gas. Inf. Tecnol. 2009, 20, 137–151. [Google Scholar] [CrossRef]
- Lewins, J.D. Optimising an intercooled compressor for an ideal gas model. Int. J. Mech. Eng. Educ. 2003, 31, 189–200. [Google Scholar] [CrossRef]
- Azizifar, S.; Banooni, S. Modeling and optimization of industrial multistage compressed air system using actual variable effectiveness in hot regions. Adv. Mech. Eng. 2016, 8, 1687814016647231. [Google Scholar] [CrossRef] [Green Version]

| Component | CH4 | C2H6 | C3H8 | iC4H10 | nC4H10 | iC5H12 | N2 | O2 | H2O | CO2 | H2S |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.3038 | 0.0594 | 0.0328 | 0.0043 | 0.0126 | 0.0036 | 0.543 | 0.0019 | 0.007 | 0.015 | 0.0044 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lugo-Méndez, H.; Lopez-Arenas, T.; Torres-Aldaco, A.; Torres-González, E.V.; Sales-Cruz, M.; Lugo-Leyte, R. Interstage Pressures of a Multistage Compressor with Intercooling. Entropy 2021, 23, 351. https://doi.org/10.3390/e23030351
Lugo-Méndez H, Lopez-Arenas T, Torres-Aldaco A, Torres-González EV, Sales-Cruz M, Lugo-Leyte R. Interstage Pressures of a Multistage Compressor with Intercooling. Entropy. 2021; 23(3):351. https://doi.org/10.3390/e23030351
Chicago/Turabian StyleLugo-Méndez, Helen, Teresa Lopez-Arenas, Alejandro Torres-Aldaco, Edgar Vicente Torres-González, Mauricio Sales-Cruz, and Raúl Lugo-Leyte. 2021. "Interstage Pressures of a Multistage Compressor with Intercooling" Entropy 23, no. 3: 351. https://doi.org/10.3390/e23030351
APA StyleLugo-Méndez, H., Lopez-Arenas, T., Torres-Aldaco, A., Torres-González, E. V., Sales-Cruz, M., & Lugo-Leyte, R. (2021). Interstage Pressures of a Multistage Compressor with Intercooling. Entropy, 23(3), 351. https://doi.org/10.3390/e23030351






