Effect of Inter-System Coupling on Heat Transport in a Microscopic Collision Model
Abstract
:1. Introduction
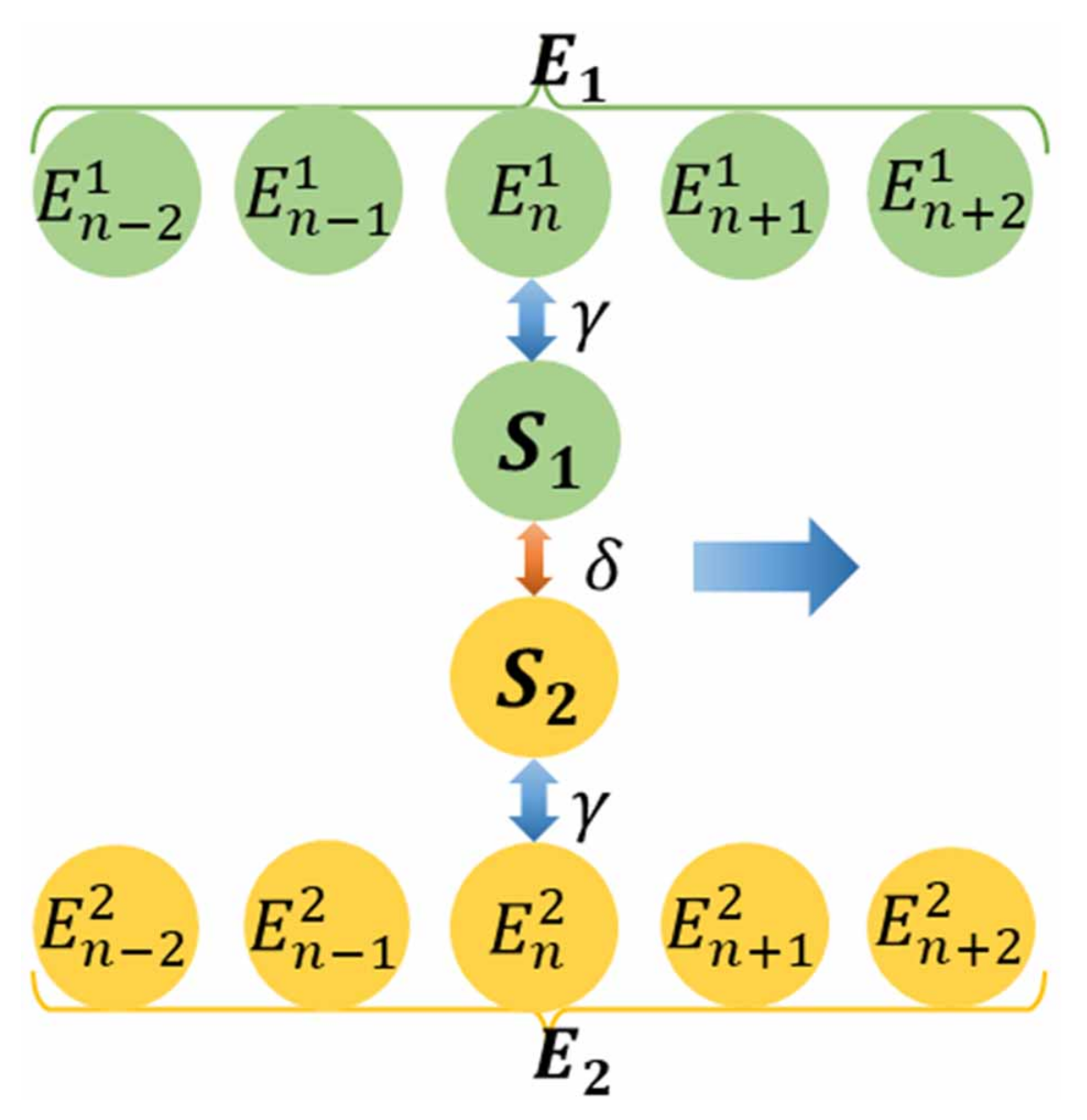
2. Model and Methods
3. Symmetric System
3.1. Heat Current
3.2. Trace Distance
3.3. Quantum Discord
- and .
- and .
- and .
4. Asymmetric System
4.1. Off-Resonant Interacting Qubits
4.2. Anisotropic Interacting Qubits
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weiss, U. Quantum Dissipative Systems; World Scientific: Singapore, 2000. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Levy, A.; Kosloff, R. The local approach to quantum transport may violate the second law of thermodynamics. Europhys. Lett. 2014, 107, 20004. [Google Scholar] [CrossRef] [Green Version]
- Werlang, T.; Valente, D. Heat transport between two pure-dephasing reservoirs. Phys. Rev. E 2015, 91, 012143. [Google Scholar] [CrossRef] [Green Version]
- De Chiara, G.; Landi, G.; Hewgill, A.; Reid, B.; Ferraro, A.; Roncaglia, A.J.; Antezza, M. Reconciliation of quantum local master equations with thermodynamics. New J. Phys. 2018, 20, 113024. [Google Scholar] [CrossRef]
- Deçordi, G.L.; Vidiella-Barranco, A. Two coupled qubits interacting with a thermal bath: A comparative study of different models. Opt. Commun. 2017, 387, 366–376. [Google Scholar] [CrossRef] [Green Version]
- Naseem, T.M.; Xuereb, A.; Müstecaplıoğlu, Ö.E. Thermodynamic consistency of the optomechanical master equation. Phys. Rev. A 2018, 98, 052123. [Google Scholar] [CrossRef] [Green Version]
- Čápek, V. Zeroth and second laws of thermodynamics simultaneously questioned in the quantum microworld. Eur. Phys. J. B 2002, 25, 101–113. [Google Scholar] [CrossRef]
- Novotný, T. Investigation of apparent violation of the second law of thermodynamics in quantum transport studies. Europhys. Lett. 2002, 59, 648. [Google Scholar] [CrossRef] [Green Version]
- Betzholz, R.; Torres, J.M.; Bienert, M. Quantum optical master equation for solid-state quantum emitters. Phys. Rev. A 2014, 90, 063818. [Google Scholar] [CrossRef] [Green Version]
- Plenio, M.B.; Almeida, J.; Huelga, S.F. Origin of long-lived oscillations in 2D-spectra of a quantum vibronic model: Electronic versus vibrational coherence. J. Chem. Phys. 2013, 139, 235102. [Google Scholar] [CrossRef] [Green Version]
- Atalaya, J.; Gorelik, L.Y. Spintronics-based mesoscopic heat engine. Phys. Rev. B 2012, 85, 245309. [Google Scholar] [CrossRef] [Green Version]
- Mohseni, M.; Rebentrost, P.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum walks in photosynthetic energy transfer. J. Chem. Phys. 2008, 129, 174106. [Google Scholar] [CrossRef] [Green Version]
- Wilson-Rae, I.; Zoller, P.; Imamoḡlu, A. Laser Cooling of a Nanomechanical Resonator Mode to its Quantum Ground State. Phys. Rev. Lett. 2004, 92, 075507. [Google Scholar] [CrossRef] [Green Version]
- Scali, S.; Anders, J.; Correa, L.A. Local master equations bypass the secular approximation. arXiv 2020, arXiv:2009.11324. [Google Scholar]
- Gonzlez, J.O.; Correa, L.A.; Nocerino, G.; Palao, J.P.; Alonso, D.; Adesso, G. Testing the Validity of the ‘Local’ and ‘Global’ GKLS Master Equations on an Exactly Solvable Model. Open Syst. Inf. Dyn. 2017, 24, 1740010. [Google Scholar] [CrossRef]
- Du, J.Y.; Zhang, F.L. Perturbative Treatment for Stationary State of Local Master Equation. Commun. Theor. Phys. 2018, 70, 038. [Google Scholar] [CrossRef] [Green Version]
- Manrique, P.D.; Rodri-guez, F.; Quiroga, L.; Johnson, N.F. Nonequilibrium Quantum Systems: Divergence between Global and Local Descriptions. Adv. Condens. Matter Phys. 2015, 19, 615727. [Google Scholar] [CrossRef] [Green Version]
- Hofer, P.P.; Perarnau-Llobet, M.; Miranda, L.D.M.; Haack, G.; Silva, R.; Brask, J.B.; Brunner, N. Markovian master equations for quantum thermal machines: Local versus global approach. New J. Phys. 2017, 19, 123037. [Google Scholar] [CrossRef]
- Trushechkin, A.S.; Volovich, I.V. Perturbative treatment of inter-site couplings in the local description of open quantum networks. Europhys. Lett. 2016, 113, 30005. [Google Scholar] [CrossRef] [Green Version]
- Wichterich, H.; Henrich, M.J.; Breuer, H.P.; Gemmer, J.; Michel, M. Modeling heat transport through completely positive maps. Phys. Rev. E 2007, 76, 031115. [Google Scholar] [CrossRef] [Green Version]
- Benatti, F.; Floreanini, R.; Memarzadeh, L. Bath-assisted transport in a three-site spin chain: Global versus local approach. Phys. Rev. A 2020, 102, 042219. [Google Scholar] [CrossRef]
- Barra, F. The thermodynamic cost of driving quantum systems by their boundaries. Sci. Rep. 2015, 5, 14873. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cattaneo, M.; Giorgi, G.L.; Maniscalco, S.; Zambrini, R. Local versus global master equation with common and separate baths: Superiority of the global approach in partial secular approximation. New J. Phys. 2019, 21, 113045. [Google Scholar] [CrossRef]
- Farina, D.; Filippis, G.D.; Cataudella, V.; Polini, M.; Giovannetti, V. Going beyond local and global approaches for localized thermal dissipation. Phys. Rev. A 2020, 102, 052208. [Google Scholar] [CrossRef]
- Hewgill, A.; Chiara, G.D.; Imparato, A. Quantum thermodynamically consistent local master equations. Phys. Rev. Res. 2021, 3, 013165. [Google Scholar] [CrossRef]
- Wang, J.S.; Wang, J.; Lü, J.T. Quantum thermal transport in nanostructures. Eur. J. Phys. B 2008, 62, 381. [Google Scholar] [CrossRef]
- Yan, Y.; Wu, C.Q.; Li, B. Control of heat transport in quantum spin systems. Phys. Rev. B 2009, 79, 014207. [Google Scholar] [CrossRef] [Green Version]
- Thingna, J.; García-Palacios, J.L.; Wang, J.S. Steady-state thermal transport in anharmonic systems: Application to molecular junctions. Phys. Rev. B 2012, 85, 195452. [Google Scholar] [CrossRef] [Green Version]
- Michel, M.; Hess, O.; Wichterich, H.; Gemmer, J. Transport in open spin chains: A Monte Carlo wave-function approach. Phys. Rev. B 2008, 77, 104303. [Google Scholar] [CrossRef] [Green Version]
- Manzano, D.; Tiersch, M.; Asadian, A.; Briegel, H.J. Quantum transport efficiency and Fourier’s law. Phys. Rev. E 2012, 86, 061118. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Agarwalla, B.K.; Li, B.; Wang, J.S. Cumulants of heat transfer across nonlinear quantum systems. Eur. Phys. J. B 2013, 86, 500. [Google Scholar] [CrossRef] [Green Version]
- Segal, D. Heat transfer in the spin-boson model: A comparative study in the incoherent tunneling regime. Phys. Rev. E 2014, 90, 012148. [Google Scholar] [CrossRef] [Green Version]
- Bandyopadhyay, M.; Segal, D. Quantum heat transfer in harmonic chains with self-consistent reservoirs: Exact numerical simulations. Phys. Rev. E 2011, 84, 011151. [Google Scholar] [CrossRef] [Green Version]
- He, D.; Thingna, J.; Wang, J.S.; Li, B. Quantum thermal transport through anharmonic systems: A self-consistent approach. Phys. Rev. B 2016, 94, 155411. [Google Scholar] [CrossRef] [Green Version]
- Man, Z.X.; An, N.B.; Xia, Y.J. Controlling heat flows among three reservoirs asymmetrically coupled to two two-level systems. Phys. Rev. E 2016, 94, 042135. [Google Scholar] [CrossRef]
- Guo, B.Q.; Liu, T.; Yu, C.S. Quantum thermal transistor based on qubit-qutrit coupling. Phys. Rev. E 2018, 98, 022118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Li, B. Thermal Memory: A Storage of Phononic Information. Phys. Rev. Lett. 2008, 101, 267203. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ruokola, T.; Ojanen, T.; Jauho, A.P. Thermal rectification in nonlinear quantum circuits. Phys. Rev. B 2009, 79, 144306. [Google Scholar] [CrossRef] [Green Version]
- Landi, G.T.; Novais, E.; Oliveira, M.J.; Karevski, D. Flux rectification in the quantum XXZ chain. Phys. Rev. E 2014, 90, 042142. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pons, M.; Cuı, Y.Y.; Ruschhaupt, A.; Simón, M.A.; Muga, J.G. Local rectification of heat flux. Europhys. Lett. 2017, 119, 64001. [Google Scholar] [CrossRef] [Green Version]
- Kargi, C.; Naseem, M.T.; Opatrný, T.; Müstecaplıoğlu, Ö.E.; Kurizki, G. Quantum Optical Two-Atom Thermal Diode. Phys. Rev. E 2019, 99, 042121. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Yan, Y.H.; Wu, C.Q.; Wang, J.S.; Li, B. Reversal of thermal rectification in quantum systems. Phys. Rev. B 2016, 80, 172301. [Google Scholar] [CrossRef] [Green Version]
- Werlang, T.; Marchiori, M.A.; Cornelio, M.F.; Valente, D. Oplimal rectification in the ultrastrong coupling regime. Phys. Rev. E 2014, 89, 062109. [Google Scholar] [CrossRef] [Green Version]
- Ordonez-Miranda, J.; Ezzahri, Y.; Joulain, K. Quantum thermal diode based on two interacting spinlike systems under different excitations. Phys. Rev. E 2017, 95, 022128. [Google Scholar] [CrossRef]
- Rau, J. Relaxation Phenomena in Spin and Harmonic Oscillator Systems. Phys. Rev. 1963, 129, 1880. [Google Scholar] [CrossRef]
- Bernardes, N.K.; Carvalho, A.R.R.; Monken, C.H.; Santos, M.F. Environmental correlations and Markovian to non-Markovian transitions in collisional models. Phys. Rev. A 2014, 90, 032111. [Google Scholar] [CrossRef] [Green Version]
- Lorenzo, S.; McCloskey, R.; Ciccarello, F.; Paternostro, M.; Palma, G.M. Landauer’s Principle in Multipartite Open Quantum System Dynamics. Phys. Rev. Lett. 2015, 115, 120403. [Google Scholar] [CrossRef] [PubMed]
- Karevski, D.; Platini, T. Quantum Nonequilibrium Steady States Induced by Repeated Interactions. Phys. Rev. Lett. 2009, 102, 207207. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernardes, N.K.; Carvalho, A.R.R.; Monken, C.H.; Santos, M.F. Coarse graining a non-Markovian collisional model. Phys. Rev. A 2017, 95, 032117. [Google Scholar] [CrossRef] [Green Version]
- Benenti, G.; Palma, G.M. Reversible and irreversible dynamics of a qubit interacting with a small environment. Phys. Rev. A 2007, 75, 052110. [Google Scholar] [CrossRef] [Green Version]
- Filippov, S.N.; Piilo, J.; Maniscalco, S.; Ziman, M. Divisibility of quantum dynamical maps and collision models. Phys. Rev. A 2017, 96, 032111. [Google Scholar] [CrossRef] [Green Version]
- Giovannetti, V.; Palma, G.M. Master Equations for Correlated Quantum Channels. Phys. Rev. Lett. 2012, 108, 040401. [Google Scholar] [CrossRef] [Green Version]
- Daryanoosh, S.; Baragiola, B.Q.; Guf, T.; Gilchrist, A. Quantum master equations for entangled qubit environments. Phys. Rev. A 2018, 98, 062104. [Google Scholar] [CrossRef] [Green Version]
- Man, Z.X.; Xia, Y.J.; Franco, R.L. Validity of the Landauer principle and quantum memory effects via collisional models. Phys. Rev. A 2019, 99, 042106. [Google Scholar] [CrossRef] [Green Version]
- Manatuly, A.; Niedenzu, W.; Ancheyta, R.R.; Çakmak, B. Müstecaplıoğlu, Ö.E.; Kurizki, G. Collectively enhanced thermalization via multiqubit collisions. Phys. Rev. E 2019, 99, 042145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cattaneo, M.; Chiara, G.D.; Maniscalco, S.; Zambrini, R.; Giorgi, L.G. Collision model can effeciently simulate any multipartite Markovian quantum dynamics. arXiv 2020, arXiv:2010.13910. [Google Scholar]
- Rodrigues, F.L.S.; De ChiaraPhys, G.; Paternostro, M.; LandiRev, G.T. Thermodynamics of Weakly Coherent Collisional Models. Phys. Rev. Lett. 2019, 123, 140601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Çakmak, B.; Campbell, S.; Vacchini, B.; Müstecaplıoğlu, Ö.E.; Paternostro, M. Robust multipartite entanglement generation via a collision model. Phys. Rev. A 2018, 99, 012319. [Google Scholar] [CrossRef] [Green Version]
- Man, Z.X.; Xia, Y.J.; Franco, R.L. Temperature effects on quantum non-Markovianity via collision models. Phys. Rev. A 2018, 97, 062104. [Google Scholar] [CrossRef] [Green Version]
- McCloskey, R.; Paternostro, M. Non-Markovianity and system–environment correlations in a microscopic collision model. Phys. Rev. A 2014, 89, 052120. [Google Scholar] [CrossRef] [Green Version]
- Campbell, S.; Ciccarello, F.; Palma, G.M.; Vacchini, B. System-environment correlations and Markovian embedding of quantum non-Markovian dynamics. Phys. Rev. A 2018, 98, 012142. [Google Scholar] [CrossRef]
- Çakmak, B.; Pezzutto, M.; Paternostro, M.; Müstecaplıoğlu, Ö.E. Non-Markovianity, coherence, and system–environment correlations in a long-range collision model. Phys. Rev. A 2017, 96, 022109. [Google Scholar] [CrossRef] [Green Version]
- Beyer, K.; Luoma, K.; Strunz, W.T. Collision-model approach to steering of an open driven qubit. Phys. Rev. A 2017, 97, 032113. [Google Scholar] [CrossRef] [Green Version]
- Lorenzo, S.; Farace, A.; Ciccarello, F.; Palma, G.M.; Giovannetti, V. Heat flux and quantum correlations in dissipative cascaded systems. Phys. Rev. A 2015, 91, 022121. [Google Scholar] [CrossRef]
- Li, L.; Zou, J.; Li, H.; Xu, B.M.; Wang, Y.M.; Shao, B. Effect of coherence of nonthermal reservoirs on heat transport in a microscopic collision model. Phys. Rev. E 2018, 97, 022111. [Google Scholar] [CrossRef] [Green Version]
- Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. Quantum and Information Thermodynamics: A Unifying Framework Based on Repeated Interactions. Phys. Rev. X 2017, 7, 021003. [Google Scholar] [CrossRef] [Green Version]
- Seah, S.; Nimmrichter, S.; Scarani, V. Nonequilibrium dynamics with finite-time repeated interactions. Phys. Rev. E 2019, 99, 042103. [Google Scholar] [CrossRef] [Green Version]
- Weimear, H.; Henrich, M.J.; Rempp, F.; Schröder, H.; Mahler, G. Local effective dynamics of quantum systems: A generalized approach to work and heat. Europhys. Lett. 2008, 83, 30008. [Google Scholar] [CrossRef]
- Hossein-Nejad, H.; O’Reilly, E.J.; Olaya-Castro, A. Work, heat and entropy production in bipartite quantum systems. New J. Phys. 2015, 17, 075014. [Google Scholar] [CrossRef]
- Law, C.K. Quantum entanglement as an interpretation of bosonic character in composite two-particle systems. Phys. Rev. A 2005, 71, 034306. [Google Scholar] [CrossRef] [Green Version]
- Lasmar, Z.; Sajna, A.S.; Lee, S.Y.; Kurzyński, P. Dynamical stability of composite quantum particles: When entanglement is enough and when interaction is needed. Phys. Rev. A 2018, 98, 062105. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.Z.; Li, C.X.; Nie, L.Y.; Li, J.F. Classical correlation and quantum discord mediated by cavity in two coupled qubits. J. Phys. B 2011, 44, 015503. [Google Scholar] [CrossRef]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, F.; Zou, J.; Li, L.; Li, H.; Shao, B. Effect of Inter-System Coupling on Heat Transport in a Microscopic Collision Model. Entropy 2021, 23, 471. https://doi.org/10.3390/e23040471
Tian F, Zou J, Li L, Li H, Shao B. Effect of Inter-System Coupling on Heat Transport in a Microscopic Collision Model. Entropy. 2021; 23(4):471. https://doi.org/10.3390/e23040471
Chicago/Turabian StyleTian, Feng, Jian Zou, Lei Li, Hai Li, and Bin Shao. 2021. "Effect of Inter-System Coupling on Heat Transport in a Microscopic Collision Model" Entropy 23, no. 4: 471. https://doi.org/10.3390/e23040471





