Variable-Order Fractional Models for Wall-Bounded Turbulent Flows
Abstract
:1. Introduction
2. Variable-Order Fractional Models for Turbulent Flows
2.1. Turbulent Channel Flow and Pipe Flow
2.1.1. One-Sided Fractional Derivative Modeling
2.1.2. Numerical Method
2.2. Two-Sided Turbulent Channel Flow
2.2.1. Fractional Modeling in Divergence Form
2.2.2. Numerical Method
2.3. Turbulent Boundary Layer and Couette Flow
Numerical Method
3. Numerical Results
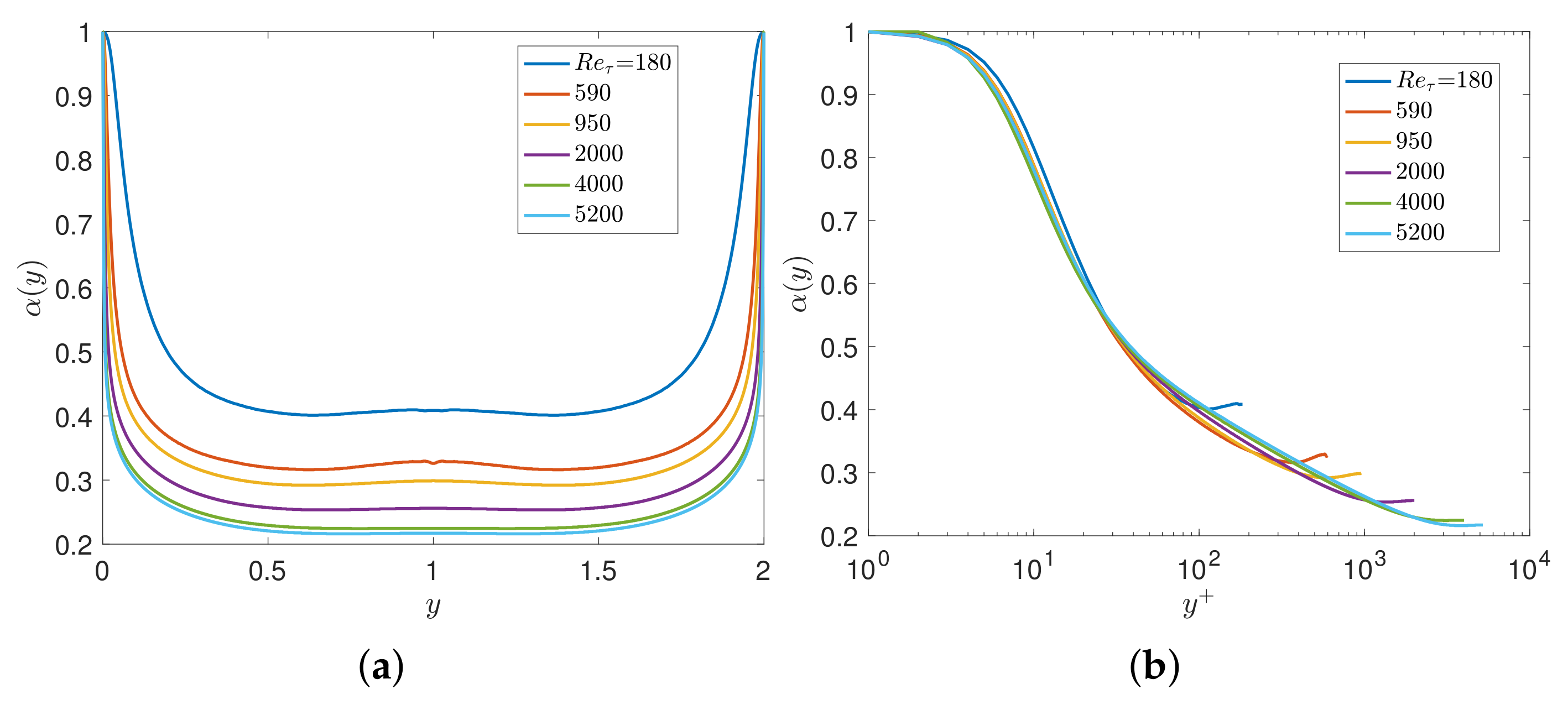
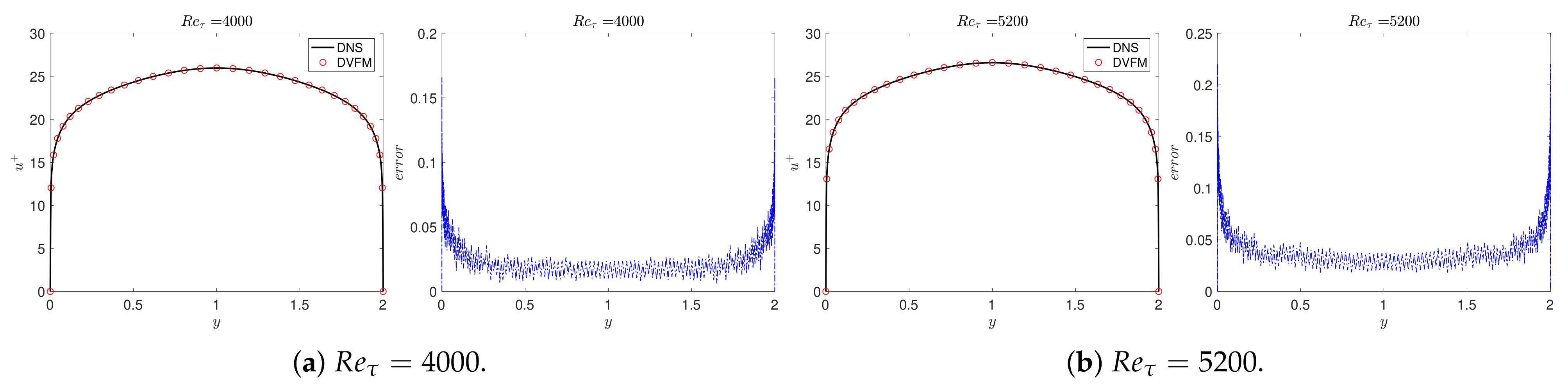
3.1. Channel Flow
3.1.1. Numerical Results of the One-Sided Models
3.1.2. Numerical Results of the Two-Sided Models
3.2. Turbulent Pipe Flow
3.3. Turbulent Couette Flow
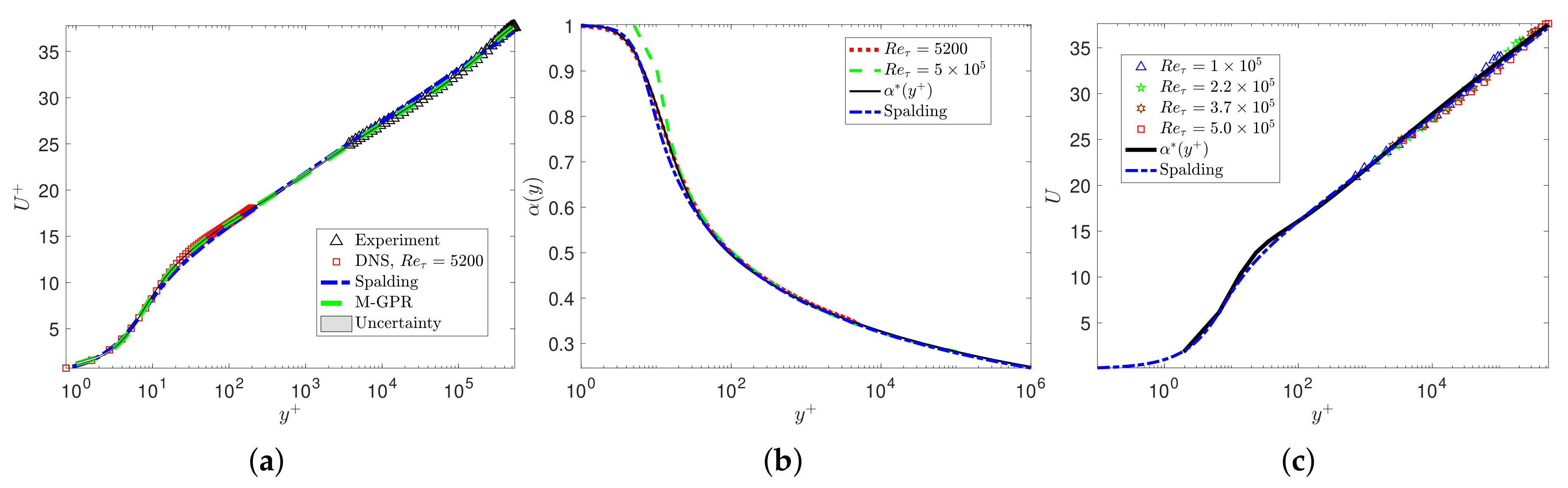
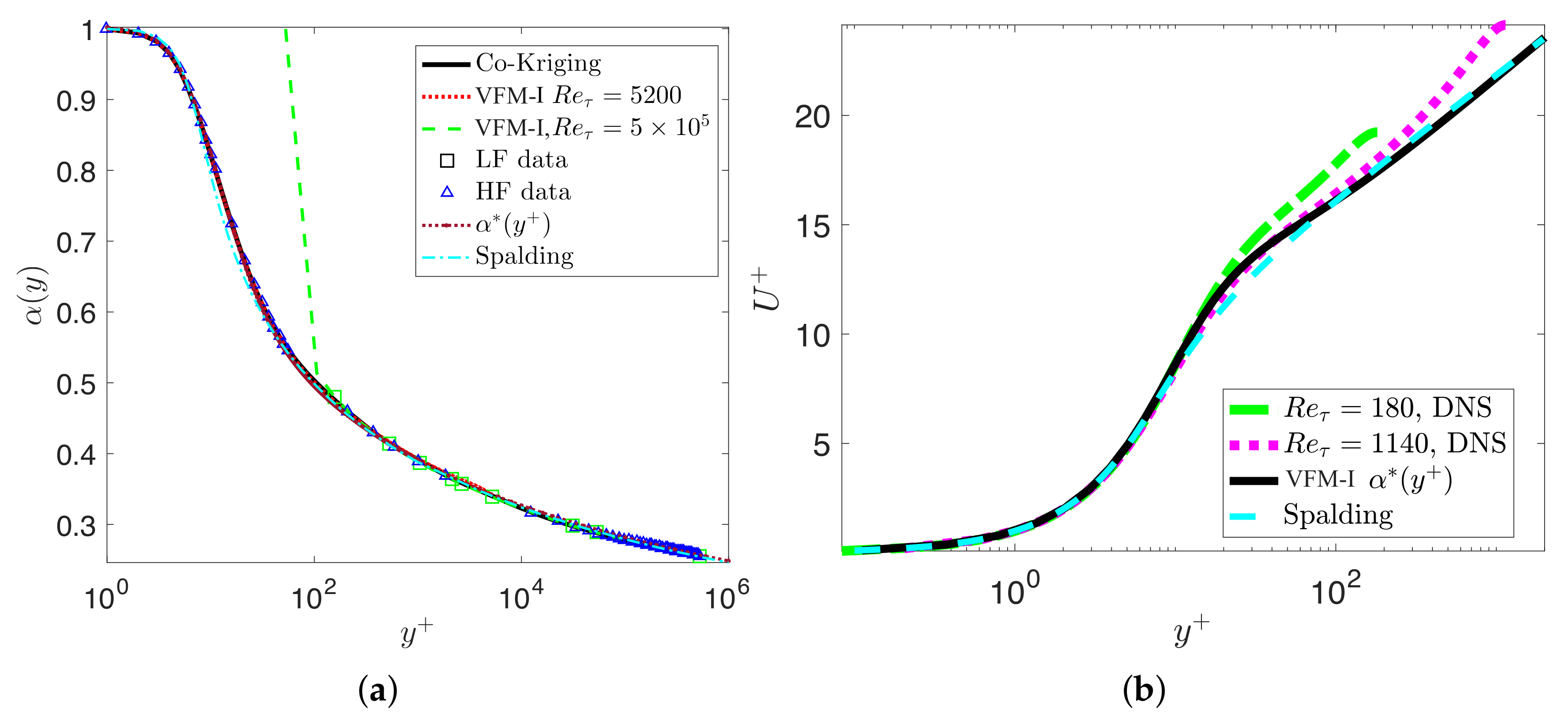
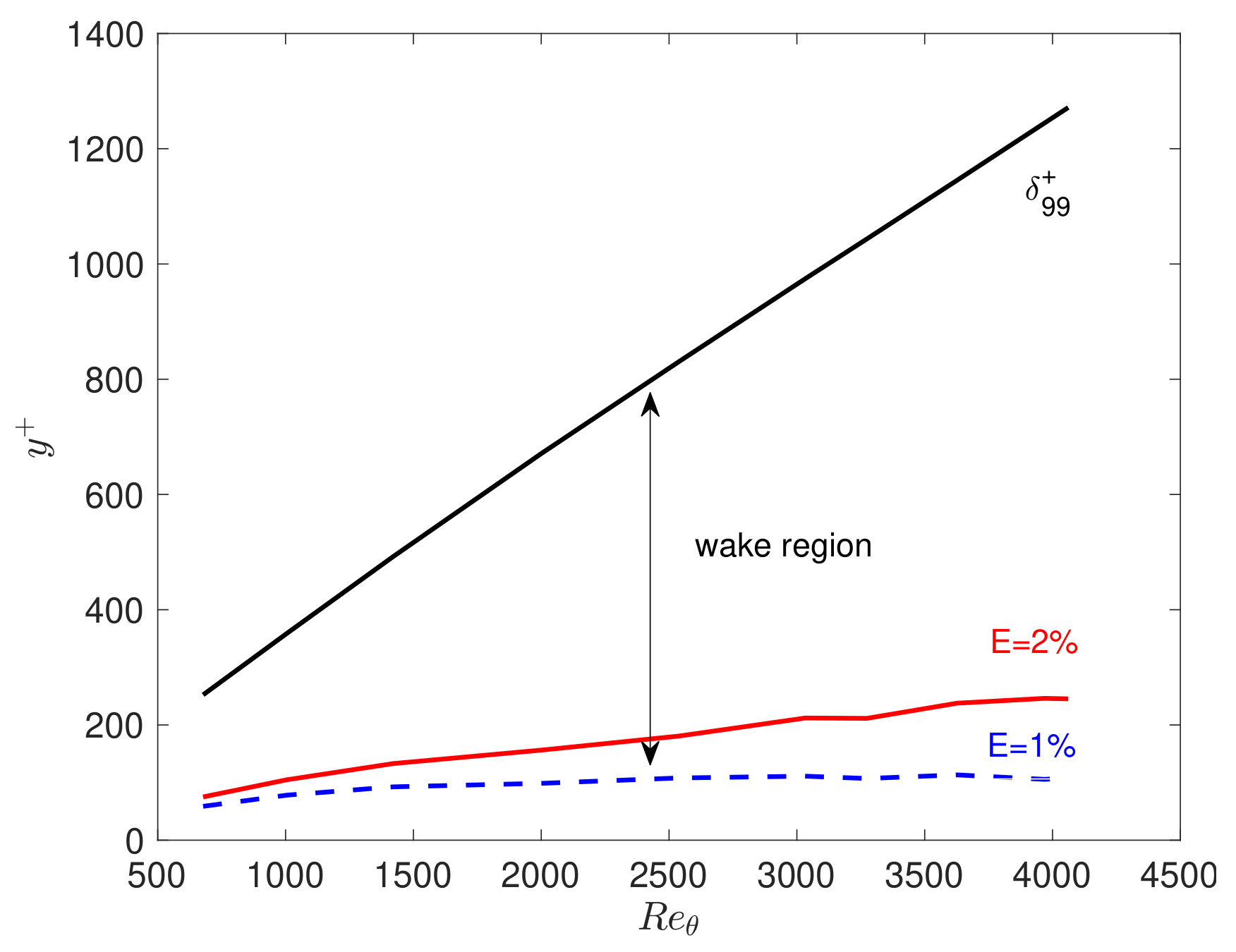
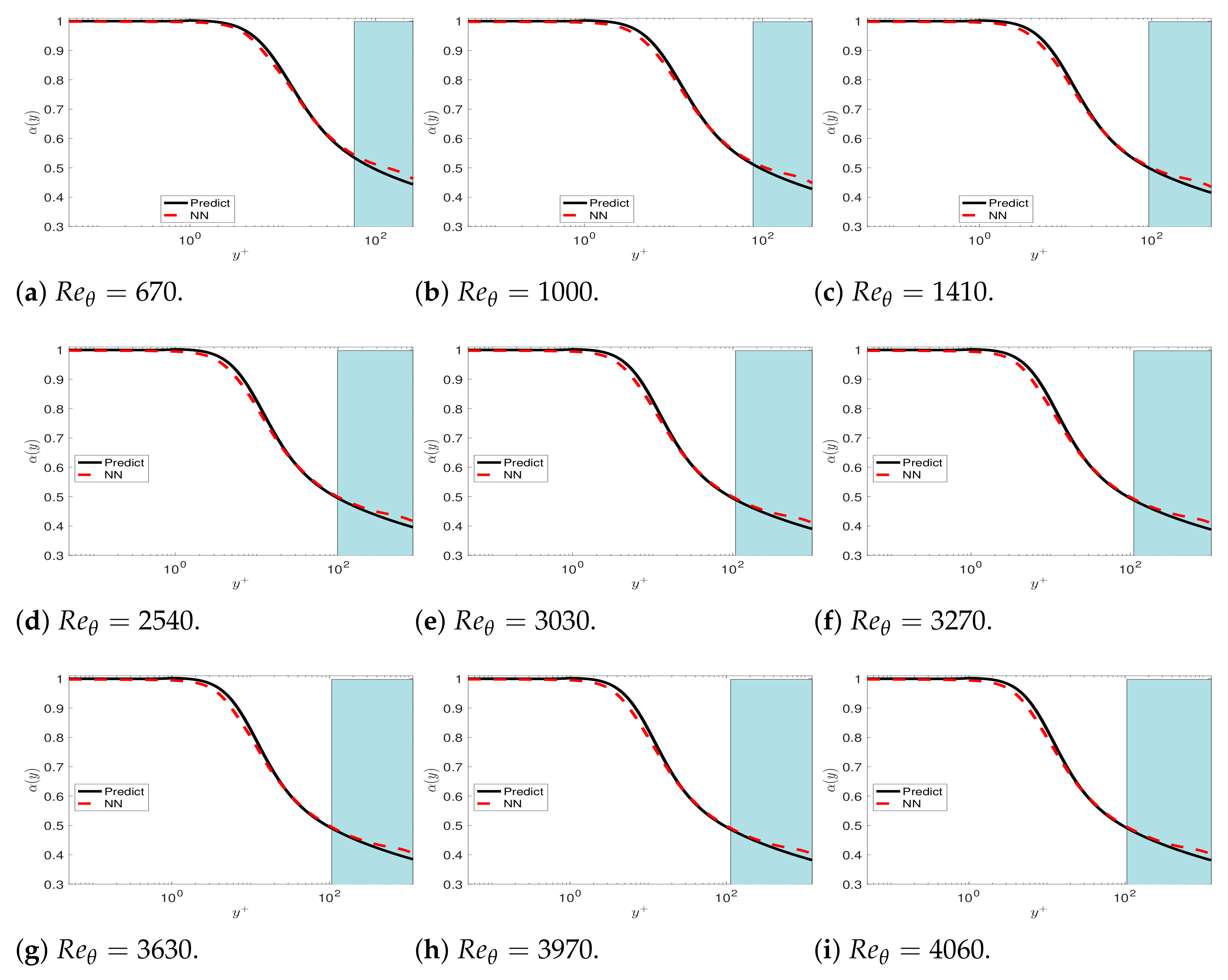
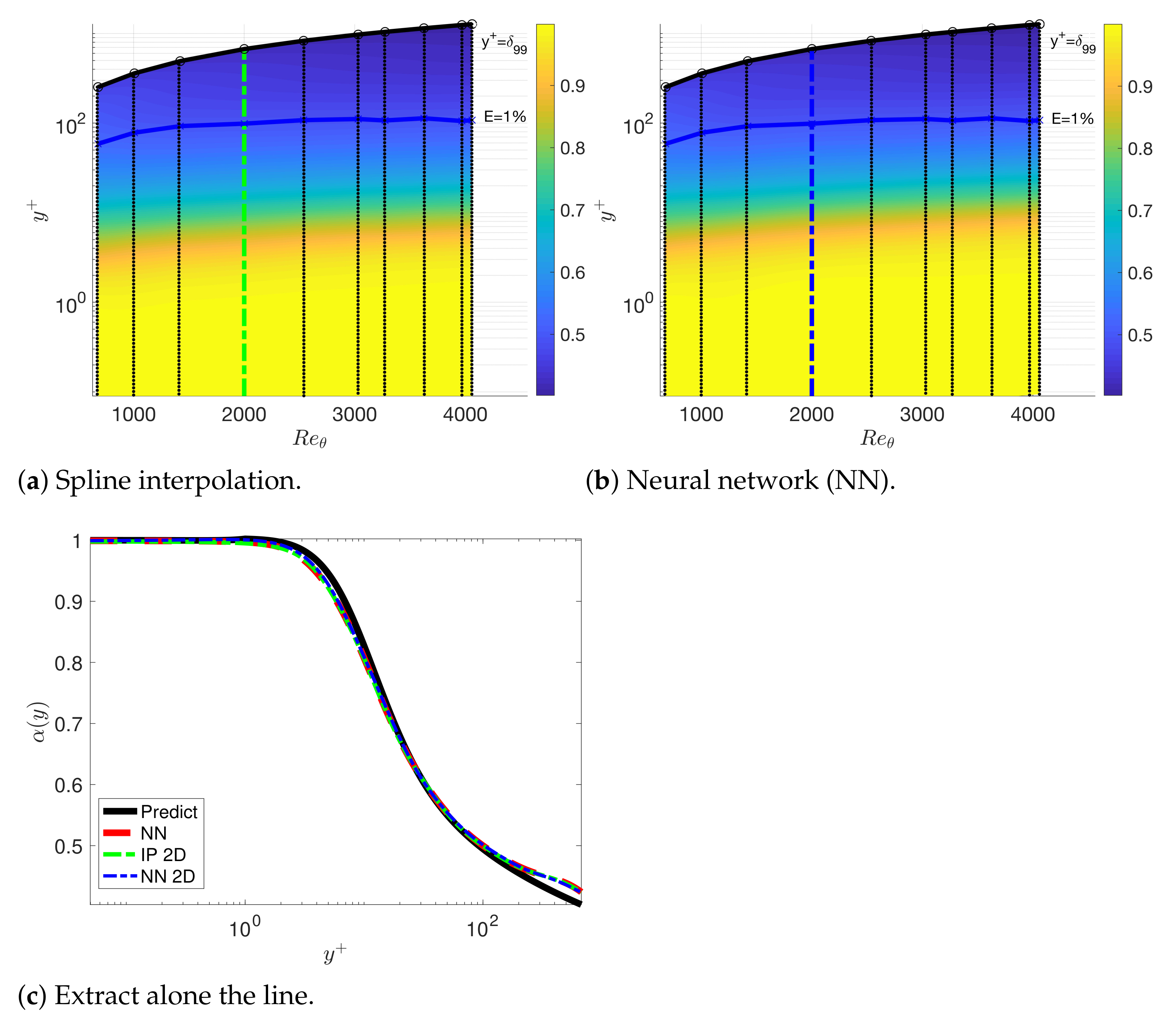
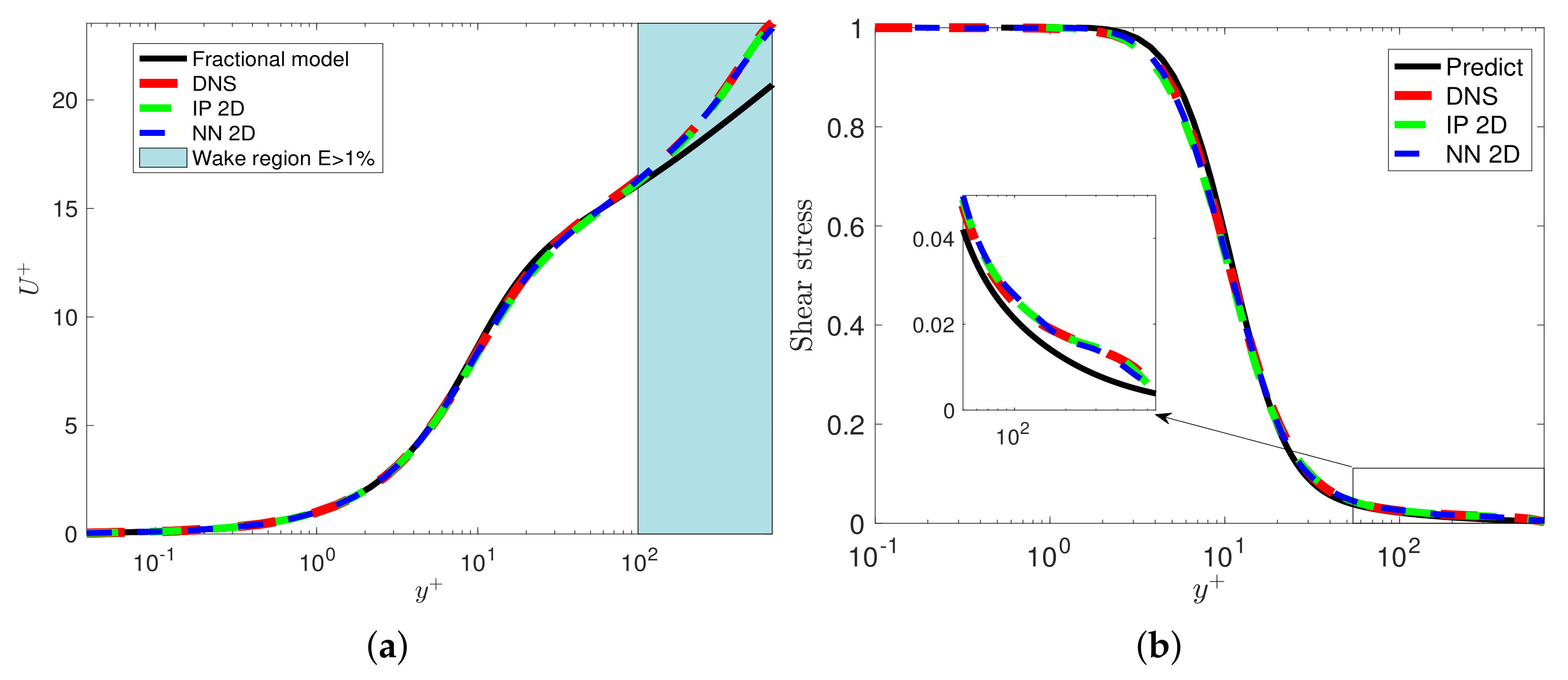
3.4. Turbulent Boundary Layer Flow
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reynolds, O. On the dynamical theory of incompressible viscous fluids and the determination of the criterion. Philos. Trans. R. Soc. Lond. A 1895, 186, 123–164. [Google Scholar]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Prandtl, L. Bericht uber Untersuchungen zur ausgebildeten Turbulenz. Z. Angew. Math. Mech. 1925, 5, 136–139. [Google Scholar] [CrossRef]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. R. Soc. Lond. 1926, 110, 709–737. [Google Scholar]
- Kraichnan, R.H. Direct-Interaction Approximation for Shear and Thermally Driven Turbulence. Phys. Fluids 1964, 7, 1048–1062. [Google Scholar] [CrossRef]
- Prandtl, L. Bemerkungen zur Theorie der freien Turbulenz. ZAMM-J. Appl. Math. Mech. Angew. Math. Mech. 1942, 22, 241–243. [Google Scholar] [CrossRef]
- Egolf, P.W.; Hutter, K. A nonlocal zero-Equation turbulence model and a deficit-power law of the wall with a dynamical critical phenomenon. Proc. Appl. Math. Mech. 2016, 16, 889–890. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance III: The diffusion limit. Mathematical finnance. Trends Math. Birkhäuser 2001, 2001, 171–180. [Google Scholar]
- Shlesinger, M.; West, B.; Klafter, J. Lévy dynamics of enhanced diffusion: Application to turbulence. Phys. Rev. Lett. 1987, 58, 1100. [Google Scholar] [CrossRef]
- Egolf, P.W.; Hutter, K. Fractional Turbulence Models. In Progress in Turbulence VII; Springer: Berlin/Heidelberg, Germany, 2017; pp. 123–131. [Google Scholar]
- Chen, W. A speculative study of 2/3-order fractional Laplacian modeling of turbulence: Some thoughts and conjectures. Chaos Interdiscip. J. Nonlinear Sci. 2006, 16, 023126. [Google Scholar] [CrossRef]
- Epps, B.P.; Cushman-Roisin, B. Turbulence modeling via the fractional Laplacian. arXiv 2018, arXiv:1803.05286. [Google Scholar]
- Samiee, M.; Akhavan-Safaei, A.; Zayernouri, M. A fractional subgrid-scale model for turbulent flows: Theoretical formulation and a priori study. Phys. Fluids 2020, 32, 055102. [Google Scholar] [CrossRef]
- George, W.K. Is there a universal log law for turbulent wall-bounded flows? Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2007, 365, 789–806. [Google Scholar] [CrossRef]
- Lischke, A.; Pang, G.; Gulian, M.; Song, F.; Glusa, C.; Zheng, X.; Mao, Z.; Cai, W.; Meerschaert, M.M.; Ainsworth, M.; et al. What is the fractional Laplacian? A comparative review with new results. J. Comput. Phys. 2020, 404, 109009. [Google Scholar] [CrossRef]
- Song, F.; Karniadakis, G.E. A universal fractional model of wall-turbulence. arXiv 2018, arXiv:1808.10276. [Google Scholar]
- Mehta, P.P.; Pang, G.; Song, F.; Karniadakis, G.E. Discovering a universal variable-order fractional model for turbulent Couette flow using a physics-informed neural network. Fract. Calc. Appl. Anal. 2019, 22, 1675–1688. [Google Scholar] [CrossRef]
- Marusic, I.; McKeon, B.; Monkewitz, P.; Nagib, H.; Smits, A.; Sreenivasan, K. Wall-bounded turbulent flows at high Reynolds numbers: Recent advances and key issues. Phys. Fluids 2010, 22, 065103. [Google Scholar] [CrossRef]
- Johnson, P.L.; Meneveau, C. Turbulence intermittency in a multiple-time-scale Navier-Stokes-based reduced model. Phys. Rev. Fluids 2017, 2, 072601. [Google Scholar] [CrossRef]
- Sabzikar, F.; Meerschaert, M.M.; Chen, J. Tempered fractional calculus. J. Comput. Phys. 2015, 293, 14–28. [Google Scholar] [CrossRef] [Green Version]
- Lin, Y.; Xu, C. Finite difference/spectral approximations for the time-fractional diffusion equation. J. Comput. Phys. 2007, 225, 1533–1552. [Google Scholar] [CrossRef]
- Lee, M.; Moser, R.D. Direct numerical simulation of turbulent channel flow up to Reτ=5200. J. Fluid Mech. 2015, 774, 395–415. [Google Scholar] [CrossRef]
- White, F.M. Viscous Fluid Flow; MacGraw-Hill: New York, NY, USA, 1991; pp. 335–393. [Google Scholar]
- Tang, Y. A Nested-LES Approach for Computation of High-Reynolds Number, Equilibrium and Non-Equilibrium Turbulent Wall-Bounded Flows. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2016. [Google Scholar]
- Schultz, M.P.; Flack, K.A. Reynolds-number scaling of turbulent channel flow. Phys. Fluids 2013, 25, 025104. [Google Scholar] [CrossRef] [Green Version]
- Comte-Bellot, G. Turbulent Flow between Two Parallel Walls. Ph.D. Thesis, University of Grenoble, Grenoble, France, 1963. [Google Scholar]
- Zagarola, M.V.; Smits, A.J. Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 1998, 373, 33–79. [Google Scholar] [CrossRef]
- McKeon, B.J.; Smits, A.J. Static pressure correction in high Reynolds number fully developed turbulent pipe flow. Meas. Sci. Technol. 2002, 13, 1608. [Google Scholar] [CrossRef] [Green Version]
- Kennedy, M.C.; O’Hagan, A. Predicting the output from a complex computer code when fast approximations are available. Biometrika 2000, 87, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Wu, X.; Moin, P. A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 2008, 608, 81–112. [Google Scholar] [CrossRef]
- Liu, C.H. Turbulent plane Couette flow and scalar transport at low Reynolds number. J. Heat Transf. 2003, 125, 988–998. [Google Scholar] [CrossRef]
- Avsarkisov, V.; Hoyas, S.; Oberlack, M.; García-Galache, J. Turbulent plane Couette flow at moderately high Reynolds number. J. Fluid Mech. 2014, 751. [Google Scholar] [CrossRef]
- Robertson, J.M.; Johnson, H.F. Turbulence structure in plane Couette flow. J. Eng. Mech. Div. 1970, 96, 1171–1182. [Google Scholar] [CrossRef]
- Schlatter, P.; Örlü, R. Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 2010, 659, 116. [Google Scholar] [CrossRef]
- Schlatter, P.; Li, Q.; Brethouwer, G.; Johansson, A.V.; Henningson, D.S. Simulations of spatially evolving turbulent boundary layers up to Reθ= 4300. Int. J. Heat Fluid Flow 2010, 31, 251–261. [Google Scholar] [CrossRef]

| Itr | Log, | ||||||
|---|---|---|---|---|---|---|---|
| 0 | |||||||
| 5000 | |||||||
| 10,000 | |||||||
| 20,000 | |||||||
| 30,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, F.; Karniadakis, G.E. Variable-Order Fractional Models for Wall-Bounded Turbulent Flows. Entropy 2021, 23, 782. https://doi.org/10.3390/e23060782
Song F, Karniadakis GE. Variable-Order Fractional Models for Wall-Bounded Turbulent Flows. Entropy. 2021; 23(6):782. https://doi.org/10.3390/e23060782
Chicago/Turabian StyleSong, Fangying, and George Em Karniadakis. 2021. "Variable-Order Fractional Models for Wall-Bounded Turbulent Flows" Entropy 23, no. 6: 782. https://doi.org/10.3390/e23060782
APA StyleSong, F., & Karniadakis, G. E. (2021). Variable-Order Fractional Models for Wall-Bounded Turbulent Flows. Entropy, 23(6), 782. https://doi.org/10.3390/e23060782






