Time-Dependent Dephasing and Quantum Transport
Abstract
1. Introduction
2. Characterizing Time-Dependent Non-Markovian Evolutions
3. The Model
4. Time-Dependent Dephasing Assisted Transport
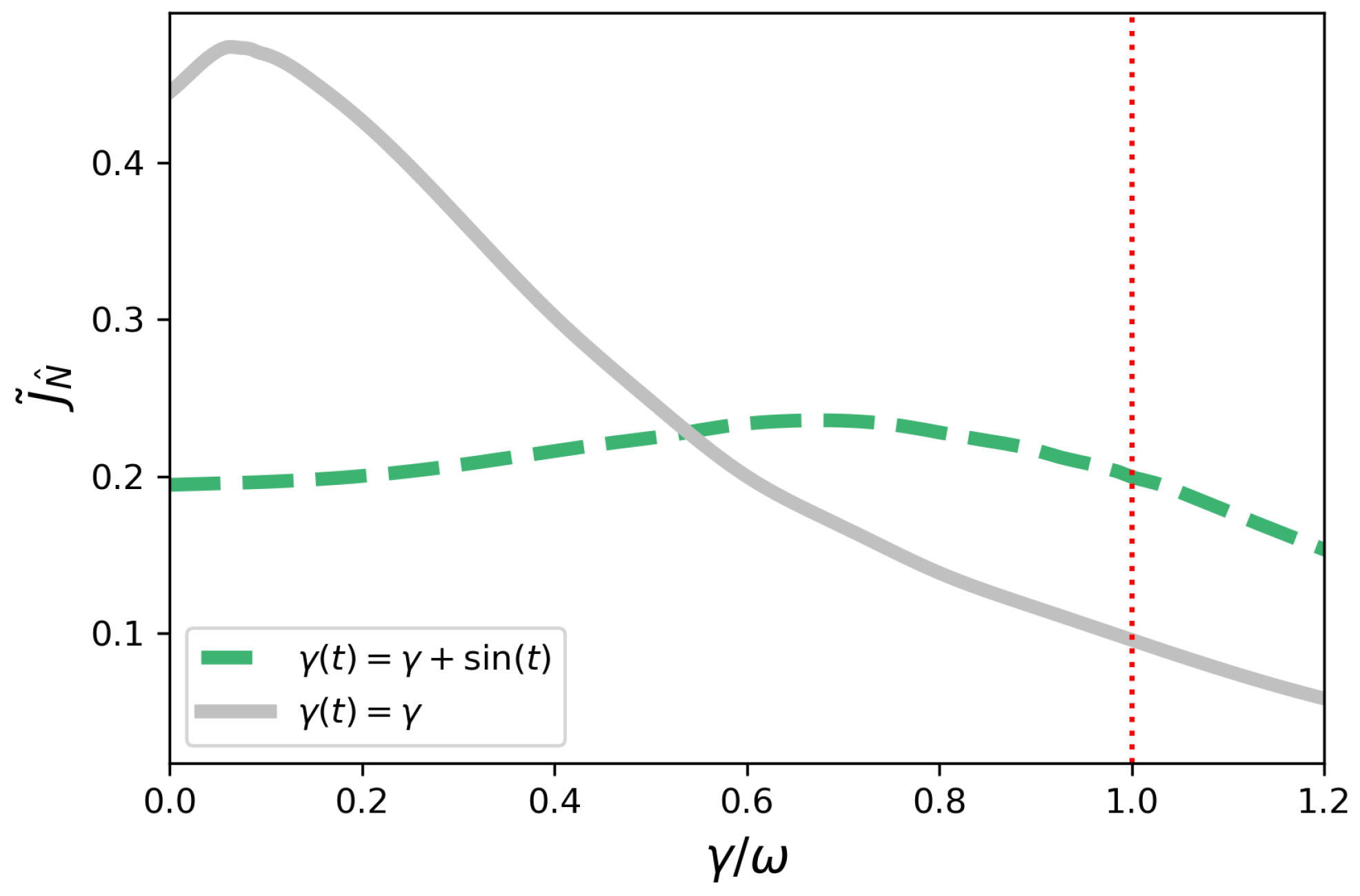
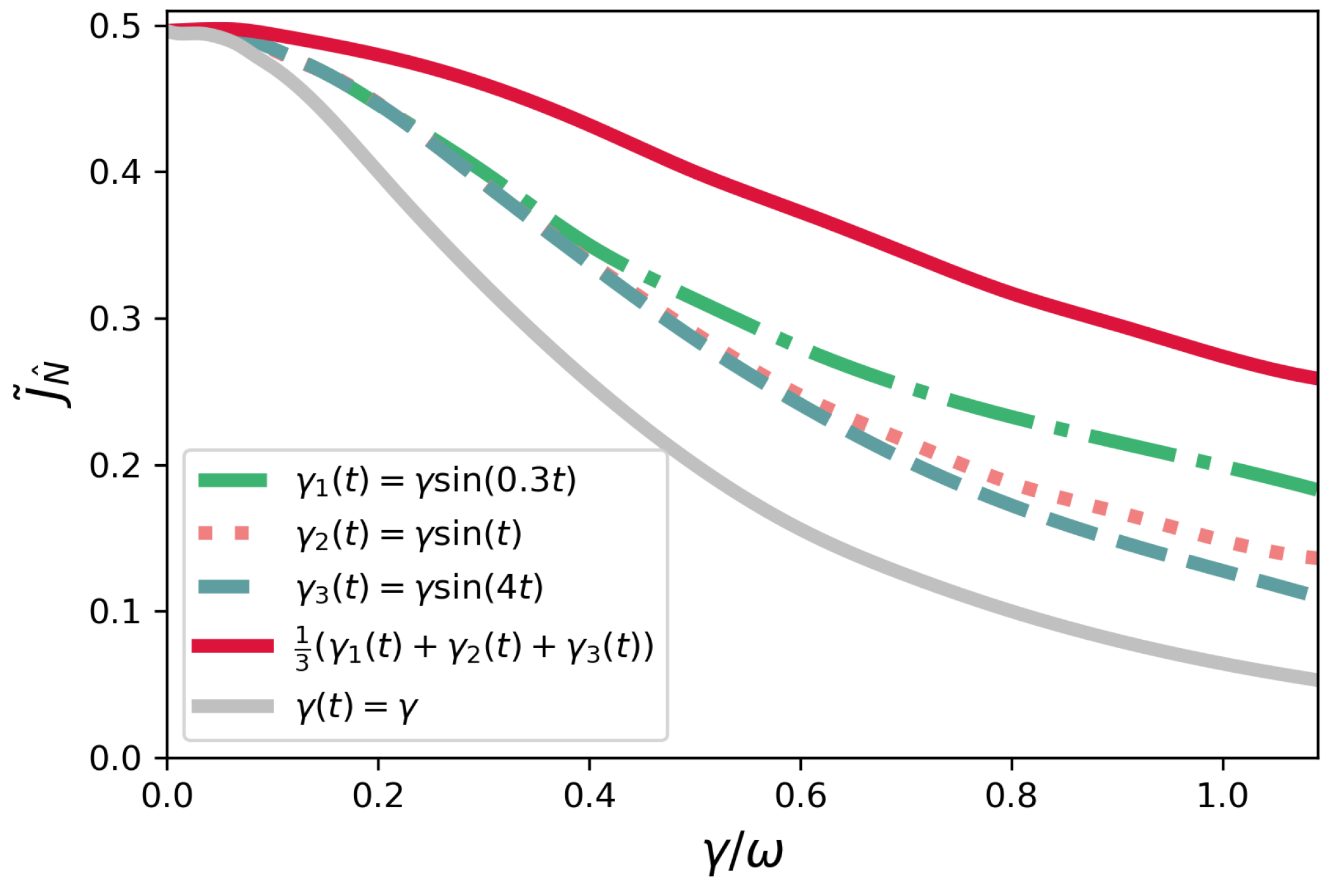
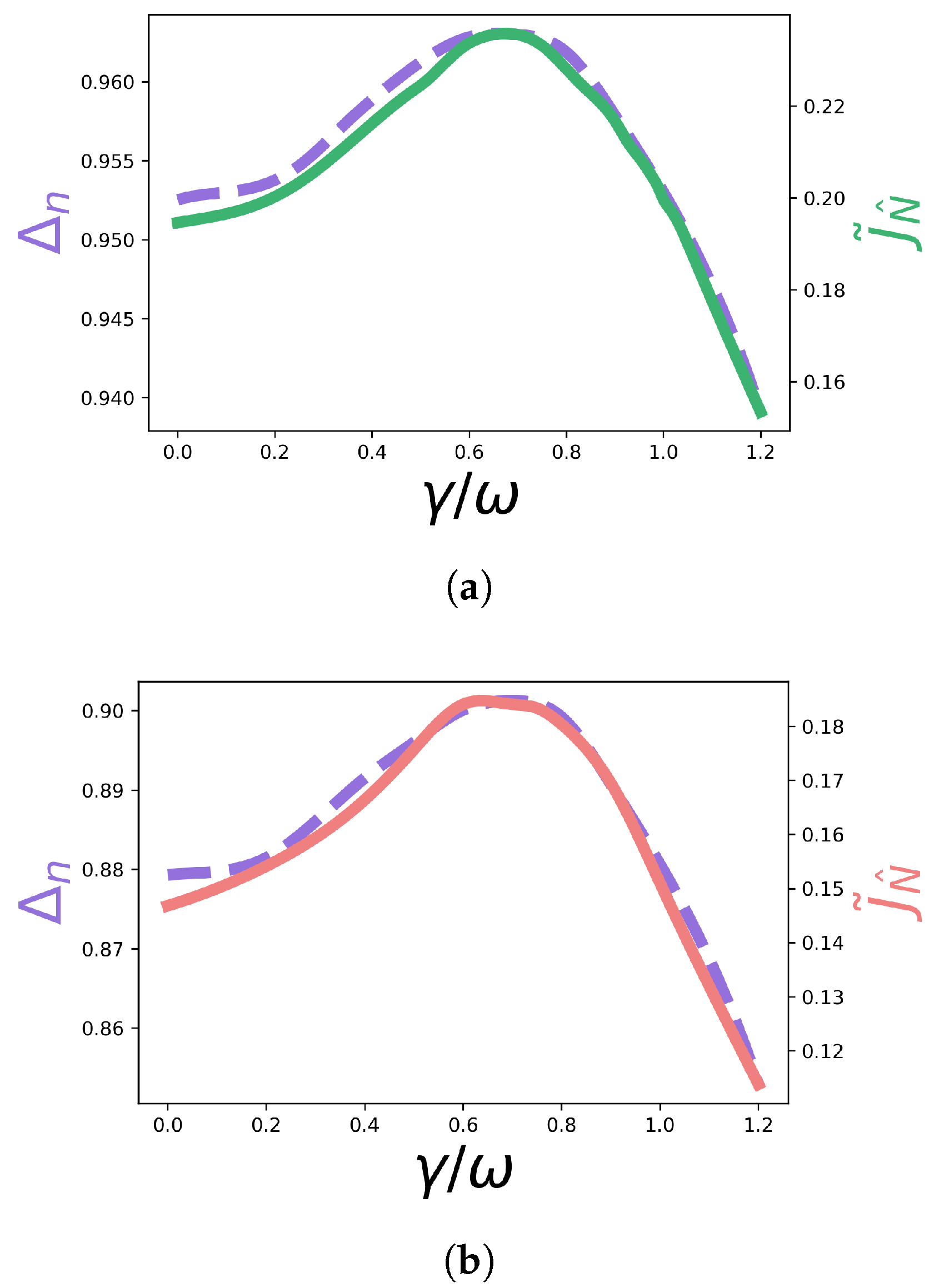
4.1. Non-Symmetric Configuration
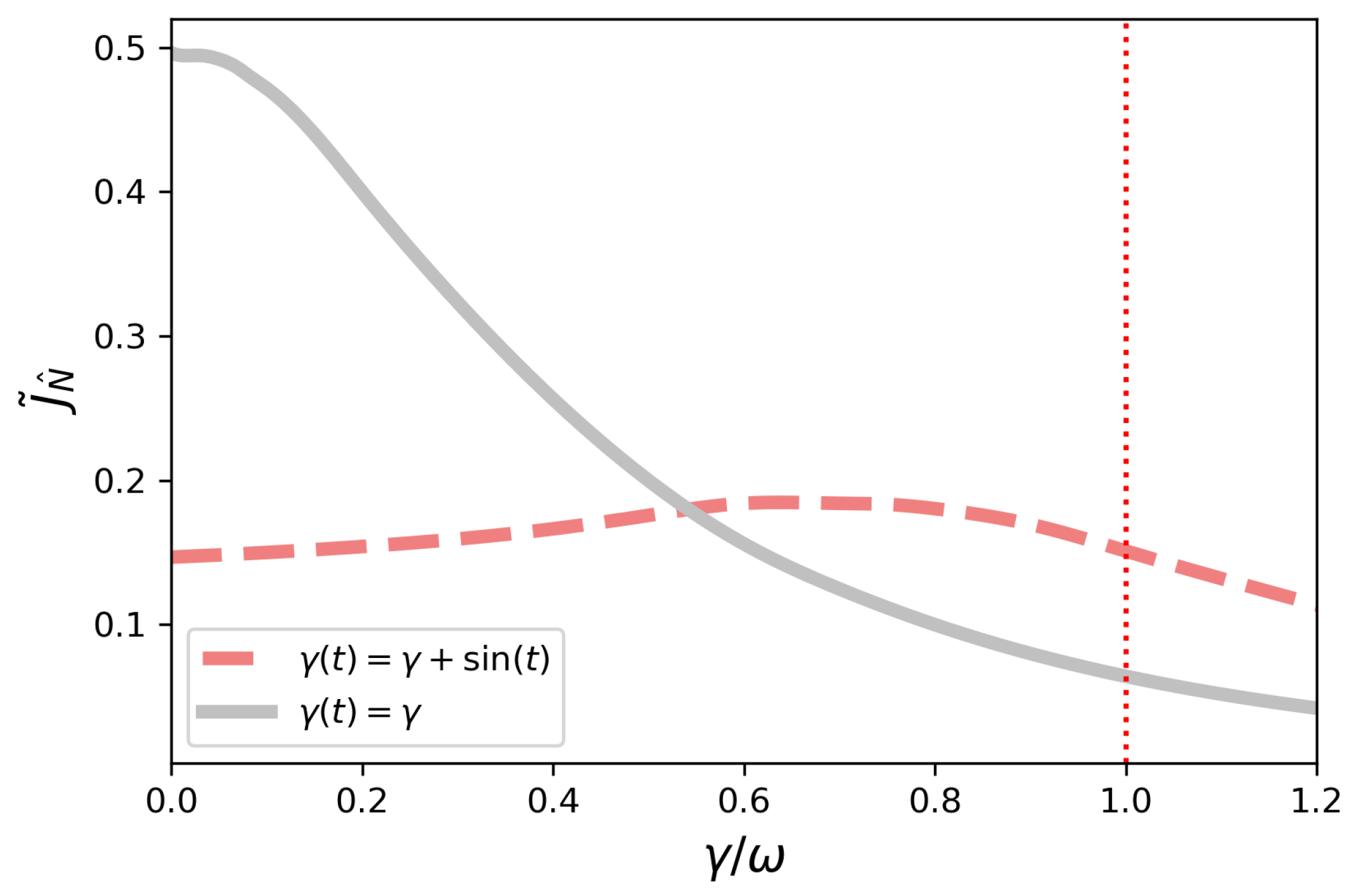
4.2. Symmetric Configuration
4.3. Spread of Occupations and Efficiency
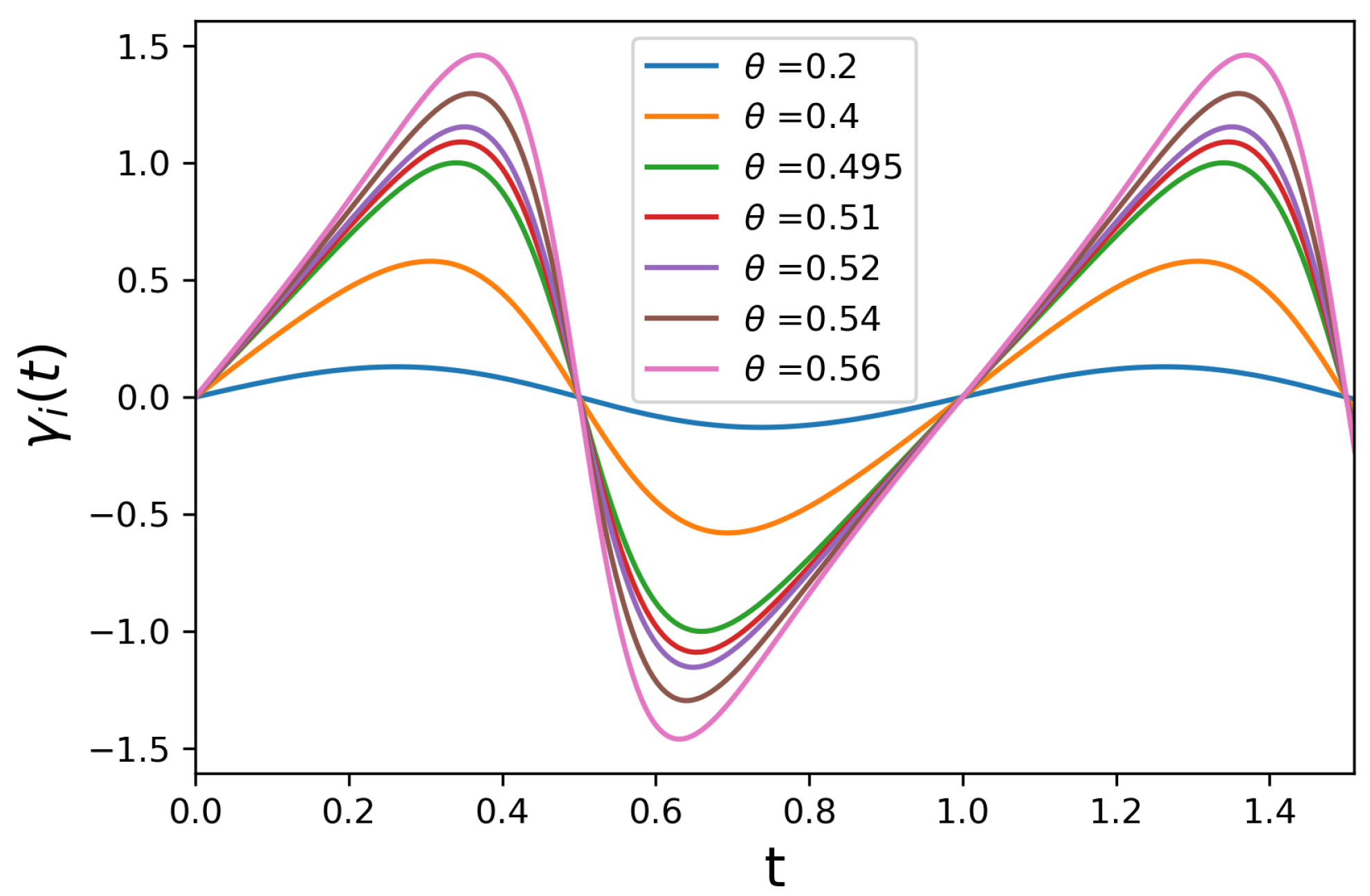
5. Example: Controlled Quantum System
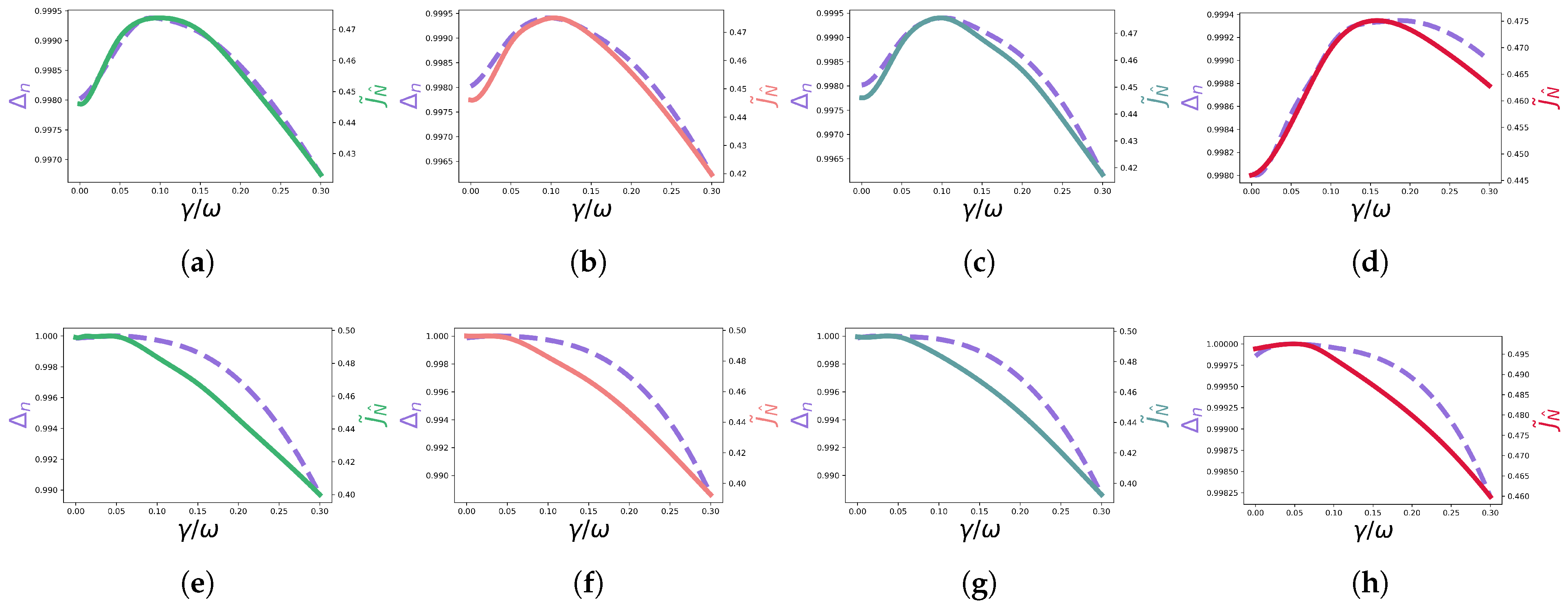
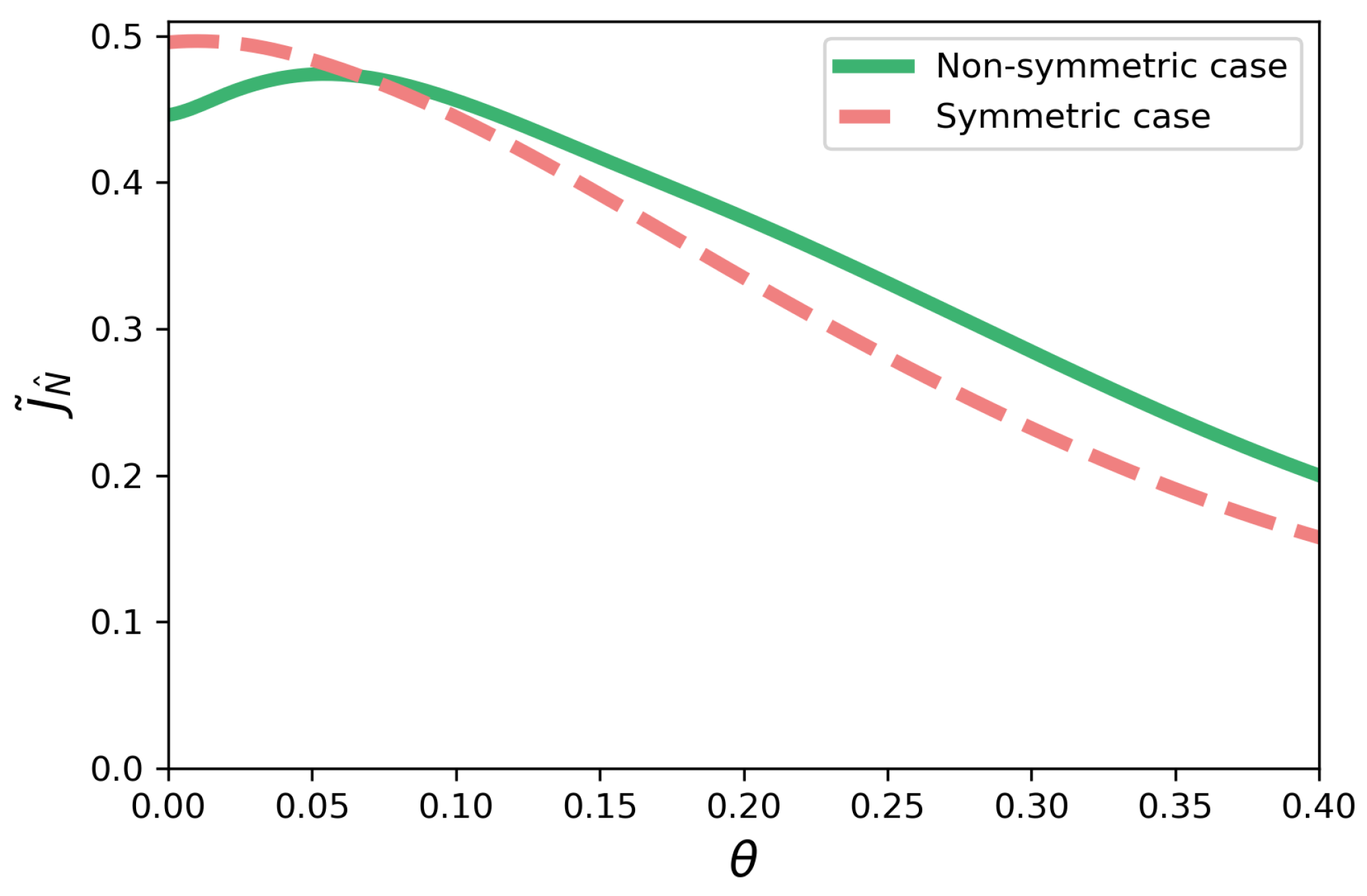
5.1. Non-Symmetric Configuration
5.2. Symmetric Configuration
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Plenio, M.B.; Huelga, S.F. Dephasing-assisted transport: Quantum networks and biomolecules. New J. Phys. 2008, 10, 113019. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Kassal, L.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 2009, 11, 033003. [Google Scholar] [CrossRef]
- Semião, F.L.; Vidiella-Barranco, A. Coherent-state superpositions in cavity quantum electrodynamics with trapped ions. Phys. Rev. A 2005, 71, 065802. [Google Scholar] [CrossRef]
- Engel, G.S.; Calhoun, T.R.; Read, E.L.; Ahn, T.-K.; Mancal, T.; Cheng, Y.-C.; Blankenship, R.E.; Fleming, G.R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782. [Google Scholar] [CrossRef]
- Caruso, F.; Chin, A.W.; Datta, A.; Huelga, S.F.; Plenio, M.B. Highly efficient energy excitation transfer in light-harvesting complexes: The fundamental role of noise-assisted transport. J. Chem. Phys. 2009, 131, 105106. [Google Scholar] [CrossRef]
- Chin, A.W.; Prior, J.; Rosenbach, R.; Caycedo-Soler, F.; Huelga, S.F.; Plenio, M.B. The role of non-equilibrium vibrational structures in electronic coherence and recoherence in pigment-protein complexes. Nat. Phys. 2013, 9, 113. [Google Scholar] [CrossRef]
- Rebentrost, P.; Chakraborty, R.; Aspuru-Guzik, A.J. Non-Markovian quantum jumps in excitonic energy transfer. Chem. Phys. 2009, 131, 184102. [Google Scholar] [CrossRef]
- Moreira, S.V.; Semião, F.L. Investigating nonclassicality in nonlinear electronic spectroscopy. Quantum Sci. Technol. 2019, 4, 03LT01. [Google Scholar] [CrossRef]
- Jang, S.; Hoyer, S.; Fleming, G.; Whaley, K.B. Generalized master equation with non-Markovian multichromophoric Förster resonance energy transfer for modular exciton densities. Phys. Rev. Lett. 2014, 113, 188102. [Google Scholar] [CrossRef] [PubMed]
- Schachenmayer, J.; Genes, C.; Tignone, E.; Pupillo, G. Cavity-Enhanced Transport of Excitons. Phys. Rev. Lett. 2015, 114, 196403. [Google Scholar] [CrossRef]
- Viciani, S.; Gherardini, S.; Lima, M.; Bellini, M.; Caruso, F. Disorder and dephasing as control knobs for light transport in optical fiber cavity networks. Sci. Rep. 2016, 6, 37791. [Google Scholar] [CrossRef]
- Quiroz-Juárez, M.A.; You, C.; Carrillo-Martńez, J.; Montiel-Álvarez, D.; Aragón, J.L.; Magaña-Loaiza, O.S.; de J. León-Montiel, R. Reconfigurable network for quantum transport simulations. Phys. Rev. Res. 2021, 3, 013010. [Google Scholar] [CrossRef]
- Wang, F.; Hou, P.-Y.; Huang, Y.-Y.; Zhang, W.-G.; Ouyang, X.-L.; Wang, X.; Huang, X.-Z.; Zhang, H.-L.; He, L.; Chang, X.-Y.; et al. Observation of entanglement sudden death and rebirth by controlling a solid-state spin bath. Phys. Rev. B 2018, 98, 064306. [Google Scholar] [CrossRef]
- Abrantes, P.P.; Bastos, G.; Szilard, D.; Farina, C.; Rosa, F.S.S. Tuning resonance energy transfer with magneto-optical properties of graphene. Phys. Rev. B 2021, 103, 174421. [Google Scholar] [CrossRef]
- Zerah-Harush, E.; Dubi, Y. Universal Origin for Environment-Assisted Quantum Transport in Exciton Transfer Networks. J. Phys. Chem. Lett. 2018, 9, 1689. [Google Scholar] [CrossRef] [PubMed]
- Semião, F.L.; Furuya, K.; Milburn, G.J. Vibration-enhanced quantum transport. N. J. Phys. 2010, 12, 083033. [Google Scholar] [CrossRef]
- Moreira, S.V.; Marques, B.; Paiva, R.R.; Cruz, L.S.; Soares-Pinto, D.O.; Semião, F.L. Enhancing quantum transport efficiency by tuning non-Markovian dephasing. Phys. Rev. A 2020, 101, 012123. [Google Scholar] [CrossRef]
- Román-Ancheyta, R.; Çakmak, B.; de J. León-Montiel, R.; Perez-Leija, A. Quantum transport in non-Markovian dynamically disordered photonic lattices. Phys. Rev. A 2021, 103, 033520. [Google Scholar] [CrossRef]
- Souza, A.M.; Li, J.; Soares-Pinto, D.O.; Sarthour, R.S.; Oliveira, I.S.; Huelga, S.F.; Paternostro, M.L.; Semião, F. Experimental Demonstration of non-Markovian Dynamics via a Temporal Bell-like Inequality. arXiv 2013, arXiv:1308.5761. [Google Scholar]
- Cárdenas, P.C.; Paternostro, M.; Semião, F.L. Non-Markovian qubit dynamics in a circuit-QED setup. Phys. Rev. A 2015, 91, 022122. [Google Scholar] [CrossRef]
- Brito, F.; Welang, T. A knob for Markovianity. New J. Phys. 2015, 17, 072001. [Google Scholar] [CrossRef]
- Lorenzo, S.; Plastina, F.; Paternostro, M. Tuning non-Markovianity by spin-dynamics control. Phys. Rev. A 2013, 87, 022317. [Google Scholar] [CrossRef]
- Aguado, R.; Brandes, T. Shot Noise Spectrum of Open Dissipative Quantum Two-Level Systems. Phys. Rev. Lett. 2004, 92, 206601. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, P.; Vieira, V.R. Non-Markovian effects in electronic and spin transport. Phys. Rev. B 2015, 92, 100302. [Google Scholar] [CrossRef]
- Zedler, P.; Schaller, G.; Kiesslich, G.; Emary, C.; Brandes, T. Weak coupling approximations in non-Markovian Transport. Phys. Rev. B 2009, 80, 045309. [Google Scholar] [CrossRef]
- Maier, C.; Brydges, T.; Jurcevic, P.; Trautmann, N.; Hempel, C.; Lanyon, B.P.; Hauke, P.; Blatt, R.; Roos, C. Environment-Assisted Quantum Transport in a 10-qubit Network. Phys. Rev. Lett. 2019, 122, 050501. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Laine, E.-M.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Entanglement and Non-Markovianity of Quantum Evolutions. Phys. Rev. Lett. 2010, 105, 050403. [Google Scholar] [CrossRef]
- Hall, M.J.W.; Cresser, J.D.; Li, L.; Andersson, E. Canonical form of master equations and characterization of non-Markovianity. Phys. Rev. A 2014, 89, 042120. [Google Scholar] [CrossRef]
- Breuer, H.-P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Lindblad, G. On the generators of quantum dynamical semigroups. Comm. Math. Phys. 1976, 48, 119. [Google Scholar] [CrossRef]
- Wolf, M.M.; Eisert, J.; Cubitt, T.S.; Cirac, J.I. Assessing Non-Markovian Quantum Dynamics. Phys. Rev. Lett. 2008, 101, 150402. [Google Scholar] [CrossRef]
- Hall, M.J.W. Complete positivity for time-dependent qubit master equations. J. Phys. A 2008, 41, 205302. [Google Scholar] [CrossRef][Green Version]
- Chruscinski, D.; Wudarski, F.A. Non-Markovian random unitary qubit dynamics. Phys. Lett. A 2013, 377, 1425. [Google Scholar] [CrossRef]
- Casparis, L.; Pearson, N.J.; Kringhoj, A.; Larsen, T.W.; Kuemmeth, F.; Nygard, J.; Krogstrup, P.; Petersson, K.D.; Marcus, C.M. Voltage-controlled superconducting quantum bus. Phys. Rev. B 2019, 99, 085434. [Google Scholar] [CrossRef]
- Trautmann, N.; Hauke, P. Trapped-ion quantum simulation of excitation transport: Disordered, noisy, and long-range connected quantum networks. Phys. Rev. A 2018, 97, 023606. [Google Scholar] [CrossRef]
- González, J.O.; Correa, L.A.; Nocerino, G.; Palao, J.P.; Alonso, D.; Adesso, G. Testing the Validity of the ‘Local’ and ‘Global’ GKLS Master Equations on an Exactly Solvable Model. Open Syst. Inf. Dyn. 2017, 24, 1740010. [Google Scholar] [CrossRef]
- Hofer, P.P.; Perarnau-Llobet, M.; Miranda, L.M.; Haack, G.; Silva, R.; Brask, J.B.; Brunner, N. Markovian master equations for quantum thermal machines: Local versus global approach. New J. Phys. 2017, 19, 123037. [Google Scholar] [CrossRef]
- De Chiara, G.; Landi, G.; Hewgill, A.; Reid, B.; Ferraro, A.; Roncaglia, A.J.; Antezza, M. Reconciliation of quantum local master equations with thermodynamics. New J. Phys. 2018, 20, 113024. [Google Scholar] [CrossRef]
- Mitchison, M.T.; Plenio, M.B. Non-additive dissipation in open quantum networks out of equilibrium. New J. Phys. 2018, 20, 033005. [Google Scholar] [CrossRef]
- McConnell, C.; Nazir, A. Electron counting statistics for non-additive environments. J. Chem. Phys. 2019, 151, 054104. [Google Scholar] [CrossRef]
- Santos, J.P.; Semião, F.L. Master equation for dissipative interacting qubits in a common environment. Phys. Rev. A 2014, 89, 022128. [Google Scholar] [CrossRef]
- Liu, Z.D.; Lyyra, H.; Sun, Y.N.; Liu, B.H.; Li, C.F.; Guo, G.C.; Maniscalco, S.; Piilo, J. Experimental implementation of fully controlled dephasing dynamics and synthetic spectral densities. Nat. Commun. 2018, 9, 3453. [Google Scholar] [CrossRef] [PubMed]
- Huelga, S.F.; Plenio, M.B. Vibrations, quanta and biology. Contemp. Phys. 2013, 54, 181. [Google Scholar] [CrossRef]
- Bosman, S.J.; Gely, M.F.; Singh, V.; Bothner, D.; Castellanos-Gomez, A.; Steele, G.A. Approaching ultrastrong coupling in transmon circuit QED using a high-impedance resonator. Phys. Rev. B 2017, 95, 224515. [Google Scholar] [CrossRef]
- Novo, L.; Mohseni, M.; Omar, Y. Disorder-assisted quantum transport in suboptimal decoherence regimes. Sci. Rep. 2016, 6, 18142. [Google Scholar] [CrossRef]
- Zhang, Y.; Celardo, G.L.; Borgonovi, F.; Kaplan, L. Optimal dephasing for ballistic energy transfer in disordered linear chains. Phys. Rev. E 2017, 96, 052103. [Google Scholar] [CrossRef]
- Zerah-Harush, E.; Dubi, Y. Effects of disorder and interactions in environment assisted quantum transport. Phys. Rev. Res. 2020, 2, 023294. [Google Scholar] [CrossRef]
- Budini, A. Maximally non-Markovian quantum dynamics without environment-to-system backflow of information. Phys. Rev. A 2018, 97, 052133. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreira, S.V.; Marques, B.; Semião, F.L. Time-Dependent Dephasing and Quantum Transport. Entropy 2021, 23, 1179. https://doi.org/10.3390/e23091179
Moreira SV, Marques B, Semião FL. Time-Dependent Dephasing and Quantum Transport. Entropy. 2021; 23(9):1179. https://doi.org/10.3390/e23091179
Chicago/Turabian StyleMoreira, Saulo V., Breno Marques, and Fernando L. Semião. 2021. "Time-Dependent Dephasing and Quantum Transport" Entropy 23, no. 9: 1179. https://doi.org/10.3390/e23091179
APA StyleMoreira, S. V., Marques, B., & Semião, F. L. (2021). Time-Dependent Dephasing and Quantum Transport. Entropy, 23(9), 1179. https://doi.org/10.3390/e23091179






