Disentanglement Dynamics in Nonequilibrium Environments
Abstract
:1. Introduction
2. Theoretical Framework
2.1. Non-Markovian Disentanglement Dynamics of a Two-Qubit System
2.2. Relations between Local Decoherence and Nonlocal Entanglement and Quantum Nonlocality
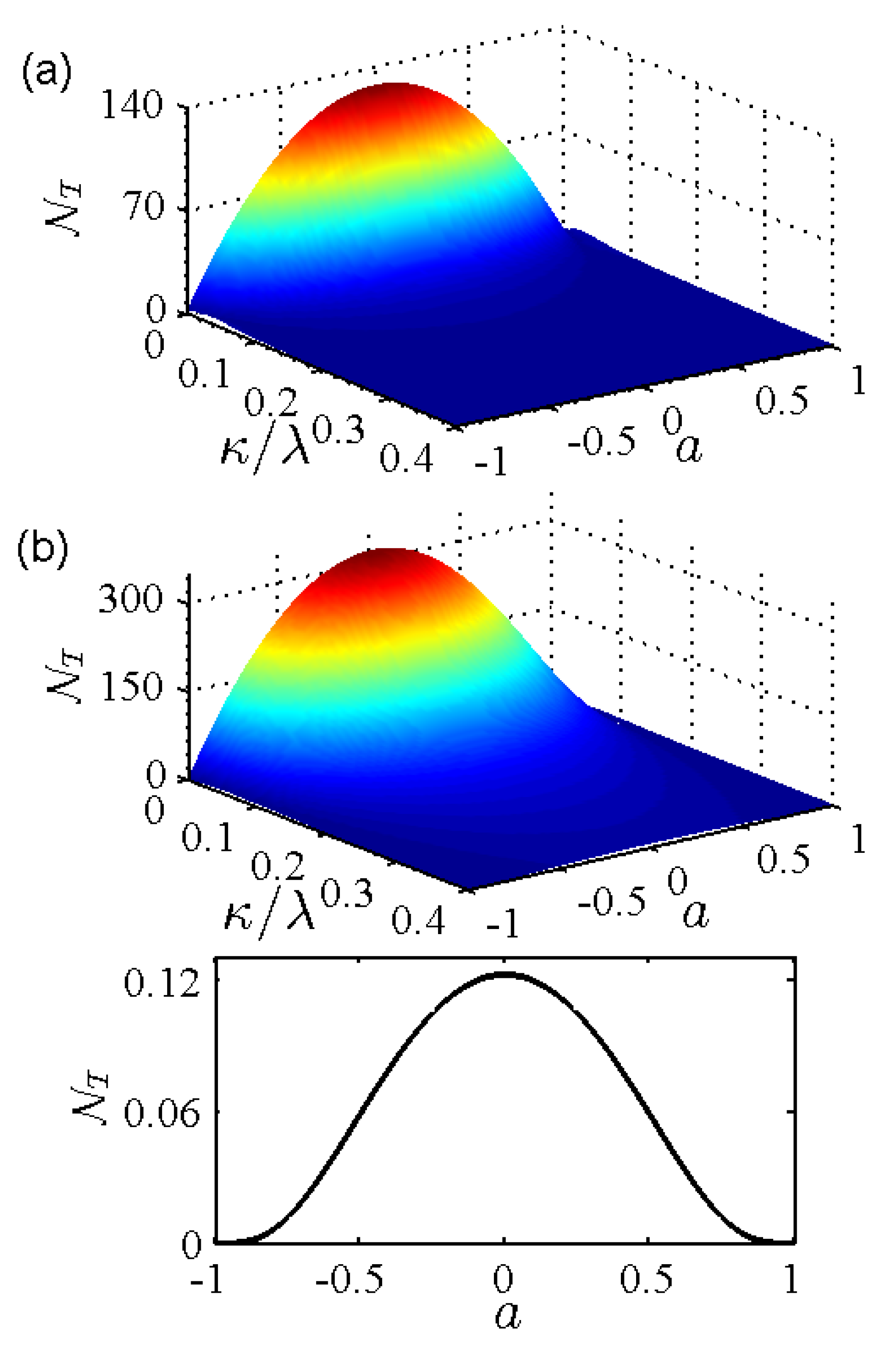
3. Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| RTN | Random telegraph noise |
| CHSH | Clauser-Horne-Shimony-Holt |
| CK | Chapman-Kolmogorov |
Appendix A. Generalized RTN Process Based on Classical Probability Theory
- (1)
- Nonnegative— i.e., ;
- (2)
- Normalization—i.e., ;
- (3)
- Symmetry—i.e., does not change by interchanging arbitrary pairs and ;
- (4)
- Relation between and —i.e., .
Appendix B. Entanglement and Quantum Nonlocality of a Two-Qubit System
References
- Horodecki, R.; Horodecki, P.; Horodecki, M.; Horodecki, K. Quantum entanglement. Rev. Mod. Phys. 2009, 81, 865. [Google Scholar] [CrossRef]
- Chitambar, E.; Hsieh, M.H. Relating the Resource Theories of Entanglement and Quantum Coherence. Phys. Rev. Lett. 2016, 117, 020402. [Google Scholar] [CrossRef] [PubMed]
- Streltsov, A.; Adesso, G.; Plenio, M.B. Colloquium: Quantum coherence as a resource. Rev. Mod. Phys. 2017, 89, 041003. [Google Scholar] [CrossRef]
- Hu, M.L.; Hu, X.; Wang, J.; Peng, Y.; Zhang, Y.R.; Fan, H. Quantum coherence and geometric quantum discord. Phys. Rep. 2018, 762, 1. [Google Scholar] [CrossRef]
- Chitambar, E.; Gour, G. Quantum resource theories. Rev. Mod. Phys. 2019, 91, 025001. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: New York, NY, USA, 2002. [Google Scholar]
- Schlosshauer, M. Decoherence and the Quantum-to-Classical Transition; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Schlosshauer, M. Quantum decoherence. Phys. Rep. 2019, 831, 1. [Google Scholar] [CrossRef]
- Carollo, A.; Valenti, D.; Spagnolo, B. Geometry of quantum phase transitions. Phys. Rep. 2020, 838, 1. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Sudden Death of Entanglement. Science 2009, 323, 598. [Google Scholar] [CrossRef]
- Gurvitz, S.A.; Fedichkin, L.; Mozyrsky, D.; Berman, G.P. Relaxation and the Zeno Effect in Qubit Measurements. Phys. Rev. Lett. 2003, 91, 066801. [Google Scholar] [CrossRef] [PubMed]
- Kang, L.; Zhang, Y.; Xu, X.; Tang, X. Quantum measurement of a double quantum dot coupled to two kinds of environment. Phys. Rev. B 2017, 96, 235417. [Google Scholar] [CrossRef]
- Lan, K.; Du, Q.; Kang, L.; Tang, X.; Jiang, L.; Zhang, Y.; Cai, X. Dynamics of an open double quantum dot system via quantum measurement. Phys. Rev. B 2020, 101, 174302. [Google Scholar] [CrossRef]
- Viotti, L.; Lombardo, F.C.; Villar, P.I. Boundary-induced effect encoded in the corrections to the geometric phase acquired by a bipartite two-level system. Phys. Rev. A 2020, 101, 032337. [Google Scholar] [CrossRef]
- Maniscalco, S.; Francica, F.; Zaffino, R.L.; Lo Gullo, N.; Plastina, F. Protecting Entanglement via the Quantum Zeno Effect. Phys. Rev. Lett. 2008, 100, 090503. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.D.; Bäumer, E.; Tang, J.F.; Hovhannisyan, K.V.; Perarnau-Llobet, M.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Minimizing Backaction through Entangled Measurements. Phys. Rev. Lett. 2020, 125, 210401. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Paraoanu, G.S. Generation and propagation of entanglement in driven coupled-qubit systems. New J. Phys. 2009, 11, 113020. [Google Scholar] [CrossRef]
- Nosrati, F.; Mortezapour, A.; Lo Franco, R. Validating and controlling quantum enhancement against noise by the motion of a qubit. Phys. Rev. A 2020, 101, 012331. [Google Scholar] [CrossRef]
- Nosrati, F.; Castellini, A.; Compagno, G.; Lo Franco, R. Dynamics of spatially indistinguishable particles and quantum entanglement protection. Phys. Rev. A 2020, 102, 062429. [Google Scholar] [CrossRef]
- Czerwinski, A.; Sedziak-Kacprowicz, K.; Kolenderski, P. Phase estimation of time-bin qudits by time-resolved single-photon counting. Phys. Rev. A 2021, 103, 042402. [Google Scholar] [CrossRef]
- Lan, K.; Xie, S.; Cai, X. Geometric quantum speed limits for Markovian dynamics in open quantum systems. New J. Phys. 2022, 24, 055003. [Google Scholar] [CrossRef]
- Collini, E.; Wong, C.Y.; Wilk, K.E.; Curmi, P.M.G.; Brumer, P.; Scholes, G.D. Coherently wired light-harvesting in photosynthetic marine algae at ambient temperature. Nature 2010, 463, 644. [Google Scholar] [CrossRef]
- Panitchayangkoon, G.; Hayes, D.; Fransted, K.A.; Caram, J.R.; Harel, E.; Wen, J.; Blankenship, R.E.; Engel, G.S. Long-lived quantum coherence in photosynthetic complexes at physiological temperature. Proc. Natl. Acad. Sci. USA 2010, 107, 12766. [Google Scholar] [CrossRef] [PubMed]
- Plenio, M.B.; Huelga, S.F. Dephasing-assisted transport: Quantum networks and biomolecules. New J. Phys. 2008, 10, 113019. [Google Scholar] [CrossRef]
- Caruso, F.; Chin, A.W.; Datta, A.; Huelga, S.F.; Plenio, M.B. Highly efficient energy excitation transfer in light-harvesting complexes: The fundamental role of noise-assisted transport. J. Chem. Phys. 2009, 131, 105106. [Google Scholar] [CrossRef]
- Rebentrost, P.; Mohseni, M.; Kassal, I.; Lloyd, S.; Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 2009, 11, 033003. [Google Scholar] [CrossRef]
- Mohseni, M.; Shabani, A.; Lloyd, S.; Omar, Y.; Rabitz, H. Geometrical effects on energy transfer in disordered open quantum systems. J. Chem. Phys. 2013, 138, 204309. [Google Scholar] [CrossRef] [PubMed]
- Piilo, J.; Maniscalco, S.; Härkönen, K.; Suominen, K.A. Non-Markovian Quantum Jumps. Phys. Rev. Lett. 2008, 100, 180402. [Google Scholar] [CrossRef]
- Breuer, H.; Laine, E.; Piilo, J. Measure for the Degree of Non-Markovian Behavior of Quantum Processes in Open Systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Entanglement and Non-Markovianity of Quantum Evolutions. Phys. Rev. Lett. 2010, 105, 050403. [Google Scholar] [CrossRef]
- Zhang, W.M.; Lo, P.Y.; Xiong, H.N.; Tu, M.W.Y.; Nori, F. General Non-Markovian Dynamics of Open Quantum Systems. Phys. Rev. Lett. 2012, 109, 170402. [Google Scholar] [CrossRef]
- Lo Franco, R.; Bellomo, B.; Maniscalco, S.; Compagno, G. Dynamics of quantum correlations in two-qubit systems within non-Markovian environments. Int. J. Mod. Phys. B 2013, 27, 1345053. [Google Scholar] [CrossRef] [Green Version]
- Chruściński, D.; Maniscalco, S. Degree of Non-Markovianity of Quantum Evolution. Phys. Rev. Lett. 2014, 112, 120404. [Google Scholar] [CrossRef] [PubMed]
- Rivas, A.; Huelga, S.F.; Plenio, M.B. Quantum non-Markovianity: Characterization, quantification and detection. Rep. Prog. Phys. 2014, 77, 094001. [Google Scholar] [CrossRef] [PubMed]
- Fanchini, F.F.; Karpat, G.; Çakmak, B.; Castelano, L.K.; Aguilar, G.H.; Farías, O.J.; Walborn, S.P.; Ribeiro, P.H.S.; de Oliveira, M.C. Non-Markovianity through Accessible Information. Phys. Rev. Lett. 2014, 112, 210402. [Google Scholar] [CrossRef]
- Breuer, H.; Laine, E.; Piilo, J.; Vacchini, B. Colloquium: Non-Markovian dynamics in open quantum systems. Rev. Mod. Phys. 2016, 88, 021002. [Google Scholar] [CrossRef]
- de Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Wang, B.; Xu, Z.Y.; Chen, Z.Q.; Feng, M. Non-Markovian effect on the quantum discord. Phys. Rev. A 2010, 81, 014101. [Google Scholar] [CrossRef]
- Bellomo, B.; Lo Franco, R.; Compagno, G. Non-Markovian Effects on the Dynamics of Entanglement. Phys. Rev. Lett. 2007, 99, 160502. [Google Scholar] [CrossRef]
- Chenu, A.; Beau, M.; Cao, J.; del Campo, A. Quantum Simulation of Generic Many-Body Open System Dynamics Using Classical Noise. Phys. Rev. Lett. 2017, 118, 140403. [Google Scholar] [CrossRef] [PubMed]
- Huelga, S.F.; Rivas, A.; Plenio, M.B. Non-Markovianity-Assisted Steady State Entanglement. Phys. Rev. Lett. 2012, 108, 160402. [Google Scholar] [CrossRef]
- Yan, Y.A.; Shao, J. Equivalence of stochastic formulations and master equations for open systems. Phys. Rev. A 2018, 97, 042126. [Google Scholar] [CrossRef]
- Paladino, E.; Galperin, Y.M.; Falci, G.; Altshuler, B.L. 1/f noise: Implications for solid-state quantum information. Rev. Mod. Phys. 2014, 86, 361. [Google Scholar] [CrossRef]
- Addis, C.; Ciccarello, F.; Cascio, M.; Palma, G.; Maniscalco, S. Dynamical decoupling efficiency versus quantum non-Markovianity. New J. Phys. 2015, 17, 123004. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Villar, P.I. Environmentally induced effects on a bipartite two-level system: Geometric phase and entanglement properties. Phys. Rev. A 2010, 81, 022115. [Google Scholar] [CrossRef]
- Ma, J.; Cao, J. Förster resonance energy transfer, absorption and emission spectra in multichromophoric systems. I. Full cumulant expansions and system-bath entanglement. J. Chem. Phys. 2015, 142, 094106. [Google Scholar] [CrossRef]
- Gu, B.; Franco, I. When can quantum decoherence be mimicked by classical noise? J. Chem. Phys. 2019, 151, 014109. [Google Scholar] [CrossRef] [PubMed]
- Poggi, P.M.; Lombardo, F.C.; Wisniacki, D.A. Driving-induced amplification of non-Markovianity in open quantum systems evolution. Europhys. Lett. 2017, 118, 20005. [Google Scholar] [CrossRef]
- Villar, P.I.; Soba, A. Geometric phase accumulated in a driven quantum system coupled to a structured environment. Phys. Rev. A 2020, 101, 052112. [Google Scholar] [CrossRef]
- Czerwinski, A. Open quantum systems integrable by partial commutativity. Phys. Rev. A 2020, 102, 062423. [Google Scholar] [CrossRef]
- Czerwinski, A. Dynamics of Open Quantum Systems-Markovian Semigroups and Beyond. Symmetry 2022, 14, 1752. [Google Scholar] [CrossRef]
- Megier, N.; Smirne, A.; Campbell, S.; Vacchini, B. Correlations, Information Backflow, and Objectivity in a Class of Pure Dephasing Models. Entropy 2022, 24, 304. [Google Scholar] [CrossRef]
- Budini, A.A. Quantum Non-Markovian Processes Break Conditional Past-Future Independence. Phys. Rev. Lett. 2018, 121, 240401. [Google Scholar] [CrossRef]
- Man, Z.X.; Xia, Y.J.; Lo Franco, R. Validity of the Landauer principle and quantum memory effects via collisional models. Phys. Rev. A 2019, 99, 042106. [Google Scholar] [CrossRef]
- Budini, A.A. Conditional past-future correlation induced by non-Markovian dephasing reservoirs. Phys. Rev. A 2019, 99, 052125. [Google Scholar] [CrossRef]
- Budini, A.A. Quantum Non-Markovian Environment-to-System Backflows of Information: Nonoperational vs. Operational Approaches. Entropy 2022, 24, 649. [Google Scholar] [CrossRef]
- Du, P.L.; Wang, Y.; Xu, R.X.; Zhang, H.D.; Yan, Y. System-bath entanglement theorem with Gaussian environments. J. Chem. Phys. 2020, 152, 034102. [Google Scholar] [CrossRef]
- Cai, X. Quantum Dynamics in a Fluctuating Environment. Entropy 2019, 21, 1040. [Google Scholar] [CrossRef]
- Chiang, K.T.; Zhang, W.M. Non-Markovian decoherence dynamics of strong-coupling hybrid quantum systems: A master equation approach. Phys. Rev. A 2021, 103, 013714. [Google Scholar] [CrossRef]
- Zhang, Q.; Man, Z.X.; Xia, Y.J. Non-Markovianity and the Landauer principle in composite thermal environments. Phys. Rev. A 2021, 103, 032201. [Google Scholar] [CrossRef]
- Villar, P.I.; Soba, A. Enhancement of quantum correlations and a geometric phase for a driven bipartite quantum system in a structured environment. Phys. Rev. A 2021, 103, 032222. [Google Scholar] [CrossRef]
- Huang, Y.W.; Zhang, W.M. Exact master equation for generalized quantum Brownian motion with momentum-dependent system-environment couplings. Phys. Rev. Res. 2022, 4, 033151. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Quantum Open System Theory: Bipartite Aspects. Phys. Rev. Lett. 2006, 97, 140403. [Google Scholar] [CrossRef]
- López, C.E.; Romero, G.; Lastra, F.; Solano, E.; Retamal, J.C. Sudden Birth versus Sudden Death of Entanglement in Multipartite Systems. Phys. Rev. Lett. 2008, 101, 080503. [Google Scholar] [CrossRef]
- Mazzola, L.; Maniscalco, S.; Piilo, J.; Suominen, K.A. Interplay between entanglement and entropy in two-qubit systems. J. Phys. B 2010, 43, 085505. [Google Scholar] [CrossRef]
- Salles, A.; de Melo, F.; Almeida, M.P.; Hor-Meyll, M.; Walborn, S.P.; Souto Ribeiro, P.H.; Davidovich, L. Experimental investigation of the dynamics of entanglement: Sudden death, complementarity, and continuous monitoring of the environment. Phys. Rev. A 2008, 78, 022322. [Google Scholar] [CrossRef]
- Mazzola, L.; Maniscalco, S.; Piilo, J.; Suominen, K.A.; Garraway, B.M. Sudden death and sudden birth of entanglement in common structured reservoirs. Phys. Rev. A 2009, 79, 042302. [Google Scholar] [CrossRef]
- Chruściński, D.; Kossakowski, A. Non-Markovian Quantum Dynamics: Local versus Nonlocal. Phys. Rev. Lett. 2010, 104, 070406. [Google Scholar] [CrossRef]
- Wang, F.; Hou, P.Y.; Huang, Y.Y.; Zhang, W.G.; Ouyang, X.L.; Wang, X.; Huang, X.Z.; Zhang, H.L.; He, L.; Chang, X.Y.; et al. Observation of entanglement sudden death and rebirth by controlling a solid-state spin bath. Phys. Rev. B 2018, 98, 064306. [Google Scholar] [CrossRef]
- Martens, C.C. Communication: Decoherence in a nonequilibrium environment: An analytically solvable model. J. Chem. Phys. 2010, 133, 241101. [Google Scholar] [CrossRef]
- Martens, C.C. Quantum dephasing of a two-state system by a nonequilibrium harmonic oscillator. J. Chem. Phys. 2013, 139, 024109. [Google Scholar] [CrossRef]
- Lombardo, F.C.; Villar, P.I. Nonunitary geometric phases: A qubit coupled to an environment with random noise. Phys. Rev. A 2013, 87, 032338. [Google Scholar] [CrossRef] [Green Version]
- Lombardo, F.C.; Villar, P.I. Correction to the geometric phase by structured environments: The onset of non-Markovian effects. Phys. Rev. A 2015, 91, 042111. [Google Scholar] [CrossRef]
- Zheng, Y.; Brown, F.L.H. Single-Molecule Photon Counting Statistics via Generalized Optical Bloch Equations. Phys. Rev. Lett. 2003, 90, 238305. [Google Scholar] [CrossRef] [PubMed]
- Brokmann, X.; Hermier, J.P.; Messin, G.; Desbiolles, P.; Bouchaud, J.P.; Dahan, M. Statistical Aging and Nonergodicity in the Fluorescence of Single Nanocrystals. Phys. Rev. Lett. 2003, 90, 120601. [Google Scholar] [CrossRef] [PubMed]
- Burkard, G. Non-Markovian qubit dynamics in the presence of 1/f noise. Phys. Rev. B 2009, 79, 125317. [Google Scholar] [CrossRef]
- Rossi, M.A.C.; Paris, M.G.A. Non-Markovian dynamics of single- and two-qubit systems interacting with Gaussian and non-Gaussian fluctuating transverse environments. J. Chem. Phys. 2016, 144, 024113. [Google Scholar] [CrossRef]
- Benedetti, C.; Buscemi, F.; Bordone, P.; Paris, M.G.A. Dynamics of quantum correlations in colored-noise environments. Phys. Rev. A 2013, 87, 052328. [Google Scholar] [CrossRef]
- Benedetti, C.; Paris, M.G.A.; Maniscalco, S. Non-Markovianity of colored noisy channels. Phys. Rev. A 2014, 89, 012114. [Google Scholar] [CrossRef]
- Benedetti, C.; Buscemi, F.; Bordone, P.; Paris, M.G.A. Effects of classical environmental noise on entanglement and quantum discord dynamics. Int. J. Quantum Inf. 2012, 8, 1241005. [Google Scholar] [CrossRef]
- Lo Franco, R.; D’Arrigo, A.; Falci, G.; Compagno, G.; Paladino, E. Entanglement dynamics in superconducting qubits affected by local bistable impurities. Phys. Scr. 2012, T147, 014019. [Google Scholar] [CrossRef]
- Silveri, M.P.; Tuorila, J.A.; Thuneberg, E.V.; Paraoanu, G.S. Quantum systems under frequency modulation. Rep. Prog. Phys. 2017, 80, 056002. [Google Scholar] [CrossRef] [Green Version]
- Cialdi, S.; Rossi, M.A.C.; Benedetti, C.; Vacchini, B.; Tamascelli, D.; Olivares, S.; Paris, M.G.A. All-optical quantum simulator of qubit noisy channels. Appl. Phys. Lett. 2017, 110, 081107. [Google Scholar] [CrossRef]
- Cialdi, S.; Benedetti, C.; Tamascelli, D.; Olivares, S.; Paris, M.G.A.; Vacchini, B. Experimental investigation of the effect of classical noise on quantum non-Markovian dynamics. Phys. Rev. A 2019, 100, 052104. [Google Scholar] [CrossRef]
- Fuliński, A. Non-Markovian noise. Phys. Rev. E 1994, 50, 2668. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Zheng, Y. Non-Markovian decoherence dynamics in nonequilibrium environments. J. Chem. Phys. 2018, 149, 094107. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Zheng, Y. Decoherence induced by non-Markovian noise in a nonequilibrium environment. Phys. Rev. A 2016, 94, 042110. [Google Scholar] [CrossRef]
- Cai, X.; Zheng, Y. Quantum dynamical speedup in a nonequilibrium environment. Phys. Rev. A 2017, 95, 052104. [Google Scholar] [CrossRef]
- Lin, D.; Zou, H.M.; Yang, J. Based-nonequilibrium-environment non-Markovianity, quantum Fisher information and quantum coherence. Phys. Scr. 2019, 95, 015103. [Google Scholar] [CrossRef]
- Cai, X.; Meng, R.; Zhang, Y.; Wang, L. Geometry of quantum evolution in a nonequilibrium environment. Europhys. Lett. 2019, 125, 30007. [Google Scholar] [CrossRef]
- Basit, A.; Ali, H.; Badshah, F.; Yang, X.F.; Ge, G.Q. Controlling sudden transition from classical to quantum decoherence via non-equilibrium environments. New J. Phys. 2020, 22, 033039. [Google Scholar] [CrossRef]
- Basit, A.; Ali, H.; Badshah, F.; Yang, X.F.; Ge, G. Nonequilibrium effects on one-norm geometric correlations and the emergence of a pointer-state basis in the weak- and strong-coupling regimes. Phys. Rev. A 2021, 104, 042417. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Finite-time Disentanglement via Spontaneous Emission. Phys. Rev. Lett. 2004, 93, 140404. [Google Scholar] [CrossRef] [PubMed]
- van Kampen, N.G. Stochastic Process in Physics and Chemistry; North-Holland: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Cai, X. Quantum dephasing induced by non-Markovian random telegraph noise. Sci. Rep. 2020, 10, 88. [Google Scholar] [CrossRef] [PubMed]
- Laine, E.M.; Piilo, J.; Breuer, H.P. Measure for the non-Markovianity of quantum processes. Phys. Rev. A 2010, 81, 062115. [Google Scholar] [CrossRef]
- Addis, C.; Haikka, P.; McEndoo, S.; Macchiavello, C.; Maniscalco, S. Two-qubit non-Markovianity induced by a common environment. Phys. Rev. A 2013, 87, 052109. [Google Scholar] [CrossRef]
- Addis, C.; Bylicka, B.; Chruściński, D.; Maniscalco, S. Comparative study of non-Markovianity measures in exactly solvable one- and two-qubit models. Phys. Rev. A 2014, 90, 052103. [Google Scholar] [CrossRef]
- Lo Franco, R.; D’Arrigo, A.; Falci, G.; Compagno, G.; Paladino, E. Preserving entanglement and nonlocality in solid-state qubits by dynamical decoupling. Phys. Rev. B 2014, 90, 054304. [Google Scholar] [CrossRef]
- Lo Franco, R. Nonlocality threshold for entanglement under general dephasing evolutions: A case study. Quantum Inf. Process. 2016, 15, 2593. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of Formation of an Arbitrary State of Two Qubits. Phys. Rev. Lett. 1998, 80, 2245–2248. [Google Scholar] [CrossRef]
- Horodecki, R.; Horodecki, P.; Horodecki, M. Violating Bell inequality by mixed states spin 1/2: Necessary and sufficient condition. Phys. Lett. A 1995, 200, 340. [Google Scholar] [CrossRef]
- Yu, T.; Eberly, J.H. Evolution from entanglement to decoherence of bipartite mixed “X” states. Quantum Inf. Comput. 2007, 7, 459. [Google Scholar]
- Derkacz, L.; Jakóbczyk, L. Clauser-Horne-Shimony-Holt violation and the entropy-concurrence plane. Phys. Rev. A 2005, 72, 042321. [Google Scholar] [CrossRef] [Green Version]
- Mazzola, L.; Piilo, J.; Maniscalco, S. Sudden Transition between Classical and Quantum Decoherence. Phys. Rev. Lett. 2010, 104, 200401. [Google Scholar] [CrossRef] [PubMed]
- Verstraete, F.; Wolf, M.M. Entanglement versus Bell Violations and Their Behavior under Local Filtering Operations. Phys. Rev. Lett. 2002, 89, 170401. [Google Scholar] [CrossRef] [PubMed] [Green Version]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, M.; Chen, H.; Han, T.; Cai, X. Disentanglement Dynamics in Nonequilibrium Environments. Entropy 2022, 24, 1330. https://doi.org/10.3390/e24101330
Chen M, Chen H, Han T, Cai X. Disentanglement Dynamics in Nonequilibrium Environments. Entropy. 2022; 24(10):1330. https://doi.org/10.3390/e24101330
Chicago/Turabian StyleChen, Mingli, Haonan Chen, Tao Han, and Xiangji Cai. 2022. "Disentanglement Dynamics in Nonequilibrium Environments" Entropy 24, no. 10: 1330. https://doi.org/10.3390/e24101330
APA StyleChen, M., Chen, H., Han, T., & Cai, X. (2022). Disentanglement Dynamics in Nonequilibrium Environments. Entropy, 24(10), 1330. https://doi.org/10.3390/e24101330





